PVDF涂层织物拉伸力学性能试验研究

2017-12-18唐柏鉴周道传

东南大学学报（自然科学版） 2017年6期

关键词：纬向双轴铺层

刘平吴刚唐柏鉴周道传缪玮

(1东南大学土木工程学院, 南京 210096)(2江苏科技大学土木工程与建筑学院, 镇江 212005)(3苏州科技大学土木工程学院, 苏州 215009)

PVDF涂层织物拉伸力学性能试验研究

刘平1,2吴刚1唐柏鉴3周道传2缪玮2

(1东南大学土木工程学院, 南京 210096)(2江苏科技大学土木工程与建筑学院, 镇江 212005)(3苏州科技大学土木工程学院, 苏州 215009)

为获得膜材的本构关系规律,以SH-1050P膜材为试验对象, 采用纱线与拉伸方向夹角α为参数进行单轴拉伸破坏试验;然后进行多比例位移加载下的双轴拉伸试验,得到完整的单、双轴试验结果．假设膜片应变均匀且铺层与纱线无滑移,对单轴下膜片弹性模量与夹角α的关系进行了理论推导，并获得膜材力学参数与方向角α的解析公式．同时,假设膜片在双轴加载下为正交弹性双向材料,求解出不同比例加载下的双轴弹性模量与泊松比．结果表明,单轴下膜片弹性模量可按2%的应变划分为弹性与塑性2个阶段,其值与2倍夹角的正弦成线性关系．而双轴试验情况下,在1∶1等量加载时,双轴弹性模量与单轴相同;在非等量加载时,双向加载力离散越大,双轴弹性模量离散性也越大．

膜材;双轴试验;力学性能;正交各向异性

与一般建筑材料不同,膜材具有非线性、各向异性及黏弹性等特征,而且离散性较大,不容易得出可供工程应用的一般性力学参数[1-2]．膜材的力学特性是膜结构设计分析的基础,一直是国内外学者研究的热点．因此,开展膜材力学性能方面的研究,尤其是其弹性模量与泊松比参数的确定,具有重要的意义．国内外对建筑膜材开展了各类力学试验与分析．Minami等[3]假设膜材处于平面应力状态,通过5种比例的双轴试验,由最小二乘法求解出力学常数．Gosling等[1-2]指出,膜材细观结构中存在经纬纱的卷曲及相互摩擦等作用,膜材不满足正交互补定律,不能用单轴拉伸试验预测膜材双轴拉伸弹性常数．

卫东等[4]测试了PVDF/PES膜材的强度、徐变、弹性模量,并与国外双轴试验数据进行了对比．谢顺利等[5]对厚度增强复合材料进行研究,通过采用Z-pinned复合材料方法分析了膜材的力学特性．蒋晓梅等[6]通过对织物表面涂层的沉积过程进行模拟,来定性分析膜材力学参数的规律．陈建稳等[7]则对膜材的力学特性进行了全面评估,从试验方法到微观力学机理等给出了大量的试验数据并进行了理论推导,并结合正交异性弹性板理论给出了一些计算弹性模量的简化公式．

上述文献主要对膜材的解耦弹性常数进行了计算分析,也有些涉及耦合弹性模量[8-9]．但是均没对经纬向方向的变化与弹性模量的规律进行分析,同时也假定在弹性参数与应力比无关的条件下进行分析．为深入分析膜材力学性能及合理利用计算所得常数,有必要对不同经纬向的弹性模量的计算理论及变化规律开展研究．本文对建筑常用膜材PVDF进行了单轴及双轴试验,得出其力学参数;假定膜材为复合纤维材料,纤维与基质无滑移,对膜材不同角度下的弹性模量进行理论推导并得出了解析公式．理论公式与试验结果符合良好,能够较好地解释试验现象．

1 试验概况

单轴拉伸试验方法与传统的拉伸试验方法相同,而双轴拉伸试验则在上海交通大学临近空间中心拉伸实验室自制的多功能薄膜试验台进行(见图1),加载速度为10 mm/min．试验环境如下:温度为(25±2)℃、湿度为(65±2)%．本次试验采用的膜布为建筑上常用的PVDF材料[10-11],型号为SH-1050P,其出厂标定参数见表1．测定此类膜材的弹性模量时,试验应力控制在实际工况的应力范围内,因此经、纬向最大拉力设定为30 kN．

图1 双轴拉伸试验机械

基布类型纱线强度/(N·dtex-1)经纬纱线密度/(yarn·cm-1)基布克重/(g·m-3)总密度/(g·m-3)经纬拉伸强度/(N·(5cm)-1)经纬撕裂强度/N剥离强度/(N·cm-1)高强涤纶丝110012,1227010504200,4500550,500>120/5

单向试件为长带型,宽度B=50 mm,膜带中间自由有效长度L0=200 mm,厚度0.6 mm．膜材长度L0方向的(见图2(a))称为经向(0°)，与长度方向垂直的宽度B方向称为纬向(90°)．本次试验在0～90°之间每15°取一种试件,共7种试验工况;根据德国膜材测试规范规定,每组试件最少取3个．双向试件为十字形切缝试样,核心区域尺寸为16 cm×16 cm,悬臂长16 cm．试样按照膜材的经纬向对称取样,且试样核心区域的臂宽以及悬臂的臂长均不小于16 cm．沿悬臂方向间隔3.2 cm做均匀切缝处理,试样过渡圆弧半径5～15 mm．夹持长度为10 cm,试件的裁剪应尽量沿着膜材两相邻纱线的中间进行,避免纱线散失．试件示意图如图2(b)所示,其中经纬向应力比为1∶1,1∶2,2∶1;每组试件3个,共9个．

(a) 单轴试样

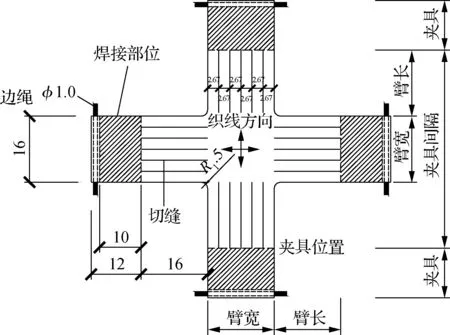
(b) 双轴试样(单位:cm)

2 试验结果

2.1 单轴加载

单轴情况下,分别对绕经向0,15,30,45,60,75,90°七种情况进行试验,以分析拉伸方向与纱线之间夹角对膜材料力学性能的影响．图3分别给出了0,30,60,90°情况下的加载力-位移试验结果．

(a) 0°单轴拉伸试验(b) 30°单轴拉伸试验

从图3可看出,膜材基本上呈现双线性弹性特征．在变形4 mm(应变0.02)内曲线斜率(弹性模量Ee)较大;4 mm之后出现一段较长的塑性段,曲线斜率(塑性模量Ep)较小．单轴情况下试验结果见表2,其中弹性模量及破坏荷载为试验数据的平均值,均方差最大为0.03,说明试验结果离散性较小．

表2 单轴试验结果

2.2 双轴加载

双轴加载情况下,针对典型的经纬向应力比1∶1,1∶2,2∶1三种条件进行了加载试验，试验结果如图4所示．除1∶1应力比外,1∶2,2∶1两种条件下数据波动非常剧烈,表明膜材料的离散性较强．双轴试验应变值是考虑泊松比影响的总应变,要得出单轴情况下的弹性模型,需要将经、纬向数据耦合考虑来求解膜材的力学参数[12-13]．

单轴情况下可以认为其本构关系呈双线性弹性关系．但是这种规律在双轴试验中表现并不明显．通过对数据进行线性拟合分析可看出,均方差值比较小,可以满足工程需要．因此,可以认为此型号膜材为弹性材料．为了简单起见,采用平面内正交各向异性弹性本构模型[14-15]进行分析,各项弹性参数见表3．

表3为双轴试验各项结果不作修正及修正后的数值．不修正计算结果即不考虑泊松比影响的计算结果;修正后数值即考虑了经、纬向数据耦合影响的结果．从修正后结果来看,1∶1应力比情况下与单轴试验结果相接近,其他加载比例下,弹性模量与单轴试验结果相差较大,且应力较大时弹性模量也较大;泊松比结果离散性较弱,平均值在0.11附近．这种较为明显的差异是由于经、纬向纱线与涂层的复杂相互作用引起的．

(a) 纬向1∶1加载(b) 经向1∶1加载

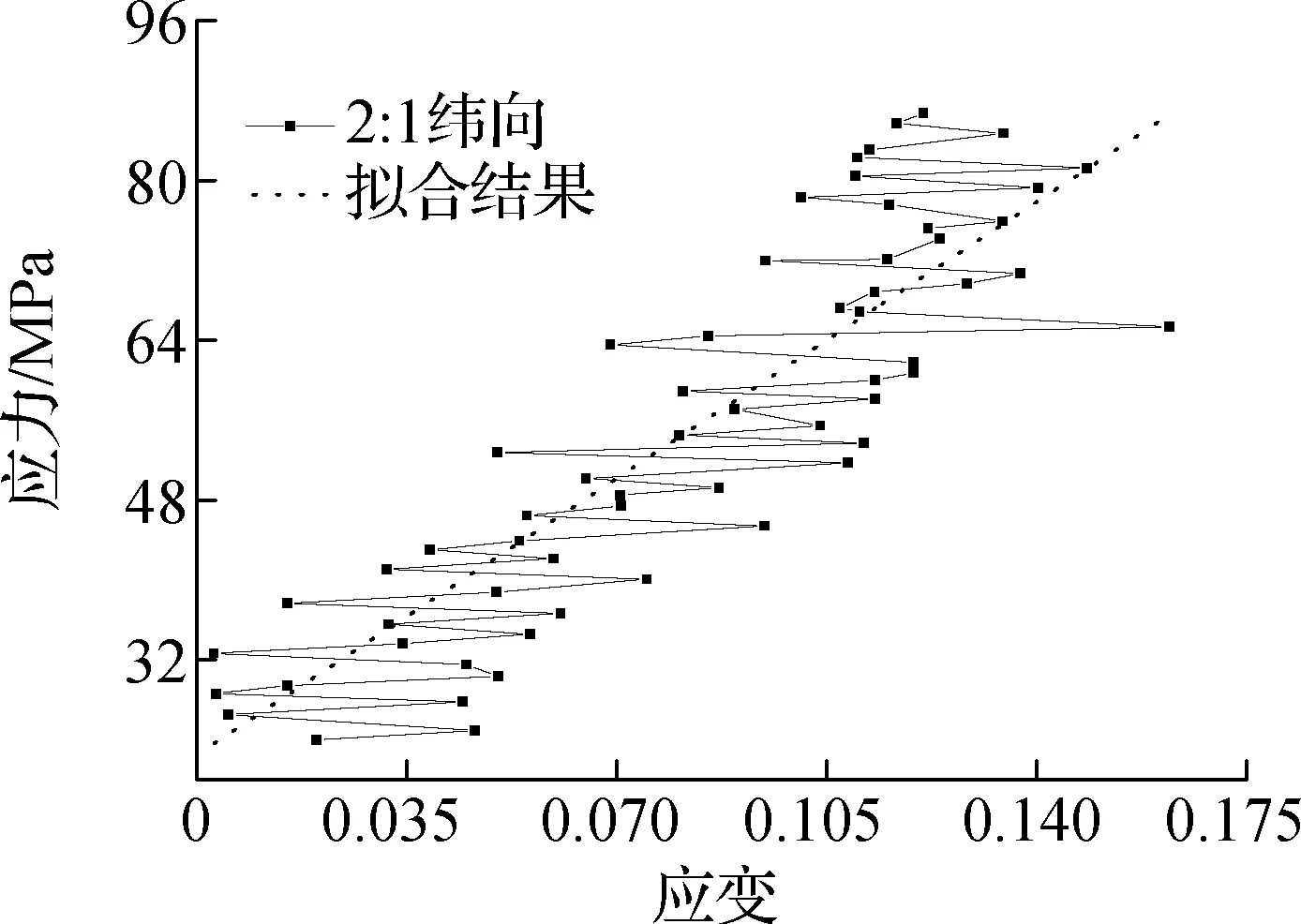
(e) 纬向2∶1加载 (f) 经向2∶1加载

应力比1∶11∶22∶1纬向弹性模量/MPa204/160116/98197/232经向弹性模量/MPa295/183109/88-56/87泊松比无/0.11无/0.09无/0.13

3 理论分析

根据膜片的生产过程可知,膜片单元如图5(a)所示．其中纱线呈正交布置而铺层则覆盖纱线．图5(b)为纱线之间的一片单元受力示意图．假设膜片单元应变均匀且纱线与铺层之间无滑移．设纱线经、纬向在膜片的折合弹性模量为E1,E2;与拉伸方向的夹角分别为θ1,θ2,经、纬向正交,有θ1+θ2=π/2．膜片拉伸向截面面积为A．设膜片在拉伸方向应变为ε,则纱线应变为εs=εcos(θi),其中,i=1,2．

根据膜片结构知,纱线受力为形变产生的应力与铺层对纱线的剪应力之和．形变在拉伸方向产生的拉力为:E1εcos2(θ1)+E2εsin2(θ1)．设经线方向对铺层产生的剪应力为T1,由剪应力互等定理知,铺层纬向方向的剪应力T2=T1(见图5(b))．则剪应力在纱线上拉伸方向产生的力可表示为Esεcos(θ1)sin(θ1),Es为由膜片尺寸、纱线间距、膜片剪切模量决定的常数,并且方向与形变产生的力相反．由经、纬向纱线相互作用知,纱线在拉伸向的合力为

(a) 膜片简化(b) 膜片单元分析

F=E1εcos2(θ1)+E2εsin2(θ1)-
2Esεsin(θ1)cos(θ1)

则纱线在拉伸方向的折合模量为

E′=E1cos2(θ1)+E2sin2(θ1)-Essin(2θ1)

(1)

本文选取的膜材经、纬向纱线分布相同,因此E1=E2,夹角为α．式(1)可简化为

E′=E1-Essin(2α)

再加上铺层的弹性模量,则膜材在拉伸方向的模量为

E=Eb-Essin(2α)

(2)

式中,Eb为铺层模量与纱线折合模量之和;Es需要试验确定．从式(2)可看出,弹性模量与2α成正弦关系,α=45°时弹性模量最小．在双轴拉伸时,由于1∶1经、纬向应变相等,应变夹角为45°,因此试验结果最均匀,没有波动;而当经、纬向拉伸为其他比例时,角度不断变化,因此试验结果波动较大(见图4)．此外,由于本文膜材铺层模量与纱线模量未知,因此Eb,Es均需要试验确定;而且由于纱线模量大、屈服应变小,因此其在试验中首先屈服,而此时铺层仍处于弹性段,所以膜材呈两段线性关系．方便起见,本文仍称第二阶段为塑性段．

根据式(2),试验结果采用最小二乘法回归分析,可得

Ee=158+139sin(2α),Ep=74+56sin(2α)

曲线对于45°成对称分布．回归结果与试验结果对比见图6,由图可见,理论预测规律与试验结果符合良好．但60°试验结果中Ee误差较大,根据已知的纺织理论,可以认为:虽然纱线正交且材质、经纬向单位数量相同,但是由于膜材成型时,先在经向纱线拉直再穿织纬向纱线,因此膜材在2个方向变形时,经、纬向纱线的相互影响并不相等(与纺织工艺有关)．一般而言,经向纱线对纬向纱线作用力较强,而纬向纱线对于经向纱线作用力较弱．因此在60°时,纬向纱线变形为主,相互作用力较弱．而在进行理论分析时并没有考虑这种差异,因此产生了较大误差．

(a) 弹性模量

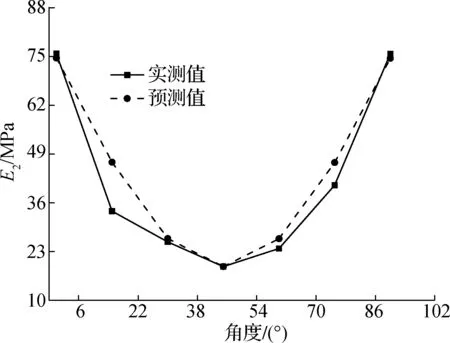
(b) 塑性模量

4 结论

1) 在单轴荷载作用下可认为膜材符合双线性弹性模型,其中弹性段应变区间为0～0.02．

2) 双向应力情况下,膜材可看作正交各向异性弹性材料．膜材的弹性模量与应力比相关，而泊松比与应力比无关;双向应力相同(应力比1∶1)的情况下,其弹性模量与单轴一致．

3) 推导出膜材单向拉伸下弹性模量与铺层及纱线的折合模量成正比,与2倍夹角的正弦成正比,理论公式为E=Eb-Essin(2α)．

致谢本文实验均在上海交通大学临近空间结构中心陈务军教授实验室完成．对于陈务军教授、高成军博士的指导与帮助,在此表示真诚感谢．

)

[1] Gosling P D, Bridgens B N, Zhang L. Adoption of a reliability approach for membrane structure analysis[J].StructuralSafety, 2012,40: 39-50. DOI:10.1016/j.strusafe.2012.09.002.

[2] Gosling P D, Bridgens B N, Albrecht A, et al. Analysis and design of membrane structures: Results of a round robin exercise[J].EngineeringStructures, 2013,48: 313-328. DOI:10.1016/j.engstruct.2012.10.008.

[3] Minami H, Motobayashi S. Biaxial deformation property of coated plain-weave fabrics[C]//ProceedingsofSymposiumonArchitecturalFabricStructures. Orlando, USA,1984:1782-1789.

[4] 卫东, 杨庆山, 沈世钊. 张拉膜结构模型全过程试验研究[J]. 建筑结构学报, 2004, 25(2): 49-56,78. DOI:10.3321/j.issn:1000-6869.2004.02.009.

Wei Dong, Yang Qingshan, Shen Shizhao. Study on full process experiment of full-scale tensioned membrane structure[J].JournalofBuildingStructures, 2004,25(2): 49-56,78. DOI:10.3321/j.issn:1000-6869.2004.02.009.(in Chinese)

[5] 谢顺利, 张彩丽, 张春丽, 等. 厚度增强复合材料研究现状及进展[J]. 硅酸盐通报, 2016, 35(2): 464-467,473.

Xie Shunli, Zhang Caili, Zhang Chunli, et al. Development of composite laminates with through-thickness-reinforcements[J].BulletinoftheChineseCeramicSociety, 2016,35(2): 464-467,473.(in Chinese)

[6] 蒋晓梅, 陈国强, 芮延年. 织物表面涂层沉积过程模拟[J]. 纺织学报, 2015, 36(1): 72-76. DOI:10.13475/j.fzxb.20140102805.

Jiang Xiaomei, Chen Guoqiang, Rui Yannian. Simulation of coating deposition process on fabric surface[J].JournalofTextileResearch, 2015,36(1): 72-76. DOI:10.13475/j.fzxb.20140102805.(in Chinese)

[7] 陈建稳, 陈务军, 赵兵. 浮空器膜材循环拉伸力学性能及弹性常数研究[J]. 湖南大学学报(自然科学版), 2013, 40(6): 40-46. DOI:10.3969/j.issn.1674-2974.2013.06.007.

Chen Jianwen, Chen Wujun, Zhao Bing. Study of the mechanical properties and elastic constants of aerostat envelope fabric under cyclic tensile loading[J].JournalofHunanUniversity(NaturalSciences), 2013,40(6): 40-46. DOI:10.3969/j.issn.1674-2974.2013.06.007.(in Chinese)

[8] Sun X Y, Chen Z Q, Wu Y, et al Numerical studies on the behaviors of wind-structure interaction for membrane structures[C]//TheSeventhInternationalColloquiumonBluffBodyAerodynamicsandApplications. Shanghai, China, 2012:765-772.

[9] Yang Q S, Wu Y, Zhu W L. Experimental study on interaction between membrane structures and wind environment[J].EarthquakeEngineeringandEngineeringVibration, 2010,9(4):523-532.

[10] 李大鹏. 建筑用纺织材料的应用[J]. 现代装饰(理论), 2016,43(6):250.

Li Dapeng. Application research progress of textile material used in construction field[J].CottonTextileTechnology, 2016,43(6):250.

[11] 王茜. 用材料去思维——浅谈膜结构[J]. 艺术品鉴, 2015(6): 310+309.

[12] Drioli E, Ali A, Macedonio F. Membrane distillation: Recent developments and perspectives[J].Desalination, 2015,356: 56-84. DOI:10.1016/j.desal.2014.10.028.

[13] Zhan M L, Zhang W J, Sheng J C, et al. Membrane finite element method for simulating fluid flow in porous medium[J].WaterScienceandEngineering, 2009,2(2):43-51.

[14] Zhang Q L, Wu H G. Using softened contact relationship describing compressible membrane in FEA of spiral case structure[J].ArchivesofCivilandMechanicalEngineering, 2013,13(4): 506-517. DOI:10.1016/j.acme.2013.04.009.

[15] Guo J, Zheng Z, Wu S. An impact vibration experimental research on the pretension rectangular membrane structure[J].AdvancesinMaterialsScienceandEngineering, 2015,2015: 1-8. DOI:10.1155/2015/387153.

ExperimentalstudyonmechanicalpropertiesofPVDFtextile

Liu Ping1,2Wu Gang1Tang Baijian3Zhou Daochuan2Miao Wei2

(1School of Civil Engineering, Southeast University,Nanjing 210096, China) (2School of Civil Engineering and Architecture, Jiangsu University of Science and Technology,Zhenjiang 212005, China) (3School of Civil Engineering, Suzhou University of Science and Technology, Suzhou 215009, China)

To obtain the constitutive model of membrane, the uniaxial tensile failure experiments of SH-1050P textile were carried out using the angle of yarn and tensile direction as the parameters. Besides, the biaxial tensile test under biaxial loading with multiple loading ratio was also conducted to obtain the complete uniaxial/biaxial test data. The analytical formula about the relationship between the elastic modulus and the angle was derived based on the assumption that the strains of all the membranes are uniform and there is no slippage between ply and yarn, which can explain the experimental phenomena well. Meanwhile, the biaxial elastic modulus and Poisson’s ratio under different proportional loading were obtained with the assumption of the membrane being a biaxial orthogonal elastic model under biaxial loading. The results show that the elastic modulus of the uniaxial test can be divided into the elasticity and plasticity stages according to the ultimate elastic strain of 2%. Both two elastic modulus values are proportional to 2 times of angle. As for the bi-axial test, the elastic modulus is the same as that of the uniaxial test when the loading ratio is 1∶1, and the discreteness of elastic modulus increases with the discreteness of the loading ratio.

membrane; bi-axial test; mechanical property; orthotropic

10.3969/j.issn.1001-0505.2017.06.018

TU599

1001-0505(2017)06-1195-06

2017-04-10.

刘平(1983—)，男，博士，讲师，liupinghaiyan@163.com.

国家自然科学基金资助项目(51508238)、江苏省博士后科研基金资助项目(1601014B).

刘平,吴刚,唐柏鉴,等.PVDF涂层织物拉伸力学性能试验研究[J].东南大学学报(自然科学版),2017,47(6):1195-1200.

10.3969/j.issn.1001-0505.2017.06.018.