铅芯橡胶支座单元模型的开发及验证

周 通 李爱群,2,3

(1东南大学土木工程学院, 南京 210096)(2北京未来城市设计高精尖创新中心, 北京 100044)(3北京建筑大学土木与交通工程学院, 北京 100044)

铅芯橡胶支座单元模型的开发及验证

周 通1李爱群1,2,3

(1东南大学土木工程学院, 南京 210096)(2北京未来城市设计高精尖创新中心, 北京 100044)(3北京建筑大学土木与交通工程学院, 北京 100044)

为了提高铅芯橡胶支座力学性能计算分析的准确性和效率,基于OpenSees有限元程序开发了相应的单元模型,综合考虑了支座双向耦合行为和圆形截面各向同性的特点,并计入压缩刚度、临界承载力随侧移的变化效应以及加载历程对于支座拉伸方向累积损伤、强度退化等性能的影响.为验证单元模型的有效性,分别针对水平双向位移控制试验、静力循环拉伸试验及隔震桥梁动力试验进行了模拟分析.结果表明,所提模型能够较为合理地模拟支座的力学特性,在单元内部考虑支座力学性能的变化效应可以较为准确地反映其在地震动作用下的响应表现,为进一步开展隔震结构地震响应分析奠定基础.

铅芯橡胶支座;水平双向耦合;竖向压缩刚度;验证

隔震技术易于实施,且减震控制效果优良,被越来越多地应用于新建结构及既有建筑的加固改造中.基础隔震通过增加隔震系统的水平柔度来分离上部结构与水平向地震动,并提供适当的阻尼以消耗地震能量.铅芯橡胶支座是目前应用最为广泛的隔震装置,其力学性能有待进一步深入研究.Warn等[1]试验研究了侧移对于支座压缩刚度的影响,并对比分析了重叠面积法、拉伸屈曲公式、双弹簧模型及分段线性法的准确性,指出分段线性公式与试验结果最为吻合.Vemuru等[2]通过静、动力试验分析了侧移状态下支座的失稳破坏模式,指出采用重叠面积法计算支座侧移状态下的临界承载力过于保守,且铅芯对于支座稳定性能的影响较小. Koh等[3]提出了一种考虑支座水平与竖向间耦合作用的双弹簧模型,涉及侧移对竖向刚度的影响以及水平刚度随竖向压力的变化效应. Vemuru等[4]针对动力荷载作用下隔震支座水平与竖向间耦合效应,提出了相应的支座模型,但仅依靠静力试验并不能确定该模型中的参数.Maureira等[5]基于单层橡胶的力学方程,通过CR列式转换,推导得到支座整体的力学公式,该模型既可以反映支座的整体性能,又能表征各橡胶层的力学行为.

本文基于OpenSees有限元程序[6]开发了铅芯橡胶支座单元模型,该模型综合考虑了支座的水平双向耦合行为、压缩刚度和临界承载力随侧移的变化效应以及非线性拉伸性能等特性.为验证单元模型的有效性,针对相应的静、动力试验结果进行模拟分析,并研究了考虑力学特性的变化效应对于支座性能表现的影响.

1 隔震支座单元模型

1.1 水平向剪切性能

铅芯橡胶支座在水平向表现出非线性滞回行为.Park等[7]基于单向Bouc-Wen模型提出了双向Park模型,考虑了支座在水平面内的双向耦合效应,目前已被广泛应用于SAP2000等程序中.然而,该模型在2个正交方向上的加卸载规则不一致,违背了圆形截面支座各向同性的假定.文献[8]针对2个正交方向上的加卸载判别条件进行改进,提出了Casciati模型,使其符合假定的要求.本文采用Casciati模型来考虑支座的水平双向耦合效应.

在Casciati模型中,x,y向恢复力Fx和Fy满足如下关系:

(1)

式中,Kd为支座屈服后刚度;Ux和Uy分别为支座x,y方向上的变形量;Qd为支座的特征强度;cb为橡胶材料的黏滞阻尼,通常忽略不计;Z={Zx,Zy}T为支座的滞回位移矢量(无量纲),作为Ux和Uy的函数,满足如下一阶非线性微分方程:

(2)

式中

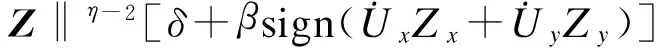
(3)

式中,Y=Qd/((τ-1)Kd)为支座的屈服位移,其中,参数τ为屈服前、后刚度比值,通常取值为10;参数η控制着恢复力曲线由弹性到塑性过渡的光滑程度;I为二阶单位矩阵;参数δ,β和A共同决定着恢复力-位移关系的形状和大小;滞回位移矢量的大小‖Z‖由下式决定:

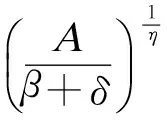
(4)

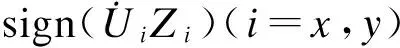
基于双弹簧模型来考虑竖向压力对支座水平刚度的影响[9],其表达式为

(5)

式中,G为橡胶的剪切模量;Ab为支座的截面面积;Tr为支座内橡胶层的总厚度,且Tr=ntr,其中,n为橡胶层数,tr为单层橡胶厚度;P为竖向压力;Pcr,0为支座的初始临界承载力.

1.2 轴向性能

支座具有较小的水平刚度,在地震动作用下隔震层通常会产生较大的水平位移,支座的竖向刚度和临界承载力随之降低.在竖向地震动分量及上部结构倾覆力矩的联合作用下,支座可能产生拉伸变形.所提单元模型综合考虑了以上因素的影响,从而更加准确地描述了支座的力学性能.

1.2.1 压缩性能

当支座截面的内外半径分别为r和R时,初始压缩刚度为

(6)

式中,Ec为橡胶的压缩模量,且[9]

(7)

式中

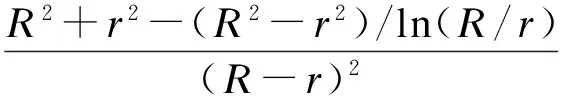
(8)

式中,S1=R/(2tr)为第一形状系数;K为橡胶体积弹性模量,通常取2 GPa.

采用已被试验验证的分段线性公式来考虑水平位移uh对支座竖向刚度Kv的影响,其表达式如下[1]:

(9)

为有效判别支座的失稳破坏模式,准确计算竖向临界承载力显得尤为重要.基于Haringx理论,支座的初始临界荷载Pcr,0为[10]

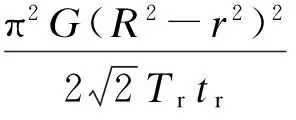
(10)

由于重叠面积法过于保守地考虑侧移对于支座临界承载力降低程度的影响,本文采用下式计算支座在侧移状态下的临界承载力Pcr[11]:

(11)

式中,γ=uh/Tr为水平剪应变;S2=2R/Tr为第二形状系数.

1.2.2 拉伸性能

现有程序中常常忽略支座的拉伸性能或者采用线弹簧模型来模拟支座的拉伸力学行为.本文采用Kumar[12]提出的拉伸模型来合理地考虑支座的拉伸性能.如图1所示,支座进入拉伸状态后,在拉伸荷载达到初始损伤强度(Fc=3GAb)前,处于线弹性阶段,且拉伸刚度与压缩刚度一致.此后,当拉伸荷载超过Fc时,拉伸承载力按下式计算:

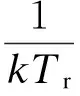
(12)

式中,uv为当前拉伸位移值;uc为初始损伤强度Fc所对应的拉伸变形值,且uc=Fc/Kv;参数k用于反映支座的拉伸损伤程度,k值越大,支座损伤后承载力降低程度越大.

当拉伸位移超过uc并随后卸载时,卸载路径不同于原先加载路径.再次加载时,首先沿着先前卸载路径直至拉伸位移值uv超过已经历的最大位移umax(见图1),当荷载进一步增加时,后续过程遵循式(12).再次卸载时,重新形成新的卸载路径.每个循环的卸载路径均近似沿着(umax,Fmax)与(ucn,Fcn)两点间的直线,且两者均随着加载过程的进行而不断变化.其中,Fcn为当前损伤强度,其降低程度取决于当前已经历的最大变形值umax,即

(13)

式中,α为强度退化参数;φmax为支座可预计的最大损伤参数.根据文献[12],参数取值为k=10,φmax=1,α=0.75.

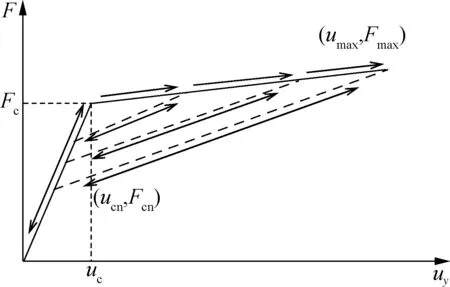
图1 拉伸模型示意图

1.3 弯曲、扭转性能

支座的弯曲与扭转特性对于其整体性能的影响较小,故本单元采用线性模型来简化考虑支座的弯曲与扭转性能[10],即

(14)

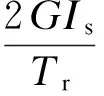
(15)

式中,Kb为弯曲刚度;Kr为扭转刚度;Is为支座截面的惯性矩;H为支座内部钢板层与橡胶层的总高度.

2 模拟分析

为了验证所提单元模型的有效性,下面针对文献[13-14]中的静、动力试验进行模拟分析,并研究了地震动作用下考虑压缩刚度与临界承载力随侧移的变化效应对于支座性能的影响.

2.1 静力水平双向位移控制试验模拟

为验证本单元模型对于支座水平双向耦合效应模拟的准确性,对文献[13]中铅芯橡胶支座双向位移控制试验进行模拟分析.支座规格如下:支座外直径为167.9 mm,内直径为29.97 mm;橡胶层的总厚度为19×3.175=60.325 mm,钢板层的总厚度为18×1.905=35.29 mm;支座总高度为151.77 mm;橡胶剪切模量G=0.64 MPa;支座的特征强度值Qd=6.786 kN.如图2(a)所示,该试验将质量为29 483.50 kg的质量块放置于4个支座上,并通过4个水平向支撑来固定该质量块,下部振动台台面按照相应的双向位移加载路径进行加载,以研究支座的水平双向耦合性能.下面针对方形加载路径(见图2(b))且位移幅值为60.3 mm(γ=100%) 这一试验工况进行模拟.

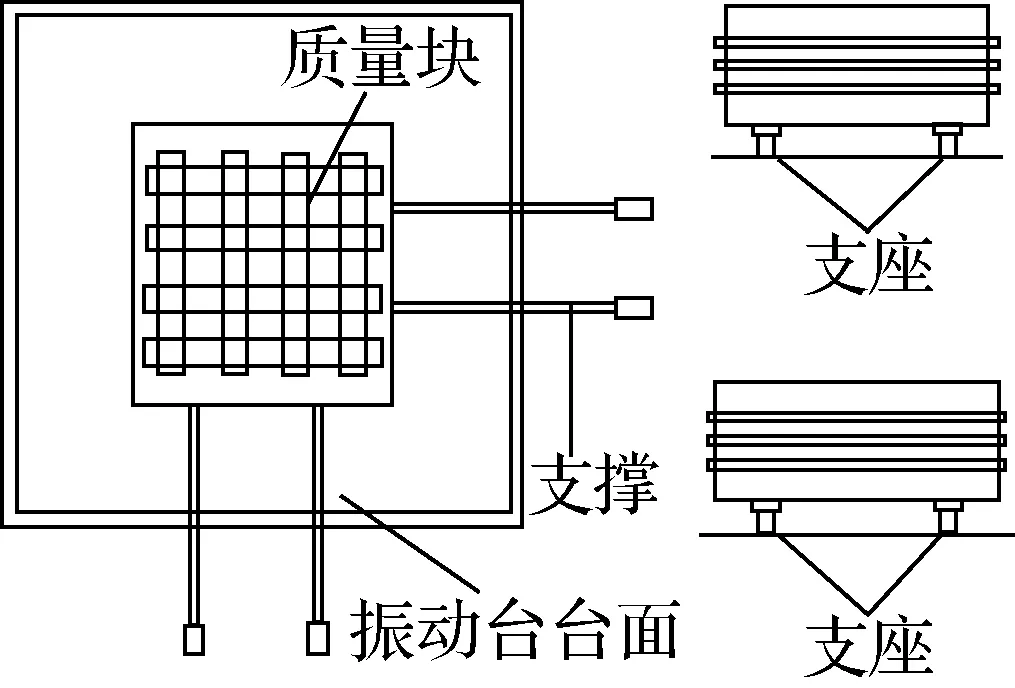
(a) 加载装置

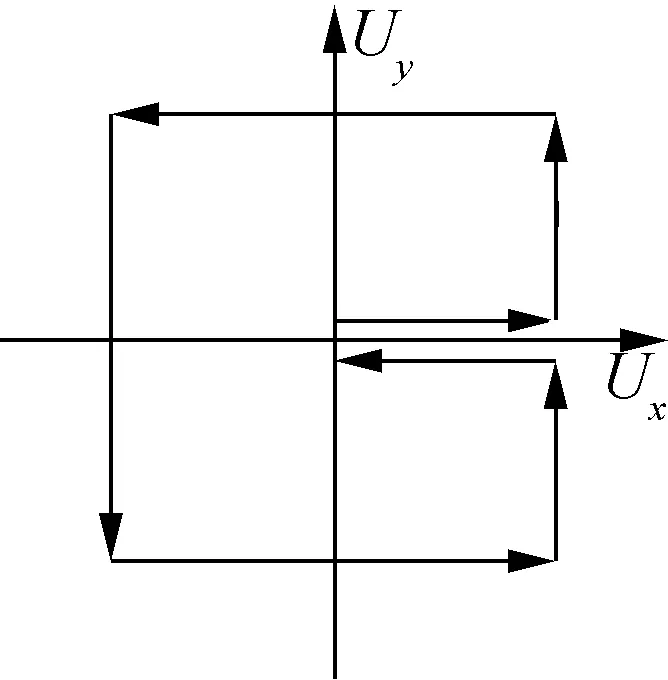
(b) 加载路径

试验与模拟结果对比如图3所示.由图可知,支座在水平面内表现出较强的双向耦合效应.当x向水平剪应变达到100%并保持不变时,随着y向位移的增加,x向恢复力随之减小,大约降至单向恢复力幅值的1/2(见图3(a)),该单元模型能够相对准确地模拟出恢复力双向耦合行为.Zx和Zy的时程曲线如图3(b)所示,初始屈服后支座的屈服面表现为圆形形状,且‖Z‖位于±1之间.x,y向滞回曲线的试验和模拟结果对比见图3(c)和(d),由图可知,在给定的水平剪应变范围内两者基本一致.

2.2 静力循环拉伸性能试验模拟

对文献[14]中铅芯橡胶支座的循环拉伸试验进行模拟分析.试验支座参数如下:外直径为152 mm,内直径为30 mm;单层橡胶的厚度为3 mm,共20层;单层钢板的厚度为3 mm;支座总高度为167 mm,橡胶的剪切模量G=0.82 MPa;特征强度值Qd=7 kN.静力循环拉伸加载制度如图4所示,分别以6, 30, 89 mm为位移幅值,每一位移幅值下加载3次,加载频率为0.01 Hz.

支座拉伸承载力-位移的试验与模拟结果对比如图5所示.由图可知,当拉伸位移幅值为6 mm时,支座处于线弹性状态,拉伸刚度基本不变,且加卸载路径保持一致.当位移幅值达到30和89 mm时,支座内部橡胶层出现孔洞损伤,导致支座拉伸刚度降低.在加卸载过程中,橡胶层的永久损伤表现出非线性耗能特性,故加卸载路径不再重合.本单元模型很好地模拟出循环拉伸荷载作用下支座永久损伤、强度退化等力学特征.

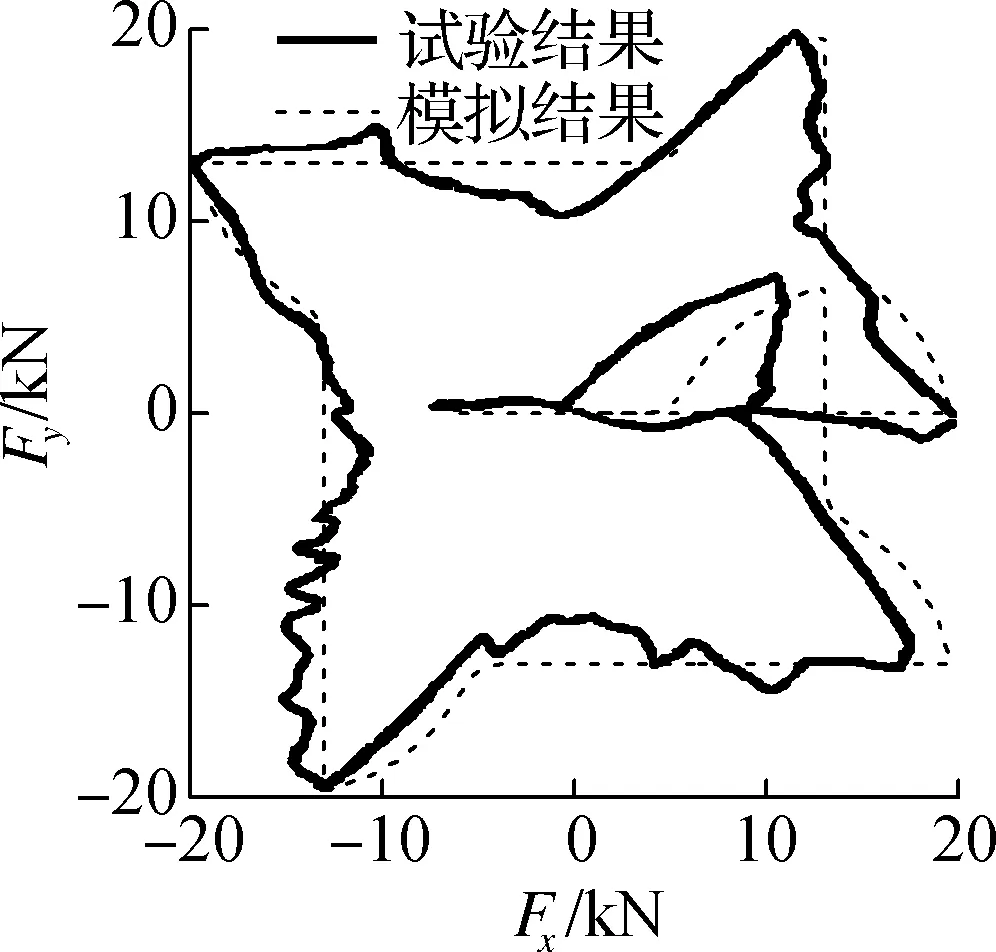
(a) 双向恢复力

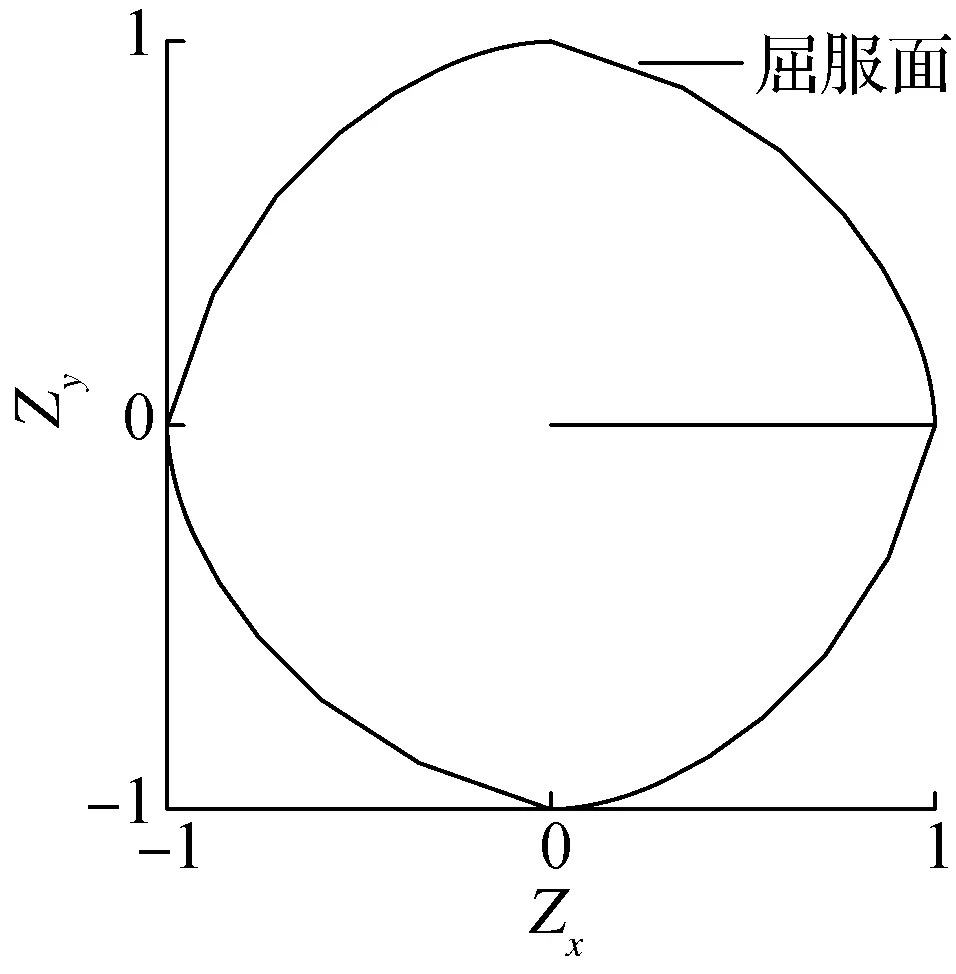
(b) 滞回位移Z

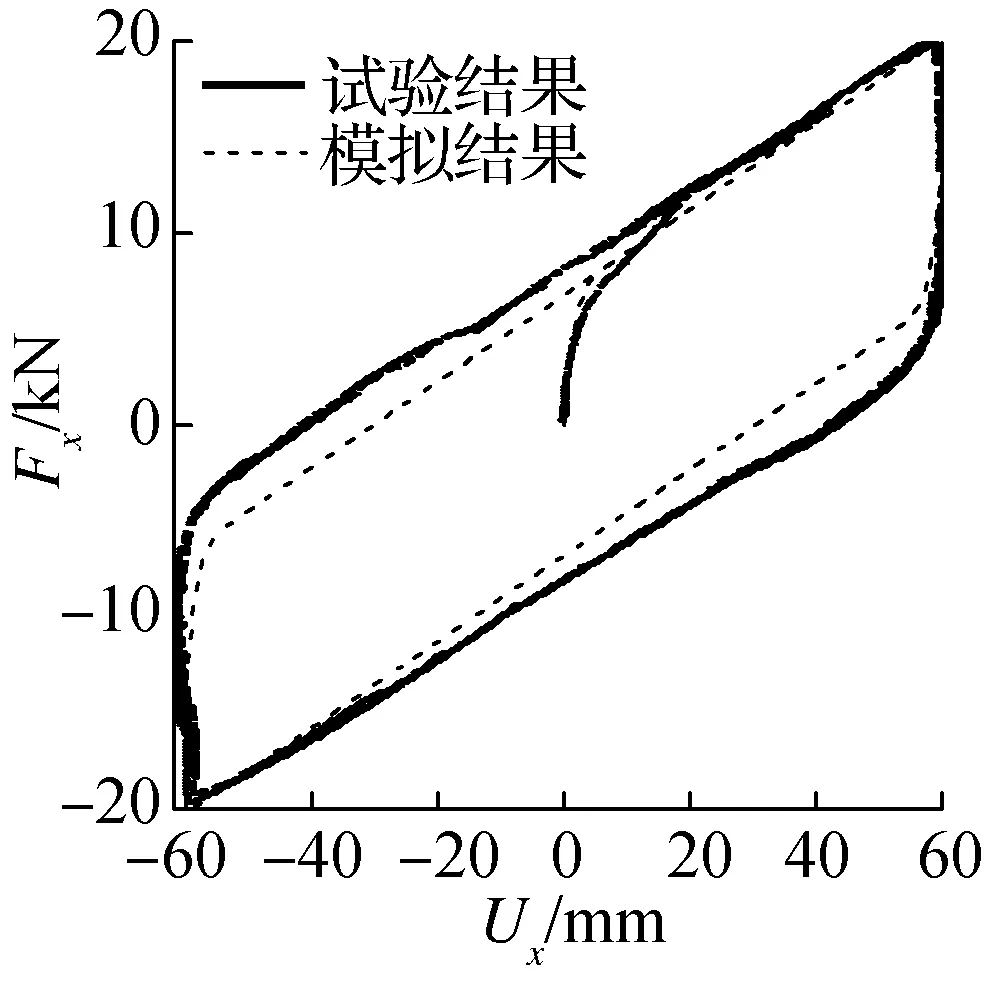
(c) x向滞回曲线

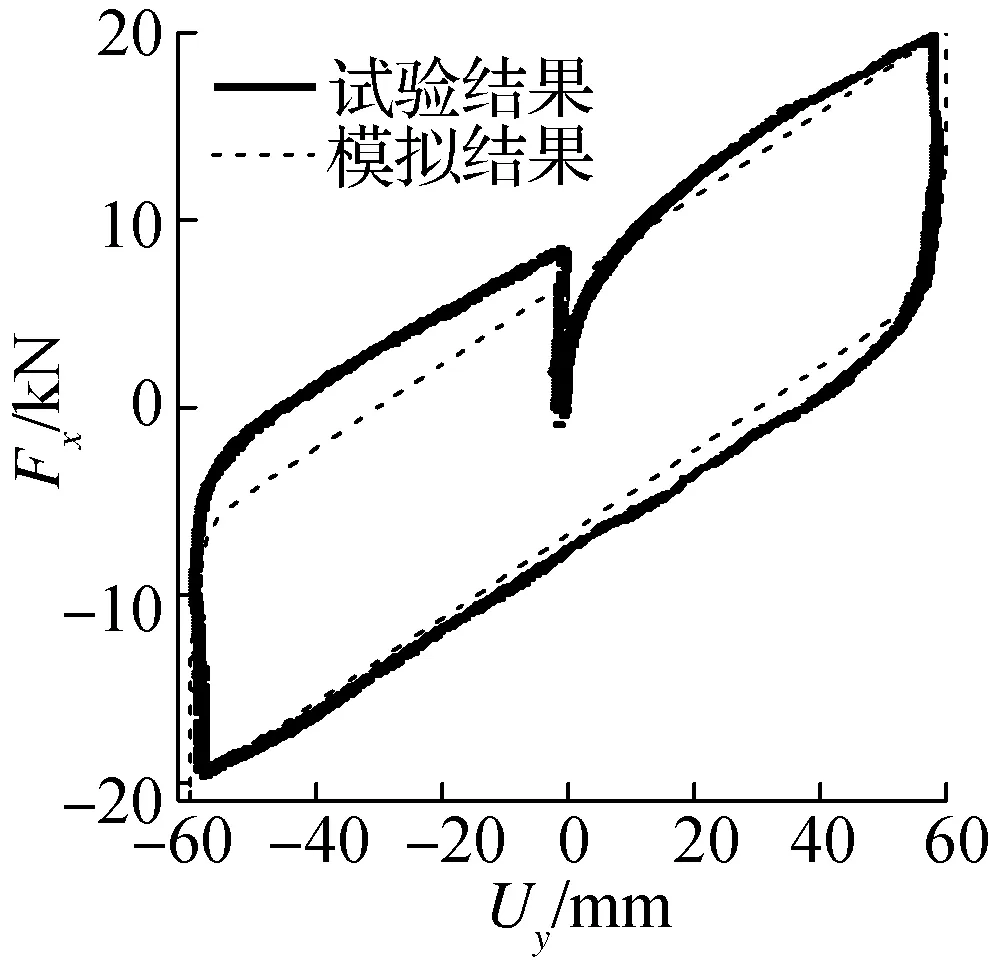
(d) y向滞回曲线

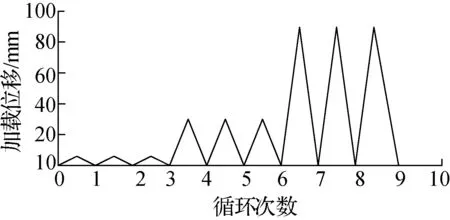
图4 静力循环拉伸加载制度

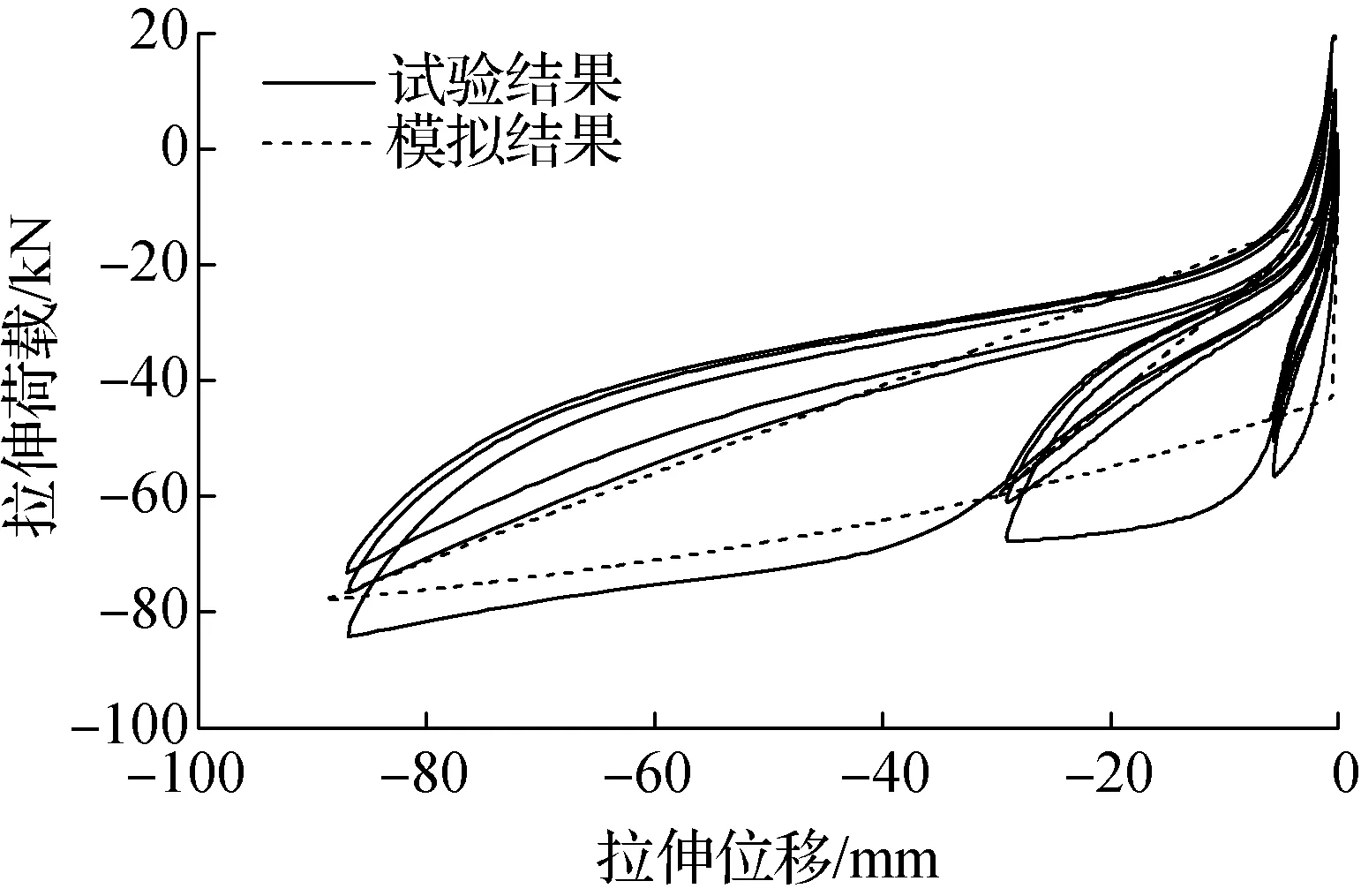
图5 隔震支座拉伸试验与模拟结果对比

2.3 隔震桥梁动力试验模拟

对文献[14]中钢桁架隔震桥梁模型振动台试验进行模拟分析.该试验分别进行了单向、双向和三向地震动输入,目的在于分析地震动竖向分量对于隔震桥梁地震响应的影响.本节仅针对三向地震动输入下的试验工况进行模拟分析.如图6所示,该桥梁模型长度为1.524×7=10.67 m,宽度为1.2 m,总高度约为2.3 m,桁架桥梁自重约89 kN,并设置附加质量块,使得模型上部结构总重量约为382 kN.共设置4个圆形铅芯橡胶支座,支座参数与静力循环拉伸试验所采用的支座规格相同.下面针对该隔震桥梁模型在Slymar (Northridge,1994)地震动记录输入下的响应表现进行模拟分析,时间相似比为0.5,PGA调幅比例为0.75,x、y和z方向上地震动PGA分别调至0.6g、0.81g和0.39g.

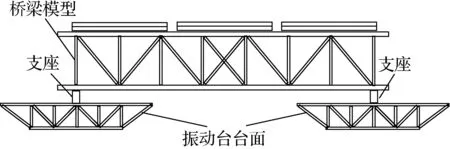
(a) 正视图

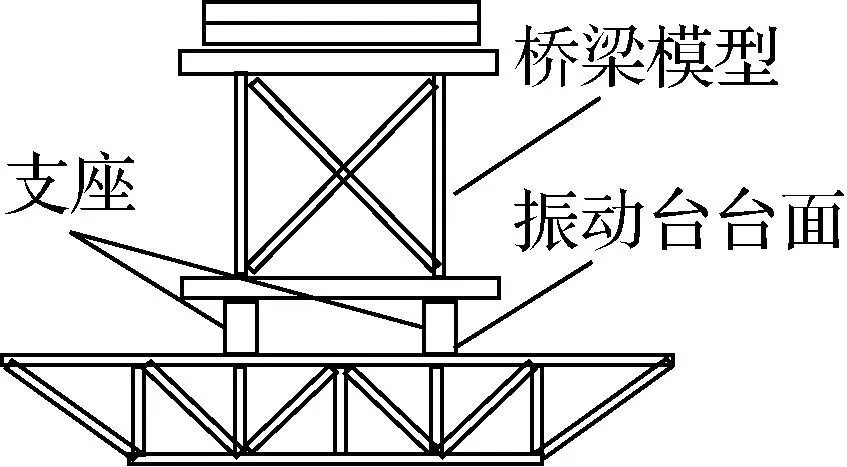
(b) 侧视图

图7给出了支座在x,y方向上力-位移关系的试验与模拟结果.对比分析发现,在不同的水平位移层次下,滞回曲线的模拟结果均能够与试验结果相吻合.

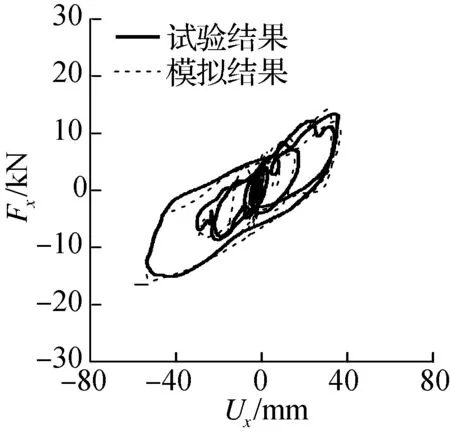
(a) x向

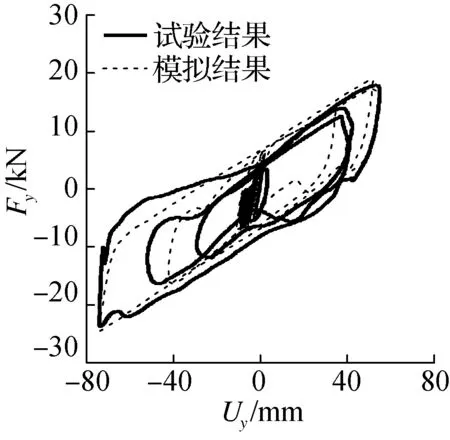
(b) y向

为体现出动力荷载作用下铅芯橡胶支座的水平双向耦合特性,提取Zx与Zy的时程曲线(见图8).由图可知,支座表现为圆形屈服面,且‖Z‖处于±1之间.如1.1节所述,非耦合模型表现为方形屈服面,从而在一定程度上高估了支座的地震需求.图9给出了支座双向恢复力的时程曲线.由图可知,本单元模型能够很好地反映出水平恢复力Fx与Fy之间的耦合现象.

图8 滞回位移的时程曲线

支座竖向刚度与竖向位移的时程曲线见图10.由图可知,支座初始竖向刚度值为157.055 kN/mm,在该地震动输入过程中,竖向刚度的最小值为77.716 kN/mm.竖向压缩位移的最大值与最小值分别为3.48和1.39 mm,支座的竖向位移变化较为显著.竖向刚度随侧移的变化效应对于混合隔震体系(如滑移支座与橡胶支座并联)显得尤为重要,因为当体系产生侧移时,2种隔震支座的竖向刚度比值发生变化,产生不同的竖向位移,引起各支座处竖向压力的重新分布,特别是滑移支座竖向压力的变化会影响到支座的水平摩擦力,进而影响上部结构的地震响应.因此,考虑竖向刚度的变化特性对于准确判别隔震结构的地震响应显得十分必要.

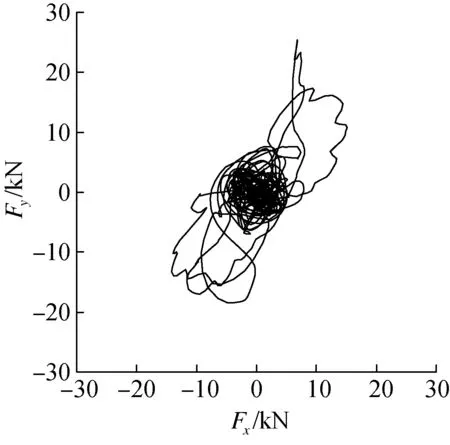
图9 水平双向恢复力时程曲线

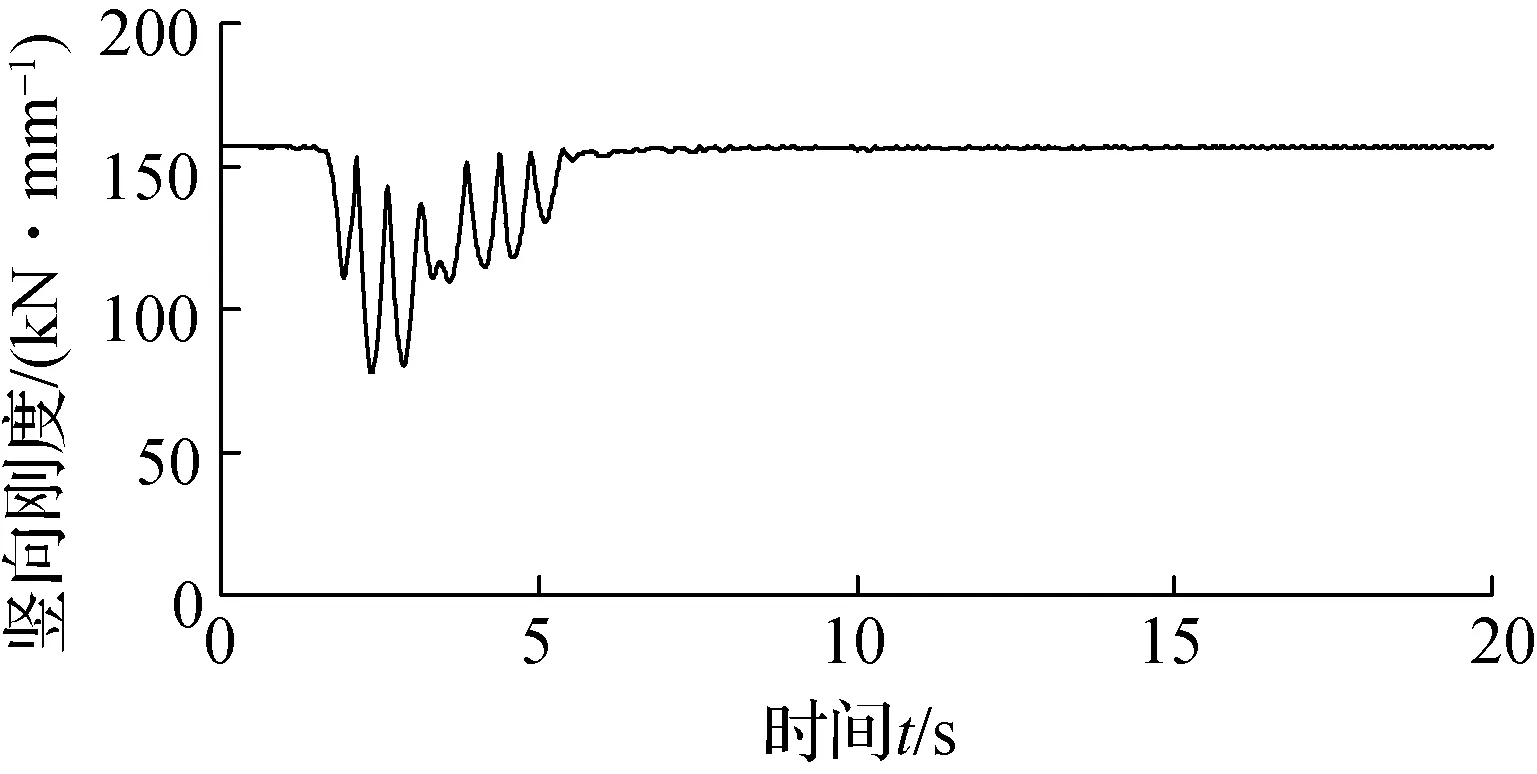
(a) 压缩刚度

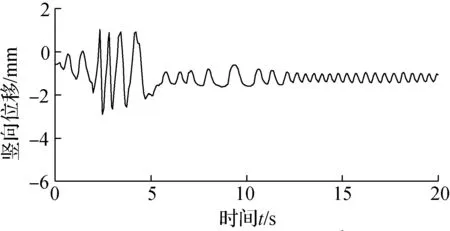
(b) 竖向位移

支座竖向压力与临界承载力的时程曲线见图11.鉴于竖向地震动分量及上部结构倾覆力矩的联合作用,支座竖向压力出现较大的波动,但始终小于支座的临界承载力,因而支座未发生失稳破坏.然而,支座在零侧移状态下的临界承载力为489.8 kN,随着侧移的不断变化,临界承载力最小值为 292.4 kN,支座临界荷载力发生较为显著的变化.因此,在某些工况下,若不考虑临界承载力的变化效应,将会高估支座的承载能力,从而不能有效识别支座的破坏模式.

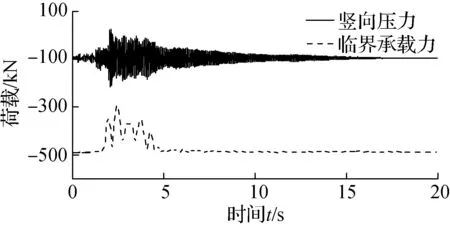
图11 临界承载力与竖向压力的时程曲线

3 结论

1) 本文基于OpenSees有限元程序开发了铅芯橡胶隔震支座单元模型,综合考虑了支座的水平双向耦合效应、竖向压力对水平刚度影响、竖向刚度和临界承载力随侧移的变化关系以及计入加载历程对于支座拉伸方向上累积损伤、强度退化等性能的影响,从而更加准确地把握支座在各个方向上的力学性能.

2) 与静、动力试验结果的对比分析说明,所提单元模型可以很好地模拟支座的水平双向耦合效应,从而准确预测支座的地震需求.

3) 不同于已有隔震单元模型,所提单元模型考虑了支座的非线性拉伸特性.通过与试验结果进行对比发现,本单元模型能够准确合理地把握支座的拉伸性能.

4) 随着水平位移的增加,铅芯橡胶支座的竖向刚度不断降低.本单元模型计入了竖向刚度的变化效应,有利于更加合理地预测混合隔震体系的地震响应.

5) 若不考虑支座临界承载力随着侧移变化的影响,可能会高估支座的承载力,无法有效判别支座的失效模式.

6) 所提单元模型合理地考虑了支座各方向上的力学性能,为进一步开展隔震结构整体精细化分析及其支座的失效模式判别研究提供了条件.

)

[1] Warn G P, Whittaker A S, Constantinou M C. Vertical stiffness of elastomeric and lead-rubber seismic isolation bearings [J].JournalofStructuralEngineering, 2007,133(9): 1227-1236. DOI:10.1061/(asce)0733-9445(2007)133:9(1227).

[2] Vemuru V S M, Nagarajaiah S, Masroor A, et al. Dynamic lateral stability of elastomeric seismic isolation bearings[J].JournalofStructuralEngineering, 2014,140(8): A4014014. DOI:10.1061/(asce)st.1943-541x.0000955.

[3] Koh C G, Kelly J M. A simple mechanical model for elastomeric bearings used in base isolation[J].InternationalJournalofMechanicalSciences, 1988,30(12): 933-943. DOI:10.1016/0020-7403(88)90075-6.

[4] Vemuru V S M, Nagarajaiah S, Mosqueda G. Coupled horizontal-vertical stability of bearings under dynamic loading[J].EarthquakeEngineering&StructuralDynamics, 2016,45(6):913-934.

[5] Maureira N, de la Llera J, Oyarzo C, et al. A nonlinear model for multilayered rubber isolators based on a co-rotational formulation[J].EngineeringStructures, 2017,131: 1-13. DOI:10.1016/j.engstruct.2016.09.055.

[6] Mckenna F, Fenves G, Scott M. Open system for earthquake engineering (OpenSees) [EB/OL]. [2016-10-19]. http://www.opensees.berkeley.edu.

[7] Park Y J, Wen Y K, Ang A H S. Random vibration of hysteretic systems under bi-directional ground motions[J].EarthquakeEngineering&StructuralDynamics, 1986,14(4): 543-557. DOI:10.1002/eqe.4290140405.

[8] Casciati F. Stochastic dynamics of hysteretic media [J].StructuralSafety, 1989,6(2/3/4): 259-269. DOI:10.1007/3-540-60214-3_60.

[9] Naeim F, Kelly J M.Designofisolatedstructures:Fromtheorytopractice[M]. New York, USA: John Wiley & Sons, 1999: 93-133.

[10] Kelly J M, Konstantinidis D A.Mechanicsofrubberbearingsforseismicandvibrationisolation[M]. New York, USA: John Wiley & Sons, 2011: 19-111.

[11] 中国国家标准化管理委员会. GB 20688.3—2006 橡胶支座 第3部分:建筑隔震橡胶支座[S]. 北京:中国标准出版社,2006.

[12] Kumar M. Seismic isolation of nuclear power plants using elastomeric bearings [D]. New York, USA: Department of Civil, Structural and Environmental Engineering of State University of New York at Buffalo, 2015.

[13] Huang W H. Bi-directional testing modeling, and system response of seismically isolated bridges [D]. Berkeley, CA, USA: Department of Civil and Environmental Engineering of University of California, 2002.

[14] Warn G P. The coupled horizontal-vertical response of elastomeric and lead-rubber seismic isolation bearings [D]. New York, USA: Department of Civil, Structural and Environmental Engineering of State University of New York at Buffalo, 2006.

Developmentandverificationofelementmodelforlead-rubberbearings

Zhou Tong1Li Aiqun1,2,3

(1School of Civil Engineering, Southeast University, Nanjing 210096, China) (2Beijing Advanced Innovation Center for Future Urban Design, Beijing 100044, China (3School of Civil and Transportation Engineering, Beijing University of Civil Engineering and Architecture, Beijing 100044, China)

To improve the accuracy and the efficiency of mechanical property calculations and analyses of lead-rubber bearings, the corresponding element model is proposed based on the OpenSees program. This model accounts for the coupled bidirectional response and the isotropic behavior of circular bearings. Furthermore, the variation of the compression stiffness and the critical load with the change of lateral displacement and the effects of the loading history on the cumulative damage and cavitation strength reduction in the tensile direction of bearings are considered. To validate the effectiveness of this element model, simulation analyses are conducted for the bi-directional displacement-controlled tests, the cyclic tensile load tests and the steel-truss isolated bridge dynamic tests, respectively. The results show that this numerical model can reasonably simulate the mechanical behaviors of bearings. The response performance of the bearings under earthquake ground motions can be described accurately by considering the variation of the bearings’ mechanical characteristics. The proposed model provides a foundation for further investigation of the response analyses on seismic isolated structures.

lead-rubber bearings; horizontal bidirectional coupling; vertical compression stiffness; verification

10.3969/j.issn.1001-0505.2017.06.012

TU352.1

A

1001-0505(2017)06-1154-07

2017-03-07.

周通(1993—),男,硕士生;李爱群(联系人),男,博士,教授,博士生导师,aiqunli@seu.edu.cn.

国家自然科学基金重点资助项目(51438002)、国家自然科学基金资助项目(51278104).

周通，李爱群.铅芯橡胶支座单元模型的开发及验证[J].东南大学学报(自然科学版),2017,47(6):1154-1160.

10.3969/j.issn.1001-0505.2017.06.012.