比例边界有限元法求解裂纹面接触问题1)
2017-12-18杜成斌江守燕
章 鹏 杜成斌 江守燕
(河海大学工程力学系,南京211100)
比例边界有限元法求解裂纹面接触问题1)
章 鹏 杜成斌2)江守燕
(河海大学工程力学系,南京211100)
比例边界有限元侧面上有任意荷载时,将侧面载荷分解成关于径向方向局部坐标的多项式函数的和,推导给出了考虑侧面载荷存在的新型形函数,并基于该形函数推导了刚度矩阵和等效节点载荷列阵.首次对比例边界有限元法求解裂纹面接触问题进行了研究,运用Lagrange乘子引入接触界面约束条件,推导给出了比例边界有限元求解裂纹面接触问题的控制方程.将裂纹面单元分为非裂尖单元和含有侧面的裂尖单元.在非裂尖单元中的裂纹面,裂纹面作为多边形单元的边界,边界上的接触力可等效到节点上,通过在节点上构造Lagrange乘子,采用点对点接触约束进行处理.对于含有侧面的裂尖单元,在整个侧面上构造Lagrange乘子的插值场,采用边对边接触约束进行处理.对三个不同的接触约束状态下的算例进行了数值计算,通过与解析解及有限元软件ABAQUS计算结果的对比,验证了本文提出的比例边界有限元点对点和边对边接触求解裂纹面接触问题的精确性与有效性.
比例边界有限元,形函数,裂纹,点对点接触,边对边接触
引言
在工程实际中,由于各种原因,工程结构或多或少都存在着裂缝(纹)[1].在外力作用下,既存在受拉状态的张开型裂纹,也有压剪状态的闭合型裂纹.用数值方法分析闭合型裂纹时,需要在裂纹面上施加合适的接触条件,以反映裂纹面间的接触状态,否则裂纹面会发生与实际不符的相互嵌入现象[2-3].目前施加接触条件的方法主要有Lagrange乘子法[4-5],增广的Lagrange乘子法[6],罚函数法[7-8],线性互补法[9]等.
比例边界有限元法(scaled boundary fi nite element method,SBFEM)是由Wolf和Song在20世纪90年代末率先提出和发展起来的一种半解析的数值计算方法[10-11].该方法在计算过程中仅需离散结构的边界,降低了数值模拟维度,而且可以半解析地表征裂纹尖端的奇异性[12-14].基于上述优点,SBFEM在工程问题方面的应用正逐渐成为学术研究的前沿和热点[15-18].比例边界有限单元可以为含有任意边数的多边形,该特点也使在求解裂纹扩展时重划分网格具有简单性和高效性.Ooi等[19]推导给出了不考虑侧面载荷存在的多边形SBFEM位移形函数,并利用该形函数,推导了采用SBFEM求解弹塑性问题的有关公式,拓宽了SBFEM的应用范围,使得SBFEM可以求解一些非线性问题.
接触问题属于典型的非线性问题,在有限元法[20-21]、扩展有限元法[22-23]、边界元法[24]中已经得到了较长时间的发展.但是在各种方法中或多或少存在一些问题,有限元求解裂纹问题时,因为裂纹的不连续性,需要将裂纹定义在单元边界上,且在裂尖区域需要划分非常细的网格来反映应力奇异性,这将很大程度上降低求解裂纹接触问题的效率.扩展有限元中裂纹位于单元内部,采用点对点接触方案不能正确的表示裂纹面接触,只能采用砂浆法(mortar method)或边对边(segment-to-segment)接触方法来求解裂纹面接触应力,对每一个裂纹面单元都需数值积分求解,且对于裂尖单元的接触应力只可假设为恒定值[22],这将很大程度上降低接触应力的求解精度.边界元法求解接触较有优势,但是其本身方法需要求得严格满足控制方程的基本解,不适于对非均质、非各向同性介质的求解,还需进一步发展研究.比例边界有限元作为一种新型的高精度的数值方法,尚未发现有文献采用该方法求解裂纹面接触问题.采用SBFEM求解裂纹面接触问题时会遇到缝面存在载荷的情况,如缝面接触应力等.所以首先必须给出侧面存在载荷的比例边界有限元的有关列式.本文将任意侧边载荷表示为关于径向坐标ξ的多项式函数[25-26],推导了含有侧面载荷影响的SBFEM的形函数,并给出了相应的刚度矩阵以及等效载荷列式.将裂纹面单元分为非裂尖单元和含有侧面的裂尖单元.对于不含有裂尖的单元,裂纹面位于单元边界上,在节点上构造Lagrange乘子,采用点对点约束模拟裂纹面的接触.对于含有裂尖的单元,其裂纹面位于裂尖单元的侧面(side faces)上,由于侧面为非边界面,按常规思路施加点对约束不能正确的表示裂纹面接触,因此本文提出了在裂尖单元的裂纹面上采用边对边约束方法处理接触问题,即在整个侧面上构造Lagrange乘子的插值场,Lagrange乘子呈线性变化,通过Lagrange乘子推导出了SBFEM接触控制方程.通过若干不同的算例,验证了采用多边形SBFEM点对点--边对边接触可精确的模拟含有裂尖单元的接触问题.
1 含有侧面载荷的比例边界多边形有限元支配方程
1.1 考虑侧面载荷的比例边界多边形有限元的形函数
图1为一个含有裂纹的任意多边形,采用4个任意多边形SBFEM单元[27]进行离散,其中子域1包含裂纹信息(裂纹单元).根据比例边界有限元的单元形态要求,在每一个单元子域内,均需要选取一个比例中心,通过此中心该子域的全部边界都可见[28].处理复杂结构问题时,可通过合理布置比例中心位置将模型离散成多个多边形子域来满足这一基本要求.
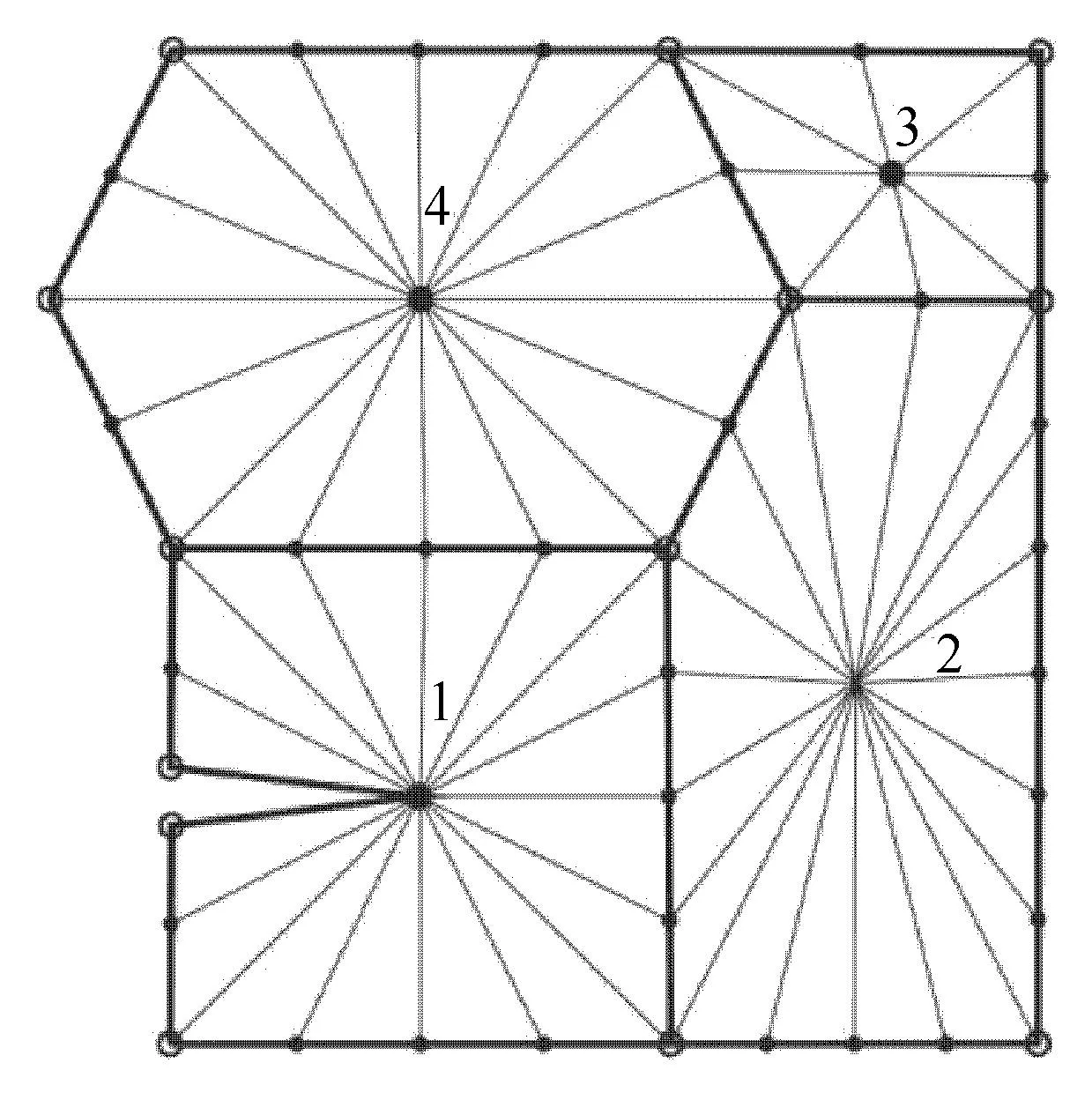
图1 比例边界有限元多边形离散模型Fig.1 Scaled boundary fi nite element method polygon discrete model
图2为具有裂纹面任意载荷的比例边界有限元单元模型,O(裂尖)为比例中心,断裂问题比例中心通常选在裂尖处,定义ξ(0 6ξ6 1)为径向坐标,s(0 6s6 1)为环向坐标,模型边界(ξ=1)离散成一维线单元,而裂纹侧面(side faces)不需要离散.ξ−s形成比例边界有限元局部坐标系.其中环向坐标s正向沿着单元边界逆时针变化[11],径向坐标ξ正向沿着比例中心向外变化,其中ξ=0代表比例中心O,ξ=1代表边界上的点.
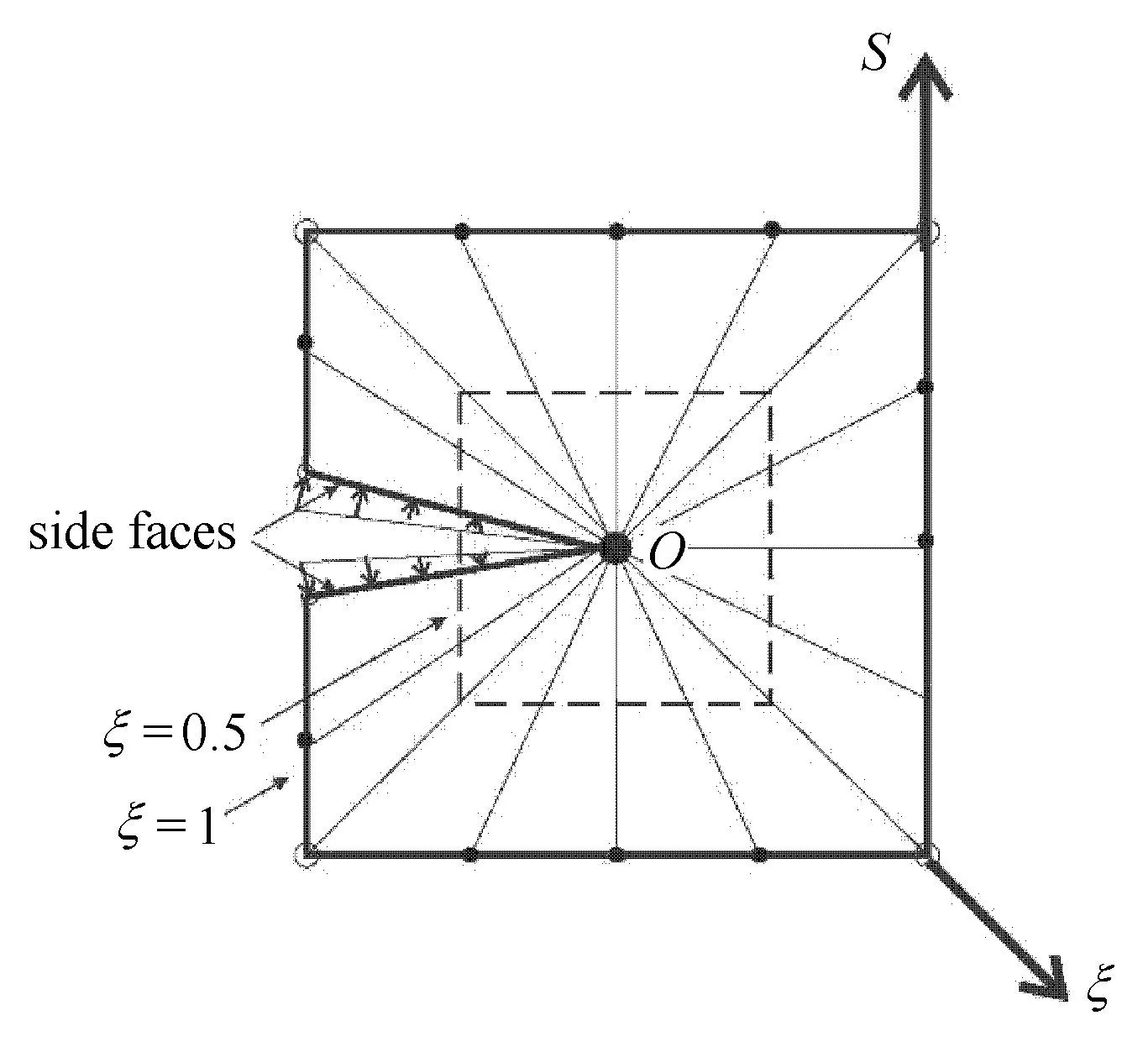
图2 比例边界有限元裂纹单元模型(•为比例中心,◦为顶点,·为节点)Fig.2 Scaled boundary fi nite element method crack element model(• scaling centres,◦ vertices,·nodes)
对于裂纹单元内任意一点,相对于比例中心的局部坐标(x,y)T可用ξ和s表示为
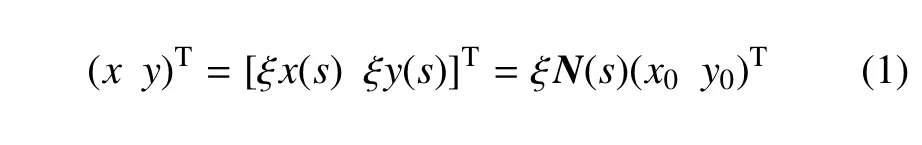
其中,(x0y0)为边界上的节点坐标.N(s)表示为沿s方向的形函数
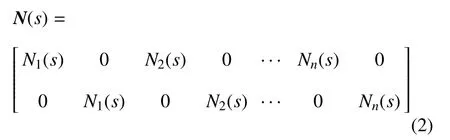
其中n为边界节点个数.
考虑侧面载荷的比例边界有限元的控制方程可通过加权平均法[7]或者虚功原理[8]得到
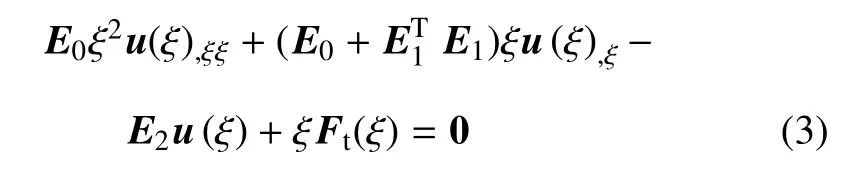
该方程为径向上的平衡方程.其中E0,E1,E2为单元的系数矩阵,Ft(ξ)为侧面载荷,u(ξ)为节点位移函数.
式(3)为含有2n个未知数u(ξ)的二阶微分方程,可化为一阶微分方程
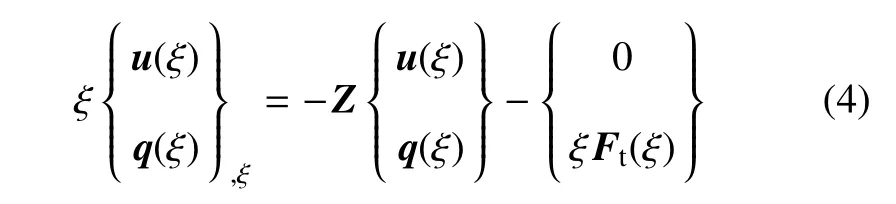
其中q(ξ)为内部节点力,Z为2n×2n阶Hamiltonian矩阵,满足
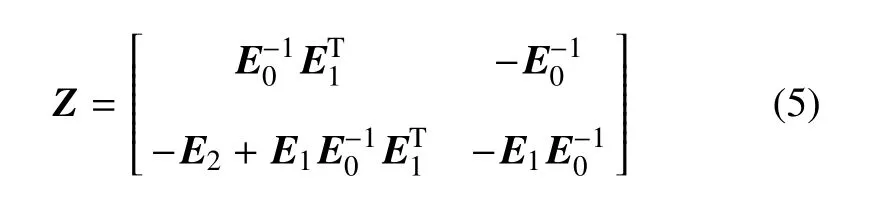
采用Schur分解[29]
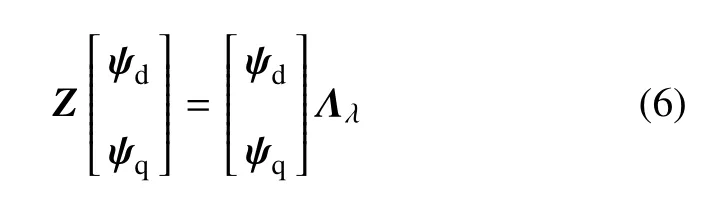
得到单元的模态位移ψd,模态载荷ψq及对应的特征值矩阵Λλ.
裂纹侧面上的任意载荷可以分解为关于ξ的M阶多项式函数[25]
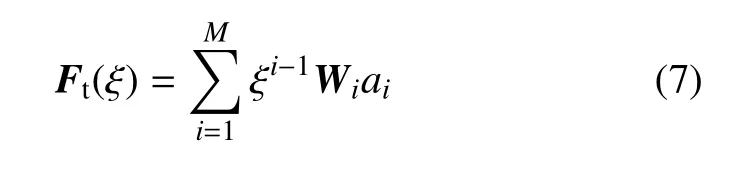
式中Wi为单元侧边力分布矩阵,ai为第i阶多项式系数.
侧面载荷的第i阶位移模态[11]为
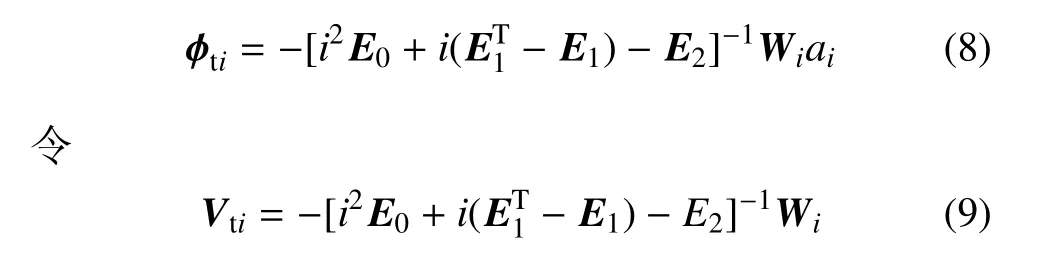
则径向位移解为
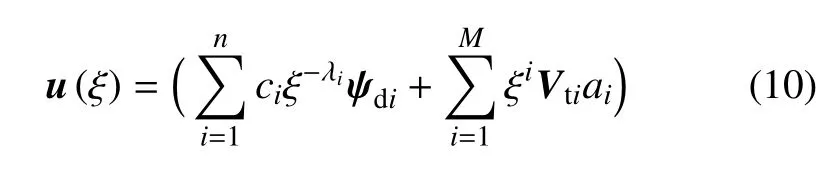
式(10)中第1项为式(3)的齐次通解.
式(10)的矩阵形式为

其中Λλ为特征值矩阵,Λt=dig(1,2,3···,M),a为ai组成的系数向量,c为积分常数,由边界条件确定.
边界上的节点位移为
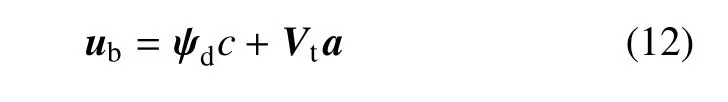
其中积分常数c用边界位移表达为
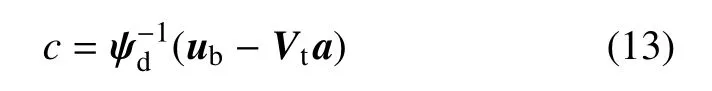
将式(13)代入式(11)可得
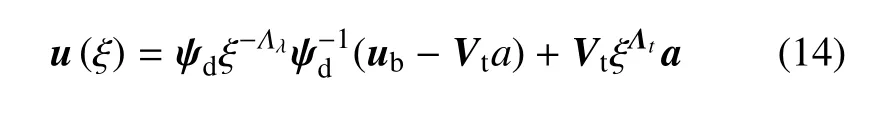
式(14)的矩阵形式可写为

将式(15b)和式(15c)代入式(15a)可得
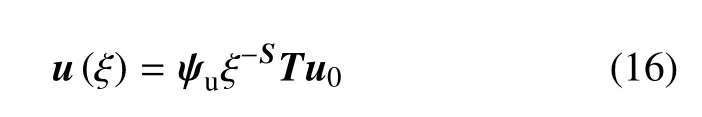
比例边界有限元在环向s上采用与有限单元法中形函数类似方法,通过N(s)进行插值,即
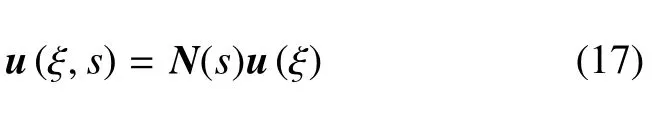
将式(16)代入式(17)可得
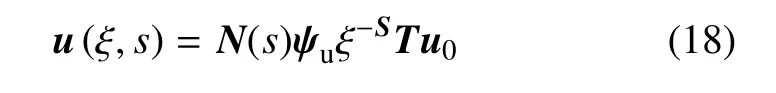
令
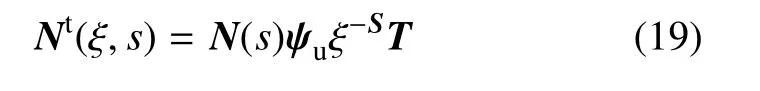
可得
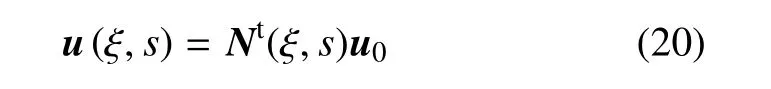
由式(20)可知,Nt(ξ,s)为采用比例边界有限元法考虑侧面任意载荷时的形函数.将式(19)各变量代入式(15b)和式(15c)得到
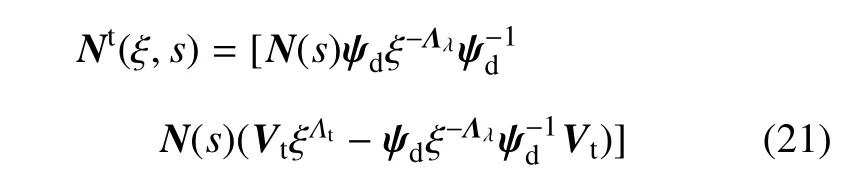
对于不考虑侧面载荷的比例边界元形函数为[16]
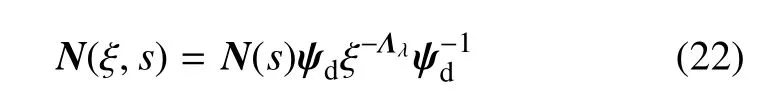
由式 (21)和式 (22)对比可看出Nt(ξ,s)左半部分N(s)ψdξ−Λλψ−1d为不考虑侧面载荷的形函数,右半部分为多项式函数
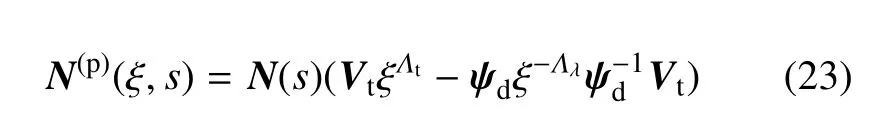
该多项式函数可看作是由侧面载荷对位移模式的影响,式(16)u0中的a作为特解位移的值,可看作为额外自由度.式(22)和式(23)两部分组成了考虑侧边力任意载荷时的形函数.从中可看出,无侧面载荷的形函数为考虑侧面载荷的形函数的一个特例,即a=0.
SBFEM的应变矩阵[11]为
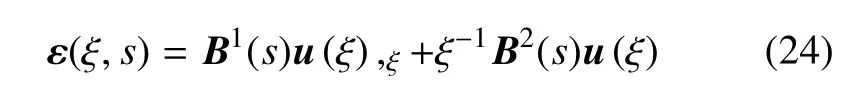
其中B1(s)和B2(s)是应变位移矩阵.
将式(16)代入式(24)得
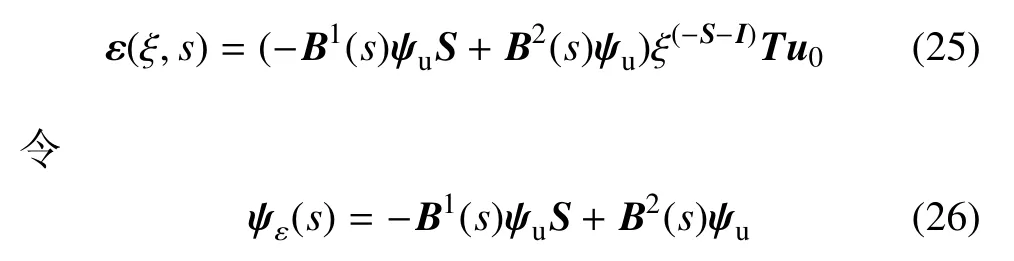
引入应变位移矩阵
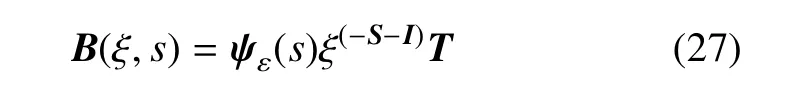
应变矩阵可写为
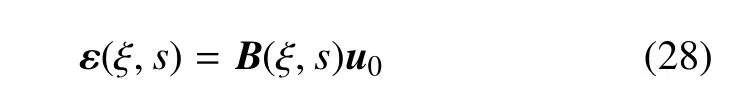
应力矩阵为
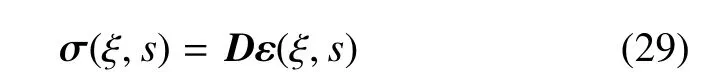
其中D是材料的弹性矩阵.
1.2 比例边界多边形有限元支配方程
考虑面载荷和侧边载荷时,采用虚功原理的表达式为
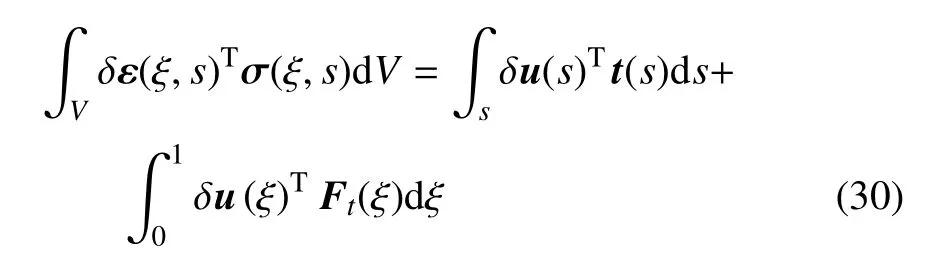
式中t(s)为边界上的面力[11],其他符号同前.
将式(20)、式(28)、式(29)代入式(30)得

式(31)等价为
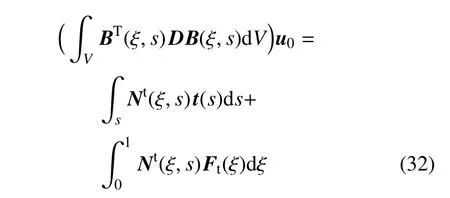
式(31)中左边括号部分可视为刚度矩阵,即
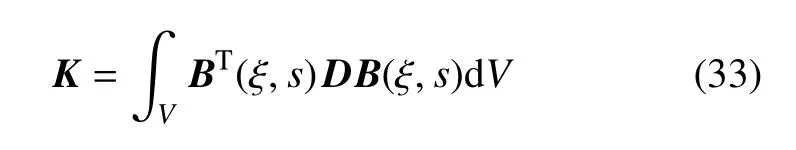
将式(27)代入式(33)可得

将dV进行积分得到
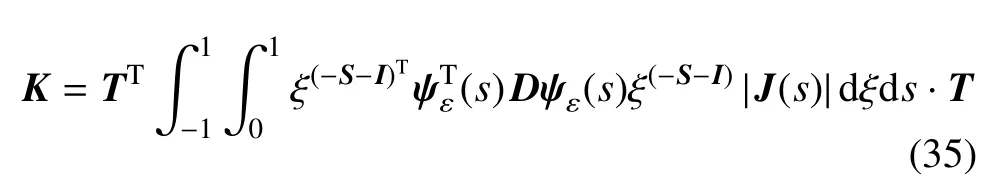
定义矩阵Y
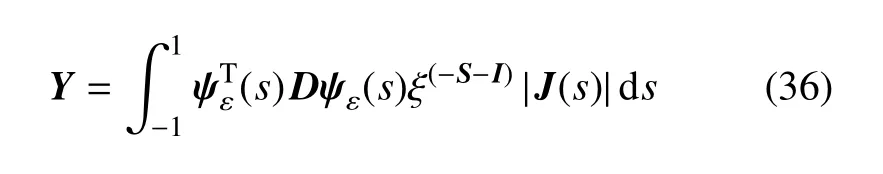
式(36)可以采用高斯积分或者Guass-Lobatto-Legendre积分[30]方法进行积分求解.
考虑式(36),式(35)可改写为
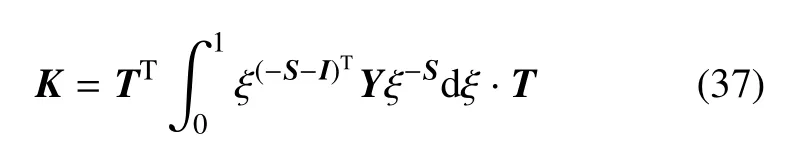
定义矩阵X
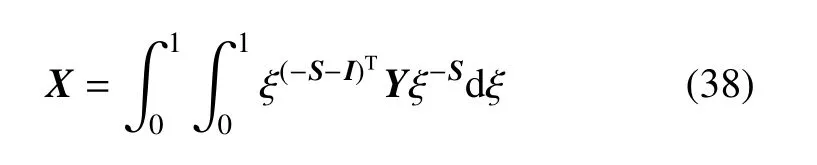
采用分部积分,式(38)可化简为Lyapunov方程[31]
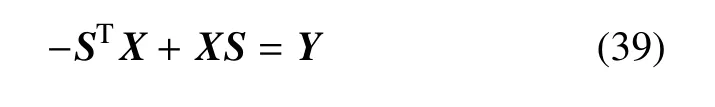
式(39)可通过Matlab自带函数求解Lyapunov方程,得出矩阵X.
将式(38)代入式(37)得出刚度矩阵K

式(32)中等式右侧为等效节点载荷Fp
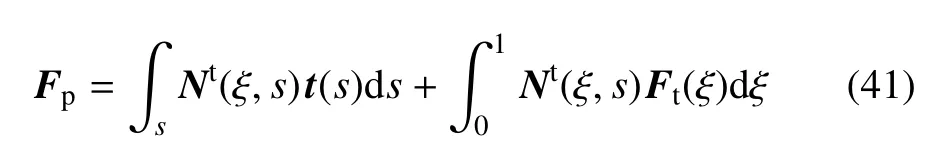
将式(33)、式(41)代入式(31)中可得到考虑侧面载荷的比例边界有限元支配方程

2 接触问题的有关公式
两物体接触受压时,在物体表面需引入物体表面的接触条件,以避免物体发生相互侵入[32].如图3所示,考虑二维问题,可能发生接触的两个表面记为SA和SB,为了系统地分析两物体表面的接触条件的施加方法,建立局部坐标系,设xA为SA上任一指定点P的坐标,则该点至SB面上最接近点Q的法向相对距离gN为
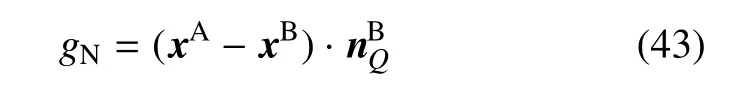
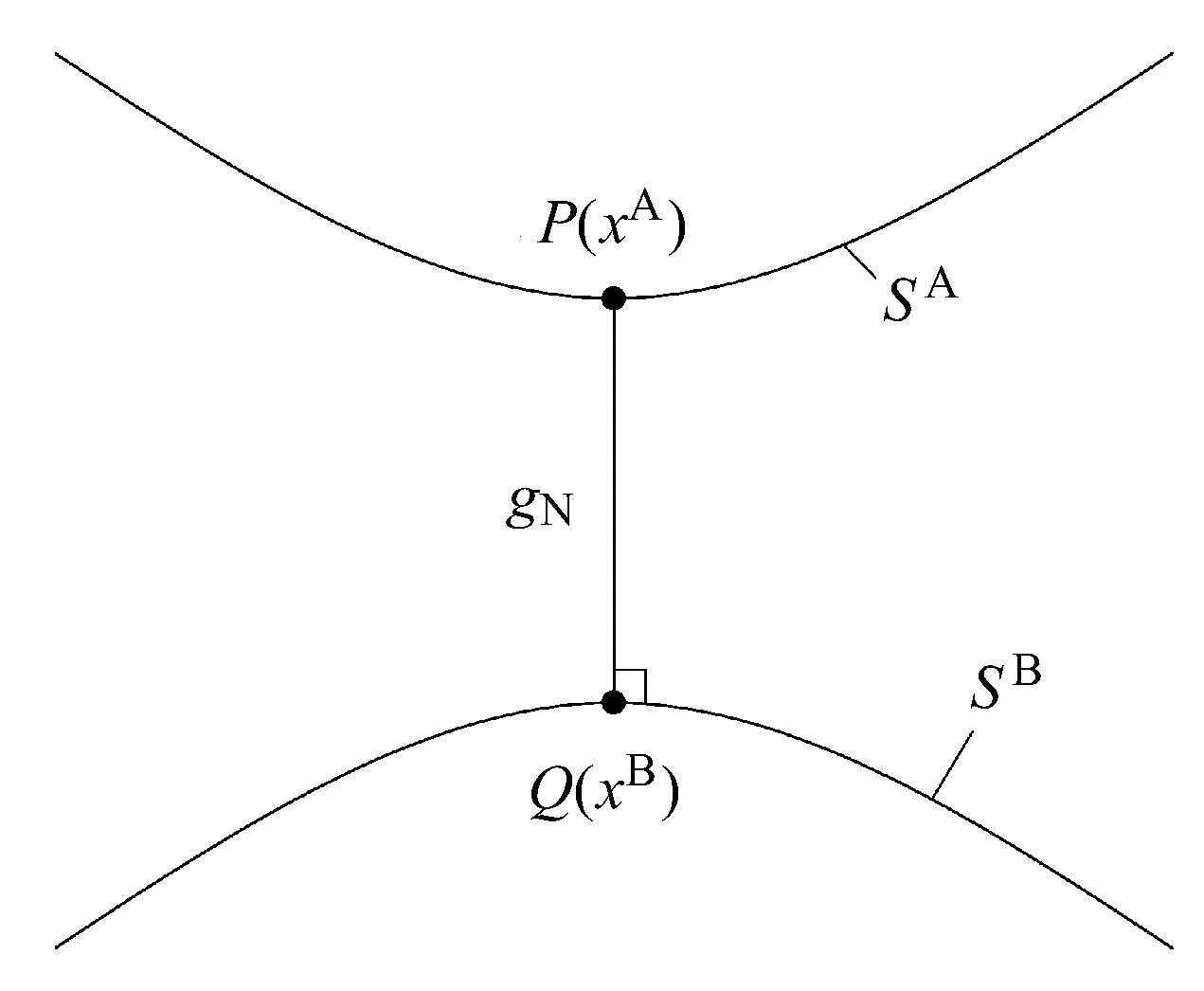
图3 接触点对与点对间的距离Fig.3 The contact points and distance between the points
同理定义切向相对距离gT
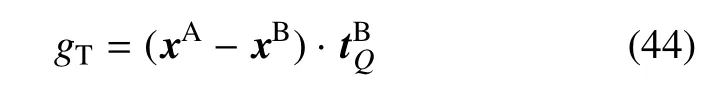
对于弹性接触问题,满足Coulomb定律的接触力和物体相对距离的关系可用下列等式和不等式[33]表示
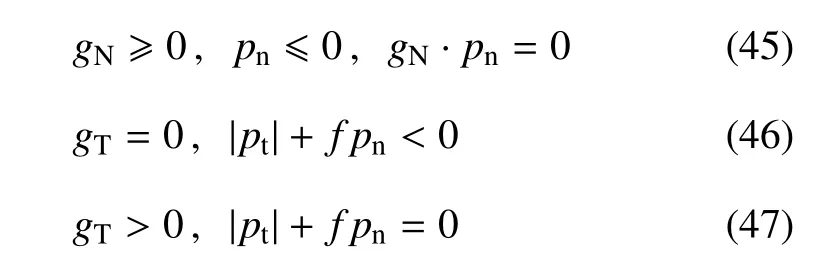
接触问题可描述为求区域内位移场,使得系统的势能达到最小.Lagrange乘子法[4]是求解接触约束最小化问题的常用方法之一,通过引入Lagrange乘子将接触问题转化为无约束问题求解.接触状态有3种:张开、粘结、滑移.法向Lagrange乘子场λN表示当接触发生时迫使gN等于0(裂纹面接触但无嵌入)的压力.在裂纹面为粘结接触时,切向Lagrange乘子场λT表示在粘结区迫使满足粘结条件的切向力,在裂纹面发生滑移接触时,切向Lagrange乘子场λT表示为滑移的摩擦力.
应用Lagrange乘子法在物体表面考虑摩擦接触条件时可导出3个方程:
(1)接触不嵌入条件
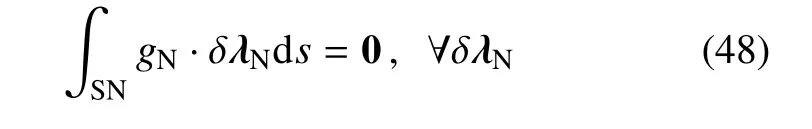
(2)在切向满足粘结条件时,即
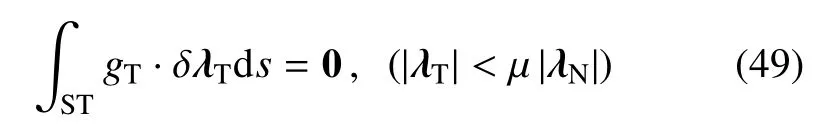
在切向满足有摩擦的滑动接触状态时:切向运动不再受约束,但是切向力满足
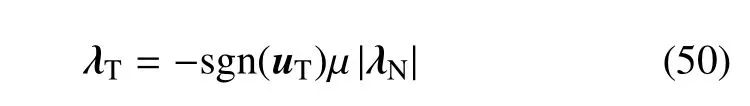
(3)虚功原理(外力虚功包括接触应力),即
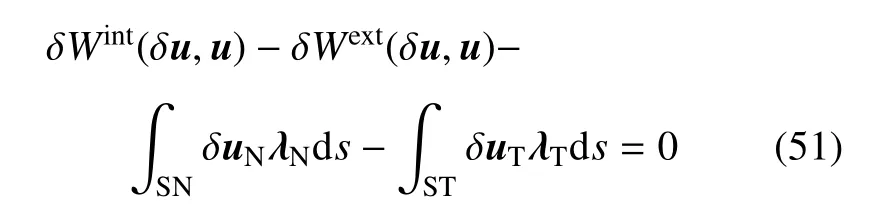
3 基于比例边界有限元求解摩擦接触问题
3.1 接触约束公式
如图4所示为比例边界有限元网格,假设满足粘结接触,则法向在粘结约束条件下,裂纹面上的P点和Q点法向接触间距为0.根据式(48)可得
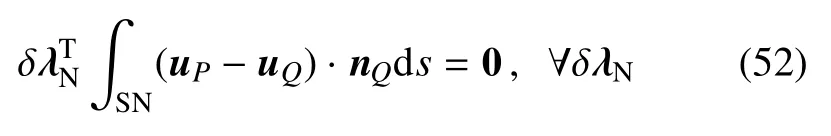
其中外法向向量nQ={−sinαcosα}T.
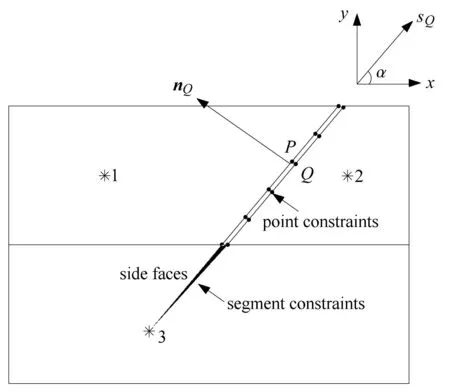
图4 点对点与边对边约束示意图Fig.4 Point-to-segment constraints diagram
切向方向上,在粘结接触条件下,根据式(49)可得
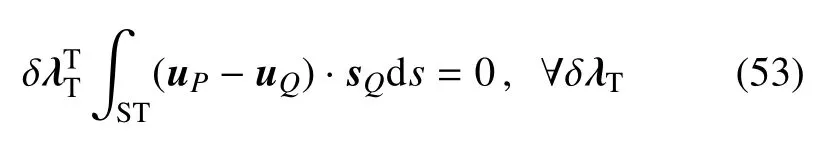
正切向向量sQ={cosαsinα}T.
3.1.1 不含裂尖的裂纹面单元
在不含裂尖的裂纹面单元中,如图4的第1,2个单元,裂纹面接触分别在两个单元的边界上(ξ=1),在该边界上其形函数N(s,ξ=1)=N(s)只是关于s的函数,可以采用虚功原理将边界上的接触应力等效到该裂纹面边界节点上,边界节点上的接触载荷为等效节点载荷.所以只需点约束即可精确模拟接触,在节点上构造Lagrange乘子(λN,λT),则在第k个点对P点和Q点间,式(52)可写为
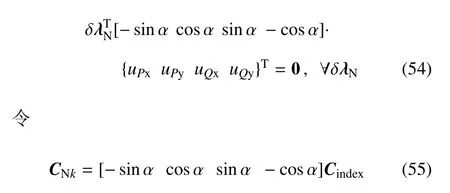
其中,CNk为矩阵CN第k行,Cindex为点对P和Q两节点在整体节点中的坐标变换.
由式(54)可得裂纹面点对点接触法向方向约束方程

同样在切向方向,令
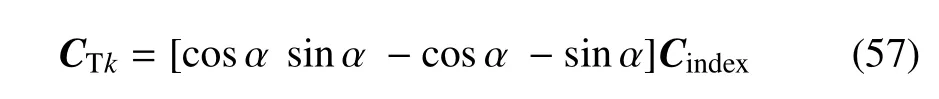
可得裂纹面点对接触切向方向约束方程

3.1.2 包含裂尖的裂纹面单元
将含有裂尖单元的比例中心放在裂尖处,如图4的单元3所示.在该单元的裂纹面侧面(side faces)上,ξ从0变化到1,该单元所受的裂纹面接触应力为侧面应力.该侧面的形函数Nt(ξ,s)为关于(ξ,s)的函数,因为此时裂纹面为非边界面(ξ(0 6ξ6 1)),按常规思路施加点对约束不能正确地表示裂纹面接触.为此本文提出了在裂尖单元中采用边对边接触方法,即在整个侧面上构造Lagrange乘子的插值场,Lagrange乘子呈线性变化,其插值可表示为
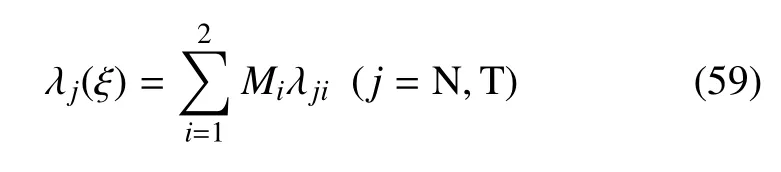
其中,λj1为侧边中心(裂尖中心)的接触应力,λj2为侧边端点的接触应力.
Mi为Lagrange乘子插值函数
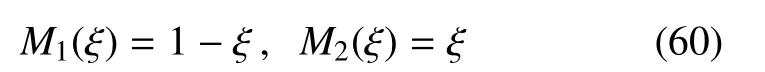
则式(52)可写为
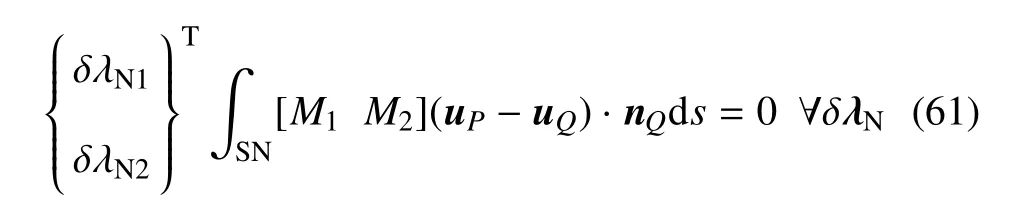
由式(19)形函数可知
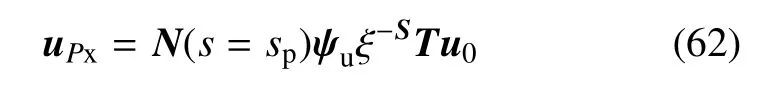
同理可求出uPy,uQx,uQy代入式(61)并进行运算积分可得
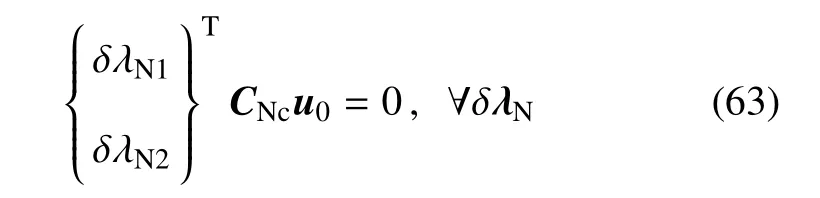
其中CNc为考虑式(61)和式(62)运算积分所得.
最终得到裂尖单元边对边接触法向约束方程

同理可得到裂纹侧面边对边接触切向方向约束方程

考虑插值得到的Lagrange乘子,式(51)的虚功方程用矩阵形式可表示为
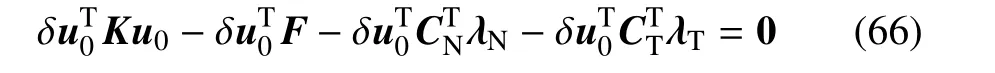
其中,K和F为SBFEM的刚度矩阵和载荷列阵,u0为SBFEM位移列阵;λN和λT为法向和切向Lagrange乘子.
根据虚功方程(66)和前文所得的约束方程,假设裂纹面满足粘结接触条件,则系统的控制方程为
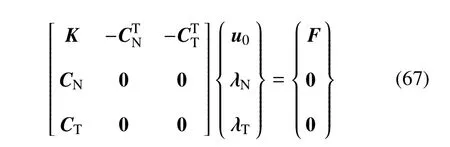
式(67)第1行为虚功方程推导出的平衡方程,第2行为法向接触条件,第3行为切向粘结接触条件.在满足有摩擦的滑移条件的状态下,其切向运动不受约束,即式(67)第3行将不再成立.而切向摩擦力满足式(50).
故满足滑动接触状态的控制方程为
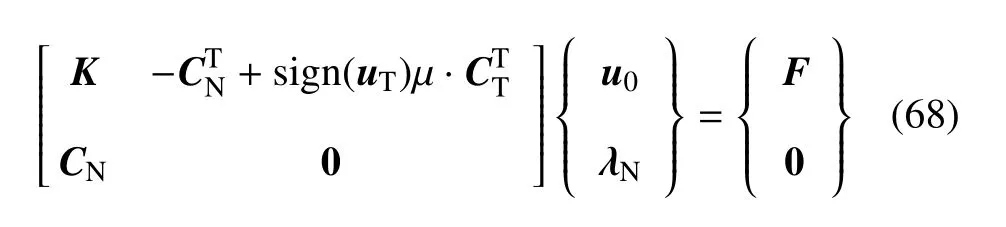
4 数值算例
4.1 贯穿裂纹板接触
图5为含贯穿裂纹的矩形板,板左端固定,右端受到q=100Pa的均匀压应力.板长3m,宽为2m,裂纹面与x轴夹角α=50◦,裂纹与上边界的交点坐标为(1.9m,2m).杨氏模量E=76kPa,泊松比ν=0.3,采用平面应变假设.假设斜裂纹摩擦系数f足够大,裂纹面处于完全粘结接触状态.采用多边形单元[34-35]进行离散.由于结构比较简单,因此将模型划分成2个子域,并采用2节点单元离散子域的边界(节点用•表示),如图6所示.由于是完全贯穿的裂纹,只需在裂纹面上采用点对点约束即可模拟接触问题.
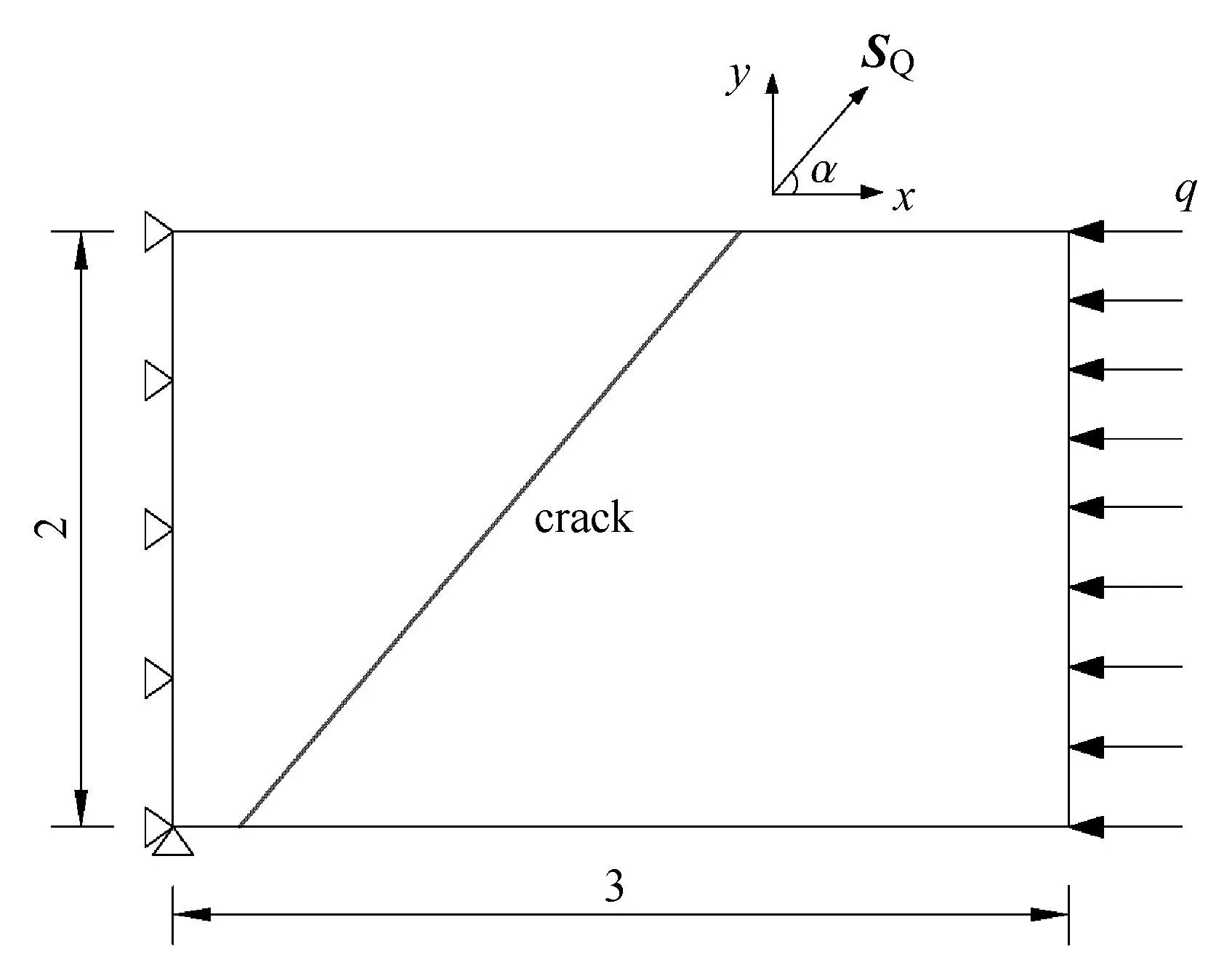
图5 含贯穿裂纹的矩形板(m)Fig.5 A rectangular plate divided by through crack(m)
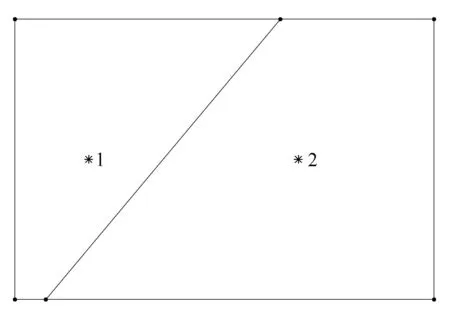
图6 多边形比例边界有限元网格Fig.6 Polygon SBFEM mesh
图7为板受压变形后的位移云图.由于裂纹面接触条件的施加,从位移云图中可看出,位移具有连续性,在受压裂纹面上没有发生相互嵌入,从而表明接触条件施加是正确的.
为了验证该方法精确性与收敛性,采用结构应变能相对误差作为指标.应变能误差的表达式[36]可以写为应变能的相对误差为
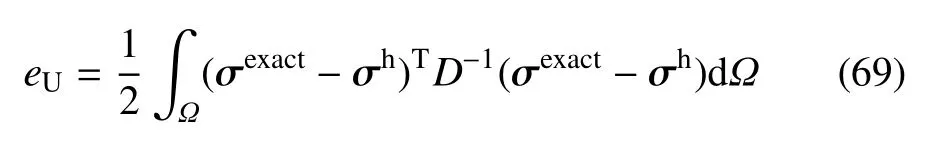
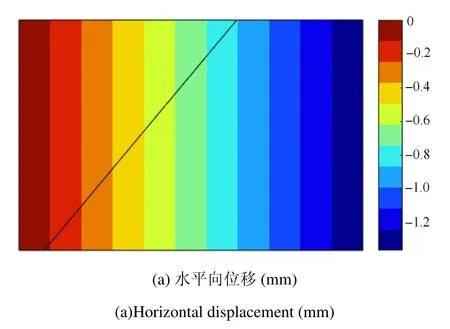
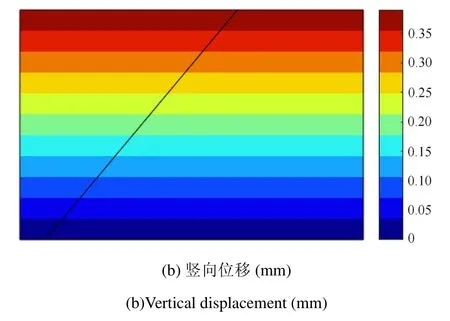
图7 位移云图Fig.7 Displacement fi eld

其中,σh是本文方法求得的应力,σexact为应力值解析解,Uexact为应变能解析解.
为了比较SBFEM求解裂纹面接触问题的精度和效率,采用目前应用较为广泛的商业有限元软件ABAQUS进行模拟对比.ABAQUS在接触程序处理中,采用Lagrange乘子接触[37].图8分别给出了两种方法计算得到的应变能相对误差随不同网格(粗网格、中等网格和细网格)的自由度变化,从图中可看出,SBFEM方法求解裂纹面接触问题收敛极快,仅需16个自由度就无限趋近于解析解(应变能相对误差为(3×10−20)%),随着网格的变化,求解精度基本不变.而ABAQUS收敛性较慢(粗网格下应变能相对误差(3.6×10−3)%),而且在网格较细,自由度较高的情况下,其计算精度仍远低于SBFEM较低的自由度计算精度,这说明了SBFEM求解裂纹面接触问题的高精度与高效性.
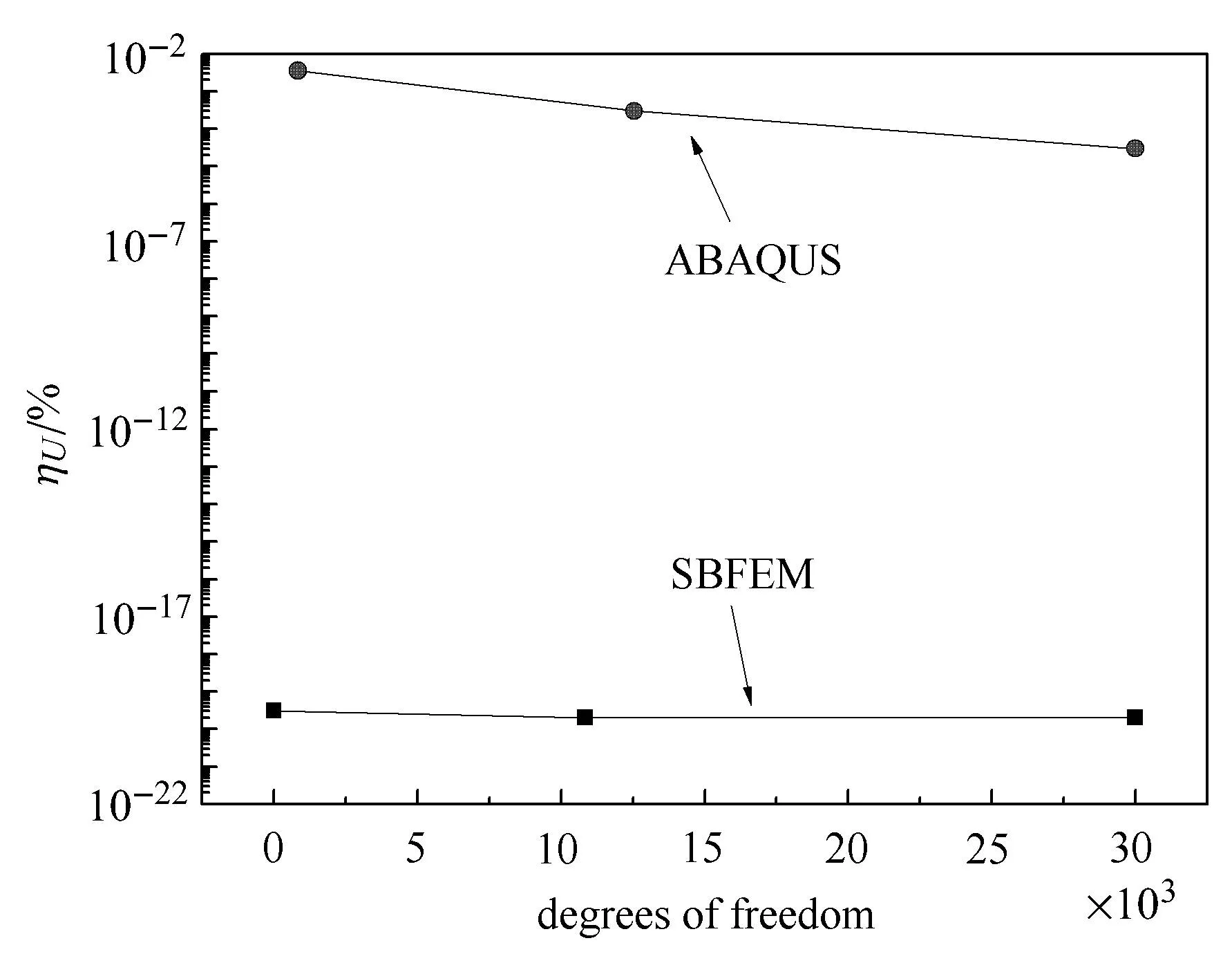
图8 应变能相对误差随网格自由度变化Fig.8 The relative error in the strain energy varies with the grid degrees of freedom
4.2 含有圆孔的缝内为非均匀压力的裂纹板接触
为了进一步验证该方法在一般情况下的求解能力,本文对含有孔洞及裂纹的无限大板在压力状态下进行了数值模拟.式(71)∼式(73)给出了含有半圆孔的半无限大板承受压力载荷时的解析解[38].该板在极坐标下的解为
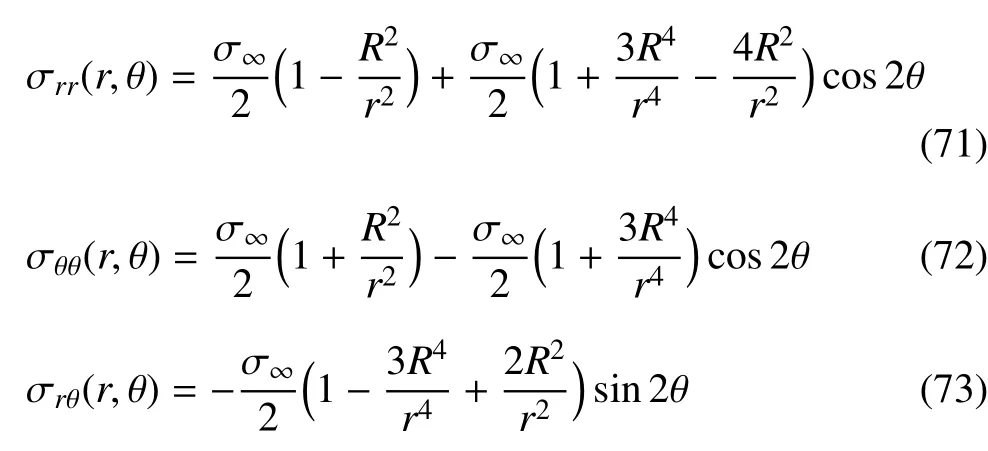
当板的尺寸长度L与圆孔半径R的比例足够大时,可以近似用来模拟含有半孔洞的无限大板.图9为该模型的几何尺寸.坐标系原点设在圆孔的圆心处,板的长度为30m,板的高度为15m,圆孔的半径R为1m,在圆孔的正下方有一条长度为a=1.68m的裂纹,板的两端受到σ∞=100Pa的均匀压力,板的上端数值方向位移为0.假设摩擦因子f足够大,裂纹处于完全粘结接触状态.
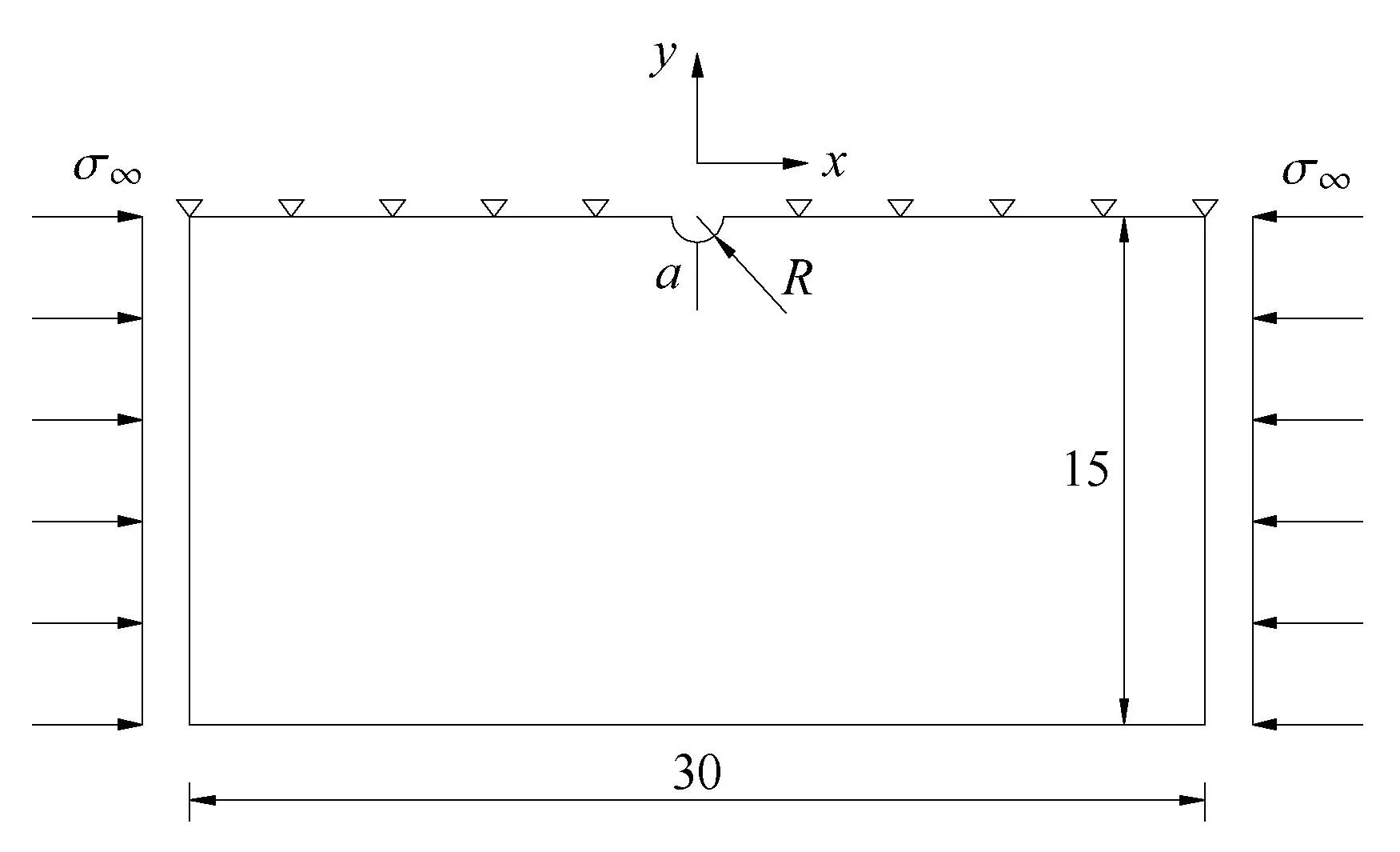
图9 包含有裂缝及圆孔的矩形板(m)Fig.9 Model of a rectangular plate with a crack and a circular hole(m)
板在孔洞周围存在应力集中现象,因此该模型采用较密的多边形网格进行离散,如图10所示(图中*为裂纹尖端).采用点对点与边对边接触方法求解该裂纹接触问题.
图11和图 12给出了结构的变形图和位移云图,由于原结构变形极小,图11对原结构变形进行了一定比例的放大(放大了70倍).从结构的变形图和位移云图可看出,采用该方法考虑接触时,变形与没有裂纹情况几乎一样,受压裂纹面上位移具有连续性,没有发生相互嵌入.从而表明接触算法是正确的.
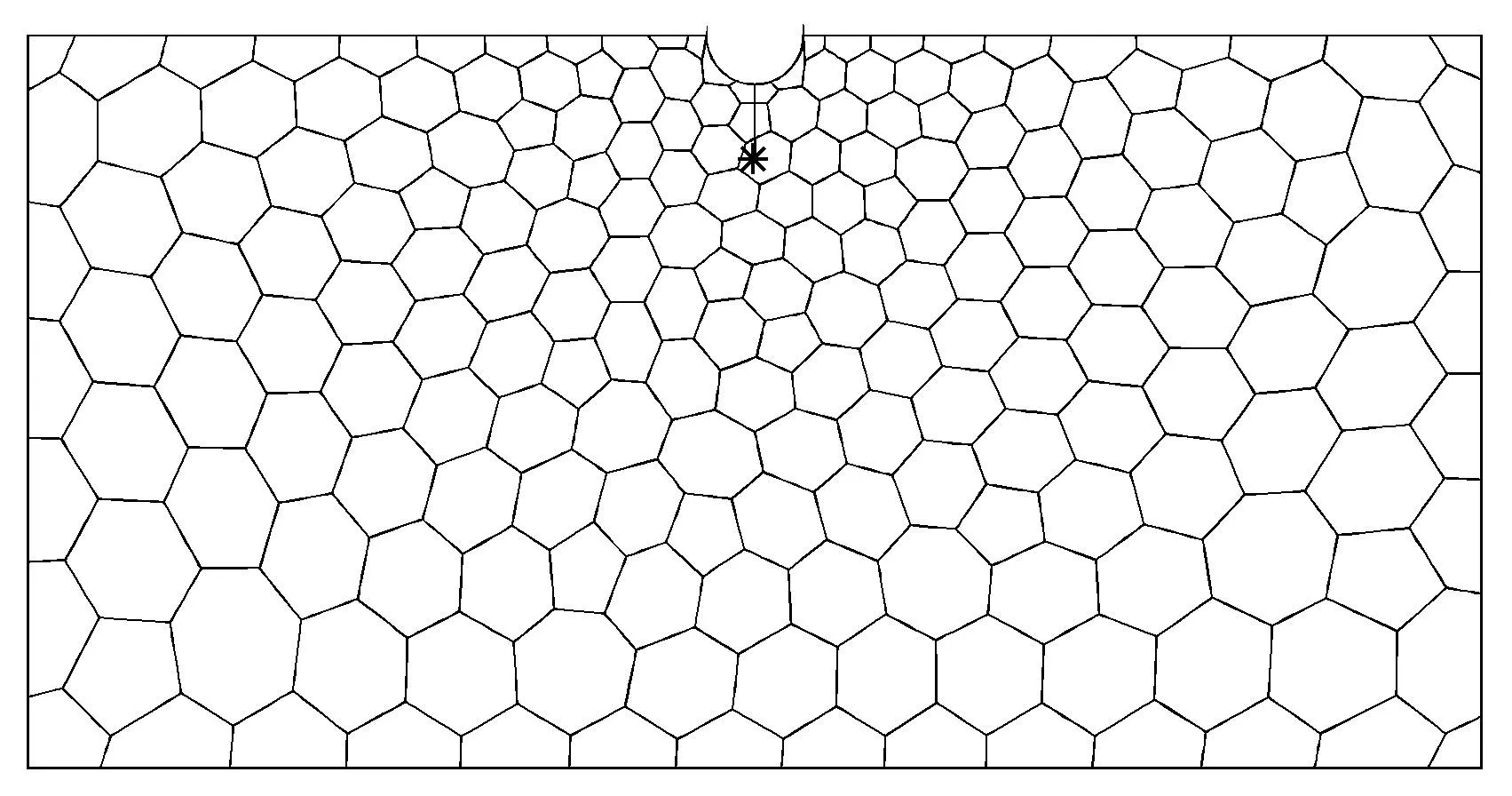
图10 包含有裂缝及圆孔的矩形板多边形网格Fig.10 Polygon SBFEM mesh of a rectangular plate with a crack and a circular hole
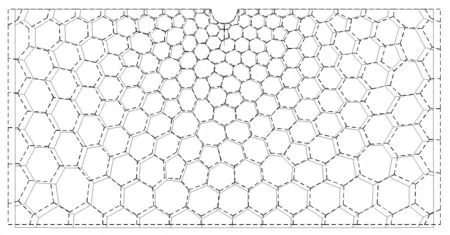
图11 结构变形图(放大70倍,虚线为未变形图)Fig.11 Structural deformation diagram(magni fi ed 70 times,dashed line is the original shape)
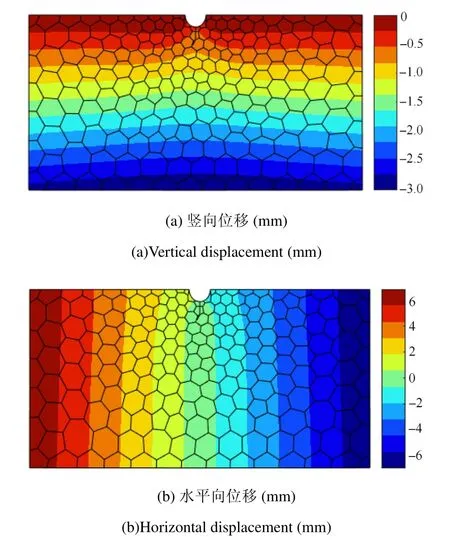
图12 位移云图Fig.12 Displacement fi eld
图13为采用SBFEM和ABAQUS两种方法计算的应变能相对误差随不同网格自由度的变化.由图中可看出,基于SBFEM求解的结果在自由度数较小情况下,误差较小(相对误差为0.0032%),而基于ABAQUS的求解误差在自由度数较小情况下所得误差较大(相对误差为1.7%),随着网格的加密,自由度数的增大,误差逐渐减小,但ABAQUS求解精度远小于SBFEM求解精度.这说明SBFEM点对点和边对边约束方法在非均布应力下的裂纹接触仍具有较高的精度和效率.
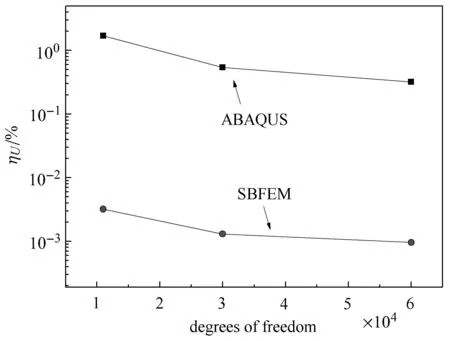
图13 应变能相对误差随网格自由度变化Fig.13 The relative error in the strain energy varies with the grid degrees of freedom
4.3 考虑摩擦的滑移接触
在满足粘结接触下,裂纹接触面在法向和切向方向都无相对位移.在有摩擦的滑移接触下,接触在法向方向仍然满足不嵌入条件,在切向方向,发生相互移动,系统方程满足式(68).为了验证SBFEM滑移接触的有效性,本文对一个含有裂纹尖端的矩形板进行了模拟,图14为该矩形板的多边形网格,其中裂尖坐标为(0.809m,0.7m),摩擦系数f=0.2,裂纹在切向上发生了滑移.其他力学参数与算例4.1中参数相同.
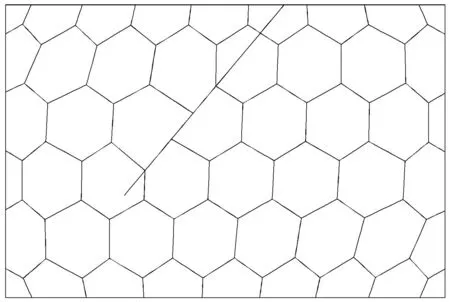
图14 多边形比例边界有限元网格Fig.14 Polygon SBFEM mesh
在裂纹接触面上产生滑移,两个接触面产生不连续位移,故图14采用了相对较多的多边形SBFEM网格对矩形板进行离散.图15和图16分别为矩形板变形图和位移云图,由图15中可看到,切向上产生了滑移,在法向上裂纹面间没有相互侵入.从而表明该滑移接触算法是正确的.
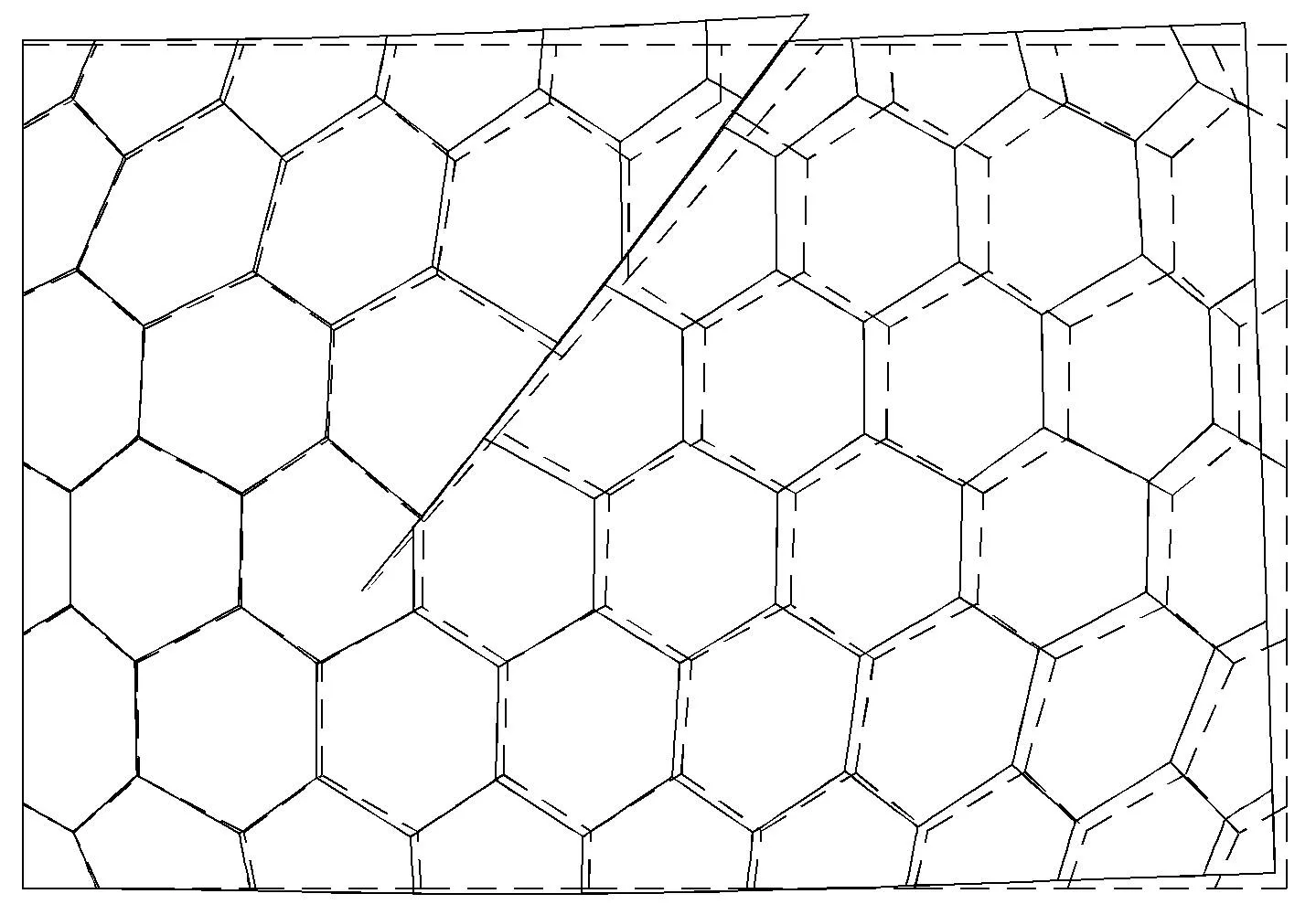
图15 结构变形图(放大30倍,虚线为未变形图)Fig.15 Structural deformation diagram(magni fi ed 30 times,dashed line is the original shape)
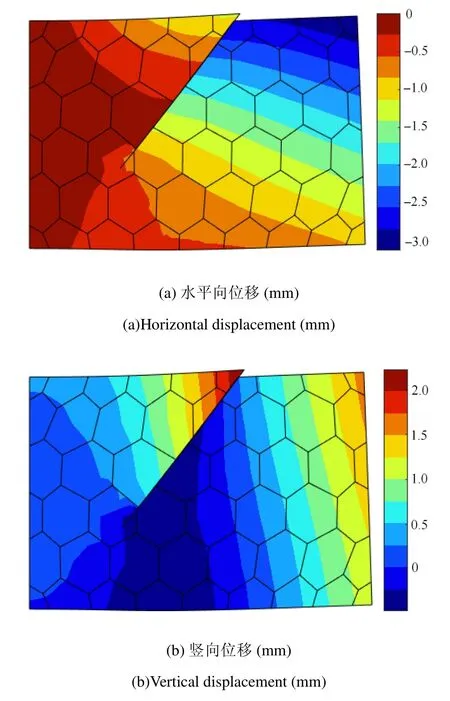
图16 位移云图Fig.16 Displacement fi eld
本算例没有解析解,仍采用商业有限元软件ABAQUS模拟结果来对比本文提出的SBFEM求解裂纹面接触方法的精度和效率.在使用ABAQUS模拟过程中,分别采用粗网格、中等网格和细网格求解该滑移接触问题,图17分别给出了ABAQUS不同网格的模型.

图17 ABAQUS不同网格模型Fig.17 Di ff erent mesh models of ABAQUS
图18为采用不同模型模拟得到的裂纹面下表面σxx分布,可看出在ABAQUS粗网格下,其应力分布与细网格相差较大,特别是靠近裂纹接触的两端,其应力误差较为明显,同时可看出SBFEM模拟结果与细网格的模拟结果较为一致.从网格对比来看,采用SBFEM求解的网格自由度数(数量为1560)远小于ABAQUS细网格的自由度数(数量为16325),SBFEM仅需较低的自由度即可达到较高精度的解.说明了本文SBFEM模型计算考虑摩擦的滑移接触的精确性与高效性.
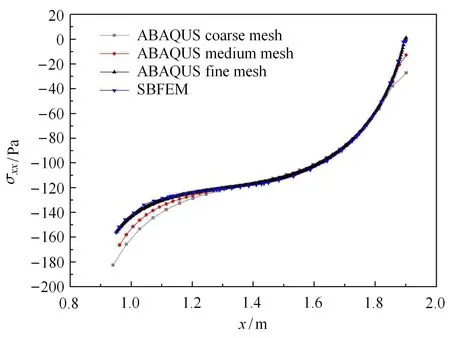
图18 裂纹面下表面σxx分布Fig.18 Stress σxxdistribution along right crack face
5 结论
本文基于比例边界有限元法,推导给出了侧面在任意载荷下的比例边界有限元的新型形函数,以及相应的SBFEM有关公式.运用Lagrange乘子法,推导给出了点对点与边对边接触的SBFEM求解裂纹面接触问题的支配方程,较为精确地模拟了裂纹面的接触,解决了裂纹面在受压时的粘接接触和滑移接触问题.通过3个算例的数值分析,验证了本文方法的精确性与高效性.算例表明,本文推导的考虑侧边载荷存在的SBFEM形函数是合适的;在不含有裂尖单元的裂纹面接触时,采用点对点接触模型即可精确地模拟裂纹面的接触条件;在含有裂尖单元的裂纹面接触时,需要对裂尖单元的侧面采用边对边约束接触模型.
1 嵇醒.断裂力学判据的评述.力学学报,2016,48(4):741-753(Ji Xing.A critical review on criteria of fracture mechanics.Chinese Journal of Theoretical and Applied Mechanics,2016,48(4):741-753(in Chinese))
2 李卧东,陈胜宏.接触摩擦问题的数值模拟.岩土力学,2003,24(3):385-388(Li Wodong,Chen Shenghong.Numerical model-ing for frictional contact problems.Rock and Soil Mechanics,2003,24(3):385-388(in Chinese))
3 高志强,傅卫平,王雯等.弹塑性微凸体侧向接触相互作用能耗.力学学报,2017,49(4):858-869(Gao Zhiqiang,Fu Weiping,Wang Wen,et al.Study on the contact energy dissipation of the lateraland interactional between the elastic-plastic asperities.Chinese Journal of Theoretical and Applied Mechanics,2017,49(4):858-869(in Chinese))
4 Tur M,Fuenmayor FJ,Wriggers P.A mortar-based frictional contact formulation for large deformations using Lagrange multipliers.Computer Methods in Applied Mechanics and Engineering,2009,198(37):2860-2873
5 MateiA.WeaksolvabilityviaLagrangemultipliersforcontactproblems involving multi-contact zones.Mathematics and Mechanics of Solids,2016,21(7):826-841
6 Hansbo P,Rashid A,Salomonsson K.Least-squares stabilized augmented Lagrangian multiplier method for elastic contact.Finite Elements in Analysis and Design,2016,116(1):32-37
7 Benkhira EH,Essou fiEH,Fakhar R.On convergence of the penalty method for a static unilateral contact problem with nonlocal friction in electro-elasticity.European Journal of Applied Mathematics,2016,27(1):1-22
8 Bourichi S,Essou fi E.Penalty method for unilateral contact problem with Coulomb’s friction for locking material.International Journal of Mathematical Modelling&Computations,2016,6(1):61-81
9 李建宇,潘少华,张洪武.解三维摩擦接触问题的一个二阶锥线性互补法.力学学报,2009,41(6):869-877(Li Jianyu,Pan Shaohua,Zhang Hongwu.A second-order cone linear complementarity approach for three-dimensional frictional contact problems.Chinese Journal of Theoretical and Applied Mechanics,2009,41(6):869-877(in Chinese))
10 Song C,Wolf JP.The scaled boundary fi nite-element method—alias consistent in fi nitesimal fi nite-element cell method—for elastodynamics.Computer Methods in Applied Mechanics and Engineering,1997,147(3):329-355
11 Deeks AJ,Wolf JP.A virtual work derivation of the scaled boundary finite-element method for elastostatics.Computational Mechanics,2002,28(6):489-504
12 Song C,Wolf JP.Semi-analytical representation of stress singularities as occurring in cracks in anisotropic multi-materials with the scaled boundary fi nite-element method.Computers&Structures,2002,80(2):183-197
13 Birk C,Prempramote S,Song C.An improved continued-fractionbased high-order transmitting boundary for time-domain analyses in unbounded domains.International Journal for Numerical Methods in Engineering,2012,89(3):269-298
14 Saputra A,Talebi H,Tran D,et al.Automatic image-based stress analysisbythescaledboundary fi niteelementmethod.International Journal for Numerical Methods in Engineering,2017,109(5):697-738
15 Behnke R,Mundil M,Birk C,et al.A physically and geometrically nonlinear scaled-boundary-based fi nite element formulation for fracture in elastomers.International Journal for Numerical Methods in Engineering,2014,99(13):966-999
16 吴泽艳,王立峰,武哲.比例边界坐标插值方法在谱元法中的应用——无穷域Euler方程的数值模拟.力学学报,2013,45(4):619-623(Wu Zeyan,Wang Lifeng,Wu Zhe.The scaled boundary coordinate interpolation method and its application to spectral element method:numerical simulation of the Euler equations over unbounded domains.Chinese Journal of Theoretical and Applied Mechanics,2013,45(4):619-623(in Chinese))
17 薛冰寒,林皋,胡志强等.摩擦接触问题的比例边界等几何B可微方程组方法.力学学报,2016,48(3):615-623(Xue Binghan,Lin Gao,Hu Zhiqiang,et al.Analysis of frictional contact problems by SBIGA-BDE method.Chinese Journal of Theoretical and Applied Mechanics,2016,48(3):615-623(in Chinese))
18 陈灯红,杜成斌.基于SBFE和改进连分式的有限域动力分析.力学学报,2013,45(2):297-301(Chen Denghong,Du Chengbin.Dynamic analysis of bounded domains by SBFE and the improved continued-fraction expansion.Chinese Journal of Theoretical and Applied Mechanics,2013,45(2):297-301(in Chinese))
19 Ooi ET,Song C,Tin-Loi F.A scaled boundary polygon formulation for elasto-plastic analyses.Computer Methods in Applied Mechanics and Engineering,2014,268(1):905-937
20 Zheng Z,Zang M,Chen S,et al.An improved 3D DEM-FEM contact detection algorithm for the interaction simulations between particles and structures.Powder Technology,2017,305(1):308-322
21 王福军,王利萍,程建钢等.并行有限元计算中的接触算法.力学学报,2007,39(3):422-427(Wang Fujun,Wang Liping,Cheng Jianggang,et al.A contact algorithm for parallel computation of FEM.Chinese Journal of Theoretical and Applied Mechanics,2007,39(3):422-427(in Chinese))
22 Giner E,Tur M,Taranc´on JE,et al.Crack face contact in X-FEM usingasegment-to-segmentapproach.InternationalJournalforNumerical Methods in Engineering,2010,82(11):1424-1449
23 Zheng A,Luo X.A mathematical programming approach for frictional contact problems with the extended fi nite element method.Archive of Applied Mechanics,2016,86(4):599-616
24 刘永健,姚振汉.三维弹性体移动接触边界元法的一类新方案.工程力学,2005,22(1):6-11(Liu Yongjian,Yao Zhenhan.A new scheme of BEM for moving contact of 3D elastic solid.Engineering Mechanics,2005,22(1):6-11(in Chinese))
25 Yang ZJ,Deeks AJ.Fully-automatic modelling of cohesive crack growth using a fi nite element–scaled boundary fi nite element coupled method.Engineering Fracture Mechanics,2007,74(16):2547-2573
26 钟红,宋平平.任意裂纹面载荷作用下界面断裂分析.哈尔滨工业大学学报,2016,48(2):152-157(Zhong Hong,Song Pingping.Analysis of interface crack with arbitrary crack tractions.Journal of Harbin Institute of Technology,2016,48(2):152-157(in Chinese))
27 Song C.A super-element for crack analysis in the time domain.International Journal for Numerical Methods in Engineering,2004,61(8):1332-1357
28 Deeks AJ,Wolf JP.Semi-analytical elastostatic analysis of unbounded two-dimensional domains.International Journal for Numerical and Analytical Methods in Geomechanics,2002,26(11):1031-1057
29 Song C.A matrix function solution for the scaled boundary fi niteelement equation in statics.Computer Methods in Applied Mechanics and Engineering,2004,193(23):2325-2356
30 Vu TH,Deeks AJ.Use of higher-order shape functions in the scaled boundary fi nite element method.International Journal for Numerical Methods in Engineering,2006,65(10):1714-1739
31 Ooi ET,Song C,Natarajan S.Construction of high-order complete scaled boundary shape functions over arbitrary polygons with bubble functions.International Journal for Numerical Methods in Engineering,2016,108(9):1086-1120
32 宣兆成,李兴斯.接触分析的光滑模型及迭代算法.力学学报,2001,33(3):340-348(Xuan Zhaocheng,Li Xingsi.Smooth model and iteration algorithm for contact analysis.Acta Mechanica Sinica,2001,33(3):340-348(in Chinese))
33 王勖成.有限单元法.北京:清华大学出版社,2013(Wang Xucheng.Finite Element Method.Beijing:Tsinghua University Press,2013(in Chinese))
34 Dai S,Augarde C,Du C,et al.A fully automatic polygon scaled boundary fi nite element method for modelling crack propagation.Engineering Fracture Mechanics,2015,133(1):163-178
35 Ooi ET,Song C,Tin-Loi F,et al.Polygon scaled boundary fi nite elements for crack propagation modelling.International Journal for Numerical Methods in Engineering,2012,91(3):319-342
36 Deeks AJ,Augarde CE.A meshless local Petrov-Galerkin scaled boundary method.Computational Mechanics,2005,36(3):159-170
37 庄茁.基于ABAQUS的有限元分析和应用.北京:清华大学出版社,2008(Zhuang Zhuo.Based on ABAQUS Finite Element Analysis and Application.Beijing:Tsinghua University Press,2008(in Chinese))
38 徐芝纶.弹性力学.北京:高等教育出版社,2006(XuZhilun.Elasticity.Beijing:Higher Education Press,2006(in Chinese))
CRACK FACE CONTACT PROBLEM ANALYSIS USING THE SCALED BOUNDARY FINITE ELEMENT METHOD1)
Zhang Peng Du Chengbin2)Jiang Shouyan
(Department of Engineering Mechanics,Hohai University,Nanjing211100,China)
In the case of arbitrary tractions on the side faces of the crack,a polynomial function of the radial coordinate can be employed to describe the side face loads in the scaled boundary fi nite element method(SBFEM).The SBFEM new shape function considering the side face loads is presented.The corresponding sti ff ness matrix and equivalent node load is derived together based on the SBFEM new shape function.The model of crack face contact using the SBFEM is proposed in this paper for the fi rst time.Lagrange’s multiplier method is used to establish the contact constraints of contact model between crack faces.The governing equations for the nonlinear surface contact problems in SBFEM is derived,including adhesion contact problems and sliding friction problems.The elements where the crack faces lie are divided into non crack tip elements and the crack tip element.For the former,the crack faces act as the boundary of the SBFEM element,the contact tractions on the boundary can be assigned to the nodes equivalently and the Lagrange’s multiplier is applied for the point constraints.For the latter,the interpolation fi eld of Lagrange’s multiplier is constructed on the whole side faces.The Lagrange’s multiplier is assumed to be linear along the side faces,the segment constraint approach is proposed to optimize the ful fi lment of the contact constraints along the crack faces.By comparing the results of the calculation of analytical solution and software ABAQUS on three di ff erent numerical contact problems of crack faces,the accuracy and e ff ectiveness of the proposed point-to-point and segment-to-segment contact model for fracture surfaces contact problems is veri fi ed in this paper.
scaled boundary fi nite element method,shape functions,crack,point constraints,segment constraints
O346.1
A doi:10.6052/0459-1879-17-195
2017–05–23 收稿,2017–08–07 录用,2017–08–11 网络版发表.
1)国家自然科学基金资助项目(11372098,51579084,51309088).
2)杜成斌,教授,主要研究方向:水工结构工程中的力学问题.E-mail:cbdu@hhu.edu.cn.
章鹏,杜成斌,江守燕.比例边界有限元法求解裂纹面接触问题.力学学报,2017,49(6):1335-1347
Zhang Peng,Du Chengbin,Jiang Shouyan.Crack face contact problem analysis using the scaled boundary fi nite element method.Chinese Journal of Theoretical and Applied Mechanics,2017,49(6):1335-1347
