花生分段收获挖掘铲力学模型及试验分析

王 冰，胡志超，周德欢，彭宝良，陈友庆

(农业部南京农业机械化研究所，南京 210014)



花生分段收获挖掘铲力学模型及试验分析

王 冰，胡志超，周德欢，彭宝良，陈友庆

(农业部南京农业机械化研究所，南京 210014)

为优化花生收获挖掘铲的结构参数，对花生收获挖掘铲进行受力分析，并建立工作状态的力学模型，研究各个参数的变化对受力状况的影响，找出对工作阻力具有影响的参数和薄弱部位。通过田间试验，对力学模型进行验证，结果表明：影响工作阻力的参数有犁面与地面的夹角、犁面的开度角、前失效角的倾角及土壤重力，犁柱截面C为薄弱部位，力学模型与收获挖掘铲的受力状况基本相符。

花生；分段收获；挖掘铲；数学模型

0 引言

我国花生种植面积约467万hm2，在平原、坝区、丘陵、山地皆有种植，种植土壤为砂土、砂壤土、壤土、粘土等。花生有分段式和联合式两种机械化收获方式：分段收获方式由不同装备分别完成花生起秧、摘果等作业，一般先用带有挖掘铲的花生收获机或挖掘犁起秧，经晾晒再用捡拾联合收获机捡拾摘果或摘果机场上摘果；联合收获方式是通过花生联合收获机完成挖掘、清土、摘果、清选及集果等作业，可一次性完成整个花生收获机械化作业，是集成度最高的花生机械化收获技术[1]。我国大陆花生收获主要还依靠人工，部分地区使用挖掘犁收获机挖掘花生，同时在花生收获机上增加抖土、铺放等功能，以便于花生秧蔓进行晾晒[2-3]，花生联合收获方式也在逐步推广当中。花生收获挖掘犁可在砂土、壤土、黏重土壤区作业，具有结构简单、配套动力小、低成本及便于维护等优点；但分段收获模式下的收获机的堵塞、缠绕、损失率高、适应性差等问题比较突出[3-8]。

挖掘铲是花生挖掘收获机的关键部件，其结构参数和受力状况决定了收获机作业效果及工作性能的好坏。用于花生收获的挖掘铲有诸多类型，本文主要针对农业部南京农业机械化研究所研制的花生收获挖掘铲的结构和受力状况进行分析，建立花生收获挖掘铲工作阻力模型，找出薄弱环节，通过确定作业参数和优化结构参数，进而为提高花生收获机的性能和指标提供理论研究基础。

1 挖掘铲的结构特点和工作过程

该机挖掘铲主要由犁面、犁柱、调节机构、U型连接板等组成，如图1所示。挖掘铲收获作业时，挖掘铲犁面将土壤翻起，对土壤进行挤压，实现花生与土壤的分离。其漏挖率低，尤其适合土壤与花生难以分离的粘重土壤区作业。

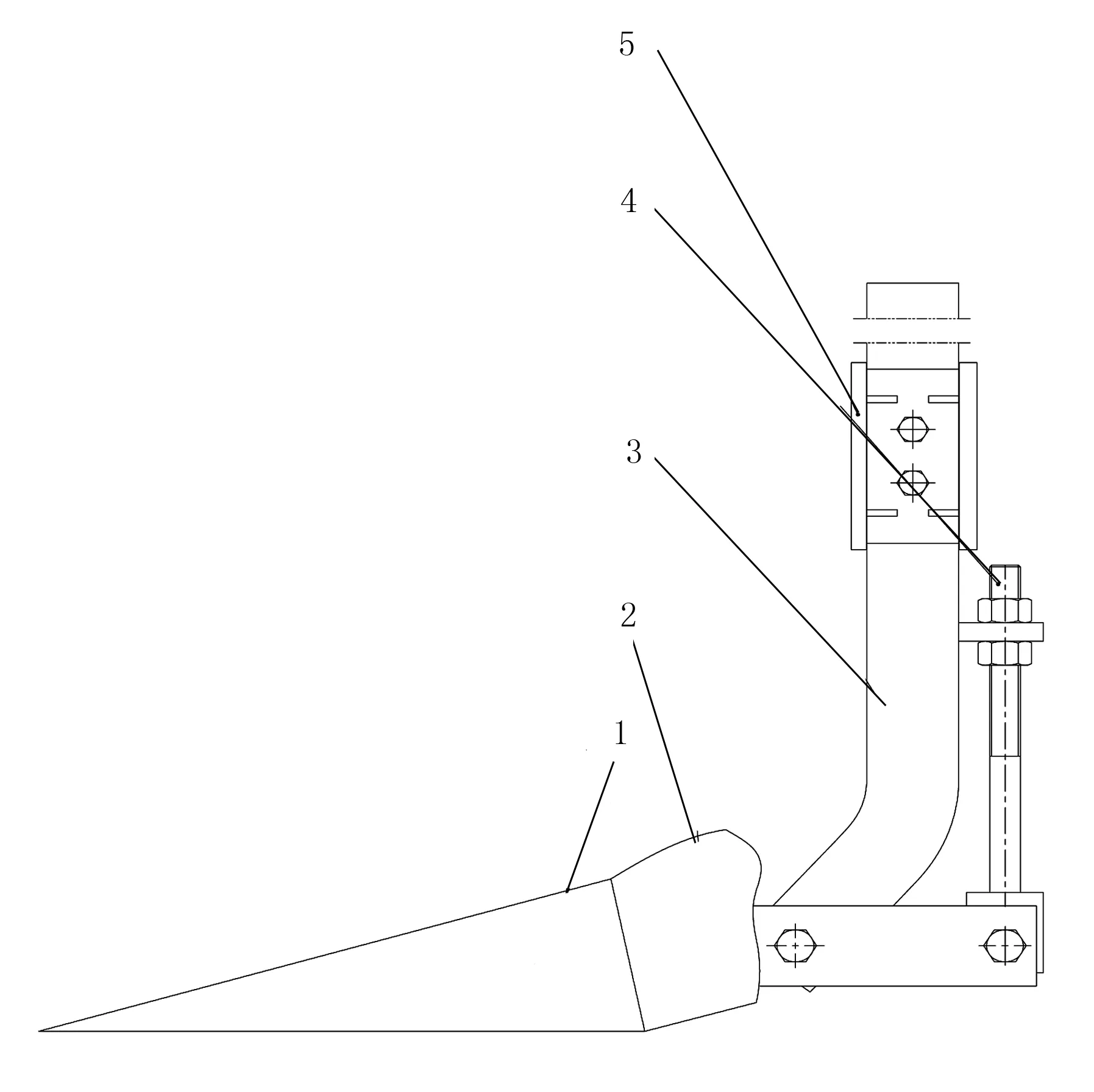
1.犁面 2.犁面 3.犁柱 4.调节机构 5. U型连接板

挖掘铲犁面采用“人”字型一体式设计，犁面后侧弯曲角度大于前侧，土壤沿犁面进行翻转，减少埋果损失；设计有入土角调节机构，可根据不同地况来调整入土角。

2 挖掘铲的受力分析与建模

根据挖掘铲的收获机理，挖掘铲的工作阻力F可以看作由挖掘铲犁面1所受力F1、犁面2所受力F2和立柱的受力F3这3部分构成，即F=F1+F2+F3。

2.1 犁面受力分析与建模

通常犁体会以一定角度切入土壤，垄体中作用在犁体上的力主要分为切削阻力、牵引阻力、摩擦阻力及土壤重力形成的法向载荷。对犁体的犁面进行受力分析[9-10]，建立平衡方程，通过整理可得

N11=N1sinα2+μN1cosα2

(1)

F1=N11sinβ1

=N1sinα1sinβ2+μN1cosα1sinβ1+kb1

(2)

其中，N11为作用到犁面1上的力向地面的投影力；N1为作用到犁面1的法向载荷；α1为犁面1与地面的夹角；F1为犁面1所受的水平阻力；β1为犁面1的开度角；μ为犁面与土壤的摩擦系数；k为单位幅宽土壤的纯切削阻力；b1为犁面1宽度。

图2所示为犁面1受力分析，图3所示为犁面2受力分析。

图2 犁面1受力分析

图3 犁面2受力分析

建立平衡方程并整理可得

N21=N2sinα2+μN2cosα2

(3)

F2=N21sinβ2

=N2sinα2sinβ2+μN2cosα2sinβ2+kb2

(4)

其中，N21为作用到犁面2上的力向地面的投影力；N2为作用到犁面2的法向载荷；α2为犁面2与地面的夹角；F2为犁面2所受的水平阻力；β2为犁面2的开度角；μ为犁面与土壤的摩擦系数；k为单位幅宽土壤的纯切削阻力；b2为犁壁2宽度。

一般情况下，花生种植地土壤粘度适中，无大的石块，犁体切削土壤所受的纯切削阻力很小，可忽略不计，因此可得犁体犁面的受力F1和F2分别为

F1=N1sinα1sinβ1+μN1cosα1sinβ1

(5)

F2=N2sinα2sinβ2+μN2cosα2sinβ2

(6)

式(5)和(6)两项内容分别包括法向力N1和N2，挖掘铲犁体主要受到土壤的反作用力。图4和图5是工作时土块被犁面铲起的受力分析[11-12]，分别在垂直和水平方向上建立力平衡方程。为了更容易理解，进一步简化，记t1=C1S1+B1，t2=C2S2+B2，方向分别与μ1N3和μ2N4相同，则

G1-N1(cosα1-μsinα1)-

N3(cosδ1-μ1sinδ1)+t1sinδ1=0

(7)

N1(sinα1+μcosα1)-N3(sinδ2+

μ1cosδ1)-t1cosδ1=0

(8)

其中，G1为作用于犁面1的土壤块重力；μ1为土壤之间摩擦因数；N3为作用于前侧的垂直载荷；δ1为前失效角的倾角；S1为前剪切失效面的面积；C1为土壤自身性能决定的土壤内聚力；B1为土壤加速力。

记t=CS+B，指剪切过程中内聚力和加速力对土壤综合作用力，B=mdv/dt。其中，m为加速土壤的质量，t为加速时间。则

G2-N2(cosα2-μsinα2)-

N4(cosδ2-μ2sinδ2)+t2sinδ2=0

(9)

N2(sinα2+μcosα2)-N4(sinδ2+μ2cosδ2)-

t2cosδ2=0

(10)

其中，G2为作用于犁面2的土壤块重力；μ2为土壤之间的摩擦因数；N4为作用于前侧的垂直载荷；δ2为前失效角的倾角；S2为前剪切失效面的面积；C2为土壤自身性能决定的土壤内聚力；B2为土壤加速力。

将方程联立，分别消去N1、N3和N2、N4，经过整理可得

(11)

(12)

2.2 犁柱受力分析与建模

犁柱的上端用固定座紧固于机架上，使挖掘铲对机架既不能有相对移动，也不能有相对转动，可将此固定座简化为固定端支座，即固定端；作用在铲柄上的力主要分布在下端，来自于犁体的阻力，其分布范围远小于铲柄的长度，可简化为集中力。因此，可将铲柄简化为矩形截面悬臂梁，其受力如图6所示。悬臂梁的固定端受垂直反力FRA和反作用力偶MA作用。由平衡方程∑Fy=0,∑MA=0，求得FRA=F1+F2，MA=(F1+F2)L,选取坐标系如图6所示。在距原点为x的横截面左侧，有支反力FA、MA，而在截面的右侧，载荷均布；所以用截面右侧的外力来计算剪力和弯矩较为合理。计算F3和M为：F3=F1+F2，M(x)=(F1+F2)×(L-x)，绘出剪力、弯矩图如图6所示。

由图6可看出：最大弯矩在截面C上，且Mmax=(F1+F2)L。由分析可知，犁柱截面C处为薄弱环节。

图6 犁柱的剪力和弯矩

3 试验验证与结果分析

3.1 试验目的

理论上，挖掘铲的相关数据计算值是通过测定挖掘铲实际作业过程中参数并结合建立的数学模型得到的；另外，还需测定挖掘铲田间作业时的实际受力状况试验值；最后，通过比较和分析理论数据和试验测到的实际受力数据，检验刚建立数学模型是否能够反应挖掘铲的实际受力状况。

3.2 试验条件和装置

试验选取南京有代表性的丘陵薄地，地点是南京六合花生种植区域，土质为粘土。作业机的驱动动力使用了黄海金马254A拖拉机，挖掘铲部件为本文所设计的双翼式挖掘铲，其他测试设备包括阻力传感器、卷尺、直尺及秒表等。

3.3 试验方法

取长140m、宽60m的平坦地面作为试验用地，并规定前20m为入土非稳定区，后20m为出土非稳定区，以保证试验的稳定性和可靠性，中间100m为试验测试区。设计两种挖掘深度(0.1m和0.2m)和两种作业速度(1.5km/h和3km/h)，通过进行交叉试验，得到4个测量值，用来验证上文建立的数学模型。

为了保证试验的准确性，消除可能的干扰因素产生的不利影响，反复进行多次试验，分别改变作业速度和挖掘深度，对结果进行分析处理，最终得到试验结果如表1所示。

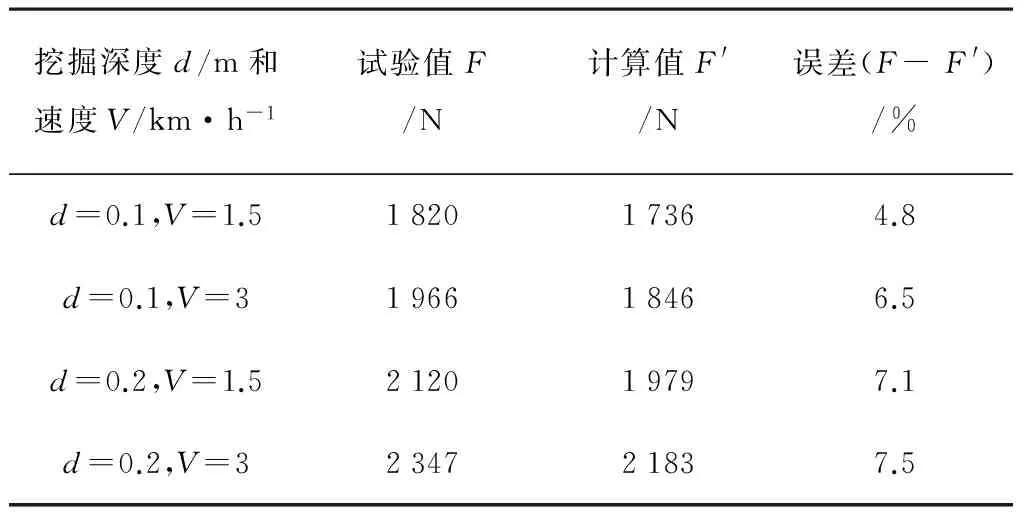
表1 试验结果

表1显示：当挖掘深度0.1m、作业速度1.5km/h时，实际测试阻力为1 820N，理论计算阻力为1 736N，两者相差4.8%；当挖掘深度0.1m、作业速度3km/h时，实际测试阻力为1 966N，理论计算阻力为1 846N，两者相差6.5%；当挖掘深度0.2m、作业速度3km/h时，实际测试阻力为2 347N，理论计算阻力为2 183N，两者相差7.5%。由此可以看出：误差在速度和深度相应增加时有所增大，且增大比例正相关。由于田间试验实际条件不易控制，并且土壤各参数的测定也存在一定误差，可以确定建立的数学模型基本能够反映实际工作过程的受力状况。

从建立模型的影响参数分析，影响参数为铲面与地面的夹角α、铲面的开度角β、前失效角的倾角δ、土壤重力G及截面C的结构尺寸。通过设计调整可以改变铲面与地面的夹角α、铲面的开度角β及截面C的结构尺寸，可以借助模拟分析优化其设计参数，得到挖掘铲作业性能最佳的结构参数。综合分析表明，试验结果对挖掘铲生产作业设定参数的调整有较好的指导作用。

4 结论

1)通过对挖掘铲进行受力分析，建立了挖掘铲受力数学模型：挖掘铲犁面1的受力模型为方程(11)，挖掘铲犁面2的受力模型为方程(12)；犁柱所受的剪力为Fs=F1+F2，犁柱所受弯矩为M(x)=(F1+F2)×(L-x)。

2)对比数学模型计算结果和田间试验测定结果，验证了计算值与挖掘铲田间工作过程的受力状况基本一致，但误差随挖掘铲的工作速度和挖掘深度增加而增大。这说明，该数学模型还要进一步完善和改进，以得出设计挖掘深度和机器前进速度的模型的准确参数。

3)对该数学模型各参数间关系进行分析表明，挖掘深度d、铲面与地面的夹角α、铲面的开度角β、前失效角的倾角δ、土壤重力G及铲柄截面C的结构尺寸对阻力均有影响。

[1] 胡志超.半喂入花生联合收获机关键技术研究[D].南京：南京农业大学，2011.

[2] 尚书旗，王方艳，刘曙光，等.花生收获机械的研究现状与发展趋势[J].农业工程学报，2004,20(1):20-25.

[3] 胡志超，王海鸥，彭宝良，等.国内外花生收获机械化现状与发展[J].中国农机化,2006(5):40-43.

[4] 尚书旗，王方艳，刘曙光.花生生产机械化的应用现状与进展分析[J].花生学报,2003(11):509-517.

[5] 程俊峰，张飞.河南省花生收获机应用现状分析[J].农业科技与装备,2010(8):68-70.

[6] 马建民，张飞，楚宜民.河南省花生收获机械现状研究[J].农业机械,2009(4):82-85.

[7] 郑月男，尚书旗，杨然兵，等.山东省花生种植和收获现状的研究[J].农业机械,2009(14):52-54.

[8] 滕美茹，田立忠，陈广成.花生收获机的现状与发展[J].农机化研究,2011,33(10):211-215.

[9] Harrison H P，licsko J Z.Soil reacting wrenches and dynamics for three models of bentleg plows[J].Transations of the ASAE,1989,32(1):50-53.

[10] 余泳昌，刘文艺，赵迎芳，等.立柱式深松铲受力数学模型及试验分析[J].农业工程学报,2007(6):109-113.

[11] Γ.H 西涅阿可夫，И.M潘诺夫.土壤耕作机械的理论和计算[M].北京：中国农业机械出版社,1981:689-694.

[12] Bandalan E P.Salokhe V M,Gupta C P,et al.Performance of an oscillating subsoiler in breaking a hardpan[J].Journal of terramechanics,1999,36(1):117-125.

Mechanical Model and Experimental Research of Peanut Harvest Digger Blade

Wang Bing， Hu Zhichao， Zhou Dehuan， Peng Baoliang， Chen Youqing

(Nanjing Institute of Agricultural Mechanization Ministry of Agriculture, Nanjing 210014, China)

For optimizingstructure parameters of peanut harvest digger blade，force analysis of peanut harvest digger blade was conducted，and mechanical model at working condition was established，influences of various parameters changes on force condition were studied, the influencing parameters and the weak parts of share shaft on working resistance were found out. In order to ensure the accuracy of the mathematical model and the reliability of the simulated results，the real field experiments were also carried out to confirm the established force mathematical model. The results proved that the parameters which affect the effective resistance were included angle between plough wall and ground，plough wall opening angle，the dip of front failure angle，soil gravity，share shaft section C is the weak position.The mathematical model could reflect the harvest digger blade’s real force conditions.

peanut; havest; digger blade； mathematical model

2016-08-26

中国农业科学院创新工程(2013-2015，2016-2020)；国家花生产业技术体系(CARS-14)

王 冰(1963-)，男，山东德州人，助理研究员，博士研究生，(E-mail)supbing@163.com。

胡志超(1963-)，男，陕西蓝田人，研究员，博士生导师，(E-mail)zchu369@163.com。

S225.7+3

A

1003-188X(2017)10-0058-05