片状体最小悬浮速度的计算模型

袁成宇，王 娟，陈致水，廖宇兰

(海南大学 机电工程学院，海口 570228)



片状体最小悬浮速度的计算模型

袁成宇，王 娟，陈致水，廖宇兰

(海南大学 机电工程学院，海口 570228)

片状体最小悬浮速度可通过传统理论计算和试验获取，因此提出了一种处于压差阻力状态下的片状体最小悬浮速度的计算模型。同时，以甘蔗叶为对象，通过自制的悬浮速度测试装置进行了测试。通过比较发现：传统理论计算的蔗叶最小悬浮速度与实测的最小悬浮速度相差较大，最大相对误差为97.3%，最小相对误差为39.4%；而采用本文提供的方法所得的计算结果与实测值的最大相对误差为24.9%，最小相对误差为4.75%。

片状物；最小悬浮速度；数学模型

0 引言

物料悬浮速度是指在垂直气流的作用下，物料所受气流作用力等于该物料本身的重力，而使其保持平衡状态时的气流速度，它是进行风选除杂及确定物料气力输送运动的主要依据。目前，获取物料悬浮速度的方法主要有理论计算与实验测量两种。对于比较规则的球体或类似球体物料，一般通过理论计算可以获得比较合理的结果；而对于与球体偏差较大或者不规则物料，一般通过体积当量球等理论可计算得出相应的悬浮速度。例如，须山启介等对谷粒在垂直气流中的悬浮速度，李学军等对茶叶的悬浮速度及在空气中的运动、周作伸等对羽毛在空气中的运动，干方建等对烟草在气流中的悬浮运动进行了理论分析，得出了相应的计算结果，但在分析过程中采用了近似处理，其结果可能与实际情况产生一定偏差，最终仍需通过试验方法加以修正。本文根据片状颗粒在垂直流场中的受力分析，给出了一种相对简单的悬浮速度计算模型，并通过自制的测试装置验证该模型计算结果与不规则片状体传统理论计算的悬浮速度的一致程度。

1 悬浮速度传统计算方法

目前，悬浮速度一般是根据物料在流场中的受力平衡进行计算的，即物料重力等于流动阻力和浮力之和。传统方法计算的公式表达为

(1)

其中，v为颗粒最小悬浮速度(m/s)；ρs为悬浮颗粒密度(kg/m3)；ρg为气流密度(kg/m3)；d为颗粒直径(m)；C为阻力系数；g为重力加速度(9.81N/kg)。当不规则颗粒处于压差阻力区时，C为常数取0.44，颗粒直径以体积当量直径代替，此时悬浮速度的计算公式为

(2)

其中，de为等体积当量直径，de=1.24(m/ρs)1/3，m为颗粒质量；K为形状影响系数。利用公式(2)可求出的颗粒的悬浮速度，但对片状体而言，由于其形状与球体存在很大差异，即使通过形状影响系数修正，其计算结果也可能存在较大偏差。

2 片状体最小悬浮速度计算模型

设有一均质片状颗粒在流速为u流场中的压差阻力区处于悬浮状态，其受力分析如图1所示。

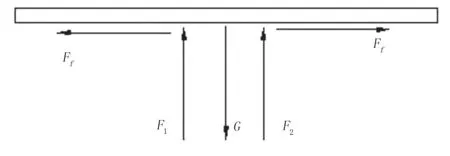
图1 叶片悬浮态受力分析

G=F1+F2

(3)

(4)

由贝努力方程可近似认为风速与风动压的关系为

(5)

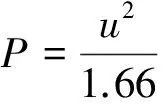
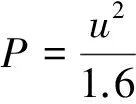
(6)

整理可得片状颗粒悬浮速度的公式为

(7 )

当悬浮片状物的密度ρs≫ρg时，则式(7)可以简化为

(8)

式(8)即为片状体最小悬浮速度计算的数学模型。其中，V为片状体的体积(m3)；S为迎流面积(m2)；ρs为悬浮颗粒密度(kg/m3)；m为质量(kg)。从公式(8)可知：片状体的最小悬浮速度不需要考虑体积当量直径和形状系数的影响，当均质片状体迎风面积相同时，最小悬浮速度仅与质量m有关。

3 试验验证

为验证公式(8)的合理性，通过自制的悬浮速度测量装置对一定几何尺寸的甘蔗叶的最小悬浮速度进行了试验验证。

3.1 试验装置与测量仪器

自制的试验测量装置见图2所示。其中，D为调节风机转速的变频器，其调节范围为0～50Hz；风速仪为testo405-V1手持式测速仪，其测量范围为0～20m/s，精度为0.01m/s；称重计最大量程为10kg，精度为0.1g；蔗叶的几何尺寸采用游标卡尺测量。

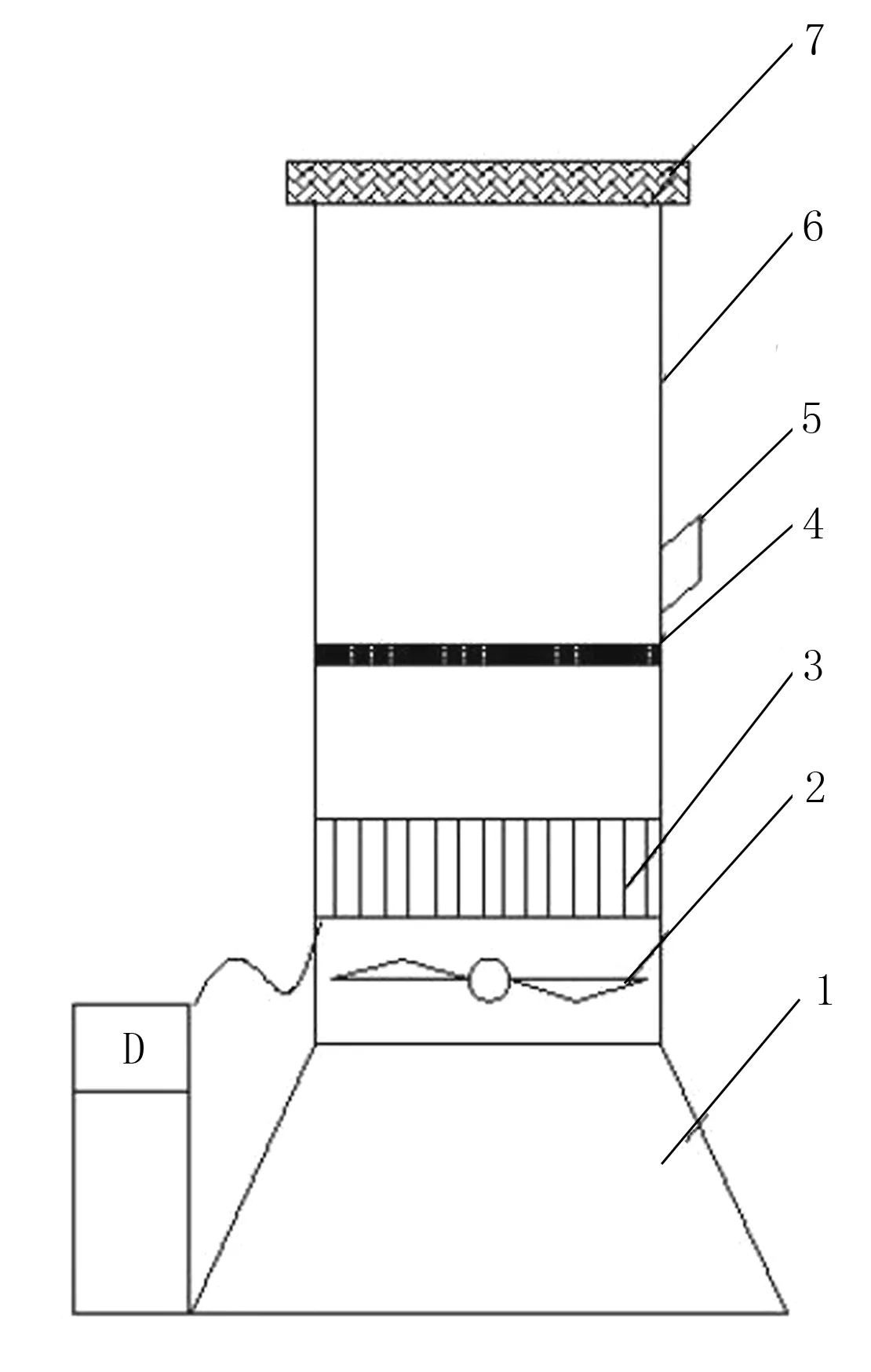
图2 悬浮速度测量装置

3.2 试验材料

试验样品为成熟甘蔗上采取的甘蔗青叶中间段，取自学校某试验基地，其含水率处于71.01%～73.14%，平均宽度处于3.1～4.2cm之间。表1为试验样品的其他基本参数。

表1 试验样品参数

3.3 测试装置精度验证

由于是自制悬浮速度装置，先需要验证测试装置是否满足悬浮速度的测试要求。验证采用的方法为：对物料网上方的玻璃圆管径向截取5个等距截面，每个截面按等面积同心圆环原理选取7个测点，设测点从左至右为测点1～测点7。当变频器示数为45Hz时，各个截面上风速的测量结果如表2所示。

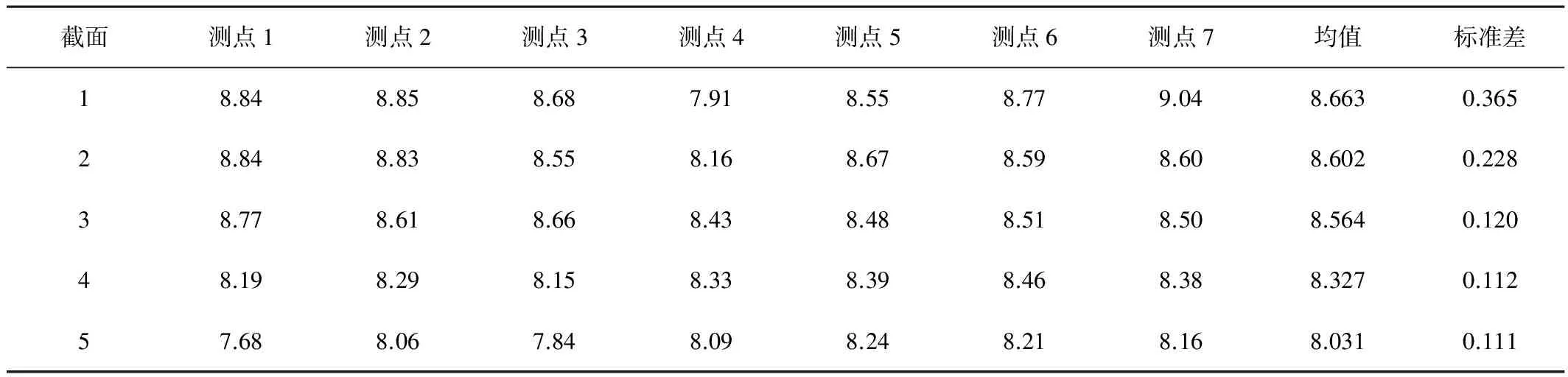
表2 截面上风速测量结果(变频器读数为45Hz)

从表2中测量数据可知:试验装置可满足悬浮速度试验的测量要求。

3.4 测量方法

首先将样品置于物料网中央，调节变频器，使蔗叶段在气流作用下上升进入测量段并保持其悬浮，通过玻璃圆管边上的标尺记下此时蔗叶上升的高度和变频器的读数；取出样品后，再将变频器调至相同的读数，测量标记位置所处截面风速即为最小悬浮速度。每一样品在同一条件下测量3次，取3次平均值作为蔗叶的最小悬浮速度。

3.5 测量结果

将测量所得结果与传统悬浮速度计算方法和本文提供的计算方法所得结果相比较，如图3所示。

图3 3种方式所得结果比较图

4 结论

通过分析片状体在垂直流场中的受力，建立了一种相对简单的悬浮速度计算模型。该模型相比传统悬浮速度计算方法更加简洁，计算结果更接近试验测量结果。试验验证发现：在计算片状体最小悬浮速度时，本文提供的计算模型相比传统方法关于不规则颗粒悬浮速度的计算方法具有明显的优越性；但对尺寸较小的片状体，其计算结果也存在较大误差。

[1] 干方建，潘晓阳，胡开文. 烟草物料风力输送速度的分析和研究[J].合肥工业大学学报，1999 ，22(2)：131-133.

[2] 彭建恩. 物料悬浮速度的研究[J].粮食科技与经济，2001(4)：37.

[3] 张佳，庄卫东，陈彬. 农业物料悬浮速度试验台的研制[J]. 黑龙江八一农垦大学学报，1998，10(3)：56-59.

[4] 李学军，陈嘉真. 茶叶在空气流中的悬浮速度[J].茶叶科学，1987，7(1)：63-64.

[5] 谭子成. 关于颗粒悬浮速度概念的引申[J].通风除尘，1992(2)：20-21.

[6] 李爱平，汪春. 苜蓿段长度对干燥速度与悬浮速度影响的试验[J]. 农业机械学报,2006 (8):169-171.

[7] 周作伸，刘贵富. 羽毛空气动力学特性的试验研究[J]. 农业机械学报,1989(1):48-52.

[8] 张继成,陈海涛,纪文艺,等.大豆脱出物悬浮速度试验研究[J].农机化研究，2013,35(4)：127-131.

[9] 王维，王娅妮.物料悬浮速度测试台的设计与试验研究[J].中国农机化学报，2016(6)：45-46.

[10] 须山启介，清水浩.单一谷粒悬浮速度研究[J].粮食与饲料工业, 1984(2):265-269.

A Calculation Model for the Minimum Suspension Velocity of a Sheet

Yuan Chengyu, Wang Juan, Chen Zhishui, Liao Yulan

(college of mechanical and electrical engineering, Hainan University,Haikou 570228, China)

The minimum suspension velocity of the sheet bodies can be obtained by conventional theoretical calculations and experimental. In the paper, the author provided a computing model of sheet bodies’ minimum suspension velocity in the pressure drag area. and conducted a verification test in sugarcane leaves through the self-made test device. The result showed that the sugarcane leaves minimal suspension speed by traditional theoretical calculations is large difference with the results of experimental measurements, the maximum relative error was 97.3% and the minimum relative error is 39.4%; while the calculation result by this paper is small difference with the results of experimental measurements,the maximum relative error is 24.9% and the minimum relative error is 4.75%.

sheet body; minimum suspension velocity; mathematical model

2016-07-07

海南省自然科学基金项目(20163061)

袁成宇(1976-),男，湖南邵阳人，副教授，在职博士研究生，(E-mail)ycy@hainu.edu.cn。

S183

A

1003-188X(2017)08-0062-04