发展动量分辨的含时密度泛函理论，实时模拟石墨烯纳米带的激发态

胡史奇，廉超，关梦雪，孟胜,2*

1.中国科学院物理研究所北京凝聚态物理国家实验室，北京 100190

2.量子物质科学协同创新中心，北京 100190

发展动量分辨的含时密度泛函理论，实时模拟石墨烯纳米带的激发态

胡史奇1，廉超1，关梦雪1，孟胜1,2*

1.中国科学院物理研究所北京凝聚态物理国家实验室，北京 100190

2.量子物质科学协同创新中心，北京 100190

实时的密度泛函理论 (real-time Time Dependent Density Functional Theory，或称 rt-TDDFT) 是基于含时 Kohn-Sham 方程，从实空间实时模拟体系激发态性质的第一性原理计算方法。本文介绍如何利用自主开发的动量分辨的含时密度泛函理论计算方法和软件 Time Dependent ab initio Package (TDAP)，研究具有较大尺寸的石墨烯纳米体系的激发态性质。以石墨烯扶手椅型纳米带 (Armchair graphenenanoribbons，AGNRs) 为例，通过直接模拟外加光场下多电子体系的波函数实时演化，得到了体系的光吸收谱以及激发态的动力学过程。这样的计算方法大大提高了周期性体系的计算效率，且不再受微扰论的限制，实现了对大规模、真实体系的动力学性质的实时模拟。

第一性原理计算；含时密度泛函；激发态模拟；石墨烯

引言

上世纪七十年代以来，伴随着计算机技术的飞速发展，密度泛函理论[1](Density Functional Theory，DFT) 在固体物理学计算中的成功使得第一性原理计算在模拟原子尺度物理化学过程、理解预测材料的机理和性质、发现设计新型功能材料等领域得到了广泛的应用。作为一种研究多电子体系电子结构的量子力学方法，密度泛函理论利用电子体系基态总能量是电子密度的唯一泛函的假设，将复杂的电子相互作用融入到交换关联能量项中，通过对其取局域密度或更高级的近似，得到了类似单粒子薛定谔方程形式的Kohn-Sham 方程。实际计算中，为方便求解，一般通过傅里叶变换的办法将 Kohn-Sham 方程从实空间求解转化到共轭动量所在的空间求解。结合自洽计算方法，通过变分求 Kohn-Sham 方程决定的总能量极小值点，得到体系在基态时的能量及性质。密度泛函理论在凝聚态体系基态性质中的计算取得了令人满意的结果，是凝聚态物理、计算材料学和计算化学领域最常用的方法之一。

但是通常的密度泛函理论仅对于多电子体系的基态成立，对于电子激发态，原则上不存在电子密度和体系真正的多体波函数的一一对应关系，因此无法用普通的 Kohn-Sham 方程描述。然而，E.Runge 和E.K.U.Gross 于 1984年发现[2]，如果初态多体波函数给定，那么随时间变化的电子密度和随时间变化的体系多体波函数也具有严格的一一对应关系，此即含时密度泛函理论。依据含时密度泛函理论，体系的激发态性质原则上可以严格求解，在实际应用中则需要对时间相关的交换关联泛函取近似，并发展实际可行的算法。

一种实际办法就是实时求解含时密度泛函方程(real-time Time Dependent Density Functional Theory，或称 rt-TDDFT)，直接模拟体系的激发态性质。相比于传统的基于准粒子修正描述激发态行为的格林函数方法，rt-TDDFT 包含了所有的非线性效应，摆脱了微扰论要求的必须在平衡态附近应用的限制。同时，rt-TDDFT 方法提供了电子波函数实时的演化过程，结合离子动力学，能够直观地给出离子-电子多体体系随时间的演化路径。因此，rt-TDDFT 成为计算模拟强场物理、超快物理过程的有效工具。

然而，受限于计算效率，传统的 rt-TDDFT 大多只能在动量空间的单点上进行计算，无法实现体系的动量分辨。这一限制意味着传统的 rt-TDDFT 无法对周期性的体系进行有效大规模模拟，只能限于原子团簇等零维非周期体系。同时，传统的 rt-TDDFT 大都只考虑了电子的演化进程，而不涉及离子动力学对电子状态的影响。这些都大大限制了 rt-TDDFT 理论的应用范围，从而阻碍了 rt-TDDFT 在物理、材料计算领域的应用和发展。基于上述现状，我们发展了一套具有动量空间分辨能力，并且考虑离子动力学过程的 rt-TDDFT 计算方法和软件 TDAP (Time Dependent ab initio Package)[3-4]。基于 TDAP，我们不仅实现了周期性体系的激发态性质的计算模拟，同时计算效率也大大提高。我们选取了近年来的热点体系—扶手椅型石墨烯纳米带 (Armchair graphenenanoribbons 或称AGNRs) 作为研究对象，通过外加光场的方式，模拟了不同尺寸 AGNRs 的光吸收行为以及不同吸收模式下的激发态动力学过程。我们发展的模拟方法实现了电子激发模式在动量空间的分辨，摆脱了传统微扰论的限制，同时也提高了计算效率。

1 原理方法

1.1 含时 Kohn-Sham 方程

多电子体系的哈密顿量为:

其中第一、二项代表了电子与离子的运动动能，第三项、第四项分别代表了电子间、离子间的库伦相互作用，第五项代表了电子-离子之间的相互作用，最后一项则描述了外势场。此时电子体系的量子行为一般采用薛定谔方程进行描述，在 rt-TDDFT 理论中，多体电子体系的薛定谔方程可以在一定程度上简化为单粒子形式的含时 Kohn-Sham (Time-dependent Kohn-Sham，TDKS) 方程[3]：

其中，φj(r,t) 为第j个电子的单粒子波函数，第二项描述了外场的贡献，第三项表示了电子的库伦相互势能项，第四项描述了离子提供的势场，而电子-电子之间的交换关联作用，被写入最后一项交换关联能中。

1.2 电子波函数演化求解

对于体系激发态性质的描述可以通过求解 TDKS方程得到，各时刻的电子密度矩阵由单粒子波函数表示。同时，t+dt时刻单电子波函数可以通过t时刻的波函数演化得到[4]：

其中Sk(t') 为动量k标记的波函数的交叠矩阵，Hk(t')为动量k标记的t' 时刻的哈密顿量，二者又依赖于此时的电子密度。因此，可以用自洽计算描述电子体系的演化。演化过程中，电子各时刻的不同k点能级变化可以通过对该时刻哈密顿量进行对角化求解本征值得到[4]：

同时，跃迁占据数也由演化的 TDKS 波函数和各时刻哈密度量对角化的本征态基矢的内积表示：

2 离子动力学过程

根据 Ehrenfest 理论，在忽略离子间的交换关联相互作用后，离子的运动状态可以利用经典的牛顿方程来描述[3]：

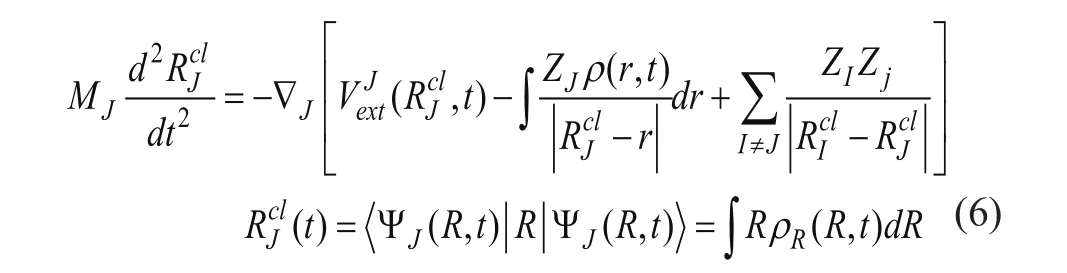
3 原子轨道基矢

图1 TDAP 计算框架Fig.1 Flowchart of TDAP algorithm

TDAP 是基于 Siesta 计算软件。在计算中，我们采用数值原子轨道基矢 (Numerical Atomic orbital 或称 NAOs) 作为展开。相比于平面波基矢，原子轨道基矢由于其局域特性大大提高了收敛速度。因此，原子轨道基矢的使用在保证精度的同时提高了计算的速度。对于有Nn个 TDKS 轨道，No个原子轨道基矢的体系，计算速率呈现NnO(No2) 的依赖关系，对激发态的模拟时长也得到提高。

4 激发态模拟

计算中，对体系的激励来自于模拟的外界光场，这样的外加光场在程序上的实现是通过对哈密顿量中的外势进行改造，添加外界光场产生的势。这里，主要考虑光的电场分量[4]：

对于周期性体系而言，周期性电荷密度分布的限制导致电场的施加必须以存在真空层为前提，因此计算中，电场方向应该沿体系的非周期性方向。实际模拟中，主要采用两种外加电场形式，对材料吸收特性的模拟，采用包含各个频率分量的阶跃场E(t)=E(1-Θ(t))；对激发态电子动力学过程的考察采用特定频率的正弦场：E(t)=Esin (2πft+φ)。根据电偶极矩与外加电场的关系：P(ω)=ε(ω)E(ω)，施加电场激励后，通过探测体系不同时刻电偶极矩的响应可以得到体系的介电性质：

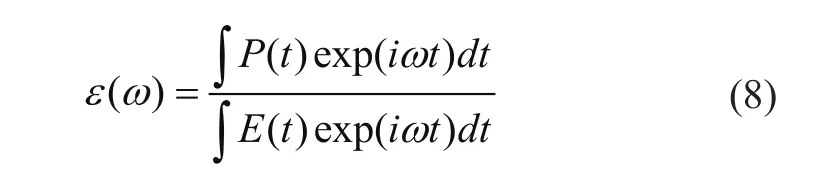
进而可以得到体系吸收谱性质：Abs(ω)∝ Im(ε(ω))，以及能量损失谱 (EELS) 性质：EELS(ω)∝-Im(1/ε(ω))。

5 结果与讨论

图2 石墨烯纳米带光场激发示意图Fig.2 The schematic showing the GNRs under an electric field

首先计算石墨烯纳米带的基态电子结构。我们采用 Siesta 软件包，采用模守恒赝势和局域密度近似，在数值原子轨道基的基础上对石墨烯纳米带的结构进行了弛豫。其中k点的选取为 1×1×24，能量收敛精度为 10-4eV。在此基础上，我们利用 TDAP，通过模拟沿宽度方向的外界光场，计算了石墨烯纳米带的吸收谱、能量损失谱等性质。在对吸收谱与能量损失谱的模拟中，我们采用阶跃电场，场强大小为0.25V/Å，模拟时间为 24fs，同时选取 1×1×32 的动量空间分布。随后，我们将 TDAP 的模拟结果与 DFT、TDDFT 线性响应的结果进行了对比，测试了程序的可靠性。在得到吸收性质的基础上，对激发态电子的动力学过程进行了探讨。得到了不同吸收模式下的激发动力学。对于激发动力学的模拟，我们采用正弦电场，场强大小为 0.125V/Å，模拟时间为 50fs，选取1×1×32 的动量空间分布。

5.1 石墨烯纳米带的光吸收谱与能量损失谱

图3给出了不同宽度不同能量区域石墨烯纳米带的吸收谱特性，根据不同能量区域，光吸收存在两个模式：可见光区域的模式和高能量区域的模式。两类模式的共振吸收能量均随着宽度的增加而红移。其中，高能量区域的吸收模式为主导，其共振吸收能量大约在 5-7eV。对比石墨烯纳米带的计算结果与DFT、DFT+GW 计算得到的石墨烯吸收谱[6,7]，可以发现，随着宽度增加，两类吸收模式以不同的方式趋向于无限大尺寸的二维石墨烯材料的行为。其中，对可见光区域，随宽度增加，各吸收峰逐渐展宽最终形成趋向于石墨烯 2.3% 的吸收平台区。对于高能量区域模式，随着宽度的增加，其吸收峰能量逐渐趋向于石墨烯的π能带跃迁。相较于基态的 DFT 计算，TDAP 的计算更趋向于包含准粒子修正的 DFT+GW的计算结果，从侧面也印证了 TDAP 对激发态特性描述的合理性。

图4中对比了对应不同波矢的各宽度石墨烯纳米带电子能量损失谱的 TDAP 计算结果与利用频率空间 TDDFT 线性响应理论得到的石墨烯电子能量损失谱[5]。可以看出，不同宽度的石墨烯纳米带中的激发态，在一定意义上可以看做是石墨烯对应不同波失的激发模式。二者在不同能量区域的分布均呈现出一致性。其中 5-7eV 的区域对应于石墨烯的π能带带间等离激元。二者分布趋势的一致性不仅是石墨烯纳米带与无限大石墨烯片的电子结构密切关联的体现，也说明了 TDAP 程序在激发态计算中的准确性。同时，体系的区别导致二维石墨烯内部电子与石墨烯纳米带带间库伦相互作用存在差异，也使得二者在能量损失谱中细节上的不同。比如可见光区域，石墨烯纳米带的能量损失谱呈现一个峰值分布的振荡，而石墨烯的能量损失谱呈现均一的的平台。

图3 不同宽度石墨烯纳米带与石墨烯的吸收谱，其中 N 为整个石墨烯纳米带沿宽度方向碳原子二聚体的数目Fig.3 Absorption spectrum of grapheme and AGNRs with different widths,N is the number of dimer lines along the ribbon width.

图4 (a) 石墨烯与 (b) 石墨烯纳米带的电子能量损失谱Fig.4 Electron Energy Loss Spectroscopy (EELS) of (a)grapheme and (b) AGNRs.

5.2 石墨烯纳米带激发态电子动力学

吸收谱和电子能量损失谱对TDAP与DFT+GW以及TDDFT线性响应理论计算的比较验证了自主发展的程序在计算激发态时结果的合理性。在此基础上，有别于基态的计算，借助TDAP计算效率的优势，我们进一步考察了石墨烯纳米带体系不同吸收模式下的激发态电子动力学过程。动力学过程能够更为直观的给出激发态电子波函数随时间变化的行为。

图5 碳原子二聚体数目为 6 的石墨烯纳米带 (a) 可见光吸收模式与 (b) 高能吸收模式激发电子总量 (蓝点)，体系总能量 (红点) 与电偶极矩 (绿线) 随时间变化，其中黑线为外加电场随时间的变化。Fig.5 The total excited electrons (blue),total energy (red) and dipole (green) for (a) visible light mode and (b) high energy mode on6-AGNRs,black line shows the electric field.

图5 给出碳原子二聚体数目N为6的石墨烯纳米带(6-AGNR) 可见光区域与高能量区域不同吸收模式对应的激发量，总能量以及电偶极矩随时间的变化。其中黑线描述了外界光场的振荡。可以看出，对于不同的吸收模式，电子激发量、总能量以及电偶极矩随时间变化有所差别，意味着不同的激发态电子行为。

图6 不同时刻下，碳原子二聚体数目为6的石墨烯纳米带的(a)可见光吸收模式与 (b) 高能吸收模式的电子激发量在不同k点上的分布。其中红色表示占据数增加，蓝色表示占据数减少，圆圈大小代表了变化数的多少。Fig.6 Theexcited electrons with k resolution at different times for (a) visible light mode and (b) high energy mode on 6-AGNRs.Red (blue) represents the increase (decrease) of electrons andcircle size is proportional to the population.

借助 TDAP 对不同动量的分辨能力，图6展示了碳原子二聚体数目为6的石墨烯纳米带不同吸收模式激发过程中，能带上不同k点电子占据数随时间的变化，对比两类的吸收模式，电子的激发跃迁在k空间分布存在差别。对于可见光模式，电子的激发趋向于个体k点，相比之下，高能吸收模式中，电子的激发分布于多个k点，趋向于集体性质的k点分布。因此，可见光吸收模式有着个体激发的特征，而高能模式包含更多集体激发的特点。

6 结论

本文从计算原理与算法的角度，首先介绍了含时密度泛函理论在计算体系激发态性质方面的应用。作为基于 TDKS 演化方程的计算理论，rt-TDDFT 包含了所有的非线性效应，提供了电子波函数随时间变化的行为，能够直观地给出体系随时间的演化路径。同时，受限于计算效率，传统的 rt-TDDFT 大都无法实现体系的动量分辨，并且无法考虑离子运动对电子态变化的影响。这样的限制意味着其只能限于原子团簇等零维非周期体系的电子演化计算。基于此，我们发展了包含动量分辨，同时考虑离子动力学过程的 rt-TDDFT 计算程序 TDAP。我们利用 TDAP 计算了石墨烯纳米带的吸收特性，以及不同吸收模式下的电子动力学过程。通过与已有体的计算结果进行对比，计算结果不仅验证了程序的可靠性与高效性，同时也给出了石墨烯纳米带体系激发态的动力学图像。本文能够对激发态的计算模拟、以及材料激发特性的理解与应用提供参考价值。

[1]P.Hohenberg and W.Kohn,Phys.Rev.136,B864 (1964).

[2]E.Runge and E.K.U.Gross,Phys.Rev.Lett.52,997(1984).

[3]S.Meng and E.Kaxiras,J.Chem.Phys.129,054110(2008).

[4]C.Lian,S.-Q.Hu,M.-X.Guan,and S.Meng,arXiv:1702.08163v1(2017).

[5]C.Vacacela Gomez,M.Pisarra,M.Gravina,J.M.Pitarke,and A.Sindona,Phys.Rev.Lett.117,116801(2016).

[6]O.V Sedelnikova,L.G.Bulusheva,and a V Okotrub,J.Chem.Phys.134,244707 (2011).

[7]P.E.Trevisanutto,M.Holzmann,M.Côté,and V.Olevano,Phys.Rev.B.81,121405(2010).

Momentum-Resolved rt-TDDFT Algorithm for Modeling Electronic Excitation in Graphene Nanoribbons

Hu Shiqi1,Lian Chao1,Guan Mengxue1,Meng Sheng1,2*

1.Beijing National Laboratory for Condensed Matter Physics,Insitute of Physics,Chinese Academy of Sciences,Beijing 10018,China
2.Collaborative Innovation Center of Quantum Material,Beijing 100871,China

Real-time (rt) time dependent density functional theory (TDDFT) is an efficient ab initio method to study electronic dynamics in real time and real electron-nuclear space.The method is based on time dependent evolution of Kohn-Sham (TDKS) orbitals.Here we report first-principles simulations on electronic excitation dynamics in grapheme nanoribbons (AGNRs) using our home-built Time Dependent ab initio Package (TDAP).We obtain optical absorption spectrum and electron energy loss spectrum (EELS) via applying an external field to AGNRs and then analyze the dynamic evolution of electronic excited states.This algorithm represents an effective way to simulate electronic excitations in periodic systems beyond the limit of perturbation theory.

ab initio method; TDDFT; electronic excitation; graphene

10.11871/j.issn.1674-9480.2017.02.007

国家重点研发计划 (2016YFA0300902、2015CB921001)；国家自然科学基金 (11774396)

*通讯作者：孟胜(smeng@iphy.ac.cn)

2017年1月13日

胡史奇：中国科学院物理研究所，博士，主要研究方向为低维材料的激发态电子性质模拟。

E-mail:isqhu@iphy.ac.cn

廉 超：中国科学院物理研究所，博士，主要研究方向为激发态的电子动力学行为模拟。

E-mail:chaolian@iphy.ac.cn

关梦雪：中国科学院物理研究所，博士，主要研究方向为低维材料的激发态电子性质模拟。

E-mail:mxguan@iphy.ac.cn

孟 胜：中国科学院物理研究所，量子物质科学协同创新中心，研究员，博士生导师，主要研究方向为激发态的电子动力学行为，新能源器件物理以及表面水结构研究。

E-mail:smeng@iphy.ac.cn