LDPC码性能研究与分析

张连连 郭 伟 吉高卿 戴泽华

(1.河北建筑工程学院电气工程学院，河北 张家口 075000;2.张家口市交通运输局，河北 张家口 075000)

LDPC码性能研究与分析

张连连1郭 伟1吉高卿1戴泽华2

(1.河北建筑工程学院电气工程学院，河北 张家口 075000;2.张家口市交通运输局，河北 张家口 075000)

1/2码率的二元LDPC码在AWGN信道下是距Shannon极限最近的纠错码.在matlab中采用随机构造法构造校验矩阵及软判决译码对LDPC进行了设计实现，并分析了三种不同形式的校验矩阵对LDPC码性能的影响，得出近似下三角形式校验矩阵的编码方法优于其他两种.

LDPC；误码率；软判决译码；校验矩阵

0 前 言

低密度奇偶校验码(Low Density Parity Check Code，LDPC码)[1]于1962年由Gallagar提出，经过Mackey、Spielman和Wiberg[2]等人的研究发现LDPC码具有全并行迭代译码结构、便于硬件实现、性能优越等优点，因此LDPC在深空通信、光纤通信、卫星数字视频和音频广播等领域等得到了广泛应用[3].本文研究了LDPC的随机构造法构造校验矩阵及软判决译码，分析了校验矩阵的多种变换方法，对不同校验矩阵对LDPC的性能影响进行了研究.

1 LDPC的编码算法

二元LDPC码是一种低密度线性分组码，其校验矩阵H具有稀疏性的特点，即H中大部分为“0”，数量很少的元素为“1”.正则LDPC码的定义由Gallager给出，H应满足以下条件：每一行有ρ个“1”，ρ为该行的行重；每一列有γ个“1”，γ为该列的列重；任意两行或者两列不会有两处或两处以上在相同的位置有“1”；ρ和γ远远小于码长.LDPC的编码步骤概括如下：

(1)低密度校验矩阵构造的LDPC码由校验矩阵确定，编码时需先构造一个校验矩阵.假设已经构造了一个校验矩阵H,从码字空间中选出一组可用码字作为所需构造的LDPC码.

(2)通过高斯消元将校验矩阵H转化为形式：H=[,I]，I为单位矩阵，方便在译码时确定信息比特位置.

(3)利用校验矩阵得到生成矩阵G=[I,P].

(4)得到编码输出码字C=xG=[x,xp]，即信息序列x乘以生成矩阵G.

校验矩阵H是LDPC的重要特性，H不同则码字集合也不同，因此校验矩阵对LDPC码的构造尤为重要.H构造时先生成一个的全0矩阵，然后随机地将每列中的γ个0置换成1，每行当中的ρ个0置换成1.为保证LDPC码的正确性同时需避免以下两种情况：一是避免出现长度为4的环，否则可能导致消息在两组点之间的反复传递.二是避免比特节点所连接的校验方程过于集中，否则会导致LDPC码错误.

2 LDPC的译码算法

置信传播算法(Belief Propagation Algorithm)是LDPC软判决译码的一种迭代概率译码算法，各个节点之间传递的信息是概率或置信信息.每一轮迭代都需要对码字中各个比特关于接收码字和信道参数的后验概率进行估算，因此BP译码算法是一种逐比特最大后验概率算法，具体步骤分为初始化、迭代过程和译码判决三部分[4].

2.1 初始化

通过公式(2-1)计算信道传递给变量节点的初始概率，对每一个节点和与其相邻的校验节点j∈C(i)，变量节点传向校验节点的初始消息通过公式(2-2)、(2-3)设定.

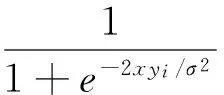
(2-1)

(2-2)

(2-3)

2.2 迭代过程

通过迭代步骤，对每一比特的后验概率进行精确的估算.

1、水平过程

对所有的校验节点j和与其相邻的变量节点j∈R(j)，第l次迭代时，通过公式(2-4)、(2-5)计算变量节点传向校验节点的消息，其中l为迭代次数.

(2-4)

(2-5)

2、垂直过程

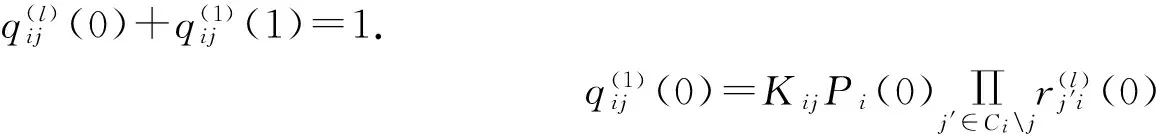
(2-6)

(2-7)

2.3 译码判决

通过公式(2-8)、(2-9)对所有变量节点计算硬判决消息，其中Ki是校正因子，使得Qi(0)+Qi(1)=1.

(2-8)

(2-9)

若Qi(1)>Qi(0)，则ci=1，否则ci=0，得出对发送码字的一个估计c=[c1,c2,…，cn].计算伴随式S=cHT，如果S=0，则译码成功，结束迭代过程；否则跳转到迭代过程继续进行迭代译码.若迭代次数达到预先设定的最大次数仍未成功，则宣告失败，终止迭代.

3 H矩阵变换方法对性能的影响

在matlab对LDPC的编译码过程进行了设计实现，采用了传统的高斯消元法、基于下三角形式校验矩阵以及基于近似下三角形式校验矩阵的编码方法对LDPC码误码率进行分析和比较.对列重为4的校验矩阵H进行变换，将其分别变换为G=[I P]、下三角、近似下三角形式，如图3-1(a)、(b)、(c)所示.

图3.2 三种编码方式LDPC码的误码性能对比

由图3-1(a)、(b)、(c)可以明显看出，高斯消元转换为G=[I P]的过程破坏了H的稀疏性，P中可能出现较多的短环而影响LDPC码的性能；转换成下三角形式以及近似下三角形式的H矩阵仍具有稀疏性的特点，其仿真编码时间比传统编码要少.

通过分析仿真时长发现，列重较小时三种编码方式除编码时间的差别外其LDPC码的误码率差别并不大；随着列重的增大，H矩阵并不一定能够通过高斯消元转换成G=[I P]的形式，所以基于下三角形式以及近似下三角形势H矩阵的LDPC码误码性能渐渐优于传统编码方.观察图3.2可以看出基于下三角形式编码方法以及基于近似下三角形式编码方法在同一信噪比的情况下，二者均优于G=[I P]的编码方法，且随着信噪比的提高优势愈加明显.近似下三角形式校验矩阵的编码方法要优于下三角矩阵但是这种优势并不是特别明显.

[1]R.G.Gallager.Low-Density Parity-Check Codes[J].IRE Transaction On Information Theory,1962

[2]R.M.Tanner.A Recursive Approach to Low Complexity Codes[J].IEEE Transactions on Information.Theory,Sept.1981,V27:533～547

[3]王鹏.LDPC码的编译码原理及编码设计[D].西安电子科技大学,2004年1月

[4]唐启荣.LDPC编码的研究与硬件实现[D].北京邮电大学,2007年3月

[5]Xiali Yan,Wenquan Feng,Qi Zhao and Hongbo Zhao.Modified Log-BP decoding algorithm combined with PSO for Low-Density Parity Check Codes.2010 3rdInternational Conference on Advanced Computer Theory and Engineering(ICACTE2010), V2:443～447

ResearchandAnalysisonthePerformanceofLDPCCodes

ZHANGLian-lian1，GUOWei1，JIGao-qing1，DAIZe-hua2

(1.Hebei Institute of Architecture and Civil Engineering,Hebei Zhangjiakou 075000；2.Xhhangjiakou Transportation Bueau,Hebei Zhangjiakou 075000)

The performance of half of the binary bit-rate LDPC codes in AWGN channel is the latest error-correcting codes to the Shannon Limit.In MATLAB,the LDPC was designed and implemented by using the random construction method to construct the verification matrix and soft decision decoding,and the effect of three different forms of check matrix is analyzed on the performance of LDPC codes.it is concluded that the approximate lower triangular form of check matrix coding method is better than the other two.

LDPC;bit error rate;soft decision decoding;parity check matrix

2017-03-29

2014河北建筑工程学院科研基金项目，项目名称：三网融合技术在建筑电视网中的应用，项目编号：Y201415

张连连(1984-)，女，讲师，从事信息与通信工程研究.

10.3969/j.issn.1008-4185.2017.03.015

TN911.22

A