考虑时空离散性的高压直流输电系统换相失败评估方法*
2017-12-15蔡泽祥杨欢欢余超耘李晓华
蔡泽祥 杨欢欢 余超耘 李晓华
(华南理工大学 电力学院, 广东 广州 510640)
考虑时空离散性的高压直流输电系统换相失败评估方法*
蔡泽祥 杨欢欢 余超耘 李晓华
(华南理工大学 电力学院, 广东 广州 510640)
直流输电系统换相失败的特性随交流故障合闸角和故障位置的不同而不同,目前只考虑换流母线电压幅值跌落的直流系统换相失败判别方法准确性不高.文中研究了换相失败的时空离散性,分析了故障合闸角对换相失败的影响过程,指出最不利于换相的故障时刻,并且揭示了故障位置对换相失败的影响主要源于故障点与直流逆变母线之间电气距离和相位的差异.基于对换相失败时空离散性的分析,提出了同时计及电压幅值与相位变化的熄弧角判据和以此为基础的换相失败评估方法.以南方电网三节点AC/DC系统为背景,通过与PSCAD/EMTDC、BPA仿真结果的对比验证了该评估方法的有效性和实用性.
高压直流输电;换相;时空离散性;电压幅值;相位变化;熄弧角;评估方法
近年来,我国电网发生了多起交流故障引发直流换相失败、甚至多回直流同时换相失败的事故[1- 6],严重情况下甚至导致直流闭锁.直流闭锁造成的功率扰动可能给受端交流系统带来稳定性问题[7],构成电网安全稳定运行的新约束.因此,有必要对换相失败的机理和评估建立系统的认识[8- 10].
换相失败的准确判别是换相失败评估的基础.目前,换相失败的判别方法主要有两种.一种是基于PSCAD/EMTDC等电磁暂态仿真软件对换相过程进行详细建模,通过监测阀电流来判别直流是否换相失败;该方法较为精确,但耗时长,特别对于大规模的系统,效率极低.另一种是在BPA等机电暂态仿真软件中通过换流母线电压幅值或熄弧角进行判别[11- 16].工程上就常以故障后换流母线电压幅值跌至稳态值的80%作为换相失败的判据.至于熄弧角判据,由于其计算方程只考虑了电压幅值的跌落,因而与电压判据本质上是一致的.
根据大量的现场故障录波和仿真实验,造成同一直流换相失败的交流故障无论在时间、空间或类型上都具有离散性,而且在不同故障条件下,直流发生换相失败的临界换流母线电压幅值水平存在差异[17- 19].这说明,只考虑电压幅值因素的换相失败判据不够准确.出现上述情况的原因是,交流故障的时空条件差异导致换流母线电压幅值与相位的变化情况均不相同,而电压的幅值与相位共同影响着熄弧角的大小.因此,换相失败的判别需要同时计及电压幅值与相位变化两个因素.
本研究针对换相失败的时空离散性展开研究,分析了不同故障合闸角和故障位置导致直流换相失败特性存在差异的机理,揭示了换相失败时空离散性的产生机理;在此基础上,提出一种适用于交直流互联大电网的换相失败评估的方法,以期为电网的规划运行提供指导.
1 换相失败时空离散性分析
1.1 换相失败的时间离散性
换相失败的时间离散性指在不同时刻发生同一交流故障时,直流是否发生换相失败存在差异.
当直流电流在定电流控制与平波电抗器的作用下保持恒定时,换相成功所需的最小换相电压时间面积S0是确定的[20- 21]:
S0=2LrId
(1)
式中,Lr为每相等值换相电感,Id为直流电流.
最大换相电压时间面积S取决于最大换相角μmax和换相电压曲线.根据式(2)可知μmax与换相成功需要保证的最小熄弧角γmin相对应.
γmin=β-μmax
(2)
式中,β为换流阀的超前触发角.
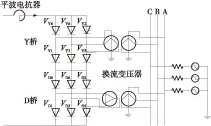
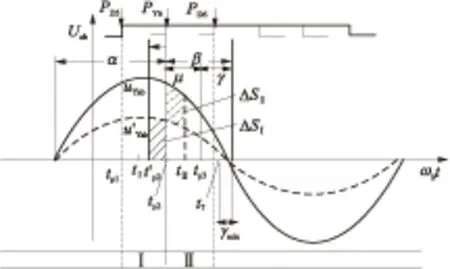
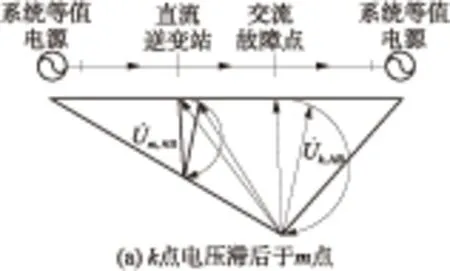
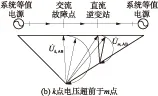
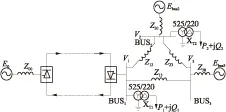
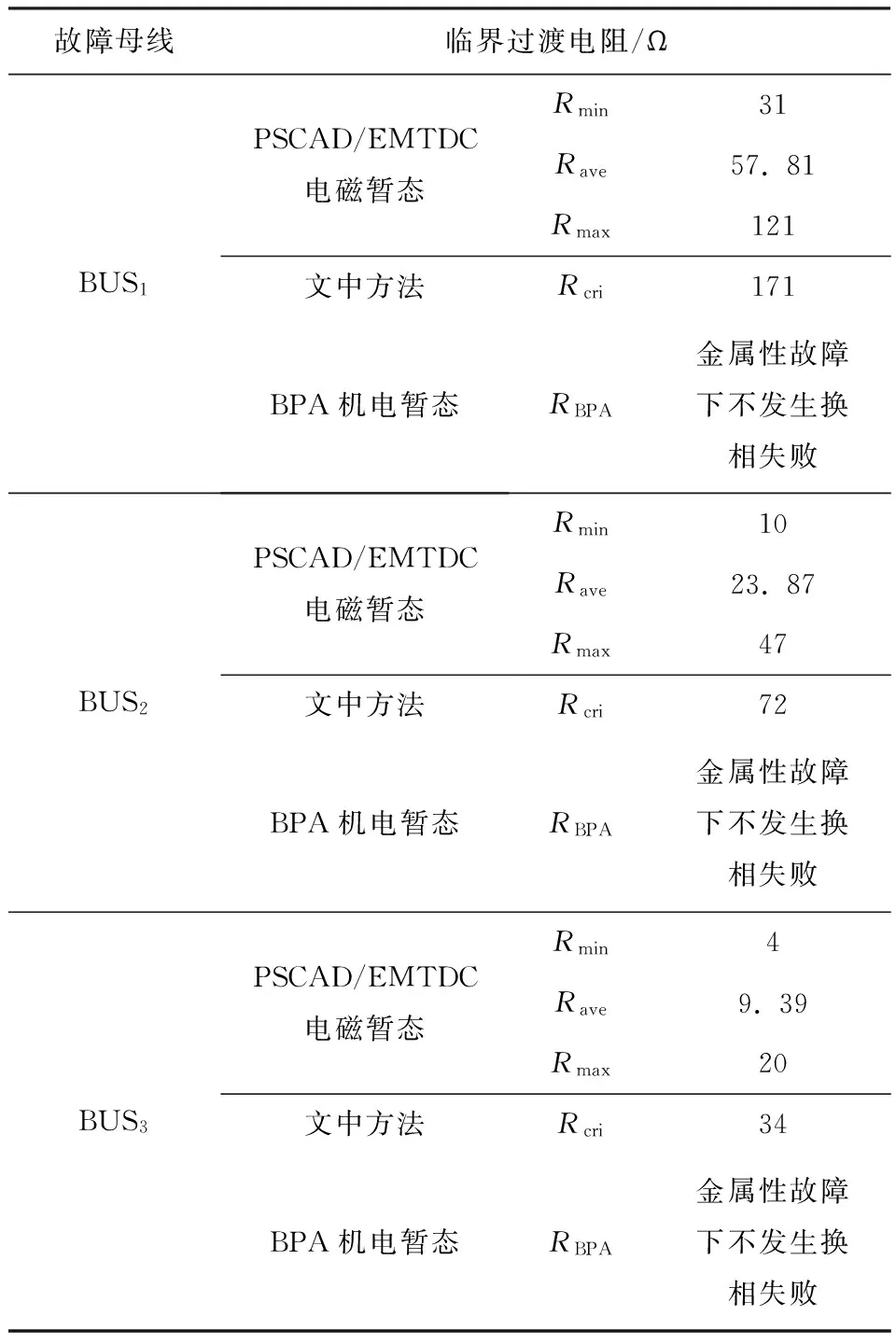
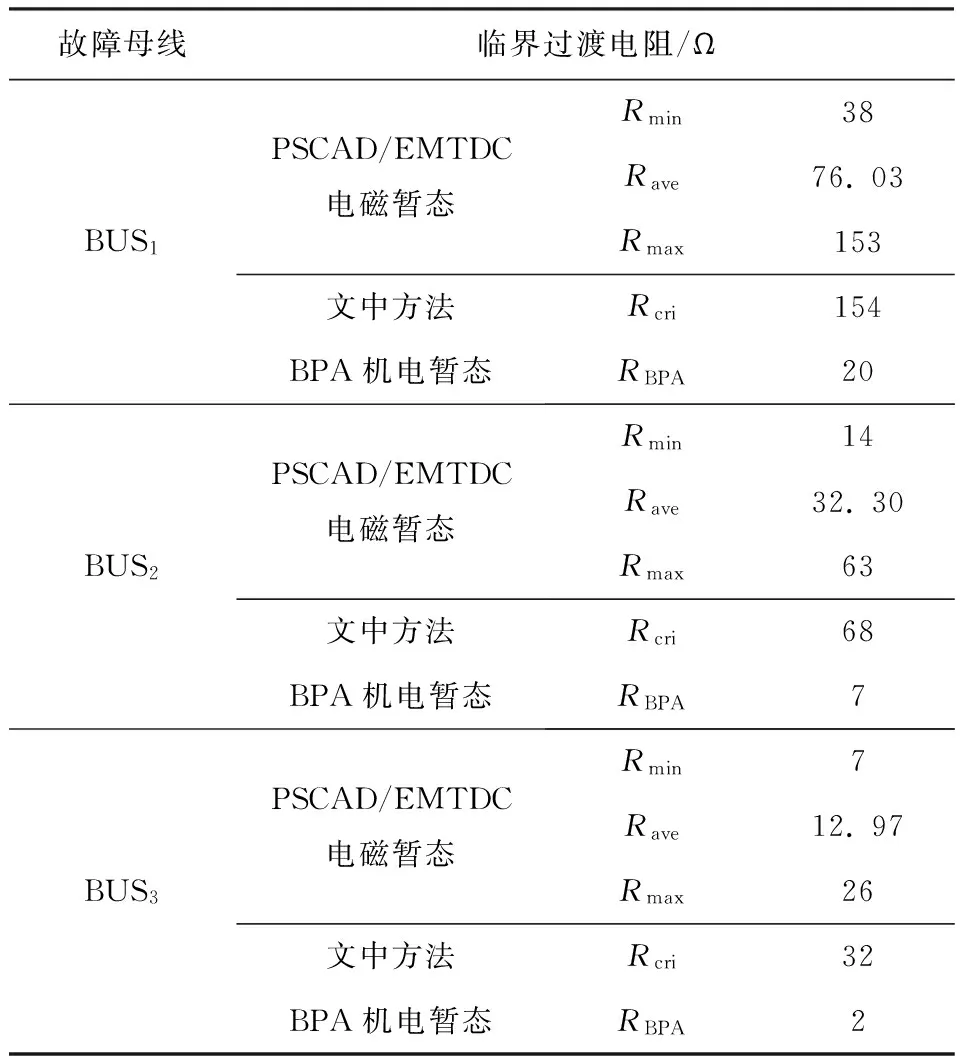
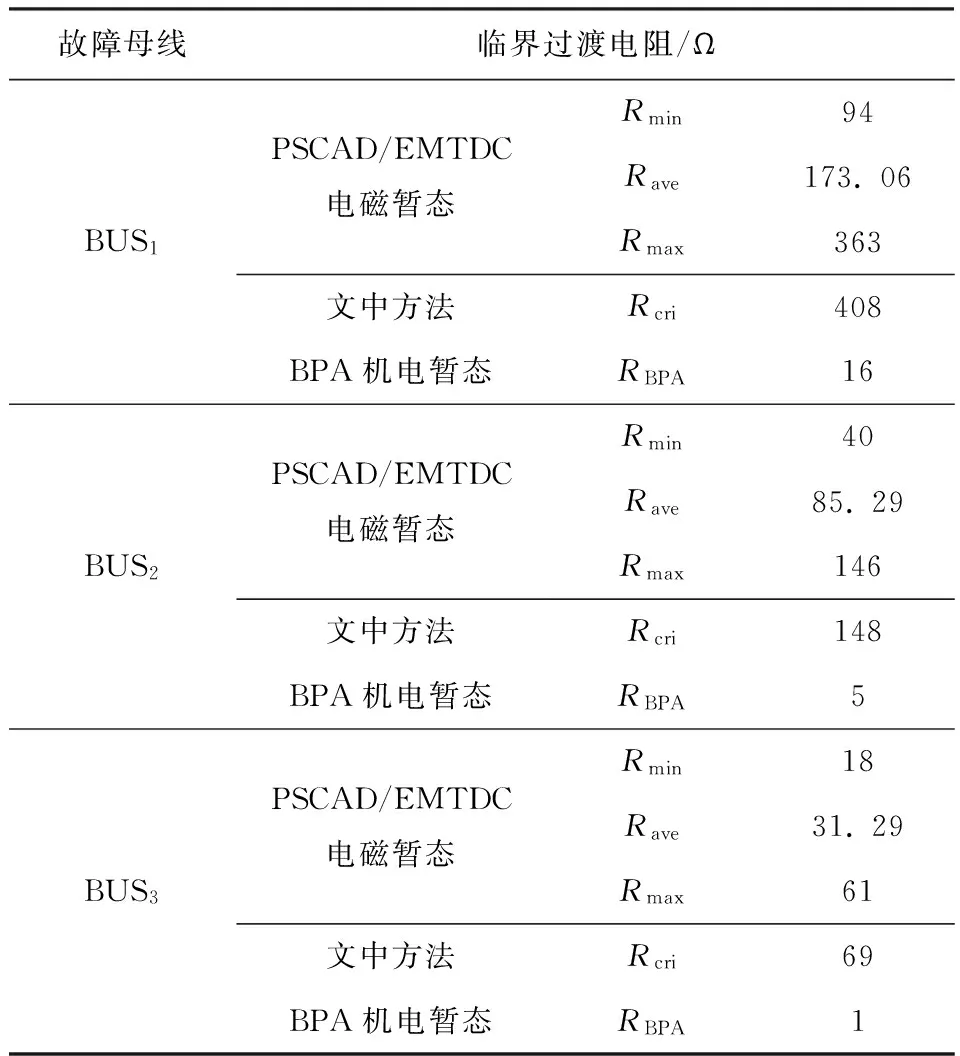
逆变侧交流故障下,换相电压随之发生变化.换相电压的幅值跌落与相位超前均将导致S减小,当减小至S 图1 十二脉波逆变器原理图 图2 故障合闸角对换相过程的影响 1)故障发生于时段I (3) 而当故障发生于tp2时,有 (4) 对比式(3)和式(4)可知,故障发生于时段I时,直流控制的作用将使得S增大,增加的换相电压时间面积如图2中ΔSΙ所示,有利于换相. 2)故障发生于时段Ⅱ 当故障时刻tⅡ∈(tp2,tp3)时,直流控制不对换相电压时间面积产生作用,故障时刻对换相电压时间面积的影响大小取决于tⅡ滞后于tp2的程度: (5) 对比式(4)和(5)可知,故障发生于时段Ⅱ时的S大于故障发生于触发脉冲时刻tp2的情况,增加的换相电压时间面积如图2中ΔSⅡ所示,说明该情况有利于换相,且故障时刻tⅡ越滞后越有利. 3)最不利换相的故障时刻 由1)和2)的分析可知,故障发生于时段I或者时段II时,所能提供的最大换相时间面积S均大于故障发生于脉冲触发时刻的情况,因此最不利于换相的故障时刻为故障相所对应的脉冲触发时刻. 换相失败的空间离散性是指交流系统不同位置的故障下,由于故障点与直流逆变站之间的稳态电压相位差和电气距离不同,直流是否发生换相失败存在差异.下文以三相故障为例,针对稳态电压相位差和电气距离的影响机理与规律加以分析. 交流站点k经过渡电阻Rf发生三相对称故障时系统可用图3等值电路表示.m点可为交流电网中任意节点,此处特指直流逆变母线.E1和E2为等值电路双侧电源,X1、Xm,k和X2分别为E1与m点、m点与k点、E2与k点之间的等值阻抗. 图3 交流站点k发生三相故障后的系统等值电路 (6) (7) 图4 故障后k点与m点线电压矢量图 Fig.4 Line voltage vector diagrams of buskand busmafter fault 首先分析故障点k和直流逆变站m之间稳态电压相位差对换相失败的影响机理. 1)故障前k点电压滞后于m点 2)故障前k点电压超前于m点 根据1)和2)的分析,故障点相位超前比相位滞后更有利于换相. 下面分析故障点k和直流逆变站m之间电气距离对换相失败的影响机理.由图4(a)和4(b)还可知,m点离k点越近,m点的故障后电压变化越显著;当m点与k点重合时,故障发生于逆变站,这是最不利于直流换相的故障位置. 根据以上分析还可知,换相失败的空间离散性不仅体现于不同位置交流故障下换流母线电压幅值变化的差异,还体现于电压相位变化的差异. 在BPA等机电暂态仿真软件中,熄弧角的计算基于式(8)实现: (8) 式中,Uac为逆变母线电压幅值,T为换流变压器变比,XC为换相电抗. 显然,式(8)只考虑了换相电压幅值,没有计入换相电压相位变化给熄弧角带来的影响,更没有考虑不同故障合闸角的情况,因而精度不高. 为实现换相失败的有效评估,文中提出一种新的熄弧角解析判据.该判据同时计及幅值和相位因素,较为准确地刻画了故障后电压的变化情况,更加全面地考虑了换相失败的影响因素,具体如下. 稳态下直流电流的表达式为 (9) 式中,Uac[0]为故障前逆变母线线电压幅值;β0为故障前的超前触发角;γ0为故障前的熄弧角. 由于直流控制器的响应变化需要一定的时间,所以故障后短期内认为β0不变.仿照式(9)推导过程,故障后还未发生换相失败时,有: cos(γf-Δφu)] (10) 式中,Uac[1]为故障后逆变母线线电压幅值;Δφu为故障后换流母线线电压前移的角度;γf为故障后的熄弧角. 若交流故障后未发生换相失败,此时的直流系统可以近似等值为恒定电流源,即Id[1]=Id[0].联立式(9)和式(10)求得熄弧角解析式: (11) 然而若交流故障后发生了换相失败,直流电流变化较明显,则该方法会出现较大误差. 1)故障较为严重时,电压变化较大,可能在β持续时间内换相过程未结束.此时,式(10)不成立.若仍用式(11)进行熄弧角计算,则因Uac[0]/Uac[1]和|Δφu|都比较大,γf的取值可能不正常:M>1,此时arccosM无解,γf无解;或者M≈1,此时arccosM≈0,即γf≈Δφu,故γf<0或γf较大. 2)故障较为轻微时,电压变化较小,此时换相失败表现为阀承受反向电压期间未恢复阻断能力而被倒换相,式(10)仍然成立.由于式(11)中Uac[0]/Uac[1]和|Δφu|都较小,可以保证M<1,但忽略直流电流变化将导致M减小,即γf增大.在直流处于换相失败的边界时,可能判断为换相成功. 根据1)和2)的分析,当熄弧角γf∈[0,γmin]或者取值不正常时,均可判别直流发生了换相失败;当熄弧角γf∈[γmin,γ0]时,可判别直流换相成功,误差仅出现在换相失败的边界.因此,由直流电流变化带来的误差基本不影响该式用于判别换相失败的有效性. 根据第1.1节,不考虑换流母线电压的变化滞后于故障点电压时,最不利于换相的故障时刻为触发脉冲发生时刻.结合以上分析可知,文中判据相当于计算换流母线电压变化瞬间的熄弧角,也即认为故障瞬间触发脉冲发出,因此其结果对应于不同故障合闸角下熄弧角离散区间的下边界. 结合第2.1节提出的熄弧角判据(式(11))和短路计算程序,可以快速实现交直流互联电网中发生交流故障时直流的换相失败判别,适用于任意直流、故障位置和故障类型.在给定故障下针对给定直流进行换相失败判别的具体步骤如下. 步骤1 获取给定直流逆变母线线电压、熄弧角和超前触发角的故障前稳态值,分别对应于式(11)中Uac[0]、γ0和β0. 步骤2 在短路计算程序中设置相应的故障位置、故障类型和过渡电阻,得到故障后的换流母线电压幅值Uac[1]和相位偏移Δφu. 步骤3 将上述参数相应地代入式(11),得到故障后的熄弧角γf,通过比较γf和临界熄弧角γmin的大小来判别直流是否换相失败.当且仅当γf∈[γmin,γ0]时,判定直流未发生换相失败. 综合以上分析,文中提出的评估方法不依赖于PSCAD/EMTDC中对于直流的详细建模与仿真,具备BPA在仿真效率和电网规模方面的优点,而且由于同时计及电压幅值和相位变化的影响,计算结果比BPA机电暂态软件等单独考虑电压幅值因素的方法更为精确. 文中分别在PSCAD/EMTDC和BPA仿真平台上搭建如图5所示的单直流带交流环网系统.其中,直流系统参数为云广直流输电系统的实际运行参数,而受端交流电网为“△”形结构,以模拟实际直流受端的环形主网. 图5 单直流带交流环网仿真模型示意图 Fig.5 Schematic diagram of the simulation model of single DC transmission with AC looped network 图5中,E0为整流侧的等值电源,Ebus2和Ebus3分别为接于母线BUS2和BUS3的等值电源;Z00、Z20和Z30为各电源与母线之间的等值阻抗;Z12、Z13和Z23为各母线之间的等值阻抗;P1+jQ1和P2+jQ2则分别为接入BUS1和BUS2的负载. PSCAD/EMTDC电磁暂态仿真程序包含有详细的直流系统电磁暂态模型,能够精确模拟换流器的电磁暂态过程并准确判别直流换相失败,因此可以用来验证文中所提出的换相失败评估方法的准确性.首先,在PSCAD/EMTDC中,分别在母线BUS1-BUS3处设置三相接地、单相接地、两相接地和相间故障,并相应地改变故障合闸角.根据对称性,三相对称故障的合闸角只需扫描60°,而不对称故障则需要扫描180°.以阀电流为判别换相失败的依据,不断调节过渡电阻大小进行仿真,得到各种故障条件下的临界过渡电阻.分析仿真结果,得到BUS1、BUS2和BUS3处不同类型故障位置和故障时刻时的临界过渡电阻的最大值Rave、最小值Rmin和平均值Rave. BPA机电暂态仿真程序包含有直流系统的准稳态模型,虽然无法准确地反映换流器的电磁暂态过程和判别换相失败,但由于其仿真效率高,目前在工程实际中得到广泛使用.为了验证文中所提换相失败评估方法相对于BPA的优势,同样地,在BPA中母线BUS1-BUS3处设置上述4种故障,利用BPA机电暂态程序的熄弧角仿真得到不同故障条件下的临界过渡电阻RBPA. 将文中方法的计算结果Rcri与上述两个模型的仿真结果进行对比,三相接地、单相接地、两相接地和相间故障的结果分别如表1至表4所示. 表1 三相接地故障下不同方法的评估结果 Table 1 Assessment results of three phase earth fault via diffe-rent methods 故障母线临界过渡电阻/ΩBUS1PSCAD/EMTDC电磁暂态文中方法BPA机电暂态Rmin41Rave76.45Rmax100Rcri87RBPA23BUS2PSCAD/EMTDC电磁暂态文中方法BPA机电暂态Rmin29Rave40Rmax49Rcri40.18RBPA9BUS3PSCAD/EMTDC电磁暂态文中方法BPA机电暂态Rmin10Rave14.09Rmax17Rcri18RBPA4 表2 单相接地故障下不同方法的评估结果 Table 2 Assessment results of single phase earth fault via diffe-rent methods 故障母线临界过渡电阻/ΩBUS1PSCAD/EMTDC电磁暂态文中方法BPA机电暂态Rmin31Rave57.81Rmax121Rcri171RBPA金属性故障下不发生换相失败BUS2PSCAD/EMTDC电磁暂态文中方法BPA机电暂态Rmin10Rave23.87Rmax47Rcri72RBPA金属性故障下不发生换相失败BUS3PSCAD/EMTDC电磁暂态文中方法BPA机电暂态Rmin4Rave9.39Rmax20Rcri34RBPA金属性故障下不发生换相失败 表3 两相接地故障下不同方法的评估结果 Table 3 Assessment results of two phase earth fault via diffe-rent methods 故障母线临界过渡电阻/ΩBUS1PSCAD/EMTDC电磁暂态文中方法BPA机电暂态Rmin38Rave76.03Rmax153Rcri154RBPA20BUS2PSCAD/EMTDC电磁暂态文中方法BPA机电暂态Rmin14Rave32.30Rmax63Rcri68RBPA7BUS3PSCAD/EMTDC电磁暂态文中方法BPA机电暂态Rmin7Rave12.97Rmax26Rcri32RBPA2 表4 两相相间故障下不同方法的评估结果 Table 4 Assessment results of two-phase phase to phase fault via different methods 故障母线临界过渡电阻/ΩBUS1PSCAD/EMTDC电磁暂态文中方法BPA机电暂态Rmin94Rave173.06Rmax363Rcri408RBPA16BUS2PSCAD/EMTDC电磁暂态文中方法BPA机电暂态Rmin40Rave85.29Rmax146Rcri148RBPA5BUS3PSCAD/EMTDC电磁暂态文中方法BPA机电暂态Rmin18Rave31.29Rmax61Rcri69RBPA1 由表1-4可知,母线BUS1、BUS2和BUS3故障下,文中方法得到的临界过渡电阻Rcri均较接近于PSCAD/EMTDC仿真所得临界过渡电阻的最大值Rmax,说明文中方法考虑了换相失败时间离散特性的保守边界情况,从而验证了文中方法的准确性,即文中方法考虑了最不利于换相失败的故障时刻,所得的评估结果偏于保守.而BPA机电暂态计算的熄弧角仿真得到的结果RBPA则明显与PSCAD/EMTDC的仿真结果相差较远,说明采用BPA仿真来评估直流换相失败,其评估结果准确性较低.以表1中母线BUS3发生三相对称故障为例,PSCAD/EMTDC仿真得到的临界过渡电阻区间为[10,17]Ω,而文中方法和BPA机电暂态仿真的熄弧角结果分别为18 Ω和4 Ω.根据以上分析,文中方法与PSCAD/EMTDC仿真的一致性远高于单独考虑电压幅值影响的BPA机电暂态仿真结果,文中方法具有更高的准确性并且兼顾了评估效率. (1)故障合闸角影响着换相电压所能提供的最大换相电压时间面积的大小,因此换相失败具有时间离散性;最不利于换相的故障时刻为故障相所对应的脉冲触发时刻. (2)故障点与逆变母线之间的稳态电压相位差和电气距离影响着换相电压的变化情况,从而导致换相失败的空间离散性;当电气距离越近、故障点相位越滞后时,交流故障越不利于换相. (3)考虑时空离散性的换相失败评估方法考虑了换相失败的时空离散性,可评估电网中任意位置、类型的故障发生于最不利时刻下直流换相失败的情况,兼具BPA仿真与PSCAD/EMTDC仿真的优点,准确性高,实用性强. [1] 张尧,林凌雪,钟庆.HVDC换相失败小波故障诊断方法 [J].华南理工大学学报(自然科学版),2007,35(10):172- 177. ZHANG Yao,LIN Ling-xue,ZHONG Qing.Fault diagnosis based on wavelet for commutation failures in HVDC [J].Journal of South China University of Technology(Natural Science Edition),2007,35(10):172- 177. [2] 邵瑶,汤涌.多馈入交直流混合电力系统研究的综述 [J].电网技术,2009,33(17):24- 30. SHAO Yao,TANG Yong.Research survey on multi-infeed AC/DC hybrid power systems [J].Power System Technology,2009,33(17):24- 30. [3] 王晶,梁志峰,江木,等.多馈入直流同时换相失败案例分析及仿真计算 [J].电力系统自动化,2015(4):141- 146. WANG Jing,LIANG Zhi-feng,JIANG Mu,et al.Case analysis and simulation of commutation failure in multi-infeed HVDC transmission systems [J].Automation of Electric Power Systems,2015(4):141- 146. [4] 袁阳,卫志农,雷霄,等.直流输电系统换相失败研究综述 [J].电力自动化设备,2013,33(11):140- 147. YUAN Yang,WEI Zhi-nong,LEI Xiao,et al.Survey of commutation failures in DC transmission systems [J].Electric Power Automation Equipment,2013,33(11): 140- 147. [5] 李新年,易俊,李柏青,等.直流输电系统换相失败仿真分析及运行情况统计 [J].电网技术,2012,36(6):266- 271. LI Xin-nian,YI Jun,LI Bai-qing,et al.Simulation analysis and operation statistics of commutation failure in HVDC transmission system [J].Power System Technology,2012,36(6):266- 271. [6] 刘俊磊,王钢,李海锋,等.HVDC系统换相失败对交流电网继电保护影响的机理分析 [J].中国电机工程学报,2013,33(19):111- 118. LIU Jun-lei,WANG Gang,LI Hai-feng,et al.Mechanism analysis of HVDC commutation failure influence on AC power metwork relay protection [J].Proceedings of the CSEE,2013,33(19):111- 118. [7] 夏成军,黄浩宇,涂亮,等.多馈入直流系统受端故障的协调渐进恢复策略 [J].华南理工大学学报(自然科学版),2016,44(4):47- 54. XIA Cheng-jun,HUANG Hao-yu,TU Liang, et al.Coordinated and progressive recovery strategy for failure at receiving end of Multi-infeed DC Systems [J].Journal of South China University of Technology(Natural Science Edition),2016,44(4):47- 54. [8] 欧开健,任震,荆勇.直流输电系统换相失败的研究(一)——换相失败的影响因素分析 [J].电力自动化设备,2003,23(5):5- 8. OU Kai-jian,REN Zhen,JIUG Yong.Research on commutation cailure in HVDC transmission systems part 1:commutation failure factors analysis [J].Electric Power Automation Equipment,2003,23(5):5- 8. [9] 吴萍,林伟芳,孙华东,等.多馈入直流输电系统换相失败机制及特性 [J].电网技术,2012,36(5):269- 274. WU Ping,LIN Wei-fang,SUN Hua-dong,et al.Research and electromechanical transient simulation on mechanism of commutation failure in multi-infeed HVDC power transmission system [J].Power System Technology,2012,36(5):269- 274. [10] 何朝荣,李兴源.影响多馈入高压直流换相失败的耦合导纳研究 [J].中国电机工程学报,2008,28(7):51- 57. HE Chao-rong,LI Xing-yuan.Study on mutual admittance and commutation failure for multi-infeed HVDC transmission systems [J].Proceedings of the CSEE,2008,28(7):51- 57. [11] 刘健,李兴源,傅孝韬.多馈入短路比及多馈入交互作用因子与换相失败的关系 [J].电网技术,2009,33(12):20- 25. LIU Jian,LI Xing-yuan,FU Xiao-tao.Relationship of multi-infeed short circuit ratio and multi-infeed interaction factor with commutation failure [J].Power System Technology,2009,33(12):20- 25. [12] 邵瑶,汤涌,郭小江,等.2015年特高压规划电网华北和华东地区多馈入直流输电系统的换相失败分析 [J].电网技术,2011,35(10):9- 15. SHAO Yao,TANG Yong,GUO Xiao-jiang,et al.Analysis on commutation failures in multi-infeed HVDC transmission systems in North China and East China power grids planned for UHV power grids in 2015 [J].Power System Technology,2011,35(10):9- 15. [13] 陈政,周保荣,洪潮,等.基于临界阻抗边界的多馈直流系统同时故障风险评估 [J].电网技术,2013,37(3):874- 878. CHEN Zheng,ZHOU Bao-rong,HONG Chao,et al.Critical impedance boundary-based risk assessment on simultaneous faults in multi-infeed DC transmission system [J].Power System Technology,2013,37(3):874- 878. [14] 邵瑶,汤涌.采用多馈入交互作用因子判断高压直流系统换相失败的方法 [J].中国电机工程学报,2012,32(4):108- 114. SHAO Yao,TANG Yong.A commutation failure detection method for HVDC systems based on multi-infeed interaction factors [J].Proceedings of the CSEE,2012,32(4):108- 114. [15] 肖浩,朱佳,李银红,等.多馈入直流系统换相失败免疫水平快速确定方法研究 [J].中国电机工程学报,2015,35(11):2711- 2717. XIAO Hao,ZHU Jia,LI Yin-hong,et al.Study on rapid determination method of commutation failure immunity levels for multi- infeed HVDC transmission systems [J].Proceedings of the CSEE,2015,35(11):2711- 2717. [16] BAUER T,LIPS H.P,THIELE G,et al.Operational tests on HVDC thyristor modules in a synthetic test circuit for the sylmar east restoration project [J].IEEE Transactions on Power Delivery,1997,12(3):1151- 1158. [17] 罗龙波.高压直流输电系统换相失败时间离散性研究 [D].广州:华南理工大学,2013. [18] 任震,陈永进,梁振升,等.高压直流输电系统换相失败的概率分析 [J].电力系统自动化,2004,28(24):19- 22. REN Zhen,CHEN Yong-jin,LIANG Zhen-sheng,et al.Probabilistic analysis of commutation failures in HVDC transmission systems [J].Automation of Electric Power Systems,2004,28(24):19- 22. [19] 洪潮.直流输电系统换相失败和功率恢复特性的工程实例仿真分析 [J].南方电网技术,2011,5(1):1- 7. HONG Chao.Simulation analysis on the commutation failure and power recovery characteristic of an actual DC transmission system [J].Southern Power System Technology,2011,5(1):1- 7. [20] 王钢,李志铿,黄敏,等.HVDC输电系统换相失败的故障合闸角影响机理 [J].电力系统自动化,2010(4):49- 54. WANG Gang,LI Zhi-keng,HUANG Min,et al.Influence of initial fault voltage angle on commutation failure identification in a HVDC system [J].Automation of Electric Power Systems,2010(4):49- 54. [21] THIO C V,DAVIES J B,KENT K L.Commutation failures in HVDC transmission systems [J].IEEE Transactions on Power Delivery,1996,11(2):946- 957. AMethodtoAssessCommutationFailureofHVDCSystemsTakingSpace-TimeDiscretenessintoConsideration CAIZe-xiangYANGHuan-huanYUChao-yunLIXiao-hua (School of Electric Power, South China University of Technology, Guangzhou 510640, Guangdong, China) As the characteristics of commutation failure of high-voltage direct current (HVDC) systems vary with not only fault close angle but also fault positions, the existing assessment methods that only consider the influence of voltage dip of converter bus are not accurate enough. In order to solve this problem, firstly, the space-time discreteness of commutation failure is investigated. Secondly, the influence of fault close angle on the process of commutation failure is analyzed, and the most unfavorable angle is pointed out. Then, two main causes for the impact of fault position on commutation failure, namely the electrical distance and the phase difference between fault bus and DC inverter bus, are discovered. Moreover, in light of the analytical results of space-time discreteness under the condition of commutation failure, a criterion of extinction angle, which takes both voltage amplitude and phase distortion into consideration, is proposed. Thus, a method to assess commutation failure is presented. Finally, a comparison of the proposed method is made with PSCAD/EMTDC and BPA on a three-node AC/DC system in China Southern Power Grid. The results show that the proposed method is effective and practicable. high-voltage direct current; commutation; space-time discreteness; voltage amplitude; phase change; extinction angle; assessment method 2016- 08- 02 国家自然科学基金资助项目(51377059) *Foundationitem: Supported by the National Natural Science Foundation of China(51377059) 蔡泽祥(1960-),男,教授,博士生导师,主要从事电力系统保护、控制与自动化研究.E-mail:epzxcai@scut.edu.cn 1000- 565X(2017)07- 0033- 08 TM 711 10.3969/j.issn.1000-565X.2017.07.005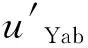
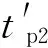
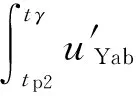
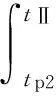
1.2 换相失败的空间离散性
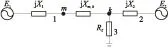
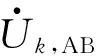
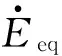
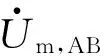
2 考虑时空离散性的换相失败评估方法
2.1 计及电压幅值与相位变化的熄弧角判据
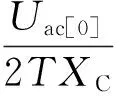
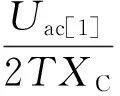
2.2 基于短路计算程序的换相失败评估方法
3 算例分析
3.1 研究系统
3.2 换相失败评估方法校验

4 结论
