复杂环境下蓝牙定位模型优化方法研究

， ，，，

(1.苏州科技大学 江苏省建筑智慧节能重点实验室，江苏 苏州 215009；2.苏州市移动网络技术与应用重点实验室，江苏 苏州 215009；3.苏州科技大学 电子与信息工程学院，江苏 苏州 215009)

复杂环境下蓝牙定位模型优化方法研究

罗恒1,2,3，张昱3，邹优敏3，傅启明1,2,3，刘垒垒3

(1.苏州科技大学江苏省建筑智慧节能重点实验室，江苏苏州215009；2.苏州市移动网络技术与应用重点实验室，江苏苏州215009；3.苏州科技大学电子与信息工程学院，江苏苏州215009)

社会经济以及移动网络技术的快速发展，使得室内定位需求大幅度增长;但是，建筑结构等因素导致普遍使用的全球定位系统GPS在室内定位中性能急剧下降，不能很好满足室内定位的需要;针对各类复杂室内环境，提出了基于环境参数校准的自适应信号强度优化算法;从理论上分析了高斯滤波的性能，使用蓝牙4.0技术，以锚节点作为参考节点，采用均值滤波和高斯滤波优化RSSI值校准基准信号，运用线性规划实时、动态估算环境衰减系数，分析了改进基准信号模型和改进衰减系统模型的性能，最后获得信号传输综合优化模型;使用计算机仿真及实验方式对算法进行了研究，实验结果表明，在复杂办公室环境下，定位误差绝对值小于1 dbm，定位误差小于2%，能够较好地满足室内定位的需求。

蓝牙定位；参数校准；线性规划；RSSI

0 引言

全球定位系统GPS(global positioning system,GPS)[1]的产生及发展，为相关人员提供了在广阔的室外空间中精确获得特定物体地理位置的可能。GPS已经在军事[2]、资源[3]、交通、农牧渔业[4]、环境[5]和测绘[6]等领域获得了非常广泛的应用。然而，面对复杂的室内环境，GPS定位精确度急剧下降[7]，不能很好地满足室内定位需求。

据不完全统计，人类有80%以上的时间在室内度过[8]。由于室内空间越来越庞大复杂，室内定位变得越来越困难。如在博物馆、超市、机场等场所[9]，消费者需要快速了解自身所处位置,并到达目的地；在矿井、火灾等现场，救援人员也需要获取被困者的精确位置。室内定位的需求前所未有得高涨。面对需求的增加，室内定位的市场也逐步扩大。

1 室内定位技术

室内定位技术的提出可以追溯到上世纪，经历了不同的发展阶段。

1.1 红外定位技术

1992年，Want等人提出了一种主动红外定位系统[10]。每个目标节点携带一个红外发射标签，同时在特定办公区域安装接收传感器，实时感知目标节点在办公区域中的不同位置。由于系统的简便性，在当时获得了较为广泛的应用。该系统的主要缺点是定位准确性受到诸如自然光、照明系统等环境因素隐私较大。

1.2 超声波定位技术

AT&T公司于1997年推出了一款先进的Active Bat超声波定位系统[11]，通过模仿蝙蝠的定位原理，获得目标位置。通过安装3个或者多个接收天线，获取超声波反射信号，基于三边定位算法，预估目标位置。实验结果表明，Active Bat系统可以同时定位多个目标，其可达到厘米级定位精度。

1.3 基于图形信息的定位技术

基于图形信息的定位技术可分为主动式和被动式方法两种，其分类依据为摄像头安装位置。被动式定位主要利用安装在定位目标上的摄像头，实时获取目标位置，其典型应用为SignPost[12]；主动式定位技术主要依赖安装在环境中的摄像头，利用图像处理技术，获取目标位置，其典型代表为微软公司研究院发布的EasyLiving[13]。

1.4 基于射频技术的定位方法

当前，常用的视频室内技术方法包含WiFi、RFID和蓝牙等。

WiFi具备规模大、覆盖范围广的优点，但是，WiFi的发射功率大，能耗大导致应用成本较高。RFID定位技术具有快速精确定位、传输范围较大、成本亦较低等优点，现有移动设备中的整合一直是RFID的一大缺点。蓝牙具有成本低、功耗低的优点，且与现有移动终端融合程度较好，然而定位精度一直是蓝牙定位面临的问题。

2013年，Oguejiofor团队给出了一种基于位置信息的盲节点定位算法[14]。该算法依据各节点获得的RSSI信号强度，动态估计某个目标节点的具体位置。实验结果表明，算法的精确度主要依赖于锚节点的个数。当锚节点从3个增加到4个时，定位精度可以提高约24%。

Ranron团队通过使用基于ZigBee的RSSI指纹定位技术[15]，实现了人员室内定位，实验结果表明，当定位距离约为3米时，误差约为0.77米。

2014年，Oliveira Luis团队给出了一种稀疏锚节点相对定位算法[16]，旨在实现多目标定位。通过节点间的交互信息的分析，实时获取两两目标节点间的距离，算法通过卡尔曼滤波和Floyd-Warshall算法实现了目标位置的精确定位。

Grossmann, U.团队分析了最小欧几里得距离和贝叶斯随机过程模型在室内定位中的性能[17]，提出了一种基于WiFi信号RSSI强度的室内定位算法。在空旷的演讲室中的实验表明了该算法的可行性，同时，Grossmann, U.团队也给出了该系统在博物馆应用中应注意的事项。同年，Y.H. Gu团队提出了一种利用RFID技术实现室内定位的方法[18]，与K最近邻节点算法与自纠错算法相比较，该算法具有更高的定位精度。

2015年，Su, Hui-Kai团队提出了一种基于蓝牙和WiFi的多技术混合定位方法[19]，实验结果表明，混合定位算法结合邻节点权重定位方法，比使用单一技术的定位方法，具有明显的优越性，当锚节点合理部署情况下，定位精度可以降低至0.4米。

针对蓝牙在室内复杂环境定位精度的问题，陶为戈团队[20]提出一种基于最小二乘法估算环境参数的算法，优化了信号的传播模型。本文从监督学习的角度提出了一种电磁波自由传播衰减系数自适应模型，通过自适应调整衰减模型以适应不同室内环境下的定位。除此之外，M.D. Wang团队还提出了基于超宽带技术的室内定位技术。

2 优化算法

在理想电磁波自由空间传播模型中，电磁波的传播满足：

p(d)=p(d0)-10nlg(d)+ζ

(1)

其中：p(d)为远离基站d米处的信号强度，p(d0)为远离基站d0米处的信号强度，二者的单位均为dBm；n表征无线信道衰减系数，n的取值与距离无关，仅与环境因素相关；ζ表示噪声的影响，其取值服从均值为零的高斯分布。

不妨设p(d0)为一个固定值，即p(d0)=A，RSSI为实际环境下远离基站d米处的电磁波信号强度，即p(d)=RSSI，则式(1)可写为：

RSSI=A-10nlg(d)+ζ

(2)

在实际应用中，为了降低计算的复杂度，通常情况下A为设备制造商提供的固定参考值；n为如表1所示的经典经验值。

在简单的室内环境下，由于环境因素相对恒定，这一假设具有一定合理性。然而，在复杂的室内环境下，障碍物、电子设备的电气特性和噪声等因素使得电磁波传播呈现出明显的时变特性，其结果是基于电磁波信号强度的室内定位系统精度大幅度下降，不能很好地满足实际应用需求。针对这一情况，本文拟对信号基准强度参考值A和环境衰减系数n分别优化，获取复杂室内环境下电磁波传输最优化模型。

2.1 基准信号A优化

基准信号强度A是定位模型中的一个重要参量，与定位精度具有很大的相关性，通常取d0米处的平均值作为参考值。在不采用设备制造商使用的参考值时，若样本空间足够大，信号强度RSSI可以通过样本的数学平均获取。然而，当样本空间有限时，取样本的数学平均这种方法会产生较大误差，误差来源主要包括噪声的影响、电磁波的时变传播特性等。

相关研究表明，在距离发射基站d处的RSSI均服从均值为μ，方差为σ2的高斯分布，当d=d0时，信号强度的概率密度函数为：

P(RSSId0) =

(4)

其中，RSSId0,k表示d0处共计j个信号强度中的第i个信号强度。

RSSId0在区间[μ-σ，≤μ+σ]中的概率为：

P(μ-σ≤RSSId0<μ+σ)=F(μ+σ)-F(μ-σ)

=φ(1)-φ(-1)=2φ(1)

(5)

其中：

(6)

(7)

根据式(5)计算得P(μ-σ≤RSSId0<μ+σ)=0.6826，所以，区间[μ-σ,μ+σ]为高概率发生区。

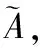
(8)

其中：β表示d0处经过高斯滤波后的信号强度的个数，RSSId0,k表示d0处β个信号强度中的第k个信号强度。

2.2 衰减系数n优化

选定l个锚节点，令锚节点到参考节点M的距离分别为d1，d2，d3，…，dl，在办公、家居等室内环境下，由于空间关系，可认为节点处于同一环境之中，假设它们具有相同的信号传输特性，则可根据：

(9)

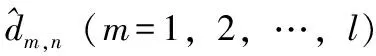
(10)

其中：RSSIi表示实际距离di处的信号强度；αm(m=1,2,…,l)为Δdm,n的系数。基于式(9)中的线性规划，可获得Δdn的最小值，此时的n值即为当前环境的最优化衰减系数。

3 实验及结果分析

3.1 测试环境及参数设置

图1所示为算法的测试环境，如图所示，测试环境中主要存在浅色与深色两种主要的障碍物，其材质分别为为木质台面和金属质边框。

图1 办公室环境

表2所示为实验参数，其中蓝牙基站发射功率为1 mW，从0 m开始每隔0.1米采集一组数据，采样间隔为1 s，基站与物体表面距离为1米，模拟手持移动设备实际高度，同时降低地面反射及噪声等的影响。

图2所示为采样点对结果的影响程度，如图所示，当采样点为100时，预测的信标位置分散在实际位置周围，呈现出发散的特性；当采样点数量增加至400时，平均后的预测值明显集中；随着采样点数量的进一步增加，平均后的预测位置与实际位置误差明显减少；当采样点数量突破1 000后，采样点数量对平均后的预测值维持恒定。综上所述，采样点数量大于1 000，平均结果可以较好地满足后续分析需求。为保证更高的精度，算法使用2 000个采样点的平均值。

图2 采样点数量的影响

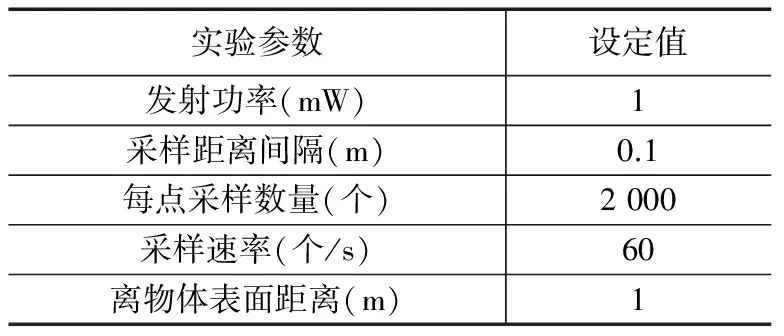
表2 具体参数设置

3.2 结果及分析

图3所示为使用不同优化模型得到的预测值与实际值的对比结果。由图可见，从误差绝对值角度而言，当定位节点与定位锚节点距离增加到2米时，基准信号模型预测误差从6 dbm下降到5 dbm，改进衰减系数n模型预测误差从6 dbm快速下降到0.1 dbm左右，呈现出良好的预测结果，改进基准信号模型预测结果呈现上升趋势，预测误差从0 dbm逐步上升至2.3 dbm。 从误差相对值角度观察，误差相对值变化特征与绝对值变化特征一致，区别主要在于误差相对值下降或者上升的速率大，造成这一现象的主要原因是实际距离数值较小。综上所述，当测量结果与基准锚节点距离不超过2米时，理想自由空间模型性能最差，改进衰减系数模型性能优于理想自由空间模型，而改进基准信号模型性能最优。

当信标节点与锚节点距离从2米增加到3米时，理想自由空间模型预测结果误差呈现出线性增长的特性，改进衰减系数模型预测绝对误差呈线性下降趋势，从2 dbm逐步下降至0.8 dbm，改进衰减系数模型误差性能最优，保持在0.2 dbm以下。从相对误差角度而言，当距离从2米增加至3米时，理想自由空间模型的预测误差从10%上升至15%，表明性能继续恶化。虽然改进基准信号模型在此区域内误差性能有所改善，但是其改善程度仍远远高于改进衰减系数模型。总之，当实际距离介于2米至3米区间时，改进衰减系数模型仍然表现出优良的性能。

当测量节点与锚节点距离进一步增加，即从3米增加到8米时，理想自由空间模型和改进基准信号模型预测误差基本都呈现出线性增加的特性，改进衰减系数模型的预测误差具有震荡特点。随着实际距离增加到5米，改进衰减系数模型产生的误差也逐渐增加，在达到区域极值后，快速下降，当实际距离为6米时，无论是相对误差和绝对误差，都接近于0,，随着距离的继续增加，误差再次呈现增加-减少的特性。由上述分析可见，当实际距离大于3米时，理想自由空间模型性能依然最差，改进基准信号模型性能略好，改进衰减系数模型性能最佳，其相对误差保持在2%以下。

基于上述分析，可以构建模型综合，在距离小于2米时，使用基准信号优化模型；当距离逐渐增加到8米过程中，使用改进衰减系数n的优化模型。图3中实线所示即为综合模型，综合模型同时具有基准信号优化模型和衰减系数优化模型的优点，在性能上，综合模型的绝对误差小于1 dBm，相对误差小于2%。

图3 测量结果

4 结论

实验结果表明，综合了改进基准信号模型和改进衰减系数模型的综合模型优化了改进衰减系数模型在较近距离时误差较大的缺点，当距离增加时，可以动态获取衰减系数，保证了相对误差和绝对误差都处于较低的水平，从性能上来看，综合模型绝对误差最大值不超过1 dBm，相对误差低于5%，特别当距离从3米逐渐增加到8米过程中，衰减系数n优化模型性能较为突出，相对误差保持在2%以下。能够较好地满足室内定位对精度的要求。

综合算法立足于二维定位算法的实现与优化，成果可以为三维定位奠定良好的基础，是实现高精度三维定位的重要前提，具有非常重要的理论与现实意义。

[1]Zumberge J F, Heflin M B, Jefferson D C, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research Solid Earth, 1997, 102(B3):5005-5017.

[2]Lachow I. The GPS Dilemma: Balancing Military Risks and Economic Benefits[J]. International Security, 1995, 20(1):126-148.

[3]Nandini N, Jumbe A S, Tandon S, et al. Application of Remote Sensing, GIS, and GPS Technology on Environment and Earth's Natural Resources Management An Introduction[J]. 2007.

[4]Mundy C. Using GPS technology to improve fishery-dependent data collection in abalone fisheries[J]. Research, 2012.

[5]季 方, 鲍远律. 全球任意区域GPS定位环境分析[J]. 计算机仿真, 2006, 23(1):51-53.

[6]Zhao C Z. Application of GPS surveying and mapping technology in engineering mapping[J]. Heilongjiang Science, 2016.

[7]Ochiai M, Fujii M, Ito A, et al. A study on indoor position estimation based on fingerprinting using GPS signals[A]. International Conference on Indoor Positioning and Indoor Navigation[C]. IEEE, 2014:727-728.

[8]张 静. 室内空气污染现状分析与对策[J]. 大观周刊, 2012(6):280-280.

[9]曾 俊. 基于RFID的室内定位算法研究[D]. 成都：电子科技大学, 2015.

[10]Want R, Hopper A, Falco V, et al. The active badge location system[J]. ACM Transactions on Information Systems，1992(10):91-102.

[11] Ward A, Jones A, Hopper A. A new location technique for the active office[J]. IEEE Personal Communications，1997(4):42-47.

[12]Mulloni A, Wagner D, Barakonyi I, et al. Indoor positioning and navigation with camera phones[J]. IEEE Pervasive Computing, 2009(8): 22-31.

[13]Brumitt B, Meyers B, Krumm J, et al. EasyLiving: Technologies for Intelligent Environments[C]. Handheld and Ubiquitous Computing, Second International Symposium, HUC 2000, Bristol, UK, Proceedings. DBLP, 2000:12-29.

[14]Oguejiofor O, et al. Outdoor localization system using RSSI measurement of wireless sensor network[J]. International Journal of Innovative Technology and Exploring Engineering, 2013(2):1-6.

[15]Ranron, Ratchasak, Kamol Kaemarungsi, Implementation of zigbee localization using rssi location cluster[C]. Proc. ECTI-CARD 2013.

[16]Oliveira Luis, et al, RSSI-based relative localisation for mobile robots[J]. Ad Hoc Networks, 2014(13):321-335.

[17]Grossmann U, Gansemer S, Suttorp O. RSSI-based WLAN indoor positioning used within a digital museum guide[J]. International Journal of Computing, 2014(7):66-72.

[18]Gu Y, Ren F. Energy-Efficient Indoor Localization of Smart Hand-Held Devices Using Bluetooth[J]. IEEE Access, 2015(8):765-767.

[19]Su Huikai, et al. A hybrid indoor position mechanism based on bluetooth & WiFi communications for smart mobile devices[C]. International Symposium on Bioelectronics and Bioinformatics (ISBB),2015.

[20]陶为戈, 朱昳华, 贾子彦. 基于RSSI混合滤波和最小二乘参数估计的测距算法[J]. 传感技术学报, 2012, 25(12):1748-1753.

ResearchonBluetoothLocationModelOptimizationinComplexIndoorEnvironMent

Luo Heng1,2,3, Zhang yu2,3, Zou Youmin2, Fu Qiming1,2,3, Liu Leilei3

(1. JiangSu Province Key Lab of Intelligent Building Energy Efficiency, Suzhou 215009,China; 2.Suzhou Key Lab of Mobile Networking and Applied Technology, Suzhou 215009,China; 3.Suzhou University of Science and Technology, Suzhou 215009,China)

With the development of modern economy, society and mobile network technology, the requirements for indoor positioning for various applications are quite large and continue growing. Aiming at the complicated indoor environment, an adaptive signal strength optimization algorithm based on environmental parameter calibration is proposed, using the Bluetooth 4.0 technique. The mathematical analysis for the applications of Gaussian filter is provided. The RSSI value calibration reference signal is optimized by Gaussian filtering. Meanwhile, the linear attenuation coefficient is optimized adaptively by linear programming, leading to optimization of the propagation model of electromagnetic wave for Bluetooth. Simulation and Experiment results show that the error is less 1 dbm in absolute value and 2% in relative value in the complex office environment, which satisfies well the requirement for indoor positioning.

Bluetooth positioning; parameter calibration; linear programming; RSSI

2017-07-10；

2017-09-08。

国家自然科学基金项目(61602334，61502329，61401297)；住房与城乡建设部科学技术项目(2015-K1-047)；江苏省自然科学基金项目(BK20140283)。

罗 恒(1981-)，男，江苏苏州人，博士，讲师，主要从事人工智能理论与方法及其在建筑节能中的应用方向的研究。

1671-4598(2017)11-0244-04

10.16526/j.cnki.11-4762/tp.2017.11.062

TP393

A