基于ABC-NB的慢性病诊断分类研究
2017-12-15,
,
(浙江理工大学 信息学院,杭州 245000)
基于ABC-NB的慢性病诊断分类研究
王尚哲,张云华
(浙江理工大学信息学院,杭州245000)
在医疗领域,医生做出有效正确的决策非常重要,为了提高医生诊断的准确性,避免诊断结果受到医生的直觉、潜意识和自身知识不全面等因素的干扰而造成误判;提出了将改进的ABC-NB算法应用于慢性病诊断领域,以提高诊断效率,减少误判几率;将基于改进尺度因子的人工蜂群算法应用于慢性病特征的选择,对数据进行降维,剔除冗余、无关的特征,提高收敛速度,增强算法搜索全局最优解的能力;接着将预处理后的数据各特征值进行训练和学习生成贝叶斯分类器,构建预测模型;预测模块将诊断结果显示出来供医护人员参考,辅助进行诊断和决策;实验表明该模型具有很好的柔性和鲁棒性,能够稳定的计算出慢性病的概率,有效的辅助医护人员进行诊断。
慢性病诊断;特征选择;人工蜂群算法;朴素贝叶斯分类器
0 引言
长时间以来,慢性病一直是危害居民健康的因素之一,其具有病程长且无法治愈的特点,因此慢性病的提前发现与预防已逐渐成为我国乃至世界医护人员最关心的问题之一[1]。近些年,随着“互联网+”浪潮的不断推进,越来越多的医疗卫生信息系统在医院被使用,大量临床数据被存储在医疗数据库中,医疗数据呈现爆炸式的增长,各系统数据库所存储的相关医疗数据显得越发重要。但由于数据多以分散、不连续的形式存在,仅凭人工阅读的方式不足以从海量数据中分析出更多有用的信息。若能够运用现代计算机技术对各种数据进行筛选、分析,并提取出医生的临床经验以及疾病的诊断知识,构造一个辅助诊断模型,为医务人员提供服务和协助,则可以避免传统诊断过程中的主观判断,提高慢性病诊断的效率与准确率。
由于医院的医疗数据为海量的,其中存在很多不相关的特征属性,从大量的历史临床数据中发现有价值的信息为今后的疾病预测与诊断提供依据便成了首要任务[2]。特征选择是指选择产生最多预测结果的相关特征的问题,通过特征选择能剔除不相关或冗余的特征,保留有效特征,从而达到从原始数据集中得到最优子集的目的。在很多实际问题中,搜索和筛选特征变量并没有普适的方法,常见的算法启发式搜索的序列前向选择算法,其缺点是只增加特征值,不减少特征值;还有类似随机搜索策略的特征选择算法,缺点是当存在较多的特征数量时,算法在执行的过程中会耗用大量时间,实用性不高[3]。本文提出了一种人工蜂群优化算法进行特征搜索和选择。实验表明,该模型整体诊断率稳定在81%左右,有效提高了诊断效率。
1 蜂群算法进行特征选择
1.1 蜂群算法基本原理
人工蜂群算法(artificial bee colony, ABC)是由Karaboga于2005年提出的一种新颖的基于群智能的全局优化算法,是近几年比较热门的智能算法。蜂群算法是一种非数值优化算法,其直观背景来源于蜂群的采蜜行为,建立在蜜蜂自组织型与群体智能基础之上,蜜蜂通过蜂群的分工进行不同的行为,对传回蜂群的信息进行共享与交流,从而找到最优的蜜源[4-5]。
在一个真正的蜜蜂群落中,不同的任务有不同的专职蜜蜂执行,这些专门的蜜蜂尝试通过执行有效的分工以及对信息进行共享和交流,力求最大限度的找到最优解,即蜂蜜含量最高的蜜源。人工蜂群算法通过模拟自然界蜜蜂实际采蜜的行为将人工蜂群分为引领蜂、观察蜂和侦察蜂,引领蜂和观察蜂之间会根据蜜源的质量等因素进行角色切换,当引领蜂多次搜寻未找到质量有所改善的蜜源时,其角色变成侦察蜂放弃现有的蜜源,在蜂巢周围继续搜索新的蜜源。当寻找到质量有所改善的蜜源时,便切换角色又变为引领蜂。在人工蜂群算法中,蜂群分为数量相等而角色不同的两个群体,一半的蜂群为侦查蜂,另一半为观察蜂。被雇用的蜜蜂利用先前的蜜源信息寻找新的蜜源并与以前搜寻到的蜜源质量进行对比,然后向其他的观者蜂提供关于他们正在搜寻的蜜源质量以及位置的信息。等候在蜂巢周围的观察蜂根据侦查蜂传回的蜜源信息来决定一个蜜源是否开采。
1.2 蜂群算法的步骤
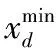
(1)
在搜索的阶段,引领蜂在相对应的第i个蜜源周围依据如下公式(2)寻找新的蜜源:
wid=xid+φ(xid+xkd);
(2)
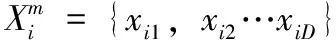

(3)
如果观察蜂依据引领蜂分享的信息去选择了蜜源i,同样也会据公式(2)在蜜源i周围产生一个新的蜜源,并根据贪婪选择法选择蜜源。在搜索过程中,fiti是可能解Xi的适应值。当在经过t次迭代后,所有的引领蜂和观察蜂都已搜索完整个空间,如果在到达阈值limit而蜜源的适应值没有被提高时,则丢弃该蜜源,而与该蜜源相对应的引领蜂切换角色变为侦查蜂,侦查蜂在搜索空间随机产生一个新的蜜源代替Xi,m为迭代次数,过程如公式(4)所示:
(4)
为保持普遍性和不失去一般性,解的适应度在蜂群算法中根据公式(5)进行评价计算。
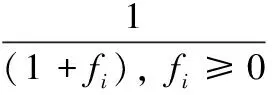
fiti=1+abs(fi),fi<0
(5)
将蜂群算法和其他的群体智能算法进行对比,根据蜜源的信息进行角色切换是其独有的机制[7]。蜂群在侦察蜂、跟随蜂和引领蜂3 类不同角色之间进行转换,通过共享信息协作寻找最优的蜜源。在 ABC 算法寻优的过程中,不同角色蜜蜂作用有所差别: 引领蜂用于维持优良解; 跟随蜂用于提高收敛速度; 侦察蜂用于增大跳出局部最优解的能力。蜂群搜寻最优蜜源的过程就是目标函数寻找全局最优解的过程。人工蜂群算法流程如图1所示。
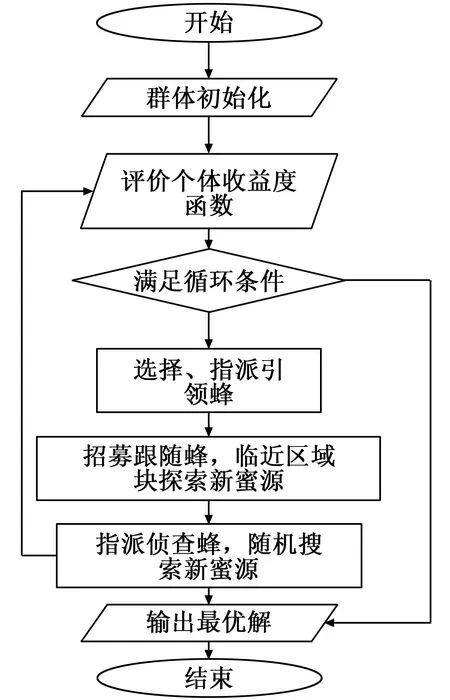
图1 人工蜂群算法流程
2 基于朴素贝叶斯网络的慢性病特征分类模型
2.1 朴素贝叶斯分类器
朴素贝叶斯分类是分类算法中较为简单且误差率很低的一种,贝叶斯是指基于贝叶斯定理,朴素指的是特征条件独立[8]。朴素贝叶斯的思想基础是这样的:求解给出的待分类项在各个类别中的概率,所得概率最大的类别就被认为是此待分类项所属的类别[9]。
对于一个求解分类的问题,根据贝叶斯定理,待分类样本x属于类别y的概率公式为:

(6)
在这里,x是一个特征向量,将x维度设为M。由于朴素贝叶斯分类算法中特征条件独立,上述公式可根据全概率公式展开表达为:

(7)
其中:yi∈{c1,c2…ck}属于K中的一类,类别分为两类(患病和不患病),只要分别估计出医院样本数据特征xi对应每一类上的条件概率就可以了。类别yi在所有类别中的概率可根据训练集计算得出,数据特征对应每个类别的条件独立概率向量同样可通过训练集统计得出。
2.2 学习(参数估计)
生成分类器是本阶段的主要工作,该阶段是机械性的,通过输入特征属性和训练样本,计算训练样本中每个类别出现的概率以及在不同的类别下各个特征属性对应的条件概率估计,并根据记录下的计算结果生成和输出分类器。程序可根据上述讨论的公式对类别概率和条件概率完成自动计算。
构建训练集:

1)首先,计算公式(7)中的p(y=ck|x):
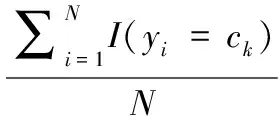
(8)
其中:I(x)为指示函数,若括号内成立,则计1,否则为0。
2)随后计算分子中的条件概率,设M维特征的第j维有L个取值,则在给定分类ck下某维特征的某个取值ajl的条件概率为:
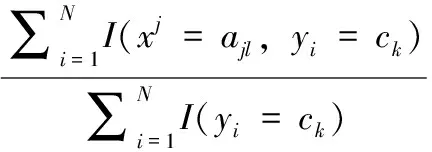
(9)
经过以上步骤便完成了学习的任务,也得到了诊断模型的基本概率。
2.3 分类
根据训练得到的诊断模型,就可以通过上述概率公式(9)进行计算未分类实例X属于各类的后验概率p(y=ck|X),在公式(7)中对所有的类别来说,其分母的值都相等,故只需计算分子部分即可,具体计算步骤如下:
1)计算该实例属于y=ck类的概率:

(10)
2)确定该实例所属的分类y:
y=argmaxp(y=ck|X)
(11)
3 慢性病诊断模型及实现过程
基于蜂群算法(ABC)和朴素贝叶斯的慢性病推理预测的ABC-NB整体模型如图2所示。
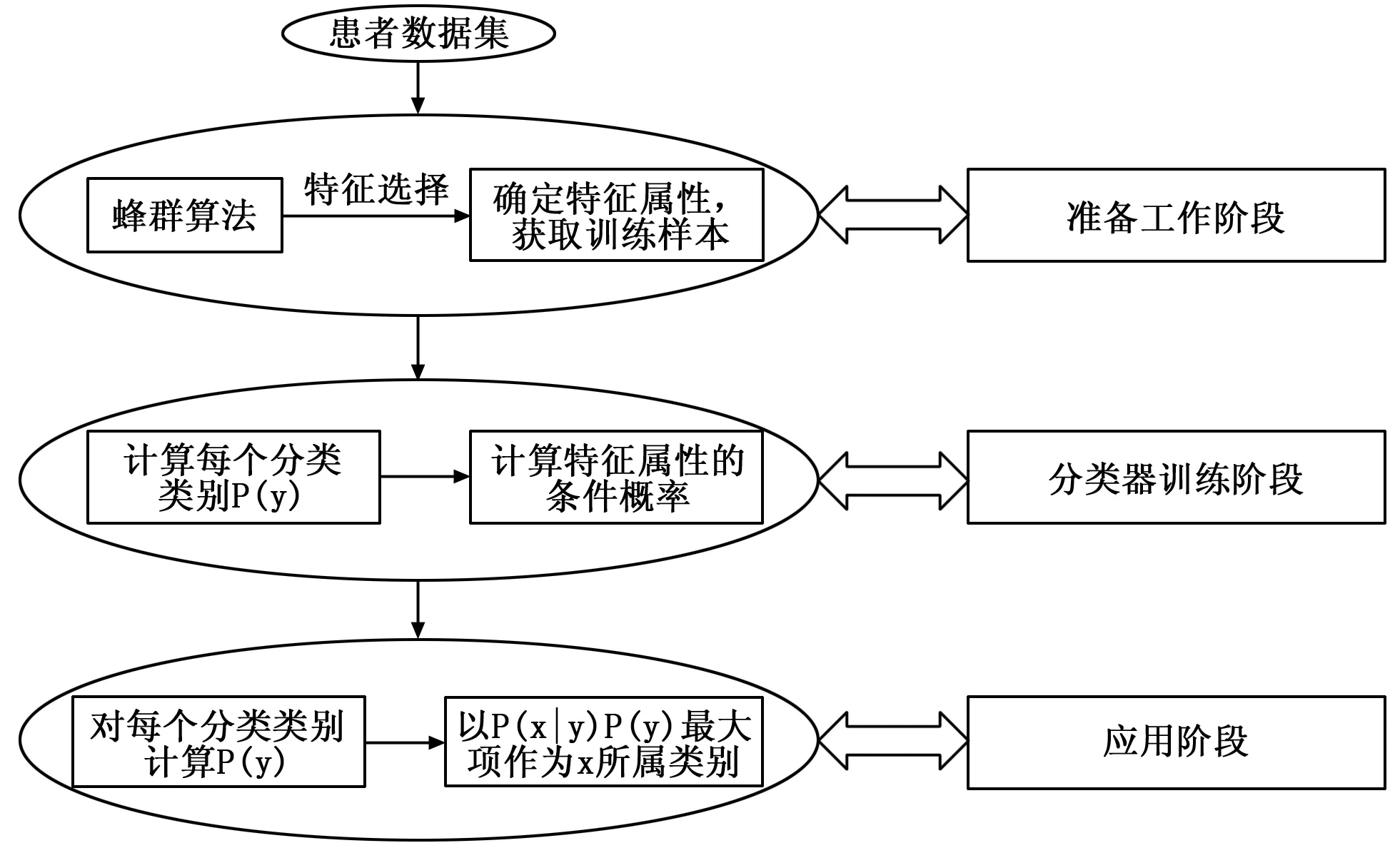
图2 ABC-NB整体模型图
本文选取了杭州某医院高血压患者的检验数据作为数据集,首先为朴素贝叶斯分类做准备,根据具体情况确定特征属性,输入是所有待分类样本数据,输出与分类器质量相关的特征属性和训练样本。根据公式(1)随机初始化一个蜜源,蜜群中每一个蜜源代表了一个特征子集,对特征子集进行特征选择。
蜂群算法特征选择的伪码如下:
Initialize the population of food sources N;
Evaluate the fitness;
Repeat(terminate criterion not satisfied)
Generate new food source using the equation:
wid=xid+φ(xid+xkd);
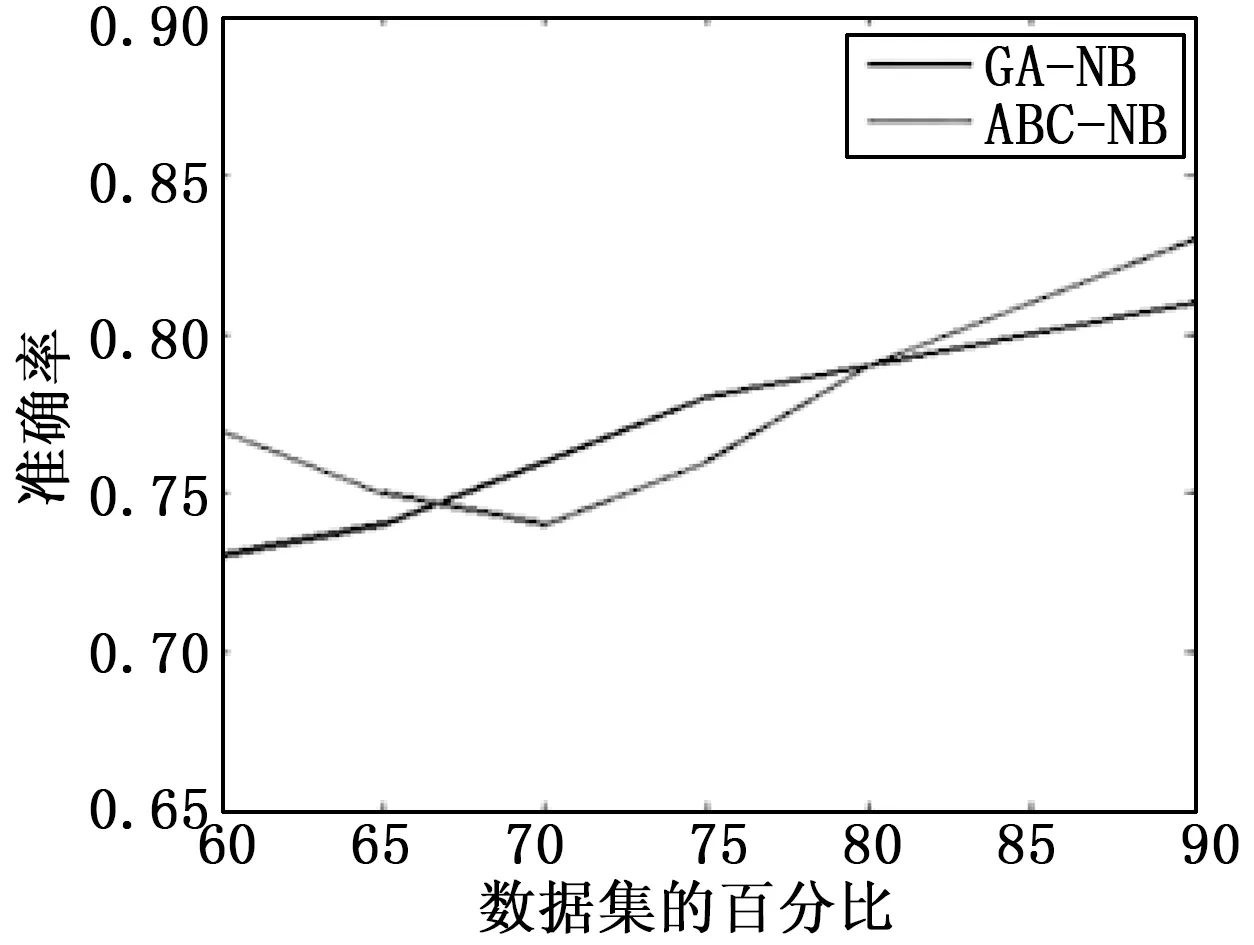
IFfit(wid) ELSE generate new food sources using the equation IF d>limit then ELSE d End 每进行一次迭代,根据公式(4)、(5)判断算法是否满足最优解的条件,如果满足,则输出最优解;反之则进入公式(2)继续进行迭代,在此我们通过公式(12)引进尺度调节因子改进公式(2)寻找蜜源,使之更加接近蜜源自然的寻蜜过程。 φi+1=φ,otherwise (12) 对于人工蜂群算法求最优解的终止条件,本文通过设定全局最大迭代次数和阈值为limit的局部最大迭代次数,用以保证算法终止。迭代完毕之后,输出最优解的蜜源,该蜜源所代表的特征子集即为最优特征子集。输出的该特征子集包含15个特征属性,分别为年龄、体质指数、胸围、腰臀比、总胆固醇、有无甲状腺功能亢进性突眼征或下肢水肿、血钾、血脂、高密度脂蛋白胆固醇、尿酸、性别、尿糖、胸主动脉、腹部动脉和股动脉有无杂音、高血压家族史、有无神经纤维瘤性皮肤斑。 在机器训练和学习的过程中会遇到从样本中算出的概率值为0的情况,这时需要引入拉普拉斯平滑方法,给学习步骤中两个概率计算公式(8) 、(9)的分子和分母都分别加上一个常数。更新过后的公式如下: (13) 其中:K是类的个数,该模型中类的个数为2,患病和不患病。 引入维度之后公式如下: (14) Lj是第j维特征的最大取值,平滑因子λ=0为公式(8)、(9)实现的最大似然估计,这时会出现刚刚提到的概率值为0的问题,而λ=1则避免了概率为0问题。引入平滑因子解决0概率之后,根据上述蜂群算法得出的最优特征子集,将包含特征属性的训练样本数据集进行朴素贝叶斯分类器训练,按照改进后的公式(14)机器计算出某维下各个特征的取值ajl在给定某分类ck下的条件概率,其中以年龄对慢性病患病的影响最大,作用效应为23.62%。 根据训练得到的条件概率,从15个特征属性中选择了8个作为最为最优的特征属性。分别为Age、Sex、BMI、URA、WHR、TC、BF、FHBP。因此朴素贝叶斯网络的特征属性就由这8个因素组成,类变量则为患病和不患病。根据上述选出的8个特征属性构建诊断模型的朴素贝叶斯结构如图3所示。 图3 慢性病诊断模型的朴素贝叶斯结构图 完成训练以及确定诊断模型的NB图后,根据上述的8个特征属性的值通过分类公式(10)进行机器计算和的概率,按照公式(11)选出最大的概率值,确定该样本所属的分类是患病还是不患病。 选取1 000个样本数据做为测试,其中700个样本为换高血压类别,300个位非高血压类别。作为参照试验,采用GA-NB算法同样对测试样本进行分类,评价标准如下所示: (15) 其中Y和N分别为患高血压和不换高血压数量,YR和YF为在患病样本中分类为患病和不患病的数量,NR和NF为在不患病的样本中分类为不患病和患病的数量。 样本的待分类项:E={e1,e2,…,e8},e1,e2,…,e8分别为E的一个特征属性,代表相关的高血压影响因子。 类别集合:C={yes,no},yes,no代表患病和不患病类别。进行机器计算类别概率分别为: p(y=yes)=p(E1|yes)p(E2|yes)…p(E8|yes)p(E) (16) p(y=no)=p(E1|no)p(E2|no)…p(E8|no)p(E) (17) 将实验样本数据分别按照本文模型以及GA-NB参照模型进行分类,实验结果如图4所示。 图4 GA-NB与ABC-NB的准确率对比 试验结果表明,随着数据集百分比的增加,GA算法更容易产生早熟收敛的问题,而ABC算法在迭代的过程中不断的更新尺度调节因子,使得在空间搜索蜜源的过程更接近蜂群在自然界采蜜的行为,可以引导蜂群按照更好的方向收敛到最优解,降低了特征子集的维度,从而优化了在分类训练阶段输入的特征属性,提高了模型分类的准确率。 随着当今互联网的快速发展,医疗领域产生了海量的临床数据,虽然医生可以直观的去查看和分析每一条临床数据进行诊断,但是一方面由于数据量巨大,超出了时间和精力所能接受的范围,只能看其中的一部分;另一方面医生根据临床经验和专业知识可能会造成诊断的不准确[10-11]。本文在分析蜂群算法原理和朴素贝叶斯分类器的基础上,提出了基于改进尺度因子的蜂群算法与朴素贝叶斯分类器结合的慢性病诊断模型,具有很好的柔性和鲁棒性,而且提高了模型的分类性能,减少了训练时间。医生可以根据模型分类的结果,将其和自己的临床经验以及专业知识相结合,这样不仅节省了时间,也能够提高诊断的准确率。再后续的研究中,将会在继续提高诊断分类准确率的同时研究将模型应用于不同的疾病领域。 [1] 王临虹. 慢性病防控要高度重视导致慢性病的社会决定因素[J]. 中国健康教育, 2013,29(5):388-389. [2] 许 腾. 基于甲状腺疾病的临床数据挖掘与分析研究[D]. 上海:东华大学, 2016. [3] 计智伟, 胡 珉, 尹建新. 特征选择算法综述[J]. 电子设计工程, 2011, 19(9):46-51. [4] Suguna N, Thanushkodi K. A Novel Rough Set Reduct Algorithm for Medical Domain Based on Bee Colony Optimization[J]. Computer Science, 2010. [5] 徐 晨, 曹 莉, 梁小晓,等. 基于ABC—BP神经网络的用电量预测研究[J]. 计算机测量与控制, 2014, 22(3):912-914. [6] Uzer M S, Yilmaz N, Inan O. Feature selection method based on artificial bee colony algorithm and support vector machines for medical datasets classification[J]. Scientific World Journal, 2013, 2013(11):419187. [7] Karaboga D, Basturk B. A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm[M]. Kluwer Academic Publishers, 2007. [8] Rish I. An empirical study of the naive Bayes classifier[J]. Journal of Universal Computer Science, 2001, 1(2):127. [9] 胡彩平, 倪志伟, 卢亦娟. Naive—Bayes模型及其在范例推理中的应用[J]. 计算机技术与发展, 2003, 13(5):23-25. [10] 滕 琪, 樊小毛, 何晨光, 等. 医疗大数据特征挖掘及重大突发疾病早期预警[J]. 网络新媒体技术, 2014 (1): 50-54. [11] 窦 强, 刘鸿齐, 晋晓强,等. 基于全程管理的“互联网+”慢性病管理模式[J]. 中华医学图书情报杂志, 2016, 25(7):22-26. ResearchonDiagnosticClassificationofChronicDiseasesBasedonABC-NB Wang Shangzhe,Zhang Yunhua (Zhejiang Sci-Tech University,Hangzhou 245000,China) In the medical field, it is very important for doctors to make effective and correct decision-making. In order to improve the accuracy of doctors' diagnosis and avoid the misdiagnosis of doctors' intuition, subconscious and incomplete knowledge. ABC-NB algorithm is used in the field of chronic disease diagnosis to improve the diagnostic efficiency and reduce the chance of misjudgment. The artificial bee colony algorithm based on improved scale factor is applied to the selection of chronic disease characteristics, and the data are dimensioned, the redundant and irrelevant features are removed, the convergence speed is improved, and the algorithm is applied to search the global optimal solution. Then, the eigenvalues of the pre-processed data are trained and learned to generate the Bayesian classifier to construct the prediction model. The prediction module displays the diagnostic results for medical staff to assist in the diagnosis and decision making. Experiments show that the model has good flexibility and robustness, can have a stable calculation of the probability of diagnosis of chronic diseases,and it is effective for the diagnosis of medical staff. diagnosis of chronic diseases;feature selection;ABC;naive Bayesian classifier 2017-05-02; 2017-05-26。 王尚哲(1991-),男,河南周口人,硕士研究生,主要从事智能信息处理方向的研究。 1671-4598(2017)11-0197-04 10.16526/j.cnki.11-4762/tp.2017.11.050 TP181 A
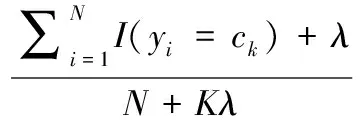


4 模型的实例计算
4.1 计算过程
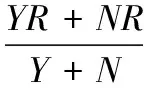
4.2 结果与分析
5 结束语
