轻型操作臂结合部弹性约束动力学特性及实验研究

刘玉飞 张 席 李 威 许德章

1.安徽工程大学机械与汽车工程学院，芜湖，2410002.安徽工程大学工程研发与训练中心，芜湖，2410003.中国矿业大学机电工程学院，徐州，221116

轻型操作臂结合部弹性约束动力学特性及实验研究

刘玉飞1,3张 席2,3李 威3许德章1

1.安徽工程大学机械与汽车工程学院，芜湖，2410002.安徽工程大学工程研发与训练中心，芜湖，2410003.中国矿业大学机电工程学院，徐州，221116

对结合部弹性约束下轻型操作臂系统的动力学特性进行了研究。首先，基于结合部的线约束刚度，建立了轻型操作臂的弹性约束模型，得到系统的频率特性方程；其次，基于建立的弹性约束模型，采用哈密顿变分原理推导了系统的振动位移方程；最后，采用理论仿真和实验方法对轻型操作臂弹性约束系统的动力学特性进行分析，探讨了结合部弹性约束对系统动态特性的影响机理。研究结果表明：所建弹性约束模型能够表征结合部的弹性约束作用，尤其对高阶模态的分析具有较高精度；在弹性约束区域内，频率与约束刚度之间具有幂函数关系特征，前两阶频率拟合误差分别小于0.08%和0.45%；振动位移分析误差为2.38%，通过实验验证了系统弹性约束模型和动力学分析结果的正确性。

轻型操作臂；结合部；弹性约束；动力学

0 引言

操作臂是机器人的重要组成部分，通过操作机构及其末端执行器完成特定的操作任务，在机械加工、精密装配以及上下料、喷涂等作业中有着广泛应用[1-3]。现代制造装备正不断向轻型和集成化方向发展，传统的刚性操作臂已难以满足该发展要求[4]。轻型操作臂与传统的刚性操作臂相比具有轻质、灵活以及执行高速大范围操作时能量消耗较低等特点[5-6]。在保证功能的同时，轻型操作臂可显著减小结构的质量，并且是典型的柔性结构，有利于实现结构的智能控制[7]。由于采用轻质材料，轻型操作臂的刚度和阻尼均较小，在执行操作、启停以及运动转换的过程中极易受到外界激励而产生弹性振动，并非完全的刚性结构特性，且在高速操作时振动更为明显[5, 8-9]。弹性振动严重影响了操作臂的操作性能和控制精度，降低了结构寿命，因此需要对轻型操作臂的动态特性进行研究。

轻型操作臂的操作机构通过结合部与机器人本体连接组成耦合系统[10]，结构间的耦合作用进一步影响系统的动态特性，而这种耦合作用是通过结合部传递的，因此在分析轻型操作臂的动力学特性时有必要考虑结合部性能的影响。本文考虑结合部的弹性约束效应，通过仿真分析和实验对结合部弹性约束下的轻型操作臂弹性约束系统的动力学特性进行研究。

1 轻型操作臂弹性约束系统动力学方程

1.1 弹性约束系统频率方程

分析轻型操作臂的动力学特性，首先要根据结合部的约束性能建立系统的约束模型。在理想情况下，操作机构与机器人本体之间结合部的约束被视为完全刚性的，而在实际过程中由于预紧力控制不准以及服役过程产生松动的影响，结合部常表现出一定的弹性约束效应，影响系统的整体性能。由文献[11]可知，结合部的弹性约束效应可以用线约束和扭转约束的叠加表示。此外，根据模态灵敏度分析结果，线约束对系统的影响占主要成分[12]。为此，本文考虑结合部的线约束作用对其弹性约束效应进行表征。通过系统子结构划分，将系统划分为操作机构、机器人本体和结合部子结构，并建立系统的弹性约束模型如图1所示。其中，k为约束刚度，c为阻尼系数。

图1 轻型操作臂系统子结构划分及弹性约束模型Fig.1 Substructure division and elastic restraint model of the flexible manipulator system

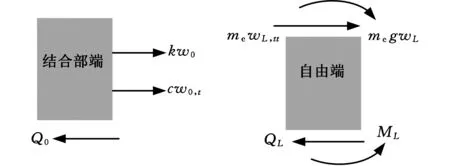
图2 轻型操作臂弹性约束系统的受力分析Fig.2 Force analysis of the elastic restraint joints for the flexible manipulator

根据材料力学理论[13]，轻型操作臂弹性形变产生的剪力Q和弯矩M分别为

(1)

I=bh3/12

式中，E为弹性模量；I为惯性矩；b为宽度；h为厚度。

根据结合部端的力平衡关系可得

(2)

(3)

同理可得自由端(x=L)的边界条件如下：

(4)

由式(3)可以看出，当轻型操作臂的结合部端存在相对速度时，结合部阻尼对系统的边界条件会产生一定的影响。而在实际操作过程中操作机构与机器人本体之间相对速度较小，且结构阻尼对系统模态特性影响较小[14]，因此，在分析轻型操作臂弹性约束系统的模态特性时，忽略结合部阻尼的影响。

根据模态叠加原理[14]，轻型操作臂的振动位移w(x,t)可表示为

(5)

式中，q(t)为系统的广义坐标；φ(x)为轻型操作臂的振型函数。

为此，结合部弹性约束下轻型操作臂的边界条件可简化为

(6)

(7)

式中，ω为轻型操作臂的角频率。

不失一般性，将结合部弹性约束下轻型操作臂的振型函数表示为[14]

φ(x)=α1sinβx+α2cosβx+α3sinhβx+α4coshβx

(8)

(9)

A=bh

式中，α1、α2、α3、α4均为由边界条件确定的系数;β为与角频率ω有关的量;ρ为质量密度；A为横截面面积。

将式(8)分别代入式(6)和式(7)并将结果写成矩阵形式：

(10)

λ=EIβ2

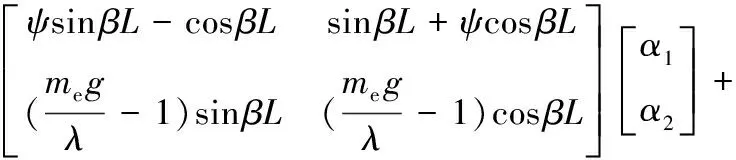
(11)

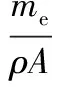
根据式(10)和式(11)，消去系数α3、α4，得

(12)

Δ21=βψ(sinhβL-sinβL)+β(cosβL+coshβL)

Δ22=βψ(coshβL-cosβL)-β(sinβL-sinhβL)

为保证振型函数的存在，式(8)的系数α1、α2、α3、α4不全为零。则式(12)需满足

(13)

将式(13)展开可得结合部弹性约束下轻型操作臂的模态频率方程如下：

(14)

从式(14)可以看出，轻型操作臂的模态频率与结合部约束刚度密切相关，当忽略末端执行器负载的作用(即me=0)时，轻型操作臂弹性约束系统的频率方程可转化为

βλcosβLsinhβL+βλsinβLcoshβL-
kcosβLcoshβL-k=0

(15)

通常意义下假设的结合部完全刚性约束所对应的约束条件为k→+∞，代入式(15)得

cosβLcoshβL+1=0

(16)

式(16)即为理想固定约束下轻型操作臂的频率方程。由此说明，将结合部视为完全刚性只是一种理想情况，若忽略结合部的弹性约束作用而将其视为理想的固定约束，将导致分析结果出现误差甚至错误，尤其对操作精度有一定要求的轻型操作臂具有重要的影响。另外，以上求解过程验证了所得频率方程的正确性，同时也说明本文所建弹性约束模型能够合理表征结合部的弹性约束作用，且与文献[11]采用线约束和扭转约束组合建模相比，本文所建弹性约束模型更为简化。

1.2 弹性约束系统振动位移方程

在轻型操作臂执行操作任务的过程中存在弹性振动，弹性振动对系统动态性能具有明显影响。为此，以轻型操作臂平移运动为例，建立轻型操作臂弹性约束系统的动力学方程，并对系统的振动特性进行分析。

系统的动能ET为

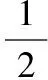
(17)

系统的势能主要考虑轻型操作臂的弹性势能：

(18)

式中，EV为系统的势能；Ki为系统的模态刚度。

定义拉格朗日函数U为

U=ET-EV

(19)

根据哈密顿变分原理[13]，式(19)满足

(20)

(21)

(22)

将式(21)和式(22)代入式(20)，可得轻型操作臂广义坐标运动方程如下：

(23)

根据杜哈梅积分[14]，轻型操作臂的振动位移方程为

(24)

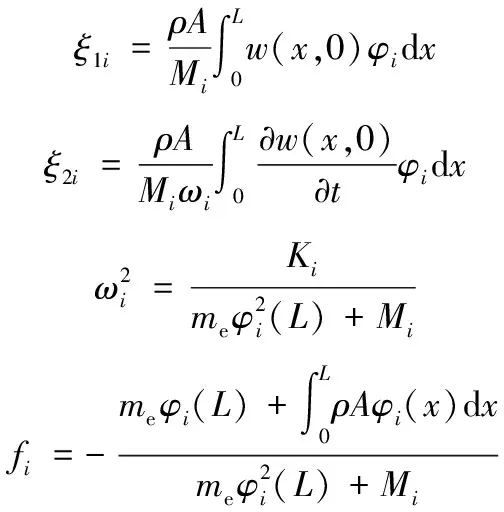
结合式(18)，可得轻型操作臂的横向振动位移如下：

(25)

φ(x)即为结合部弹性约束下轻型操作臂的振型函数，可以看出，轻型操作臂的振动特性与结合部约束密切相关，由式(8)和式(10)可得

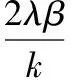
(26)

2 仿真与实验分析

2.1 频率特性分析及特征拟合

式(15)给出了结合部弹性约束下轻型操作臂弹性约束系统的频率方程，基于此对轻型操作臂弹性约束系统的频率特性作进一步分析。本文主要分析轻型操作臂的前三阶模态频率，并采用数值方法对频率方程进行求解。选取的轻型操作臂的结构参数如表1所示。

表1 轻型操作臂的结构参数Tab.1 Structural parameters of the flexible manipulator

图3所示为结合部约束刚度k对轻型操作臂模态频率的影响。由图3可以看出，随着约束刚度的增大，前三阶频率均增大,并逐渐趋于理想的固定约束情形下的前三阶频率(10.6801 Hz、66.9317 Hz、187.4121 Hz)，结合部弹性约束下前三阶频率小于理想固定约束情形。可将区间[1.0×104N/m、1.0×106N/m视为结合部的弹性约束区域，在该区域内模态频率与约束刚度之间的关系曲线具有幂函数的特性。为进一步确定约束刚度与模态频率之间的关系，采用幂函数对该区间的频率曲线进行拟合。因此，构造近似函数为

(a)第一阶 (b)第二阶 (c)第三阶图3 约束刚度k与模态频率的关系Fig.3 Relationship between the tensional restraint stiffness k and the mode frequencies

(27)

式中，ωni为模态频率；ai、bi、ci为待定系数。

基于MATLAB曲线拟合工具箱cftool，得到轻型操作臂前三阶频率拟合曲线,分别如图4、图5和图6所示，各阶频率拟合方程系数的可信取值范围如表2所示。

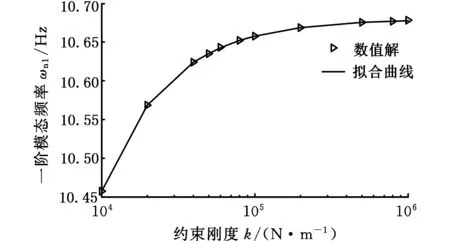
图4 一阶模态频率拟合曲线Fig.4 Fitting curve of the first order mode frequency

图5 二阶模态频率拟合曲线Fig.5 Fitting curve of the second order mode frequency

图7所示为根据频率拟合方程求解得到的频率值的误差。由图7可以看出，一阶频率和二阶频率拟合误差分别小于0.08%和0.45%，当约束刚度较低时，三阶频率的拟合误差大于一阶和二阶，但随着约束刚度的增大，各阶频率的拟合误差均明显减小。由此说明，构造的频率拟合方程可表征结合部弹性约束与频率的关系，且对前两阶模态具有较高精度。

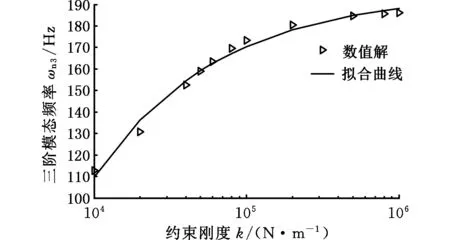
图6 三阶模态频率拟合曲线Fig.6 Fitting curve of the third order mode frequency

表2 频率拟合方程系数的可信取值范围Tab.2 Reliable values of the frequency fitting equation coefficients

2.2 实验测试与分析

为了对本文轻型操作臂弹性约束系统理论分析的结果作进一步分析和验证，故搭建轻型操作臂实验平台，进行模态和动力学测试实验，如图8所示。轻型操作臂操作机构采用环氧树脂板进行模拟，与机器人本体之间采用螺栓连接以模拟结合部的作用。实验采用力锤激励、单点拾振法。建立模态分析模型时，将操作臂长度等分为10段，宽度等分为2段，厚度视为1段，并根据节点确定测点布置，如图9所示。选取测点3为拾振点，其余点为激励点。操作臂测点3的位置固定压电式加速度传感器，型号为DH131，用来采集操作臂的振动信号，同时模拟负载作用；电荷适调器型号为DH5857-1，用来采集信号的转化、处理和放大；模态分析软件选用DH5927N动态信号采集分析系统。

(a)第一阶 (b)第二阶 (c)第三阶图7 频率拟合结果误差Fig.7 Error analysis of the frequencies fitting

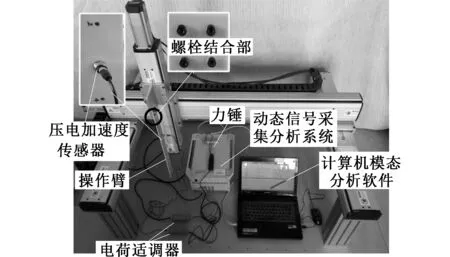
图8 轻型操作臂模态测试实验系统Fig.8 Experiment system for the modal test of the flexible manipulator

图9 测点布置图Fig.9 Distribution of the measuring points

采用力锤激励，通过动态信号采集分析系统实时采集激励力和响应振动信号，得到10组频响函数数据。将测试得到的数据添加到模型数据中，选用多参考点最小二乘复频域法(PolyLSCF法)对频响函数数据进行分析，计算得到轻型操作臂的前三阶频率分别为9.12 Hz、55.59 Hz、151.85 Hz。图10所示为模态分析模型验证，可知模态实验结果是正确的。

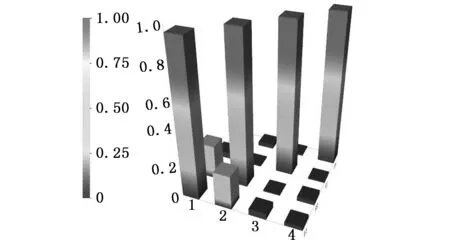
ωn1=9.12 Hz ωn2=55.59 Hz ωn3=151.85 Hz ωn4=310.31 Hz图10 模态分析模型验证Fig.10 Model verification for modal analysis

根据图7所示的频率拟合误差可以看出，频率拟合曲线对一阶模态具有较高的精度，根据实验得到的一阶频率，选取弹性约束刚度k=1.0×104N/m进行分析。代入式(27)计算得轻型操作臂的前三阶频率分别为10.4498 Hz、51.0843 Hz、146.0061 Hz。图11所示为轻型操作臂模态频率误差,图中的百分数为不同约束模型所对应的频率分析误差。由图11可以看出，根据结合部弹性约束模型得到的前三阶频率与实验结果较为吻合，弹性约束模型误差明显小于理想固定约束假设模型。且随着频率阶数的增大，理想固定约束模型的误差逐渐增大，而弹性约束模型误差逐渐减小，即对高阶模态而言，弹性约束模型分析精度更高，验证了本文建立的结合部弹性约束模型的正确性和合理性。

图11 轻型操作臂模态频率分析误差Fig.11 Frequencies error analysis for the flexible manipulator

为进一步分析结合部弹性约束下轻型操作臂的动态特性，基于模态测试实验装置进行振动测试实验。实验时采用力锤对测点5进行激励，同时采集力锤的激励信号和测点3(拾振点)的振动信号，可得轻型操作臂的初始振动加速度幅值为98.66 m/s2，实验过程中在阻尼作用下逐步衰减，如图12所示。由式(25)所得的振动位移方程计算可知，在激励作用下轻型操作臂的振动加速度幅值为96.31 m/s2，如图13所示。与实验结果误差为2.38%，说明基于弹性约束模型分析轻型操作臂弹性约束系统的动态特性是可行的。

3 结论

(1)结合部的弹性约束效应对轻型操作臂的动力学特性具有重要影响，若将其视为理想的刚性约束，将导致分析结果存在误差甚至错误，在分析系统的动力学特性时应充分考虑结合部的弹性约束作用。

(2)建立的弹性约束模型能够合理表征结合部的弹性约束作用，尤其对高阶模态的分析精度较高，实验结果验证了弹性约束模型的正确性。

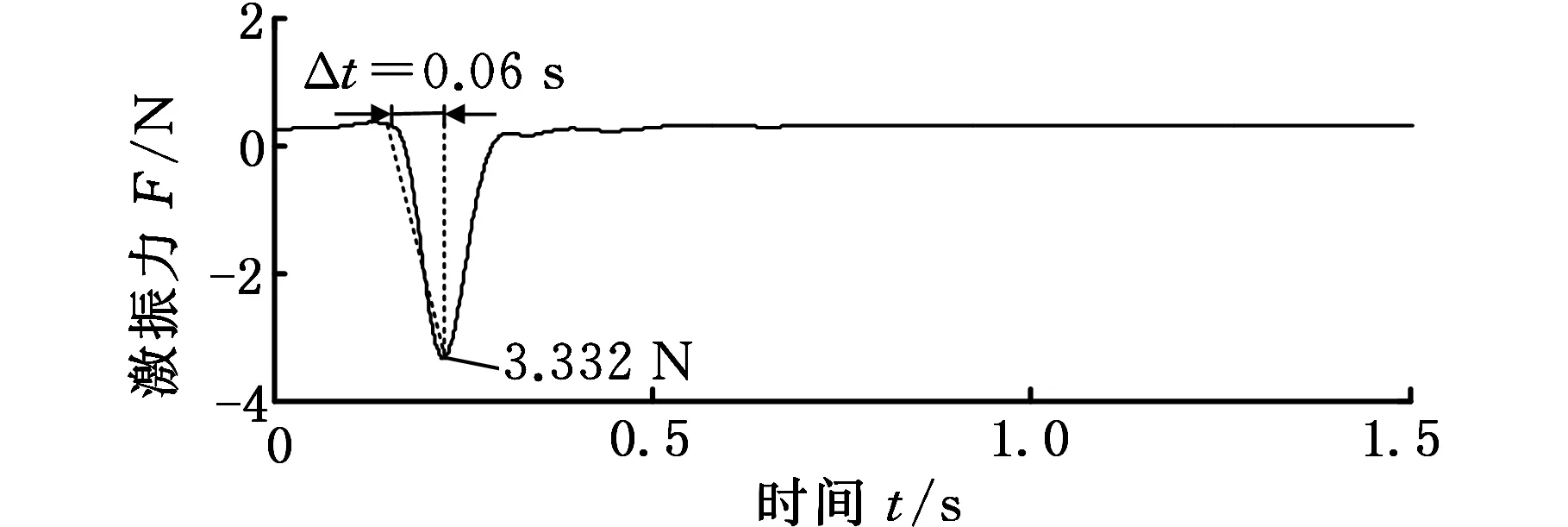
(a)激励信号

(b)振动加速度图12 力锤激励信号和振动加速度响应Fig.12 Force hammer excitation signal and vibration acceleration response

图13 轻型操作臂的振动加速度理论结果Fig.13 The theoretical results of vibration acceleration of the flexible manipulator

(3)轻型操作臂的频率与结合部的约束刚度具有一定关系，在弹性约束区域内，频率与约束刚度之间具有幂函数关系特征，并通过曲线拟合可得到频率与结合部约束刚度的关系方程，所得拟合方程对前两阶模态的分析结果误差分别小于0.08%和0.45%。

(4)研究了结合部弹性约束效应对轻型操作臂系统的动态特性的影响规律，所得结果可指导轻型操作臂的关节特征识别、设计优化和振动抑制，这将是后续深入研究的内容。同时，本文重点是分析轻型操作臂弹性约束系统的动力学特性，没有考虑系统阻尼因素，在后续研究中也将考虑系统阻尼尤其是结构阻尼对系统特性的影响。

[1] 金鹏，刘建新，史素敏.抛光直角坐标机器人控制系统设计[J].机械设计与制造，2013(9)：200-202.

JIN Peng, LIU Jianxin, SHI Sumin.Design of Control System for Polishing Cartesian Coordinate Robot [J]. Machinery Design and Manufacture,2013(9):200-202.

[2] 赵言正，付庄，曹其新，等.空间太阳电池封装机器人[J].上海交通大学学报，2005，39(6)：888-891.

ZHAO Yanzheng, FU Zhuang, CAO Qixin, et al. A Space Solar Cell Bonding Robot [J]. Journal of Shanghai Jiaotong University,2005,39(6):888-891.

[3] 王田苗，陶永.我国工业机器人技术现状与产业化发展战略[J].机械工程学报，2014，50(9)：1-13.

WANG Tianmiao, TAO Yong. Research Status and Industrialization Development Strategy of Chinese Industrial Robot [J]. Journal of Mechanical Engineering,2014,50(9):1-13.

[4] 雷源忠. 我国机械工程研究进展与展望[J].机械工程学报，2009，45(5)：1-11.

LEI Yuanzhong. Recent Research Advances and Expectation of Mechanical Engineering Science in China [J]. Journal of Mechanical Engineering,2009,45(5):1-11.

[5] DWIVEDY S K, EBERHARD P. Dynamic Analysis of Flexible Manipulators, a Literature Review [J].Mechanism and Machine Theory,2006,41(7):749-777.

[6] RAHIMI H N, NAZEMIZADEH M. Dynamic Analysis and Intelligent Control Techniques for Flexible Manipulators: a Review [J].Advanced Robotics,2014,28(2):63-76.

[7] HURLEBAUS S, GAUL L. Smart Structure Dynamics [J].Mechanical Systems and Signal Processing,2006,20:255-281.

[8] ZHAO J L, YAN S Z, WU J N. Analysis of Parameter Sensitivity of Space Manipulator with Harmonic Drive Based on the Revised Response Surface Method[J]. Acta Astronautica,2014,98:86-96.

[9] MAHMOODI S, AHMADIAN M. Modified Acceleration Feed-back for Active Vibration Control of Aerospace Structures [J]. Smart Materials & Structures,2010,19(6):065015.

[10] WANG F Y, GAO Y Q. Advanced Studies of Flexible Robotic Manipulators: Modeling, Design, Control, and Applications [M]. Singapore: World Scientific,2004.

[11] 刘玉飞，李威，杨雪锋，等.弹性关节柔性操作臂的频率及振型特性分析[J].中国机械工程，2015，26(7)：954-959.

LIU Yufei, LI Wei, YANG Xuefeng, et al. Natural Frequencies and Modal Shape Characteristics of a Flexible Manipulator with Elastic Joints[J].China Mechanical Engineering，2015，26(7)：954-959.

[12] LIU Yufei, LI Wei, WANG Yuqiao, et al. Dynamic Model and Vibration Power Flow of a Rigid-flexible Coupling and Harmonic-disturbance Exciting System for Flexible Robotic Manipulator with Elastic Joints[J].Shock and Vibration,2015,2015:1-10.

[13] 梅凤翔.分析力学[M].北京：北京理工大学出版社，2013.

MENG Fengxiang. Analytical Mechanics[M]. Beijing: Beijing Institute of Technology Press,2013.

[14] SINGIRESU S R. Mechanical Vibration, 5th edition [M]. New York: Pearson Education Inc.,2011.

DynamicsPropertiesandExperimentalInvestigationsforLightManipulatorswithElasticRestraintJoints

LIU Yufei1,3ZHANG Xi2,3LI Wei3XU Dezhang1

1.School of Mechanical and Automotive Engineering, Anhui Polytechnic University, Wuhu,Anhui,241000 2.Engineering Research and Training Center, Anhui Polytechnic University, Wuhu,Anhui,241000 3.School of Mechatronic Engineering, China University of Mining and Technology, Xuzhou,Jiangsu,221116

The dynamics properties of flexible manipulator systems with elastic restraint joints were investigated. Firstly, an elastic restraint model with the linear restraints was established, and then, the frequency equation was subsequently derived. Secondly, based on the established elastic restraint model and Hamilton principle, the vibration displacement equation was derived. Finally, the dynamics properties of the flexible manipulator elastic restraint systems were analyzed using theoretical simulation and experimental approach, and the influence mechanism of elastic restraints on the dynamics were revealed. The results show that the established model may describe the elastic restraints of joints, particularly for higher order modes. Moreover, in the defined elastic restraint regions, the relationship of the frequency and the restraint stiffness has the characteristics of power function, and the fitting errors for the first two order frequencies are small than 0.08% and 0.45%, respectively, and the analysis errors for the vibration displacements are as 2.38%, which were verified experimentally.

light manipulator; joint; elastic restraint; dynamics

TH112;TH113.1

10.3969/j.issn.1004-132X.2017.23.004

2017-01-09

国家自然科学基金资助项目(51305444)；安徽高校自然科学研究项目(KJ2017A118)；安徽省科技攻关计划资助项目(1604a0902125、1604a0902183)；芜湖市科技计划资助项目(2016cxy03)；安徽工程大学大学引进人才科研启动基金资助项目(2016YQQ012)

(编辑胡佳慧)

刘玉飞，男，1988年生。安徽工程大学机械与汽车工程学院讲师,中国矿业大学机电工程学院博士。主要研究方向为机器人系统动力学与控制。发表论文10余篇。E-mail：liuyufeiahpu@126.com。张席，女，1991年生。安徽工程大学工程研发与训练中心讲师，中国矿业大学机电工程学院硕士。李威，男，1964年生。中国矿业大学机电工程学院教授、博士研究生导师。许德章，男，1964年生。安徽工程大学机械与汽车工程学院教授。