管道内压力对纵模导波传播特性的影响

蔡海潮 徐春广 王东峰 尚振东

1.河南科技大学机械装备先进制造河南省协同创新中心，洛阳,4710032.北京理工大学机械与车辆学院，北京,1000813.洛阳轴研科技股份有限公司，洛阳,471039

管道内压力对纵模导波传播特性的影响

蔡海潮1徐春广2王东峰3尚振东1

1.河南科技大学机械装备先进制造河南省协同创新中心，洛阳,4710032.北京理工大学机械与车辆学院，北京,1000813.洛阳轴研科技股份有限公司，洛阳,471039

工程应用中的管道内部往往存在一定的介质，这些介质会对管内壁产生一定的压力，研究超声导波技术对管道进行检测时，介质产生的压力对超声导波传播特性的影响非常重要。采用数值模拟方法研究了管道内液体介质压力对超声导波传播的影响，分析了不同激励频率和不同介质压力时的导波衰减特性，并搭建了压力管道实验系统。实验结果表明，超声导波在管道内传播时传播速度不随管内压力的变化而变化。

管道；压力；纵模导波；传播特性

0 引言

在石油石化、核电等工业部门中，存在着大量的管道，这些管道为保障可靠有效的经济运行起到了重要作用。实践表明，管道在长期运行中，伴随着管道材料性质的变化，往往会出现诸如裂纹、腐蚀等缺陷，进而严重危及管道的安全运行，因此，对管道状况及时进行检测具有重大的现实意义。

超声导波检测技术是一种新型无损检测技术，近年来得到了人们的广泛关注，尤其是该技术在管道中的应用得到了深入研究，目前研究主要集中在超声导波技术对空管的检测能力上[1-4]。但对于工程中的管道，不仅有自由边界管道，而且还有很多非自由边界管道。非自由边界管道内部不仅充满了存在一定压力的液体或气体，而且外部往往也有包覆层或者被土壤层覆盖，这些物质的存在对超声导波的传播必然会产生较大的影响，大大限制了超声导波技术的检测能力，故有学者逐渐开始探讨管道内介质、管道外包覆层和土壤层等对超声导波传播特性的影响。文献[5-7]研究了充水管道中的导波传播特性以及与缺陷之间的相互作用；文献[8-11]研究了有包覆层存在时的导波传播特性；文献[12-13]研究了埋地管道中的导波传播特性；文献[14-15]研究了内载有水介质的地埋管道中的超声导波传播特性。然而管内介质产生的压力对超声导波传播特性影响的研究还较少，正是管道内存在压力才极易导致管道内应力集中部位或已出现缺陷部位引发重大安全事故。超声导波在金属管中的传播问题实际上是一个力学问题，因此应研究分析管内压力是否对超声导波传播产生了较大的影响。本文采用数值模拟和实验研究的手段研究管道内压力对超声导波传播的影响，揭示超声导波在非自由边界管道中的传播规律。

1 带流体负载管道中超声导波传播模型

图1为非自由边界管道示意图，管中介质为液体或气体。圆柱坐标系中的z轴为管道中心轴，管道的内外半径分别用b和a表示。

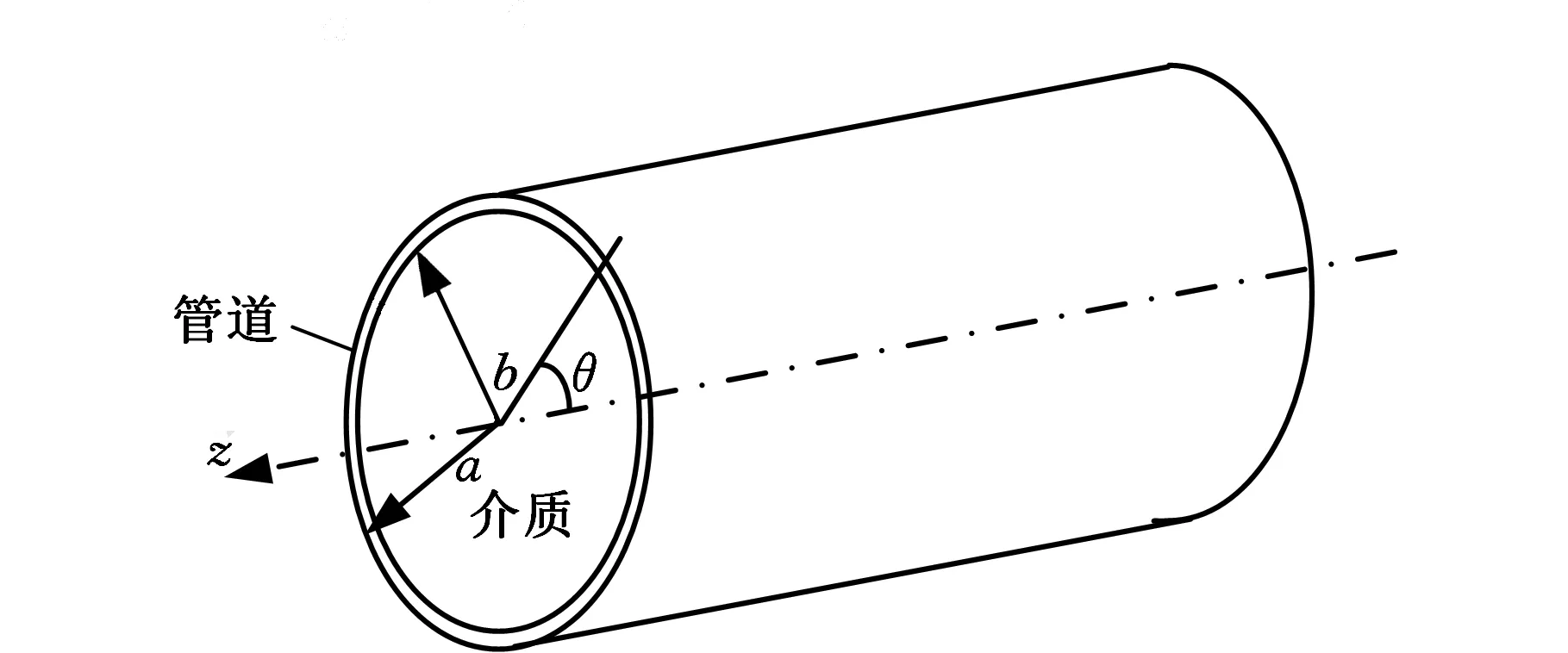
图1 非自由边界管道示意图Fig.1 Schematic of not free boundary pipe

由弹性力学可知，管道中的质点位移满足纳维(Navier)方程，假设管道中的液体为刚体，则液体圆柱体中传播的超声波也满足纳维方程[5]，将纳维方程进行斯托克斯-赫姆霍兹分解后，可分别求得固体管道中的位移us和液体中的位移uf。

为研究带液体负载管道的超声导波传播特性，需要同时考虑固体管道中导波的传播和液体之间的相互作用，建立充液管道的频散方程时要同时考虑管道内外表面的边界条件。对于充液管道，其外表面管径r=a满足的边界条件如下[16]：

(1)

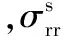
管内径r=b为管道内表面和液体的交界面，因此，管道内表面的径向位移是连续的，径向应力也是连续的且等于其作用于管内壁的压力，由于液体中不能产生剪切应力，故相应的应力分量为零，管壁内表面的边界条件如下：

(2)

将前面求得的固体位移us和液体位移uf以及应力代入式(1)和式(2)，得到一组特征方程[17]：

NY=0

(3)

Y=[AsA1A2BsB1B2Mf]T

式中,As、A1、A2、Bs、B1、B2、Mf均为求解波在非自由边界管道中传播的波动方程所获得的贝塞尔函数的系数,且这些系数均为常数。

为使式(3)存在非零解，其系数矩阵行列式应该为零，即

|N|=0

(4)

式(4)即为含液体介质管道中超声导波的频散方程。由于该方程是超越方程，无法得到解析解，因此采用数值法进行求解。数值求解频散方程过程分为寻根算法和跟踪算法两步。寻根算法首先固定频散方程中的一个变量，而使另一个变量以固定的增量在定义域内改变，求解函数的极小值作为函数根的近似解，并从该近似解出发，进一步细化得到每一种导波模态在容差范围内的精确解。然后将得到的每一个根(数值解)作为起始点，从已得到的数值解进行外推，从而得到新的近似解(估计变量)，再进一步采用精确寻根的方法求得精确解。这样不断研究路径上的每一点，依次迭代，直到研究范围的最大频率时终止，最终跟踪出的变量缓慢增加时的曲线即为频散曲线。

图2所示为采用数值求解法求得的充水管道超声导波纵向模态传播频散曲线。计算所用的管道外径为273 mm，壁厚为7 mm。管道材料为X70管道钢，其密度ρs=7850 kg/m3，纵波波速Cl为5900 m/s，横波波速Ct为3200 m/s。液体材料参数的密度ρf=1000 kg/m3，纵波波速Cf1为1500 m/s。

图2a、图2b分别为充液管道纵向模态的相速度和群速度频散曲线。沈立华等[18]绘制了自由边界管道的频散曲线，与自由边界管道频散曲线相比，充液管道频散曲线模态数量增加，出现一种新的纵向轴对称模态(α模态)，该模态高频时在管壁上主要做弯曲运动。相速度频散曲线与自由边界管道相比各模态相速度均减小，各模态截止频率也减小，且每个模态在低频处都存在几乎不发生频散的频段，在实际检测时可利用每个模态不发生频散的频段进行检测，来降低频散对导波信号分析处理的影响，故而选择模态L(0，2)不发生频散的频段对充液管道进行检测。

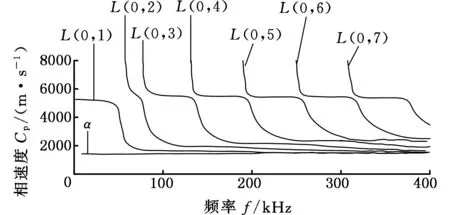
(a)相速度频散曲线

(b)群速度频散曲线图2 充液管纵向模态频散曲线Fig.2 Longitudinal modal dispersion curve of liquid pipe

2 带流体管道纵模导波传播的数值模拟

2.1 有限元模型建立

模拟研究带流体管道中导波传播特性时不仅需要考虑导波在管道中的传播问题，也需要考虑导波对内充介质的作用以及内充介质对导波传播的影响，求解耦合波动问题时采用数值模拟的方法进行。

对无缺陷带负载管道建立三维有限元(FEM)模型，管道外径为273 mm，壁厚为7 mm，在管道一端沿轴向加载激励频率为0.07 MHz的含5个波峰的窄带激励信号作为位移载荷来激励出纵向模态超声导波，在管道另一端提取轴向位移信号进行分析。

在边界条件设定时，假设管道内流体为不可压缩牛顿流体，根据雷诺数定义和管道中流体性质，流体流动选择层流模型。研究中不考虑热量的传递。

有限元模型中管道材料模型为X70管道钢，其弹性模量为206 GPa，泊松比为0.33，密度为7800 kg/m3。管内流体材料模型为水，其动力黏度为1.01×10-3Pa·s，密度为1000 kg/m3。

管道和流体的单元模型分别用固体力学模块和层流模块表示，在边界条件设定时，由于管壁为刚性条件，管道中传播的超声导波引起的位移非常小，因而管壁与流体之间的界面基本不发生相对滑动。在仿真模拟中假设管壁与流体之间无滑移、无渗透。流体的入口压力设定为1 MPa，出口压力设定为0，可以认为流体是充分发展流动的。

含流体管道网格的剖分选用自由剖分三角形单元，计算获得管道网格划分的最大网格步长为 9.5 mm[19]。为提高计算精度且保证计算速度，在仿真模拟中管道网格尺寸取单元格的最大尺寸9 mm。在流体网格划分时，为保证近管壁面有限元模拟计算的准确性，对近管壁面网格要进行适当加密。

研究中，综合考虑计算结果的精度以及计算机的运算能力,时间步长设定为0.5 μs。

2.2 数值模拟结果

为了研究不同管内压力对超声导波传播特性的影响，本文通过三维有限元模型对不同管内压力情况下的超声导波传播特性进行分析研究。分别选择5周期、中心频率为40 kHz、70 kHz、100 kHz、130 kHz、160 kHz作为激励信号对管内压力分别为0、2 MPa、4 MPa、6 MPa、8 MPa时的超声导波衰减特性进行研究。当管道一端受激励信号激励时，将会产生纵向模态超声导波并沿管道轴向传播。当导波传播至管道另一端时，由于端面的作用产生端面回波，然后反向传播至导波激励端，在传播过程中可能产生模态转换。计算完成后，提取从激励端传播至另一端的时间位移历程曲线，分别提取表面8个节点的位移信号后求取平均作为导波传播时间位移历程信号。图3为激励频率70 kHz、不同管内压力时导波传播有限元模拟结果的时间位移历程曲线。

由图3可以看出不同管内压力时间位移曲线中回波信号的峰值和传播时间，也可求出纵向模态L(0,2)的传播速度和随管内压力变化的幅值衰减情况。提取激励信号峰值与管内无压力回波峰值的时间为0.187 ms，经计算可得导波传播速度为5270 m/s，并采用同样方法计算管内压力分别为2 MPa、4 MPa、6 MPa、8 MPa时的导波传播速度均为5270 m/s。结果表明，导波传播速度不随管内压力的变化而变化。

(a)p=0

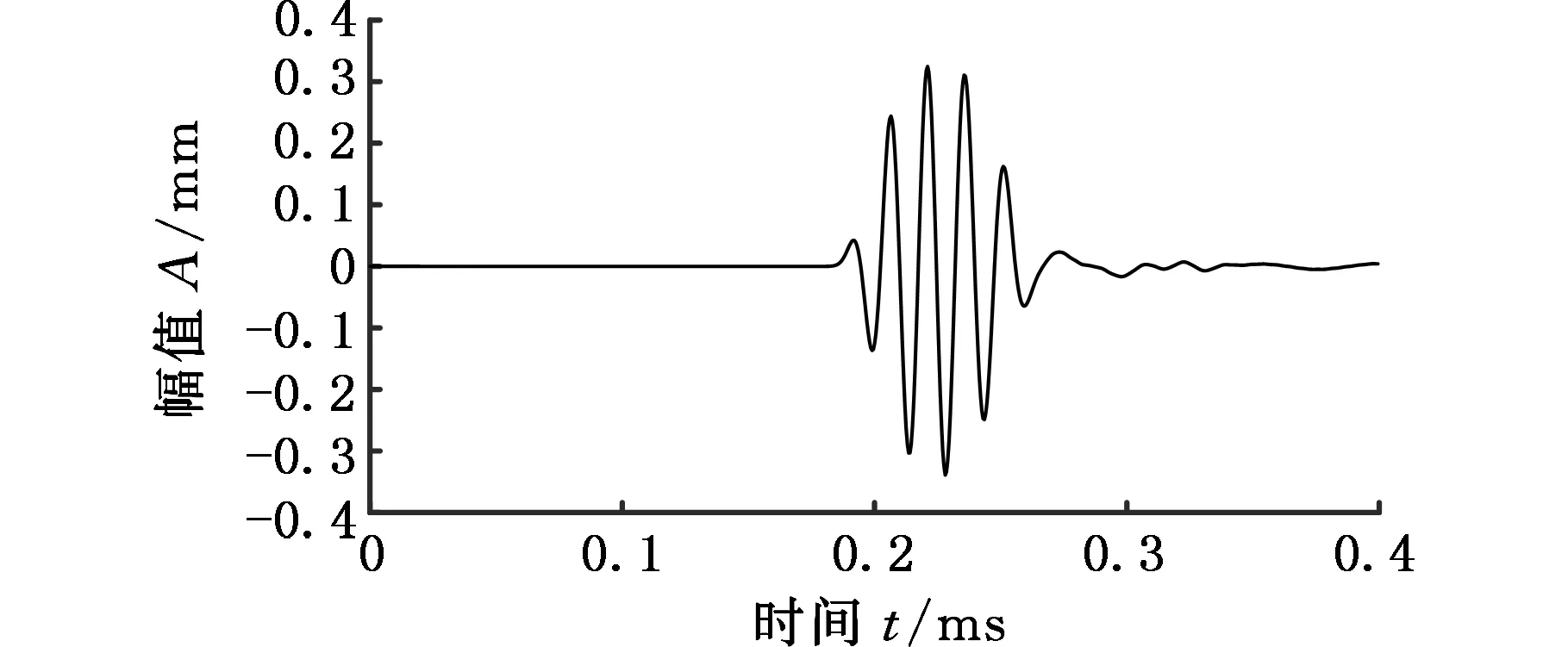
(b)p=2 MPa

(c)p=4 MPa

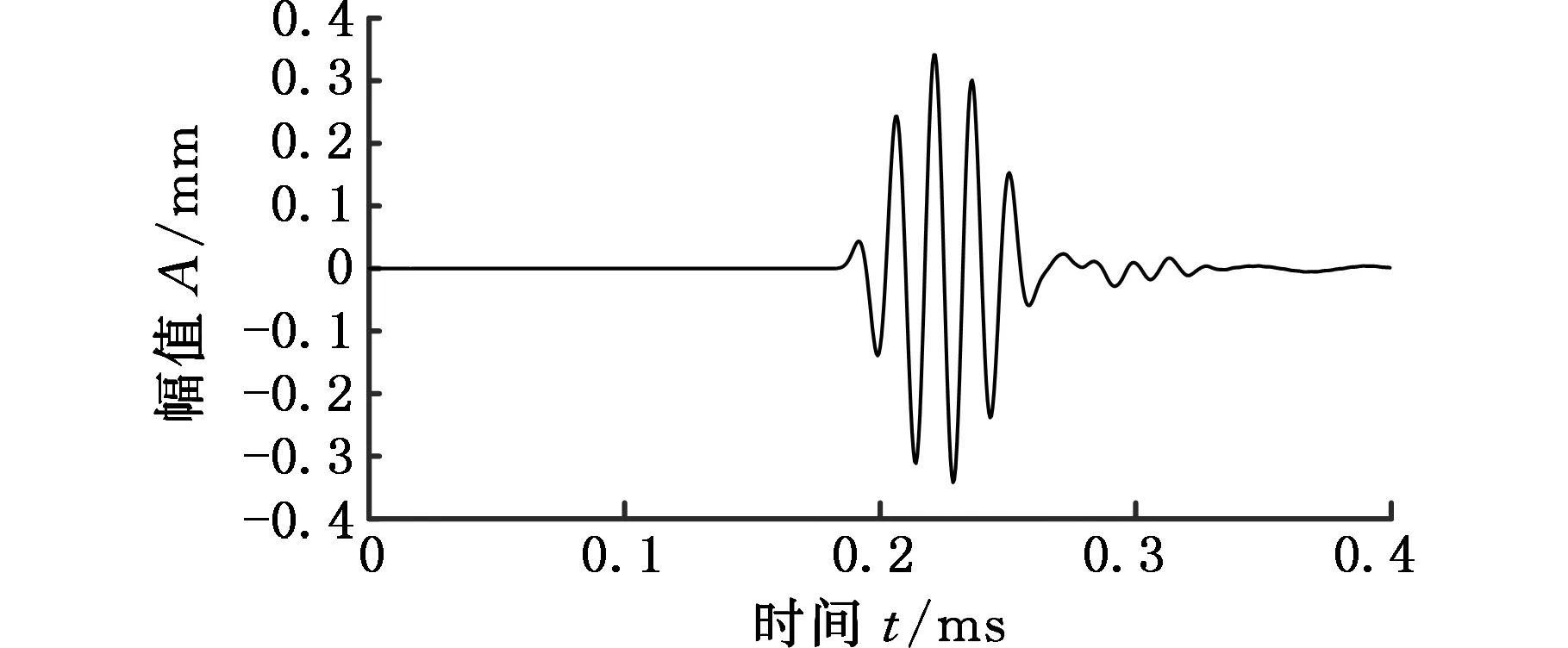
(d)p=6 MPa

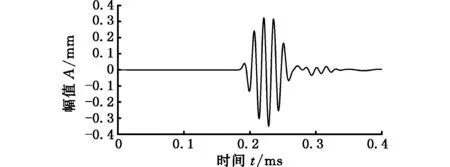
(e)p=8 MPa图3 不同管内压力时的有限元模拟结果Fig.3 Finite element simulation results of different pipe pressure

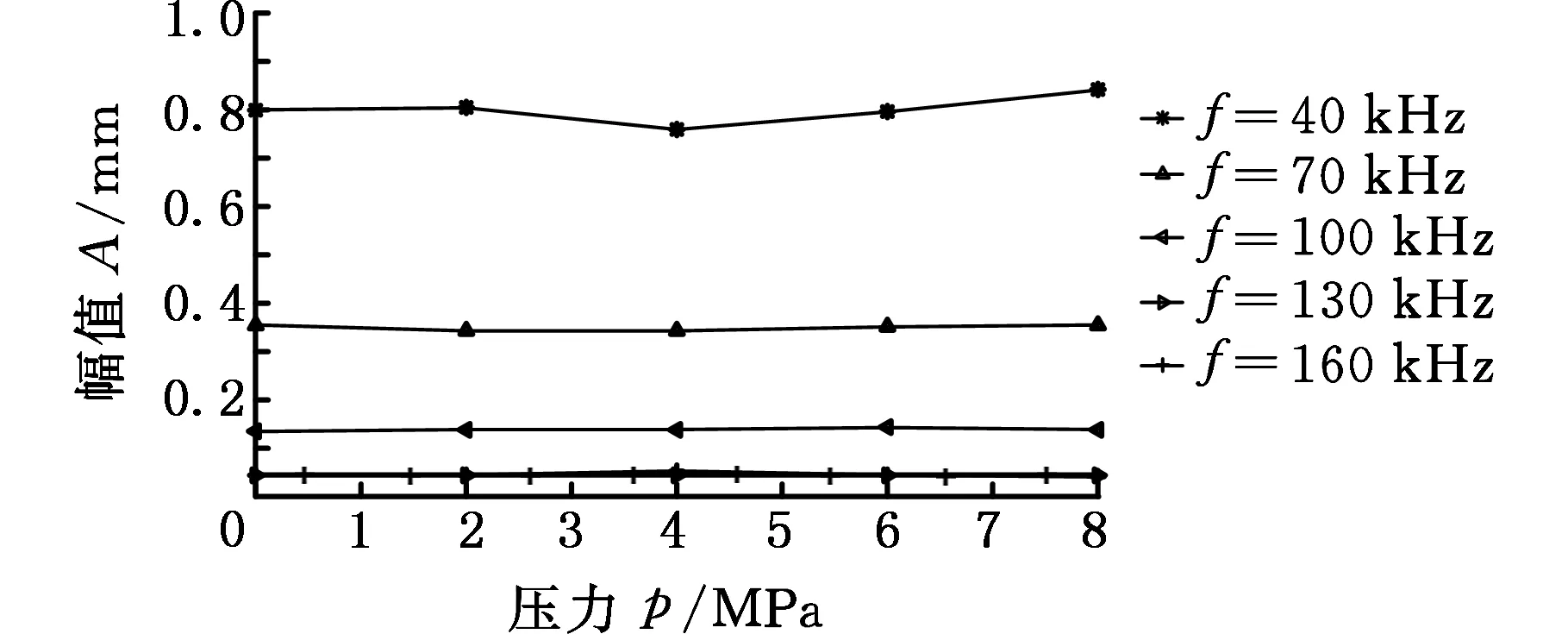
图4 不同频率情况下不同管内压力导波幅值变化Fig.4 The guided wave amplitude changes of pipe pressure in different frequency

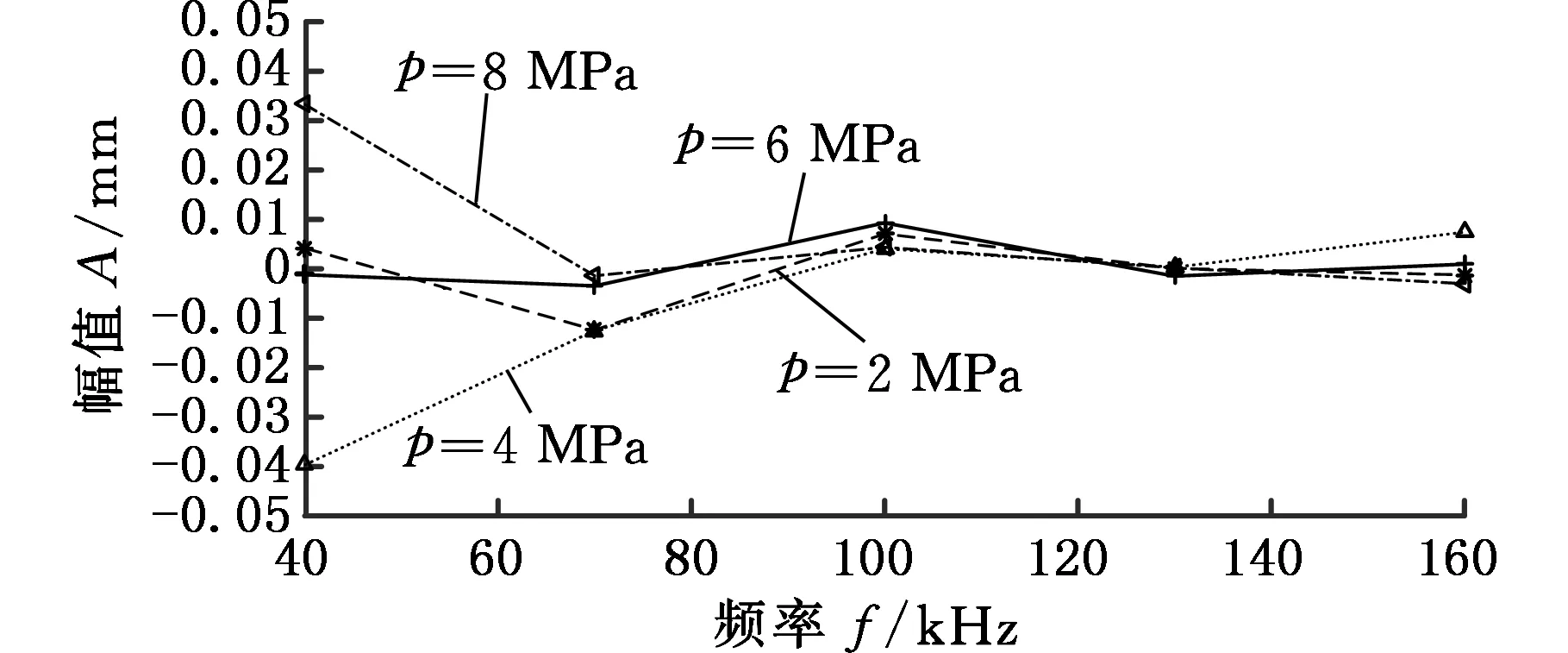
图5 不同压力情况下不同频率导波幅值变化Fig.5 Guided wave amplitude changes of different frequency in different pressure

分别提取激励频率为40 kHz、70 kHz、100 kHz、130 kHz、160 kHz时不同管内压力的回波峰值。图4所示为不同频率下管内压力变化时的幅值变化情况。考虑在同一管内压力下随频率增加导波幅值会变化的情况，需要将管内介质对导波传播能量的吸收作用消除，因此应将2 MPa、4 MPa、6 MPa、8 MPa压力下的导波峰值减去管内无压力时的导波峰值来抵消管内介质的能量吸收效应。图5所示为不同压力下随激励频率变化的幅值变化情况。

由图4和图5的模拟结果可以看出：

(1)随着频率的增大，在充有介质的管道中传播的超声导波衰减增大，衰减主要是由于管内介质对导波能量的吸收造成的。

(2)在同一频率情况下，随着管内压力的逐渐增大，管道内传播的超声导波幅值基本不变，表明导波幅值基本不随管内压力的变化而衰减。

(3)在同一压力情况下，随着激励频率的增大，管内传播的超声导波幅值变化基本相同，表明管内介质压力引起的导波幅值基本不随频率的变化而变化。

3 实验验证

为了验证有限元模拟的结果，本文制作了压力管道试件用于模拟实际充液管道状态来开展超声导波检测研究。试验的管道几何尺寸与有限元仿真的管道几何尺寸相同，管道材料也相同。管道为压力管道，图6为制作的压力管道实物图，压力表用来实时显示管体内压力值大小，泄压阀是一种保护装置，用来防止压力过大产生爆管等危害。实验过程中，管道一端配置DSB-40型电动试压泵，利用该加压试验机向压力管道内加压，管道内压力由管道上安装的压力表进行实时显示，最大可充压力为9 MPa，且与工程压力管道内压力相同。根据实际需要，压力管道内可充入液体或气体介质，液体充入量可充满也可部分充入。实验用激励信号为单音频正弦信号，激励频率可调，超声换能器沿管道一端周向均匀布置用来激励出轴对称模态。在管道另一端布置超声换能器用来接收超声导波信号，接收换能器距发射换能器的距离为600 mm。图7为实验装置示意图。

图6 压力管道实物图Fig.6 Ghysical picture of pressure pipeline

图7 实验装置示意图Fig.7 Schematic diagram of experiment device

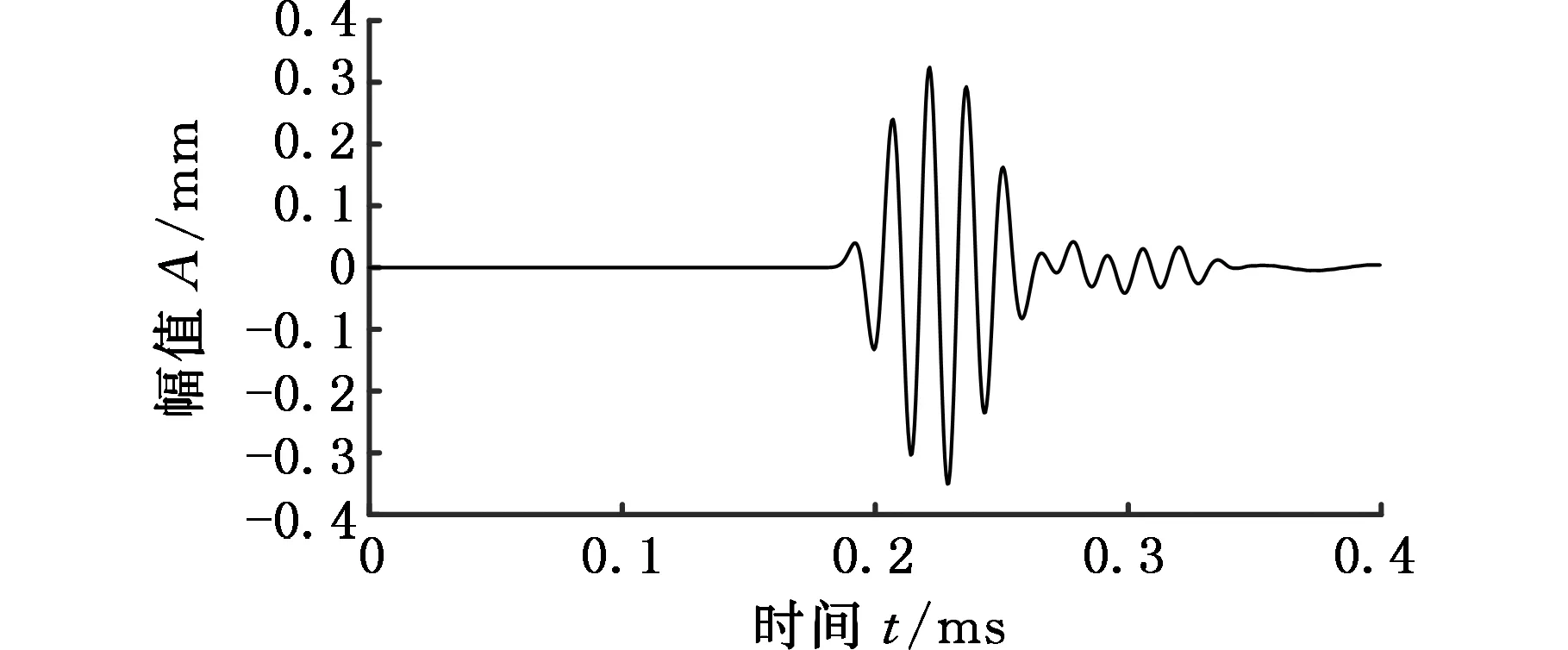
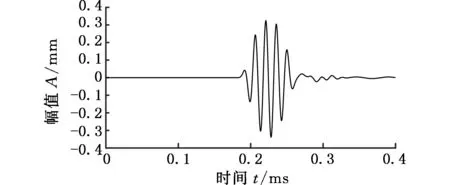
实验中将电动试压泵接入压力管道，在压力泵中装入水，并开启压力泵，根据压力表示数分别获得管内压力为0、1 MPa、2 MPa、3 MPa、4 MPa、5 MPa、6 MPa、7 MPa、8 MPa时的时域波形信号。图8所示为提取的管内压力为5 MPa时的L(0,2)模态时域波形。采用与有限元模拟相同的方法读取不同管内压力时回波信号纵向模态L(0,2)的峰值和传播时间，并计算导波模态传播速度和随管内压力变化的幅值衰减情况。得到传播时间为0.113 ms，经计算可得导波传播速度为5309 m/s，实验结果与理论和有限元分析结果基本相同。

通过对不同压力时的时域波形信号分析，可得不同压力时导波峰值变化情况如图9所示。

图9 不同压力时导波幅值变化情况Fig.9 Guided wave amplitude changes of at different pressure

由图8和图9的实验结果可看出，导波模态的传播速度基本不受管道内压力变化的影响，且随着管道内压力的增大，导波模态的幅值基本不变，实验结果与有限元模拟计算结果基本一致。

4 结论

本文采用数值模拟和实验研究相结合的方法分析了纵模超声导波在压力管道中的传播特性，研究了管内介质压力对纵波导波传播的影响。结果表明，管道内有压力比无压力时导波能量明显衰减；但随着管内压力的逐渐增大，导波能量衰减基本不随压力的增大而变化，也不随导波激励频率的增大而变化，这为超声导波技术应用于各类工程压力管道实际检测提供了理论指导。

[1] LOWE M J S, ALLEYNE D N, CAWLEY P. Defect Detection in Pipes Using Guided Waves[J]. Ultrasonics,1998,36(1/5):147-154.

[2] SHIN H J, ROSE J L. Guided Wave Tuning Principles for Defect Detection in Tubing[J]. Journal of Nondestructive Evaluation，1998,17(1):27-36.

[3] ALLEYNE D N, LOWE M J S, CAWLEY P. The Reflection of Guided Waves from Circumferential Notches in Pipes[J]. Journal of Applied Mechanics-Transactions of the ASME,1998,65(3):635-641.

[4] ROSE J L. Guided Wave Nuances for Ultrasonic Nondestructive Evaluation[J]. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control,2000,47(3):575-583.

[5] ARISTEGUI C, LOWE M J S, CAWLEY P. Guided Waves in Fluid-filled Pipes Surrounded by Different Fluids[J]. Ultrasonics,2001,39(5):367-375.

[6] LONG R, LOWE M, CAWLEY P. Attenuation Characteristics of the Fundamental Modes That Propagate in Buried Iron Water Pipes[J]. Ultrasonics,2003,41(7):509-519.

[7] CHENG J W, YANG S K, CHIU S M. The Use of Guided Waves for Detecting Discontinuities in Fluid-filled Pipes[J]. Materials Evaluation,2007,65(11):1129-1134.

[8] GALAN J M, ABASCAL R. Remote Characterization of Defects in Plates with Viscoelastic Coatings Using Guided Waves[J]. Ultrasonics,2004,42(1/9):877-882.

[9] KWUN H, KIM S Y, CHOI M S, et al. Torsional Guided-wave Attenuation in Coal-tar-enamel-coated, Buried Piping[J]. NDT & E International,2004,37(8):663-665.

[10] JIA H, JING M, JOSEPH L R. Guided Wave Propagation in Single and Double Layer Hollow Cylinders Embedded in Infinite Media[J]. Journal of the Acoustical Society of America,2011,129(2):691-700.

[11] LUO W, ROSE J L, van VELSOR J K, et al. Phased-array Focusing with Longitudinal Guided Waves in a Viscoelastic Coated Hollow Cylinder[J]. American Institute of Physics,2006,25:869-876.

[12] CHENG J W, YANG S K, LI B H. Torsional Guided Wave Attenuation in Buried Pipe[J]. Materials Evaluation,2006,64(4):412-416.

[13] AHMAD R, BANERJEE S, KUNDU T. Pipe Wall Damage Detection in Buried Pipes Using Guided Waves[J]. Journal of Pressure Vessel Technology-transactions of the ASME,2009,131(1):1-10.

[14] LEE J, NA W B, SHIN S W, et al. Parametric Density Concept for Guided Wave Attenuation Calculation in Fluid-filled and Buried Steel Pipes[J]. Advanced Science Letters,2011,4(4/5):1702-1705.

[15] DENG Q T, YANG Z C. Wave Propagation Analysis in Buried Pipe Conveying Fluid[J]. Applied Mathematical Modelling,2013,37(9):6225-6233.

[16] ROSE J L. Ultrasonic Waves in Solid Media[M]. Cambridge: Cambridge University Press,1999:1-126.

[17] SATO H, OGISO H. Guided Waves Propagating in a Water-filled Stainless Steel Pipe[J]. Japanese Journal of Applied Physics,2014,53(7):1-5.

[18] 沈立华，王悦民，郑明雪，等. 基于磁致伸缩效应导波的数值模拟和实验研究[J]. 中国机械工程,2007,18(5):532-535.

SHEN Lihua, WANG Yuemin, ZHENG Mingxue, et al. Numerical Simulation and Experimental Research on Guided Waves Based on Mangentostrictive Effect[J].China Mechanical Engineering,2007,18(5):532-535.

[19] 何存富，李伟，吴斌. 扭转模态导波检测管道纵向缺陷的数值模拟[J]. 北京工业大学学报.2007,33(10):1009-1013.

HE Cunfu, LI Wei, WU Bin. Numerical Simulation of Longitudinal Crack Detection in Pipes Using Ultrasonic Guided WaveT(0,1) Mode[J]. Journal of Beijing University of Technology,2007,33(10):1009-1013.

EffectsofPipePressuresonLongitudinalModeGuidedWavePropagations

CAI Haichao1XU Chunguang2WANG Dongfeng3SHANG Zhendong1

1.Collaborative Innovation Center of Machinery Equipment Advanced Manufacturing, Henan University of Science and Technology, Luoyang,Henan,471003 2.School of Mechanical Engineering, Beijing Institute of Technology,Beijing,100081 3.Luoyang Bearing Science & Technology Co., Ltd., Luoyang,Henan,471039

In engineering applications, the internal walls of pipelines tended to have mediums, which might produce pressures on the pipeline walls. When the ultrasonic guided wave technique was revealed to detect these pipelines, medium pressures whether or not to have effects on the propagation characteristics of ultrasonic guided wave were a very important problem. Liquid medium pressures in the pipelines were studied herein on the influences of ultrasonic guided wave propagation through numerical simulation method, guided wave attenuation properties in the different excitation frequencies and medium pressures were analyzed, and pressure pipeline experimental system was set up. The experimental results show that the ultrasonic guided wave propagation in the pipes does not change with the changes of inside pressures.

pipe; pressure; longitudinal mode guided wave; propagation characteristics

signal waveform at 5 MPa pressure

TB599

10.3969/j.issn.1004-132X.2017.23.002

2017-02-14

国家重大科技专项(2011ZX04014-081)

(编辑胡佳慧)

蔡海潮，男，1980年生。河南科技大学机电工程学院讲师、博士。主要研究方向为超声、声发射无损检测。出版专著3部，发表论文10余篇。E-mail：chclovely99@163.com。徐春广，男，1964年生。北京理工大学机械与车辆学院教授、博士研究生导师。王东峰，男，1980年生。洛阳轴研科技股份有限公司高级工程师。尚振东，男，1968年生。河南科技大学机电工程学院副教授。