遗传算法在跨超声速风洞总压控制中的应用
2017-12-15,,,
,,,
(中国空气动力研究与发展中心高速所,四川 绵阳 621000)
遗传算法在跨超声速风洞总压控制中的应用
王博文,黄叙辉,秦建华,唐亮
(中国空气动力研究与发展中心高速所,四川绵阳621000)
总压作为风洞控制中的重要流场参数,其调节性能是风洞控制系统能否满足试验要求的重要指标,为提高跨超声速风洞的总压控制水平,需对总压控制策略进行设计;针对某跨超声速风洞对总压控制系统提出的快速性和精确性要求,提出串级控制、智能PID控制和总压分段控制等方法,并利用MATLAB系统辨识工具箱对流场调节阶段的总压系统模型进行了辨识;提出将遗传算法应用于风洞流场调节阶段的PID控制器参数整定中,重点对基于遗传算法的PID控制原理和参数整定步骤进行介绍,并针对遗传算法的遗传算子进行了设计;系统仿真和风洞实际运行情况表明:该方法较常规PID参数整定与优化方法,具有更好的控制性能指标,满足总压控制系统精确性、快速性、鲁棒性等要求,为后续风洞建设和设备改造提供了新方法。
风洞;总压;遗传算法;参数整定
0 引言
跨超声速风洞控制系统作为风洞设备的核心,是提高风洞试验能力的基础。因此在风洞应用领域日趋广泛的今天,结合风洞运行和建设的经验,设计满足准确性、可靠性和稳定性要求的风洞控制系统显得尤为重要。总压作为风洞控制系统中的重要系统参数,其控制效果的优劣是风洞控制系统是否先进的重要标志。为提高风洞的总压控制水平,需要对PID控制器进行设计和参数整定。工程上通常采用常规的PID参数整定方法,该方法多采用试凑的形式,不仅会耗费大量的时间和资源,而且无法满足新风洞日益严苛的总压控制精度要求。因此采用更为智能的PID参数整定方法对总压控制器进行优化显得尤为重要。
遗传算法[1]GA(Genetic Algorithm)由美国Michigan大学的J.Holland教授于1962年首先提出,是一种模拟自然界生物进化理论和遗传机制的并行随机优化搜索算法,和其他寻优算法相比,具有并行搜索、全局收敛、适应性强、鲁棒性好等特点。本文在对跨超声速风洞控制系统简要介绍的基础上,将基于遗传算法的PID参数整定方法应用于风洞总压控制器的设计中,并利用仿真分析和实际吹风效果来验证该控制器的控制效果。
1 跨超声速风洞总压控制系统
1.1 风洞总体介绍
本文以中国空气动力研究与发展中心的某暂冲式跨超声速风洞为研究对象,该风洞试验段横截面尺寸为0.6×0.6 m,试验马赫数范围为0.3~4.5。风洞主要由进气管路、多级阀门、稳定段、挠性壁喷管段、试验段、超扩段、引射进气管路、引射器等部段组成,风洞轮廓图如图1 所示。风洞控制系统的任务是完成各阀门启闭、喷管型面、栅指位置、模型姿态、超扩段开度、洞体充气密封、部段间拉紧等的控制。

图1 风洞结构轮廓图
1.2 风洞总压控制系统
总压作为风洞试验中的重要参数,其控制的准确性、稳定性和快速性是风洞试验能力的重要体现。为加快流场建立速度,提高风洞运行效率和试验经济型,同时满足对测控系统的高精度要求。该风洞运行分为启动运行阶段和流场调节阶段。在启动运行阶段采用开环调节方式迅速完成风洞内气体充压,实现风洞快速启动;充压完成后,风洞进入流场调节阶段,采用基于积分分离的PID控制和变速PID控制等智能控制方法实现风洞总压的精确控制[2]。
暂冲式风洞通过主调压阀对稳定段总压进行调节,由于风洞稳定段容积很大,同时气体具有可压缩性的特点,风洞总压的变化无法迅速的跟随主调压阀的调节,风洞总压控制属于典型的滞后系统。这样的滞后特性使得控制系统动态特性变差,最终导致系统稳定性降低,出现系统震荡等安全风险。为改善滞后特性对控制系统的影响,本系统在风洞流场调节阶段采用了如图2所示的串级控制的方法对总压进行调节[3]。

图2 风洞串级控制原理框图
从图2中可以看出,控制系统由两个回路组成。主回路是风洞流场控制系统,用于实现稳定段目标总压P0的闭环控制;副回路是主调压阀阀位S控制系统,用于实现对阀位的精确闭环控制。副回路采用响应快速的比例调节器,具有较小的纯滞后和时间常数。串级控制系统在调节过程中,当产生的干扰施加在副回路时,副回路内部对干扰产生了抑制,减小了对主回路控制参数的影响。同时由于副回路较快的响应速度改善了控制对象的特性,加快了调节过程,从而有效地克服滞后,改善过程的动态特性,提高系统的工作频率。
2 总压系统模型的建立
为了获得好的总压控制效果,通常需要进行大量的风洞试验来对流场调节阶段的总压控制器参数进行整定。这样不仅耗费了大量的调试时间和成本,而且控制精度较低,无法进一步提高风洞的总压控制水平。为了实现更好的总压控制效果,需要利用系统辨识理论首先确立总压同主调压阀阀位开度的数学模型,即对应关系式P0=f(S),从而为后续总压控制系统的PID控制器设计和参数整定提供可能。
对总压控制系统进行辨识,需首先确定系统的模型结构,跨超声速风洞控制对象的传递函数,一般可以表示为:

(1)
或者:

(2)
式中,Y(s)为被控制对象的输出;X(s)为控制量;T,T1,T2为被控制对象的时间常数;K为系统开环传递函数;τ为纯滞后时间。
系统辨识理论中指出:在对系统进行辨识时,得到的数学模型阶数越高,模型越精确,系统逼近程度越好。但是过高的模型阶数会造成系统控制器设计难度增大,同时计算复杂,实现难度较大。因此本文假设总压控制系统结构为式(2)所描述的二阶惯性加纯滞后系统,既保证了模型精度,同时便于实现。本文将系统辨识理论应用于风洞总压控制中,选取风洞马赫数为1.5的典型试验工况为研究对象,根据最小二乘法的原理,采用MATLAB系统辨识工具箱对该工况下总压系统模型进行辨识,得到马赫数1.5的情况下总压控制系统的传递函数为:

(3)
3 基于遗传算法的PID参数整定
3.1 基于遗传算法的PID控制器
遗传算法模拟自然界生物进化机制,通过对群体内所有个体进行适应度评价,并利用选择、交叉、变异等操作使得适应性高的个体得以保留,适应性低的个体被淘汰,从而不断提高群体中的个体适应度,直到满足一定要求为止。
在自动控制系统中,系统的闭环特性很大程度上取决于控制器的性能。在总压系统模型建立后,需要对总压PID控制器参数进行整定和优化,从而使闭环控制系统性能能够满足设计要求,从而实现更好的系统控制快速性和稳定性。根据不同的发展阶段,PID参数整定可以分为基于工程性试凑的常规PID参数整定和包括最优整定、基于模糊推理的整定、基于神经网络的整定和基于遗传算法的整定等多种方法在内的智能PID参数整定。
基于遗传算法的PID参数整定是将遗传算法和PID控制相结合,利用遗传算法强大的全局搜索能力,根据已经获得的被控对象的数学模型,在PID三个参数kp、ki、kd的可行域内进行寻优,目的是获得更好的PID控制效果。基于遗传算法的PID控制系统原理框图如图3所示。
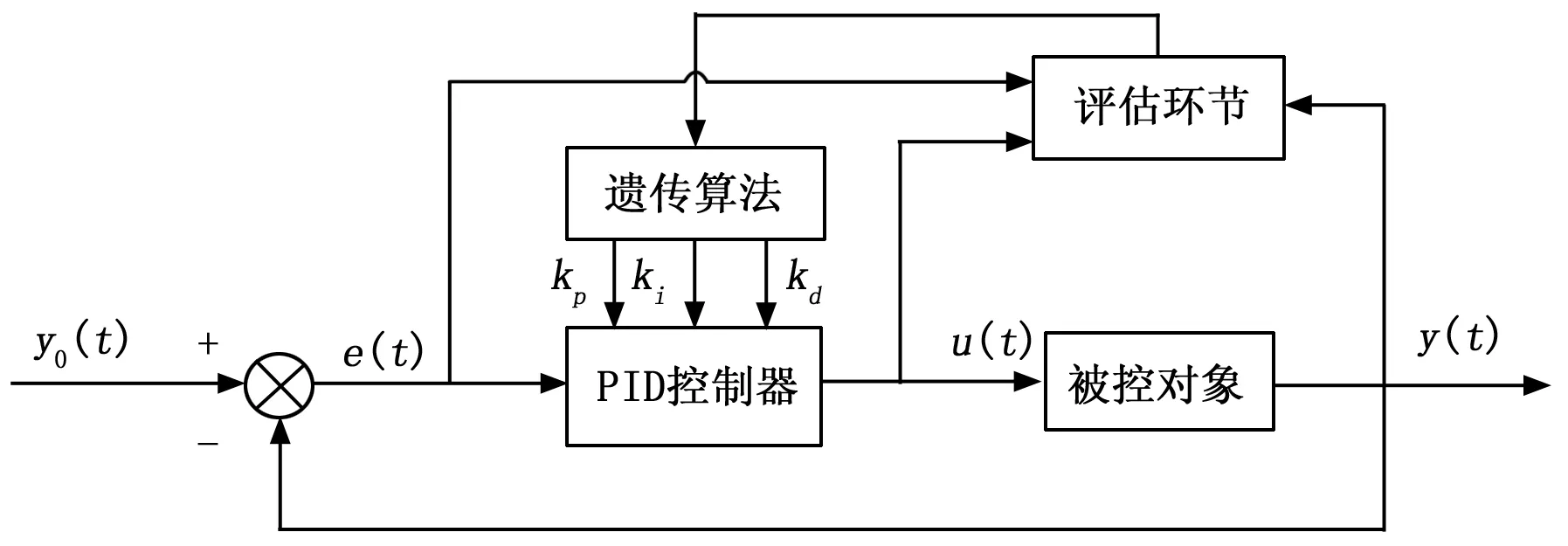
图3 基于遗传算法的PID控制原理框图
3.2 遗传算法的操作
利用遗传算法对PID参数进行整定主要包括以下几个步骤。
3.2.1 参数编码
在利用遗传算法对PID参数进行优化之前,需要首先对PID参数进行编码。针对二进制编码占用内存多,个体长度大,计算精度低,同时无法反映PID参数的实际物理含义的缺点,本文采用实数编码的方式对PID参数进行编码。
3.2.2 初始种群的生成
为了提高算法搜索效率,生成初始种群时,首先确定PID参数的取值范围,然后通过计算机随机产生代表种群中M个个体的PID参数作为初始种群。设置种群大小M=30,PID参数kp范围为[0,10],ki范围为[0,1],kd范围为[0,1]。
3.2.3 适应度函数的确定
在遗传算法中,适应度函数通常根据待优化问题的目标函数来确定。为了满足系统快速性、准确性和稳定性的要求,结合系统误差性能指标,通常采用如下的代数式作为PID参数选择的目标函数:

(4)
式中,J为目标函数值;e(t)为系统误差;u(t)为控制器输出;tu为上升时间;w1,w2,w3为各项权值。
为避免控制系统出现超调,采取惩罚机制,将超调量作为目标函数的一部分,可得改进的目标函数为:
J=
(5)
式中,ey=y(t)-y(t-1)是系统的超调量,当ey<0时表示系统出现超调。此处设置w1=0.999,w2=0.001,w3=2.0,w4=100.0。
则适应度函数可以通过下式进行表示:
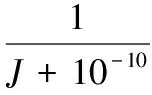
(6)
3.2.4 选择算子的改进
轮盘赌选择法是遗传算法中最为常用的选择算子[4],种群中个体被选择的概率和其适应度值成比例,个体的适应度越大,则被选择的概率越高。本文采用精英保留的策略对其进行改进。其实现过程是指对种群中适应度较高的个体不进行交叉和变异操作,并把经过交叉和变异操作后获得适应度较低的个体用其进行替换。这样就很好的保留了种群中适应度较高的个体,防止在进行交叉和变异操作时对其遗传编码造成破坏,加快了种群的进化速度,确保了算法的收敛性。
3.2.5 交叉算子和变异算子的改进
过大或过小的交叉概率Pc和变异概率Pm都会对算法造成不良影响。为此,本文对原有算法进行改进,采用了自适应遗传算法[5]。自适应遗传算法根据不同阶段种群中个体适应度的不同分布情况,自适应的改变交叉概率Pc和变异概率Pm,从而满足不同阶段的要求。自适应遗传算法的交叉概率Pc和变异概率Pm变化趋势如图4所示。

图4 自适应遗传算法Pc和Pm变化趋势图
自适应遗传算法的Pc和Pm的自适应调整公式可以表示为:
(7)
(8)
式中,F′为进行交叉操作的两个个体中较大的适应度函数值;Fmax为每代个体适应度的最大值;Favg为每代个体适应度的平均值;F为个体适应度值;Pc1,Pc2,Pm1,Pm2为交叉和变异概率值。设定Pc1=0.9,Pc2=0.5,Pm1=0.1,Pm2=0.01。
从式中可以看出,对于种群中适应度值大于种群平均适应度的个体,采用较小的交叉概率Pc和变异概率Pm,则保护这样的个体能够更好的遗传到下一代中;对于种群中适应度值小于种群平均适应度的个体,采用较大的交叉概率Pc和变异概率Pm,通过随后的交叉和变异操作使这样的个体被淘汰。同时可以看出,当被选择的个体适应度接近于种群中最大适应度值时,交叉概率Pc和变异概率Pm并不为零,这就保证了在种群进化初期,即使是适应度值最高的个体也能够以较低的概率进行进化,防止算法出现“早熟”现象,最终收敛于局部最优解[6]。通过这样的自适应交叉概率和变异概率设计,不仅保证了种群的多样性,而且满足算法的收敛性要求。
通过上述步骤将遗传算法应用于PID参数整定中,可以得到基于遗传算法的PID参数整定操作流程如图5所示。

图5 基于遗传算法的PID参数整定流程图
4 仿真分析
在某跨超声速风洞调试试验阶段,工程人员经过多次吹风试验,利用常规PID参数整定方法获得了总压控制系统的控制参数,获得了较为理想的控制效果。本文在已获得参数的基础上,利用遗传算法对PID参数进行优化。选取风洞Ma=1.5的典型工况,则此时总压控制系统的数学模型为式(3)所示。根据第3章节中介绍的PID控制器参数整定原理和图5所示的参数整定流程图来编写PID参数整定程序,可以得到如下结果:kp=0.73;ki=0.56;kd=0.03。
利用MATLAB/Simulink工具分别对PID参数优化前后的总压控制系统进行仿真,得到的闭环阶跃响应分别如图6所示。
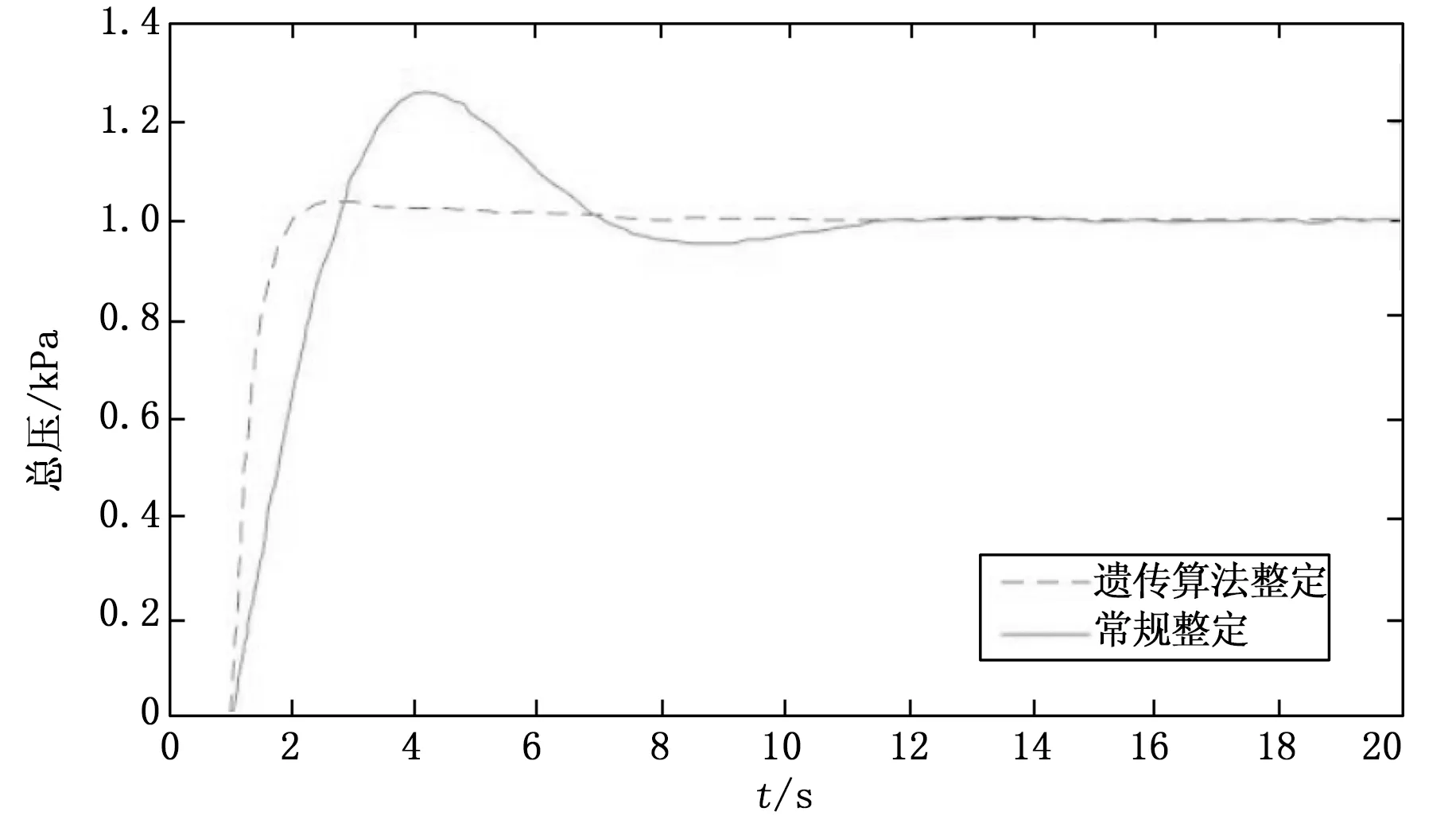
图6 总压阶跃响应曲线
比较图中两条曲线可以看出,采用常规PID参数整定方法上升时间为4 s,超调量为28%,9 s后系统达到稳定。采用基于遗传算法的PID参数整定方法上升时间为2 s,超调量5%,4 s后系统达到稳定,由此可见各方面控制性能都得到了显著提升,验证了利用遗传算法对PID参数进行整定的正确性。
5 风洞实际运行情况
在完成风洞总压控制系统和PID控制器设计后,对风洞进行吹风试验。选取本文研究的马赫数为1.5的风洞典型工况作为试验条件,同时将风洞攻角机构在-8°~16°范围内以2°为阶梯进行调节。对得到的吹风数据进行分析。
为研究风洞试验中的总压控制精度,对试验的总压误差进行比较分析。根据总压控制系统的设计技术指标,当总压相对误差达到0.2%时,认为总压已达到稳定状态。总压的误差可通过下式表示:
δ=(P0目标-P0实际)/P0目标
(9)
将风洞试验阶段总压的相对误差进行计算,得到利用遗传算法整定的总压误差变化情况如图7所示。

图7 风洞运行总压误差变化情况
从图中可以看出,风洞整个运行阶段总压误差波动较小;风洞启动13.5 s后,总压误差即达到控制系统设计的0.2%精度要求,调节速度较快。同时在风洞随后的运行过程中,总压时刻保持控制精度要求,体现了控制系统良好的准确性。
为研究风洞进入流场调节阶段后,PID控制器对总压的控制效果,选择主调压阀阀位曲线、总压曲线和总压稳定曲线进行对比,对比结果如图8所示。
总压稳定曲线是总压稳定的标识,表示总压已达到0.2%的精度要求。由图可以看出,风洞在启动13.5 s后总压稳定于设定的总压误差内,由此可得从第10 s接入PID控制器开始,总压调节时间为3.5 s,超调量为0.2%,表现出了良好的系统动态性能。
在风洞试验中,迎角机构角度的变化实际是对总压控制系统的一种干扰。为研究总压控制系统的抗干扰性能,选择迎角位置、总压曲线和总压稳定曲线进行对比,对比结果如图9所示。
从图中可以看出,无论是在迎角的运动阶段还是稳定阶段,总压都能时刻控制在总压误差带0.2%以内,保持风洞的稳定运行,体现了基于遗传算法的PID总压控制系统对于外界干扰的强鲁棒性和可靠性。
6 结论
本文针对跨超声速风洞总压控制系统的实际特点,将串级

图9 风洞迎角机构和总压的运行情况图
控制和智能PID控制技术引入总压控制中。在风洞的启动运行和流场调节阶段采用不同的控制方式,并利用基于遗传算法的PID参数整定对流场调节阶段的总压PID控制器参数进行整定优化。系统仿真和风洞总压实际运行情况表明:该方法较常规PID参数整定与优化方法,具有更好的控制性能指标,满足控制系统快速性和精确性要求,为风洞总压控制系统参数整定提出了新的方法。
[1] 周 明, 孙树栋. 遗传算法原理及应用 [M]. 北京: 国防工业出版社, 1993.
[2] 刘金琨. 先进PID控制MATLAB仿真[M]. 北京: 电子工业出版社, 2004.
[3] 褚卫华,汤更生,王 帆. 2×2 m超声速风洞流场控制策略研究与实现[J].实验流体力学,2012,26(5):98-102.
[4] 侯志强.基于遗传算法的PID控制参数优化在炉温监控系统中的应用[D] .长沙:中南大学,2012.
[5] 王小平,曹立明.遗传算法—理论、应用于软件实现 [M] .西安:西安交通大学出版社,2002.
[6] 孟 滔,周新志,雷印杰.基于自适应遗传算法的SVM参数优化[J].计算机测量与控制,2016,24(9).
ApplicationofGeneticAlgorithmsinTotalPressureControlSystemofTransonicandSupersonicWindTunnel
Wang Bowen, Huang Xuhui, Qin Jianhua,Tang Liang
(High Speed Institute,China Aerodynamics Research and Development Center, Mianyang 621000, China)
Total pressure is an important parameter in the wind tunnel control, and its regulation performance is an important index to meet the requirements of the control system. In order to improve the total pressure control level of transonic and supersonic wind tunnel, the total pressure control strategy needs to be designed. Aiming at the quickness and accuracy requirements of total pressure control system that has been proposed by a certain transonic and supersonic wind tunnel, we used the subsection control mode, cascade control and intelligent PID control in the control system, and proceeding the model identification of the total pressure system of flow field adjustment section by the MATLAB system identification toolbox. We put forward a new method that using the genetic algorithm in the PID controller parameter setting of the wind tunnel flow field adjustment section. The paper focuses on introducing the principle of PID control based on genetic algorithm and the parameter setting step, in addition, improving the genetic operators of genetic algorithm. System simulation and the wind tunnel operation show that this method has the better control performance than the conventional PID parameter setting and optimization method, which satisfies the requirement of control system and provides a new way in the future .
wind tunnel; total pressure; genetic algorithms; parameters tuning
2016-04-17;
2016-05-23。
王博文(1990-),男,山西长治人,助理工程师,硕士研究生,主要从事风洞测控技术方向的研究。
1671-4598(2017)11-0074-04
10.16526/j.cnki.11-4762/tp.2017.11.019
V211
A
