回归分析及其模型选择

(云南财经大学 云南 昆明 650000)

回归分析及其模型选择

金纪亮

(云南财经大学云南昆明650000)

在数据分析中,经常会看到数据和数据之间存在一定的线性关系.回归分析是线性中常见的一种模型,他主要刻画变量与变量之间的依赖关系,主要包括一元线性回归,多元线性回归等.本篇文章首先介绍回归分析及模型选择原理;其次利用交叉验证方法进行模型选择并介绍其在机器学习中的应用;最后进行方法总结.

回归分析；交叉验证；模型选择；机器学习

近年来随着社会的发展,数据分析的理论及实践都有了巨大的发展,特别是在经济学,数据挖掘和机器学习等方向进步巨大且应用广泛.在数据分析中,经常会看到数据和数据之间存在一定的线性关系,在处理线性关系的数据中回归分析是一种常见且简单的分析方法,许多非线性的模型转换为线性回归就会变得很简单,所以研究回归分析还是很有必要的.其次对数据建模时我们经常要考虑多个模型和多种参数估计方法,然后考虑哪种模型和方法是最为合适,这就需要我们对模型进和方法行比较分析和选择,而交叉验证法是模型选择应用最广泛的方法.

一、回归分析及交叉验证法的原理

关于回归分析和交叉验证法的研究,已经有了许多成果并被广泛应用,关于线性模型及回归分析的文献有很多,王松桂,史建红等在文献[1]中进行了详细的介绍与论证,包括模型分类,参数估计,方差分析及检验等.对β的估计上,给出了最小二乘估计,约束最小二乘估计及广义最小二乘估计,并讨论了估计的稳健性等.常用的参数估计方法是最小二乘法和最大似然估计.本篇文章所采用的参数估计方法为最小二乘法,除此之外本篇文章还引用了另一种分析方法岭回归法(λ的取值方法具体见文献2).

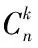
二、回归分析及其模型选择具体应用

该数据源自一组乙炔的反应数据,总共有16个观测值,其中,响应变量向量y是正庚烷(n-heptane)转化为乙炔(acetylene)的转化百分比,自变量x1是反应釜的温度(摄氏),x2是氢气-乙炔转化百分比,x3是接触时间(单位是秒).

表1 乙炔反应数据表

经过简单作图我们可以看出y与x1,x2,x3之间的关系均是线性的,所以我们建立以下线性模型：

y=β0+β1x1+ε1(1)y=β0+β1x2+ε2

(2)

y=β0+β1x3+ε3(3)y=β0+β1x1+β2x2+ε4

(4)

y=β0+β1x1+β3x3+ε5(5)y=β0+β2x2+β3x3+ε6

(6)

y=β0+β1x1+β2x2+β3x3+ε7(7)

记上述七个公式为模型1-7,对模型中的参数β的估计我们采用最小二乘法,用留一交叉验证法求出模型的均方误差记为CVi,i=1,2…7,用岭估计的方法对参数β进行估计计算出来的偏差,记作CVi′,i=1,2…7,结果为:

表2 参数估计均方误差

由上表可以看出,在岭回归法下求出的偏差CVi′与在最小二乘法下求出的偏差CVi相差不大,都是模型1最理想,模型2最不理想.在岭回归下求得的CVi′,i=1,2,3,4,6要比在最小二乘法下求得的CVi,i=1,2,3,4,6大一些,而CV6′,CV7′要比CV6,CV7小一些.然而事实上,正庚烷(n-heptane)转化为乙炔(acetylene)的转化百分比不仅仅只与反应釜的温度有关,所以我们不能说模型1在实际中就是最好的,且通过作图知响应变量y与自变量x1,x2,x3都有一定的线性关系,个人认为模型7也是可以接受的,综合考虑了所有因素,显然此时岭回归法要比最小二乘法效果好一些.

以上7个模型都只是考虑了响应变量与单一自变量之间的线性关系,没有考虑自变量之间的相互关系,所以建立模型8,在模型8中加入自变量之间的交互项.

y=β0+β1x1+β2x2+β3x3+β4x1x2+β5x1x3+β6x2x3+ε7

(8)

经过以上分析后,我们知道模型8是所得的最好的回归模型,除了经典回归外,我们用机器学习方法来对模型进行分析,看结果是否一致.此处采用机器学习中的mboost,bagging,随机森林(RF)，支持向量机等方法(SVM),采用五折交叉验证法,具体结果如下：

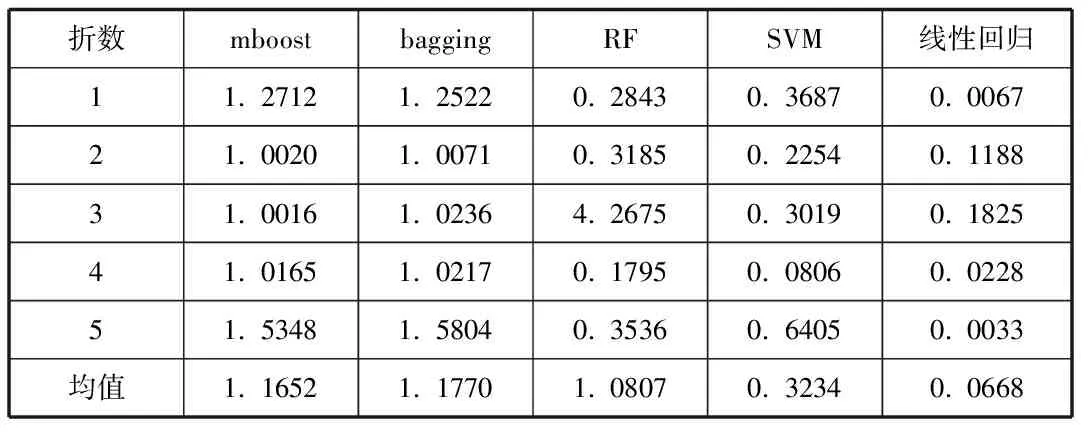
表3 模型8五折交叉验证结果表

由上交叉验证结果表可以看出此时,模型8线性回归结果非常好,结果远远小于1.线性回归和支持向量机回归结果相对其三个方法来说是好的,而mboost和随机森林,bagging回归方法是最不好的.综合几种方法比较做出的结果,还是模型8比较好,精确,方法也是线性回归的方法要精确的多,与前边的结果一致.由以上分析,我们可以认为模型8,是最好的模型,所以乙炔反应的回归模型为:

y=-262.6+0.24x1+13.97x2+1446x3-0.01x1x2-1.30x1x3-7.37x2x3

三、结论

回归模型是一种常用的模型,分析方法简单,参数估计简便,生活中好多数据都可用回归分析来解决,非线性问题也可转化为回归问题来分析.交叉验证的目的是为了得到可靠稳定的模型,它有两个明显的优点,首先在对模型选择中,每一回合中几乎所有样本数据都用于训练模型,剩下的小部分用于测试模型,所有回合结束时,所有数据都进行了训练模型和测试模型,没有数据信息的损失,因此最接近样本的真实分布,这样选择的结果比较可靠.其次实验过程当数据较少时,通过对数据的重复利用可以很好的训练模型,且在实验过程中没有随机因素影响数据,实验结果可复制.回归分析和交叉验证还有很多的研究方向,特别是在机器学习和数据挖掘方面都有很大的研究空间,这为我们今后的学习和研究指明了一个方向.

[1]王松桂,史建红,尹素菊,吴密霞.线性模型引论[M].北京:科学出版社2003.

[2]Arthur,Robert.1994.Ridge Regression:Biased Estimation for Nonorthogonal Problems University of Delaware and E.I.du Pont de Nemours amp; Co.84-86.

[3]Stone,M.Cross validatiory choice and assessment of statistical prediction.J.Roy.Statist.Soc.Ser.B,1974,36:111-147.

[4]Geisser,S.A predictive approch to the random effect moodel.Biometrika,1974,61(1):101-107.

[5]Shao,J.(1993).Linear model selection by cross-validation.Journal of the American statistical Association 88,486-494.

金纪亮(1992-),男,汉族,河南舞钢人,学生,理学硕士,云南财经大学统数学院统计学(理学)专业,研究方向医学统计。