橡胶改性水泥砂浆弹性模量预测方法
2017-12-14
(长安大学特殊地区公路工程教育部重点实验室 陕西 西安 710064)
橡胶改性水泥砂浆弹性模量预测方法
全蔚闻徐松
(长安大学特殊地区公路工程教育部重点实验室陕西西安710064)
橡胶改性水泥砂浆是一种性能优异的建筑材料,广泛应用于道路工程、港口工程和民用建筑等领域。本文基于复合材料细观力学模型,提出了橡胶改性水泥砂浆弹性模量的预测方法,并与实验结果比较,验证其合理性。
橡胶改性水泥砂浆;建筑材料;细观力学模型;模量预测
一、引言
橡胶改性水泥砂浆是一种以水泥浆为基体,集料、孔隙和橡胶为夹杂的复合材料,其抗裂、抗冻、防腐、抗渗性能优异,广泛应用于道路工程、港口工程和民用建筑等领域[1]。弹性模量作为橡胶改性水泥砂浆的基本力学参数之一,以往通常通过试验获取其具体数值[2]。于泳考虑橡胶的引起作用,建立了考虑孔隙的橡胶改性沥青砂浆弹性模量预测模型,但是其建模过程中采用了Mindness经验模型,这使得预估结果缺少理论支撑,也无法获取等效体的泊松比;除此之外,在建模过程中,其采用圆柱模型预测剪切模量,采用复合球模型预测体积模量,这使得模型假设出现矛盾[3]。因此,本文对已有模型进行改进,从细观力学模型出发,提出橡胶改性水泥砂浆弹性模量预测方法。
二、预测方法的建立
本文将橡胶改性水泥砂浆视为由水泥浆、集料、孔隙和橡胶组成的四相复合材料,分三步预测橡胶改性水泥砂浆的弹性模量。首先,将水泥石视为基体,集料视为夹杂,计算水泥砂浆等效弹性模量;然后将水泥砂浆视为基体,孔隙视为夹杂,计算含孔隙水泥砂浆等效弹性模量;最后,将含孔隙沥青砂浆视为基体,橡胶视为夹杂,计算橡胶改性水泥砂浆等效弹性模量。
(一)水泥砂浆等效弹性模量

(2.1)
由于集料的夹杂体分比较大,本文将水泥石视为基体,集料视为夹杂,采用广义自洽法预测水泥砂浆的体积模量和剪切模量[5]。首先利用弹性常数转换公式,即式(2.2)~式(2.3)将弹性模量换算为体积模量和剪切模量,再利用广义自洽模型即式(2.4)~式(2.6)计算水泥砂浆的等效体积和剪切模量,最终再利用式(2.2)~式(2.3)反算水泥砂浆等效弹性模量。
弹性常数转换公式为[5]:

(2.2)
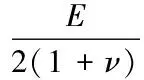
(2.3)
广义自洽法等效体积模量预测公式为[4]:
(2.4)
式中:k、μ为体积模量和剪切模量,c为体分比,角标i表示夹杂,m表示基体。
广义自洽法等效剪切模量预测公式为[5]:
(2.5)
其中,A、B、C计算公式见文献[5]。式(2.5)的解答为:

(2.6)
(二)含孔隙水泥砂浆等效弹性模量
由于孔隙体分比含量较低,本文忽略孔隙的粒径分布,将水泥砂浆视为基体,孔隙视为夹杂,采用Mori-Tanaka法计算含孔隙水泥砂浆的弹性模量。由于Mori-Tanaka法等效体积模量预测公式为广义自洽法相同[5],本文只给出其等效剪切模量计算公式:
(2.7)
由于孔隙弹性模量为0,计算过程中取夹杂体积模量与剪切模量为0,带入式进行计算。最后基于弹性常数转换公式,获取含孔隙水泥砂浆等效弹性模量。
(三)橡胶改性水泥砂浆等效弹性模量
由于橡胶掺量较低,本文将含孔隙水泥砂浆视为基体,橡胶视为夹杂,采用Mori-Tanaka方法预测橡胶改性水泥砂浆等效弹性模量[5]。其计算公式如式(2.4)和式(2.7)所示。
三、预测结果分析
采用文献[2]的数据对本文建立的方法进行验证。文献三采用的配合比参数和材料力学参数分别如表3.1和表3.2所示。
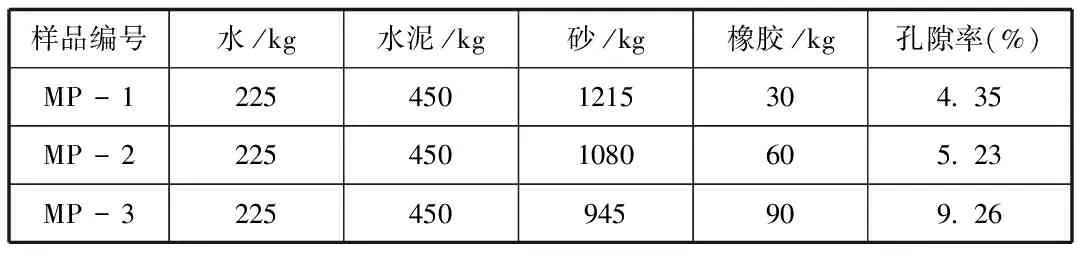
表3.1 配合比参数

表3.2 材料力学参数
将表3.1和表3.2数据带入本文建立的方法,最终得到的预测结果如表3.3所示。由表3.3可知,本文提出的方法可以较准确的预测橡胶改性水泥砂浆的弹性常数,且随着孔隙率的增加,本文提出的预测方法较文献[3]更优。

表3.3 本文预测结果和试验结果
四、结论
本文基于细观力学模型中的广义自洽模型和Mori-Tanaka模型,预测了橡胶改性水泥的弹性模量。结果表明,本文建立的方法预测精度较高,与其他方法相比,其方便、经济、理论基础牢固、精确度较高,具有较大的推广价值。
[1]刘春生,朱涵,李志国等.橡胶细集料水泥砂浆基本性能研究[J].混凝土,2005,89(07):38-42.
[2]李红燕.橡胶改性水泥基材料的性能研究[D].东南大学硕士学位论文,2004.
[3]于泳,朱涵,朱学超等.孔隙对橡胶集料水泥砂浆弹性模量预测模型的影响[J].硅酸盐通报,2015,34(3):892-896.
[4]万赟,刘加平,洪锦祥.用多层次二元复合法则计算高强CA砂浆弹性模量[J].硅酸盐学报,2014,42(2):199-202.
[5]张研,韩林.细观力学基础[M].北京:科学出版社,2014.
全蔚闻(1993-),男,长安大学特殊地区公路工程教育部重点实验室,研究生。
