无压输水系统水流过渡时间的影响因素探究

张巧丽 周建旭

(河海大学 水利水电学院， 南京 210098)

无压输水系统水流过渡时间的影响因素探究

张巧丽 周建旭

(河海大学 水利水电学院， 南京 210098)

为探究进口闸门开启时间和无压引水隧洞长度对无压输水系统水流过渡时间的影响，基于一维明渠非恒定流特征线法，并结合隐式差分法，建立“水库+无压引水隧洞+沉沙池”数值仿真分析模型，对含有沉沙池的无压输水系统的瞬变流过程进行了数值模拟．结果表明，进口闸门开启时间与无压引水隧洞长度均为影响系统水流过渡时间的敏感性因素．

无压输水系统； 瞬变流； 数值模拟； 过渡时间

无压输水是长距离供水的一种常用型式，明渠引水和无压隧洞引水是常用的引水方式．在输水系统受到外界干扰引用流量发生改变时，会发生水力过渡过程，即瞬变流．在实际工程中，水力过渡过程会影响工程的运行效率及安全稳定性．对于含有隧洞的无压输水系统的水力过渡过程，众多学者都对其进行了研究．柳园园等[1]修正了Preissmann窄缝假定方法中的窄缝宽度公式，建立明渠和有压管道瞬变流分析的通用模型，实现城市排水管网明满过渡流的有效数值模拟．杨开林[2]研究了国内外在明渠非恒定流理论和方法方面的研究进展，着重指出如何准确的模拟明满交替流及其特征现象仍然是研究的难点．相较而言，对水力过渡时间的研究主要是针对灌溉渠系的输水渠道，周美林等[3]以灌溉渠道中的梯形断面渠道，研究了渠长、调控时间、流量变化率等对过渡时间的影响．范杰[4]等对南水北调中线工程渠首段非恒定流水力学响应时间进行了研究．关于水力过渡时间的研究大都针对简单明渠渠道，本文以含有无压引水隧洞和沉沙池的无压输水系统为研究对象，通过数值模拟展开对水力过渡时间的研究．

1 计算方法

明渠的非恒定流理论是无压输水系统瞬变流分析的基础，其基本方程是圣维南方程组，常用的求解方法是特征线法与隐式差分法，本文主要采用特征线法，在进行节点分析时采用了隐式差分法．

1.1 特征线方程

无压隧洞水力过渡过程满足一维明渠非恒定流特征线方程，即圣维南方程组：

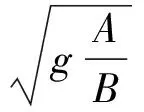
式中，V为引水隧洞中水流流速；y为引水隧洞水深；g重力加速度；Sf为能量坡度；S0为隧洞底坡；x为隧洞长度；c为隧洞水面波速；A为隧洞过水断面面积；B为隧洞水面宽度．

将圣维南方程组分别沿正、负特征线积分，可得特征线方程为

式中，Cp、Cm、Bm、Bm均为中间计算量，由前一时刻的计算结果确定；vp、vm分别为P、M断面的平均流速；yp为P断面水深．

1.2 隐式差分法

基于明渠水流的连续方程和动量方程，结合各偏导项不同的差分格式，建立迭代收敛性较优的明渠水流瞬变流求解方法-特征隐式格式法[5-6]，推导得到的特征描述方程为

式中，h和Q分别为各计算断面的瞬时水深和流量，下标m-1、m、m+1表示断面位置；系数ai、bi、ci、di(i=1，2)和ei右端项(i=1，2)由相关断面的参数计算确定．

引入各计算断面瞬时水深和流量的增量表示形式，式(5)和(6)经过Newton-Raphson法线性化，可得

式中，Δh和ΔQ分别为各计算断面的水深增量和流量增量；aim、bim、cim、dim、eim(i=1，2)分别为各项系数和右端项，采用双下标表示，其中第二个下标m表示计算断面位置．

2 工程实例

2.1 工程概况

某引水工程由取水口进水塔、无压引水隧洞、沉沙池、引水明渠、压力前池等建筑物组成．自水库取水口取水，进水塔引水方式为无压引水，取水口由闸门控制，在某段时间内闸门开度由零线性增加到0.6．水库正常蓄水位为830.57 m，无压引水隧洞总长约为600 m，采用城门洞型断面，净宽5m，直墙段高5.0 m，拱高2.5 m，坡降为1/3 000，糙率为0.013，无压引水隧洞进口底部高程为826.00 m．隧洞出口接双室式沉沙池，沉沙池分为两室，中间以孔口连接，孔口面积为20 m2．沉沙池2号沉沙室出口设有溢流堰，溢流堰底部高程为821.92 m，堰顶高程为829.50 m，堰宽1 400 m，该系统的设计运行流量为23.55 m3/s．

2.2 瞬变流计算模型分析

2.2.1 初始条件分析

本文采用解棱柱体明渠恒定渐变流微分方程的方法来确定无压引水隧洞的初始恒定状态，其求解方程为：

水面线方程为一阶微分方程，可采用四阶龙格-库塔法求解．

2.2.2 边界条件分析

1)上游边界条件

无压引水隧洞上游接水库，可认为在过渡过程中水库水位近似保持恒定不变，隧洞进水口由取水闸门控制，忽略进口处的水头损失，则上游边界为取水口闸门边界，示意图如图1所示．

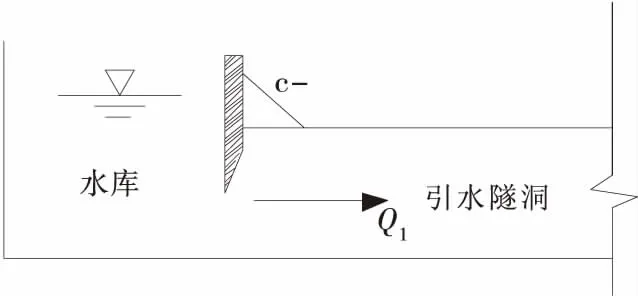
图1 水库边界示意图

边界处的相容方程为负特征线方程：

式中，y1为引水隧洞进口断面水深；V1为进口断面表面流速；Cm、Bm意义同上．

取水口闸门处，有节点控制方程：

式中，yv为水库水深，y1为引水隧洞进口断面水深；mv为闸门流量系数，取mv=0.57；F为闸门开启面积，F=By1，B为隧洞过水断面水面宽度；τ为闸门开度，Qv为闸门过流量．

引水隧洞断面流量水位关系为

式中，Qv为引水隧洞进口断面流量，A1为隧洞进口断面面积．

由连续方程即可得

对于上述方程联立，运用牛顿迭代法进行编程求解．

2)沉沙池边界条件

无压引水隧洞后接双室式沉沙池，假设隧洞出口断面没有水头损失，沉沙池两室之间以孔口相接，后室底部排沙，顶部溢流进入下游河道，不考虑泥沙作用，将其作为简单水池处理．沉沙池边界计算模型如图2所示．

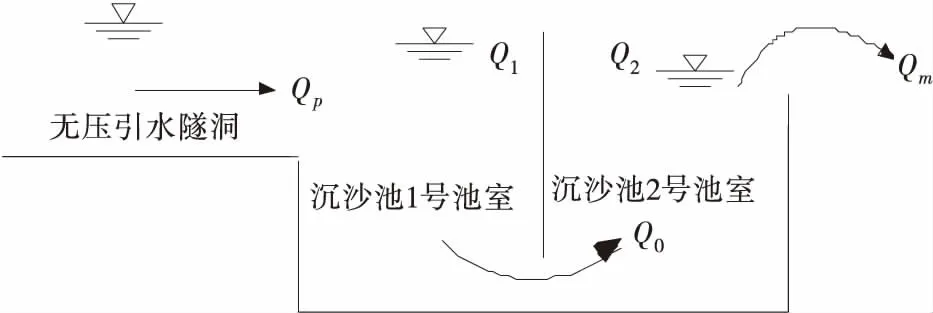
图2 沉沙池边界示意图

忽略水流从引水隧洞进入沉沙池的局部水头损失，初始时刻系统运行流量为0 m3/s，沉沙池两个池室水位齐平．

基于明渠非恒定流特征线方程，沉沙池边界处的相容方程为正特征线方程：

式中，yp为隧洞出口断面水深；Vp为隧洞出口断面波速；Cp、Bp意义同上．

对于沉沙池，其水位与流量的关系：

式中，Q1、Q2分别为进入沉沙池1号池室、2号池室的流量；Z1、Z2分别为沉沙池1号池室、2号池室的水位；A1、A2分别为两个池室的水面面积．

两池室间的孔口出流方程为：

式中，μ为孔口流量系数，μ=0.450；A为孔口面积；QK为孔口过流量．

沉沙池2号沉沙室边界处溢流公式为：

式中，m为溢流堰流量系数，m=0.340；L、Zs、Qm分别为溢流堰堰宽、顶高程及过流量．

由连续方程描述沉沙池节点的控制方程为：

式中，QP为引水隧洞出口断面的流量．

对于方程(14)～(18)，采用隐式差分法进行求解，将方程(15)两边积分并且联立可得

用牛顿-雷伏生将方程组(19)线性化求解．

2.2.3 系统运行特性分析

初始时刻水库处于正常蓄水位，闸门全关，处于恒定流状态，沉沙池2个池室水位齐平，没有水位差，孔口不过流，2号池室水位低于溢流堰堰顶高程，没有溢流．随后闸门由全关慢慢开启，系统过流量开始增加，随着通过引水隧洞断面流量的改变，隧洞内水流的水深和流速将发生改变，水流从隧洞出口断面进入沉沙池，随着来流量的增加，1号池室水位开始上升，使得两个池室之间产生水位差，所以水流开始从1号池室进入2号池室，造成2号池室水位开始上升，由于2号池室出口处接有溢流堰，当2号池室水位上升高于溢流堰堰顶高程时，沉沙池开始向下游河道溢流，溢流堰的存在限制了沉沙池水位的升高．最终系统达到稳定运行流量时，无压引水隧洞各断面水位和流速处于恒定状态，隧洞出口断面进入1号池室的流量等于通过孔口从1号池室进入2号池室的流量，进入2号池室的孔口流量又等于溢流量，2号池室的水位变化情况与孔口流量和溢流量的相对大小有关．最终系统达到稳定状态时，沉沙池的两个池室水位差保持不变，从溢流堰进入下游河道的溢流量也是固定不变的．

3 结果分析

3.1 数值模拟结果

考虑水库的正常蓄水位830.57 m，闸门全关，隧洞内水位高程为829.50 m，系统运行流量从零增加到设计运行流量23.55 m3/s，取水口闸门线性开启，60 s内开度由零增加到0.6．基于系统简化模型，采用显格式法建立瞬变流分析的数值仿真模型，开展系统瞬变流特性分析，研究无压引水隧洞进水口断面和双室式沉沙池两个池室的水力参数变化，结果如图3～4所示．

图3 进水口断面流量变化曲线

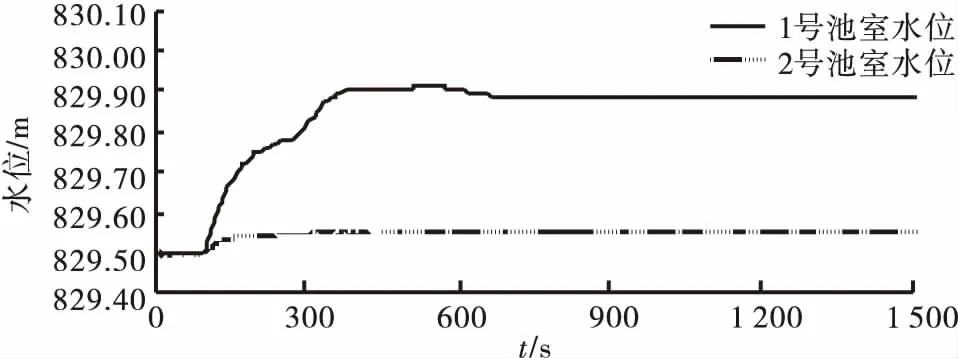
图4 沉沙池水位波动曲线

由图3可知，闸门开启后，无压引水隧洞进水口断面的流量随着时间的增加从零开始增加，呈现周期性波动，波动逐渐衰减，在267 s左右达到第一个波峰值28.93 m3/s，变化周期是167.94 s．1 673 s以后，进水口断面的流量不再变化，稳定在23.53 m3/s．

由圣维南方程组，进水口断面水流表面波速

则按照理论公式计算得到流量的变化周期是

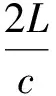
数值模拟得到的结果与理论公式计算得到的结果误差在10%以内，符合实际情况．

分析图4可得，开始的一段时间内，沉沙池两个池室的水位基本保持不变，随后，两个池室的水位均慢慢增加，相较于2号池室，1号池室水位先增加并且变化得较为明显，最终两个池室的水位均趋于稳定．

3.2 进口闸门开启时间的敏感性研究

建立边界条件时，进水口的边界控制条件是闸门，闸门的特性必然会影响进水口断面在过渡过程中流量的变化，考虑闸门开启时间，将开启时间从60 s变为180 s、360 s，研究其对进水口断面瞬变流特性的影响．

进水口的流量变化见图5、图6及表1．

图5 闸门开启时间180 s进水口断面流量变化曲线

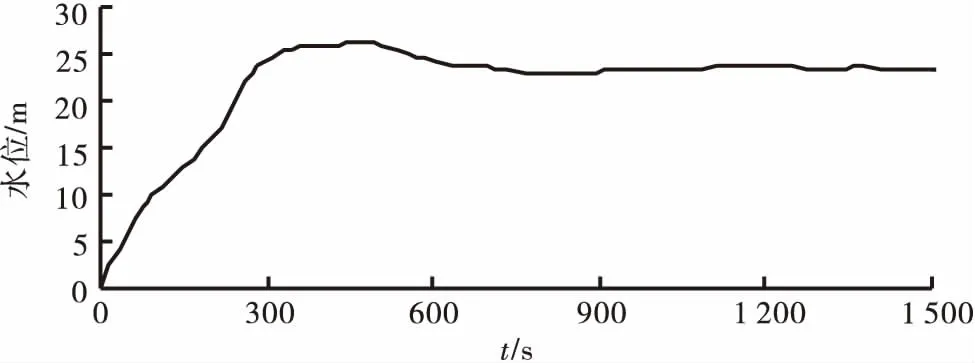
图6 闸门开启时间360 s进水口断面流量变化曲线

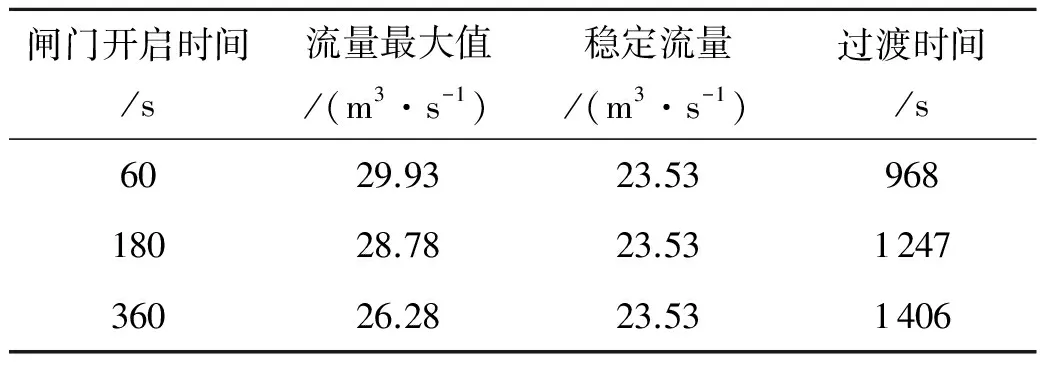
闸门开启时间/s流量最大值/(m3·s-1)稳定流量/(m3·s-1)过渡时间/s6029．9323．5396818028．7823．53124736026．2823．531406

结合图表，过渡过程的最终稳定流量和闸门开启时间无关，但闸门开启时间越长，最终达到恒定状态所需要的时间越久．在过渡过程中，闸门开启时间越短，流量峰值越大，达到时间越快，流量变化趋势较明显．

沉沙池两个池室的水位波动过程见图7、8及表2．

图7 闸门开启时间180 s沉沙池水位波动曲线

图8 闸门开启时间360 s沉沙池水位波动曲线

分析图表，闸门开启时间的变化对沉沙池的水位波动趋势影响很小，这是由于沉沙池的水面面积很大．具体分析表2中的数据，可以发现闸门开启时间发生改变时，沉沙池两个池室的最终稳定水位没有改变，因而最终向下游引水道的溢流量也没有发生改变．水位最大值变化很小，可以忽略不计，而受闸门开启时间影响较大的是系统达到稳定状态的时间，闸门开启需要的时间越久，系统达到最终稳定运行状态所需要的时间也越久．

表2 闸门开启时间对沉沙池水位波动的影响

3.3 无压引水隧洞长度的敏感性研究

在基于明渠非恒定流计算模型的无压引水隧洞的瞬变流特性分析中，需要考虑隧洞的设计参数，其不仅与系统的运行稳定性密切相关，还直接涉及工程的投资运算和经济合理性，为了保证系统能够稳定运行并且经济合理，有必要结合隧洞的设计参数进行敏感性分析．考虑隧洞的设计长度，研究其长度对系统控制断面水力参数的影响．

分别设引水隧洞长度为900 m、1 200 m，研究进口断面流量变化过程，数值模拟结果见图9、图10及表3所示．

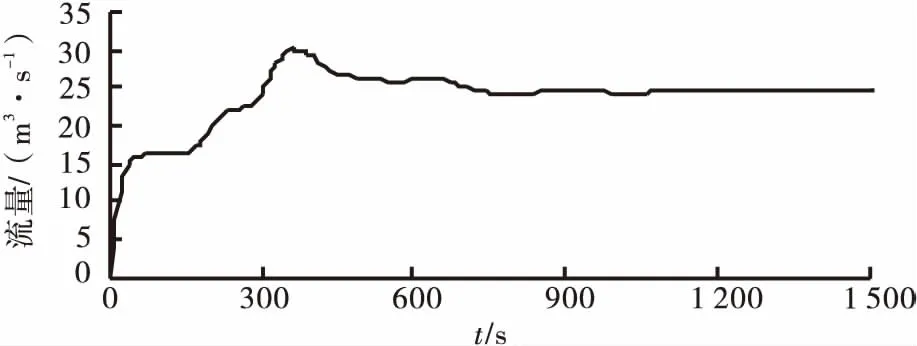
图9 L=900 m进口断面流量变化曲线

图10 L=1 200 m进口断面流量变化曲线

隧洞长度/m)流量最大值/(m3·s-1)稳定流量/(m3·s-1)过渡时间/s120032．1025．93140990030．3924．84124660029．9323．53968

分析图3、图9、图10及表3可得，隧洞长度在600 m与1 200 m之间变动时，隧洞越长，过渡过程中流量的峰值会增加．

无压隧洞长度不仅会影响进水口断面流量，也会影响沉沙池的水力特性．当隧洞长度为900 m、1 200 m时，沉沙池水位波动结果如图11、12及表4所示．

图11 L=900 m沉沙池水位波动曲线

图12 L=1 200 m沉沙池水位波动曲线

隧洞长度/m水位最大值/m1号池室2号池室稳定水位/m1号池室2号池室过渡时间/s溢流量/(m3·s-1)1200830．006829．558829．962829．553167025．92900829．956829．556829．926829．552132424．82600829．914829．553829．886829．55083723．52

结合图4、图11、图12及表中数据可得，隧洞长度在600 m与1 200 m之间改变时，沉沙池的水位波动趋势基本保持不变，过渡过程中的水位最大值随着隧洞长度的增加而增加，最终的稳定水位及最终的稳定流量也随着隧洞长度的增加而增加，系统最终达到稳定所需要的时间也随着隧洞长度的增加而增加．

4 结 论

1)相同条件下，取水口闸门开启时间越快，系统的过渡过程持续时间越短，较快趋于稳定，同时，无压隧洞过水断面会产生较为明显的流量变化．

2)相同条件下，无压引水隧洞长度越长，引水隧洞进水口断面在过渡过程中流量变化幅度越大，最终的稳定流量越大，系统达到最终恒定状态所需要的时间越长．3)由于沉沙池水面面积很大，闸门开启时间与隧洞长度对沉沙池的瞬变流特性影响较小，但是会影响沉沙池最终达到恒定状态所需要的时间，随着隧洞长度的增加或闸门开启时间的延长，沉沙池最终达到稳定水位所需要的时间亦增加．

因此，在实际运行过程中，为了避免进水口断面出现流量的急剧变化，闸门开启时间不能过短，但闸门开启时间过长，系统达到稳定状态所需要的时间也越长，因此要结合工程实际情况，适当选择闸门开启时间．同时应结合工程实际的地质地形条件，根据工程投资及系统的安全稳定要求进行综合分析，设计合理的隧洞长度．

[1] 柳园园，王船海，吴朱昊，等.城市排水管网明满交替非恒定流数学模型的研究[J]．水动力学研究与进展A辑，2016，31(2)：210-218．

[2] 杨开林.长距离输水水力控制的研究进展与前沿科学问题[J]．水利学报，2016，47(3)：424-435．

[3] 周美林，吕宏兴，王家琪，等.渠道非恒定流过渡时间影响研究[J]．灌溉排水学报，2016，35(1)：71-73，98．

[4] 范 杰，王长德，管光华，等.渠道非恒定流水力学响应研究[J]．水科学进展，2006，17(1)：55-60．

[5] 樊红刚，陈乃祥，杨 琳，等.明满交替流动计算方法研究及其实验验证[J]．工程力学，2006，23(6)：16-20．

[6] 邓命华，刘德有，周建旭.水电站变顶高尾水洞瞬变流计算及体型设计[J]．河海大学学报：自然科学版，2003，31(4)：436-439．

ResearchonInfluencingFactorsofFlowTransitionTimeinFree-flowWaterDeliverySystem

Zhang Qiaoli Zhou Jianx

(College of Water Conservancy & Hydropower Engineering, Hohai Univ., Nanjing 210098, China)

In order to study the influence of the entrance gate opening time and the length of the water diversion tunnel on the flow transition time in the free flow water delivery system, a model of transient flow of “reservoir + free flow tunnel + sand basin” is established by combining the characteristic lines with implicit difference method to do numerical simulation about transient process of the free-flow water delivery system with desilting basin. The results indicate that both the entrance gate opening time and the length of the water-diversion tunnel are sensitive factors of flow transition time.

free-flow water delivery system; hydraulic transient; numerical simulation; transition time

10.13393/j.cnki.issn.1672-948X.2017.05.006

2017-01-10

国家自然科学基金项目(51079051)；江苏高校优势学科建设工程资助项目(PAPD)

张巧丽(1990-)，女，硕士研究生，研究方向为水电站及泵站水力学．E-mail：zql12021027@163.com

TV732

A

1672-948X(2017)05-0029-05

[责任编辑王迎春]