山区峡谷陡坡急弯河道电站取水能力及水力性态研究

冯习富，余文锋

（贵州新中水工程有限公司，贵州 贵阳 550001）

1 概况

涟江海里水电站为径流式电站，位于贵州省黔南州西部惠水县断杉镇，为蒙江梯级规划涟江河段第二级。电站原装机规模为16570 kW（2×8000 kW+1×320 kW+1×250 kW）。于2017 年进行增效扩容改造后，电站总装机容量为32000 kW。

工程任务为发电。主要建设内容如下：已建大坝加固，新增放空底孔；新建发电进水口、有压引水隧洞、调压井及压力埋管；新建发电厂及升压站。

电站水库总库容98 万m3，属小（1）型电站，工程等别为Ⅳ等，大坝属4 级，电站厂房为4 级。

大坝采用C15 常态混凝土重力坝，全断面溢流。坝顶高程875.61 m 同正常蓄水位高程同高，最大坝高13.11 m。水库不具备调节能力。

进水口为洞式进水口，由取水隧洞、洞内闸室组成。引水隧洞进口位于新、老大坝之间，距新大坝直线距离20 m；取水口位于涟江转弯段凸侧，河床狭窄、纵坡较大，大坝泄洪时，坝顶水面流速大，取水口取水条件不甚理想[1]。

2 研究内容

海里水电站所在河流属山区峡谷型河道，河道两岸山体陡峭，受地形条件和已建大坝位置及施工条件限制，二厂发电引水系统采用竖井式进水口布置于左岸地下硐室内，进水口前采用圆形隧洞连接河道取水。因取水隧洞洞口位于河谷凸岸，为保证电站取水安全，需通过数值模拟或模型试验进一步验证发电引水系统首部轴线方位、结构型式及不同工况下过流能力；同时优化进水口前端隧洞设计布置及大坝体型（坝顶高程）优化，改善取水条件，保证工程取水安全。

3 进水口三维数值模拟

3.1 三维水流数学模型

项目采用三维数值模拟技术对海里电站进水口取水能力进行研究[2]。完整的N-S 方程是从数学方面来描述水流运动的基本方程，该方程要能够从本质上控制水流的的运动过程，本文的数值模拟主要采用三维紊流数学模型，控制方程包括时均的连续性方程和动量方程[3]。

紊流是自然界最常见的流体运动状态，深入了解紊流运动特性，对于研究工程中复杂水流及波动现象具有十分重要的意义。目前，紊流数值模拟方法主要包括直接数值模拟（DNS）、雷诺时均方法（RANS）与大涡模拟（LES）。雷诺时均方法（RANS）由于其独有的特点，较为广泛地应用于工程实际中，本次研究，选用RNG k-ε 湍流方程求解附加运输方程[4]。

3.2 进水口至调压井段三维计算结果

水库进水口至调压井段的数值模拟区域包括水库、进水口段、闸室段、隧洞段及调压井段等。按照1∶1 尺寸建立海里电站水库及进水口计算模型，三维计算网格类型采用非结构化与结构化网格相结合的方式。计算区域内网格单元总数接近500 万个，计算节点数为超过400 万个，单元格的体积控制在6.5×10-7m3～2.5×10-1m3之间。

图1 三维模型图

三维数值计算的进水口边界采用正常蓄水位875.61 m，进水口及隧洞的过流量为41.5 m3/s，大于设计要求的31 m3/s，进水口取水能力满足设计要求。在正常蓄水位时（875.61 m），进水口段及隧洞水流为有压流。水流进入进水口后受弯道影响，水流偏向右侧，进水口段流速在3.5 m/s 左右，隧洞段的流速在4.5 m/s 左右。隧洞中心流速大于边壁流速。

3.3 进口段三维计算结果

数值模拟区域包括水库、进水口段、闸室段、出口段及溢流坝段等。计算区域内网格单元总数为360 万个，计算节点数为230 万个，单元格的体积控制在6.88×10-7m3～2.56×10-1m3之间。

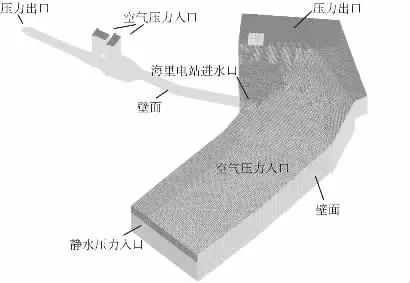
图2 进口段整体网格划分示意图

采用模型出口设置压坡（收缩面积）的方式模拟模型出口后隧洞及调压井等部位原型阻力。出口半径0.95 m 时，进水口的取水流量为31.1 m3/s，后续不同水位条件下的引水能力计算保持该出口面积不变作为出口边界条件。

数学模型计算了两种条件下进水口的取水能力，条件一溢流坝完全敞泄，条件二假定溢流坝高程为886 m，坝身不溢流，进水口的取水能力介于二者之间。各库水位对应的泄流量见表1，水位- 流量关系曲线见图3。其中电站设计洪水位883.61 m，校核洪水位885.67 m。

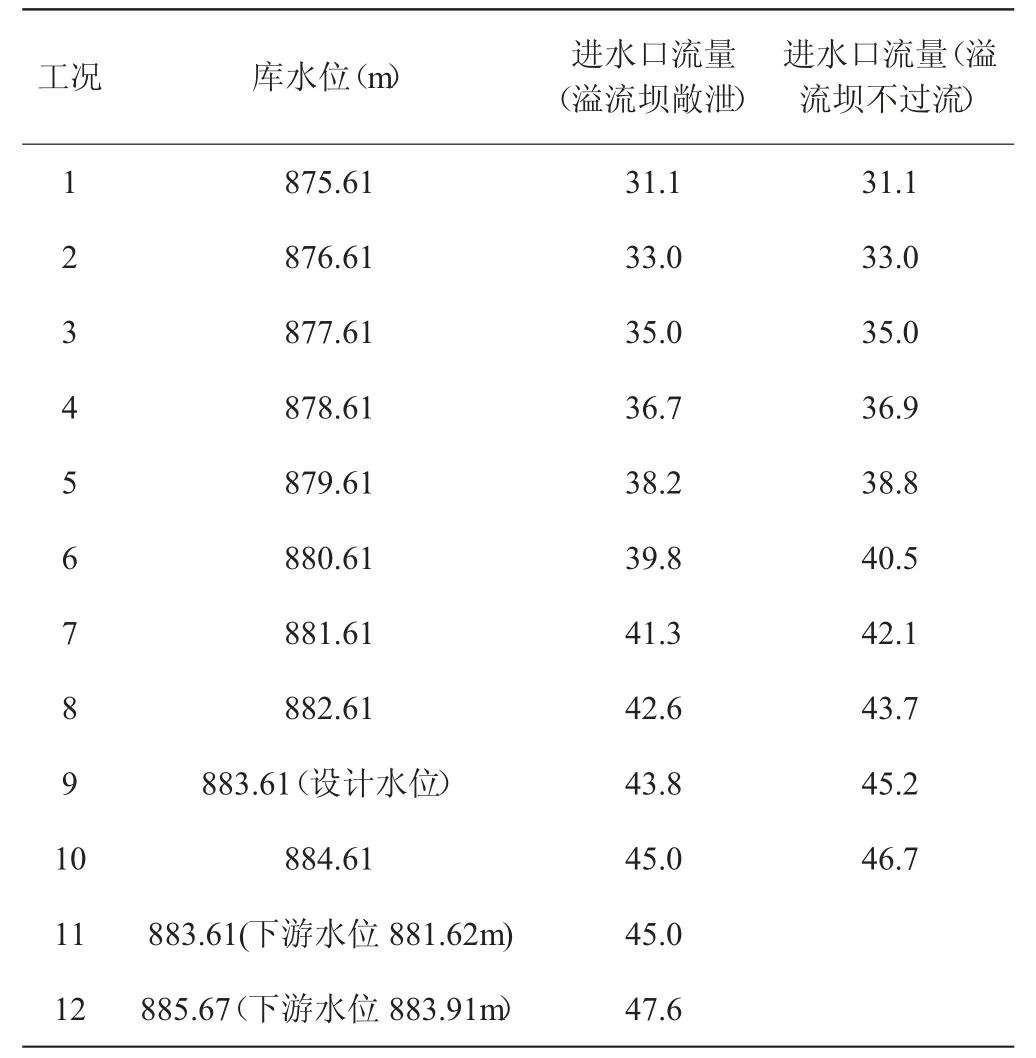
表1 不同库水位对应的进水口取水量 单位：m3/s

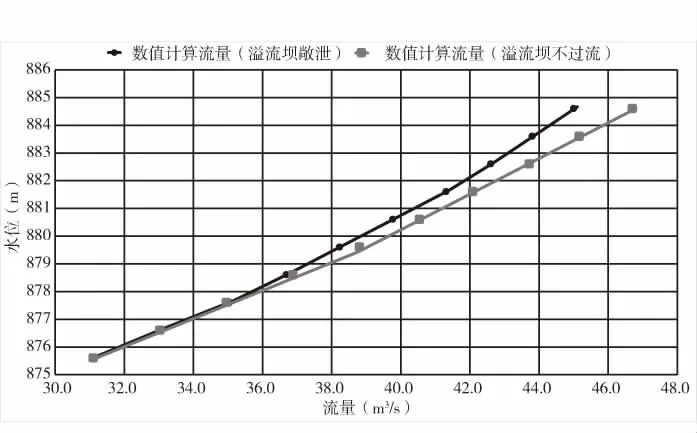
图3 水位- 流量关系曲线图

由图3、表1 可见，同一条件下，进水口取水流量随着库水位的增加而增大；同等水位条件下，溢流坝敞泄进水口取水量略小于溢流坝不过流情况，低水位时两者过流量基本一致，高水位时差异较大，最大差值在1 m3/s 左右（3%），表明溢流坝溢流对进水口取水量影响较小。上述结果均表明在保证正常蓄水位875.61 m，进水口取水流量达到31 m3/s 的条件下，随着上游水位的增加，进水口取水能力有所增大。现有布置条件下，进水口取水能力满足设计要求。

在正常蓄水位时（875.61 m），进水口段水流为有压流。水流进入进水口后受弯道影响，水流偏向右侧，进水口段流速在2.5 m/s 左右，水流从进水口段进入闸室段后向前冲击闸室壁后向下前方运动，出口压坡（收缩面积）后流速超过4 m/s。泄洪时，溢流坝下流速超过12 m/s，进水口的流速略大于库水位875.61 m 进水口流速。

图4 水库及进水口流速分布云图

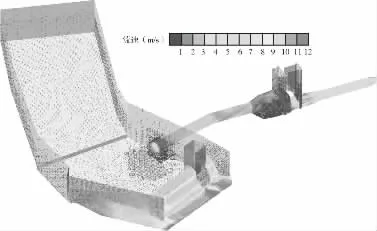
图5 水库及进水口流速分布矢量图

4 海里电站进水口水力学模型试验

4.1 试验内容及条件

通过模型试验研究确定模型出口压坡（收缩面积），通过试验研究得到不同水库水位时进水口的取水流量。根据模型试验现场条件，从正常蓄水位开始逐渐增加库水位，并测量进水口取水能力，当水库溢流坝泄流量及进水口取水量之和达到模型现场限制流量（原型不超过300 m3/s）后结束试验[2]。

4.2 模型试验成果

采用几何比尺为20 的模型进行试验。

图6 模型试验现场图

首先通过模型试验确定库水位875.61 m，进水口取水量31 m3/s 时的出口压坡（收缩面积），然后在固定出口压坡的情况下，通过试验研究得到不同水库水位时进水口的取水量，试验取水能力见表2。

表2 进水口取水流量

由表2 可见，在保证正常蓄水位875.61 m，进水口取水流量31 m3/s 的条件下，随着上游水位的增加，进水口取水流量有所增大，溢流坝泄流量迅速增大。表明现有布置条件下，不进水口取水能力满足设计要求。

正常蓄水位（875.61 m）时，进水口表面有一非贯穿性的浅表层旋涡存在，进水口段水流为有压流，随着库水位的逐渐增大，旋涡慢慢变小，该漩涡对进水口水力条件基本无影响。

4.3 试验成果与数值模拟计算成果对比分析

不同水位条件下，数值模拟计算进水口流量与模型试验流量对比见图7。由图7 可见，模型试验值与数值模拟值基本吻合，表明数值模拟得到的流量值较为准确。

图7 数值模拟流量与模型试验流量对比

5 结论

采用三维数值模拟及水力学模型试验技术对海里电站进水口取水能力进行研究。数值模拟结果表明：在库水位875.61 m，进水口及隧洞取水流量41.5 m3/s，满足取水能力设计要求。进水口局部三维数值模拟计算结果表明：溢流坝敞泄条件下，进水口取水量略小于溢流坝不过流情况，且低水位时两者基本一致，高水位时略有差异，最大差值在3%左右，表明溢流坝溢流对进水口的取水能力影响较小，同等条件下进水口取水量随着库水位的增加而增大。模型试验的结果也表明：进水口取水量随着库水位的增加而增大，模型试验与数值模拟结果基本吻合。

上述研究成果表明，现有进水口及隧洞布置条件下，进水口取水能力满足设计要求的31 m3/s，进水口取水量随着库水位的增加而增大，溢流坝溢流对进水口取水量影响很小。

通过数值模拟和模型试验论证，海里电站取水口取水能力满足设计要求，水力性态较为理想，取水比较安全。在合理的工程布局及措施下，径流式电站取水口布置于山区峡谷型陡坡急弯河段，是可行的，取水是安全的。