配筋混凝土轴向拉伸试验条件下的应力-应变关系研究

吴海林 朱良才 冉红洲 崔福冰 郑志强

(三峡大学 水利与环境学院， 湖北 宜昌 443002)

配筋混凝土轴向拉伸试验条件下的应力-应变关系研究

吴海林 朱良才 冉红洲 崔福冰 郑志强

(三峡大学 水利与环境学院， 湖北 宜昌 443002)

混凝土应力-应变关系是混凝土构件承载力、变形分析及裂缝研究的重要参数．本文设计制作了配筋混凝土试件开展配筋混凝土试件轴向拉伸试验，通过分离钢筋与混凝土分别承受的荷载，获得不同配筋率下的混凝土轴向拉伸应力-应变关系曲线，分段拟合得到对应的应力-应变曲线方程，并探讨了配筋率对混凝土轴向拉伸应力-应变关系曲线的影响规律．

钢筋混凝土； 轴向拉伸试验； 应力-应变全曲线； 数学模型

混凝土受力破坏过程中的应力-应变全曲线可以宏观地反映混凝土在各个受力阶段的变形、内部微裂缝的发展、损伤积累、最终破坏等一系列过程，同时又是分析和计算混凝土构件承载力和变形的重要参数．因此，混凝土应力-应变全曲线的研究对充分发挥材料强度、降低工程造价，更加合理地设计混凝土结构物具有十分重要的意义．目前，在钢筋混凝土结构的非线性分析中，少数研究者考虑了混凝土的软化特性(即应力-应变全曲线的下降段)[1-2]，而现有规范建议的软化曲线是针对素混凝土试件在承受简单轴向力的条件下获得的，适用于房屋和一般构筑物的钢筋混凝土、预应力混凝土以及素混凝土结构的设计[3]，而对于复杂的带缝工作配筋混凝土结构(如钢衬钢筋混凝土压力管道)的适用性还有待进一步研究．本文设计制作了配筋混凝土试件，开展配筋混凝土试件轴向拉伸试验，通过分离钢筋与混凝土分别承受的荷载，从而获得不同配筋率下的混凝土轴向拉伸应力-应变全曲线，拟合得到不同配筋率下的混凝土轴向拉伸应力-应变全曲线方程，并探讨了不同配筋率对混凝土轴向拉伸应力-应变全曲线的影响规律．

1 试验简介

1.1 试件设计及制作

轴向拉伸试验是测得配筋混凝土各项力学性能最为简单直观的方法，但试验中存在着偏心、应力集中、无固定断裂位置等诸多难点，影响试验的成功率及结果的准确性．本试验参考国内已开展的轴向拉伸试验成功案例及规范[4]，应用有限元法对试件体型及尺寸进行优化设计，确定轴向拉伸试件为外夹式哑铃型，变截面处采用圆弧平滑过渡，能够一定程度上改善以上问题[5]．本试验设计3组配筋混凝土试件，每组4个，选用混凝土强度等级为C25；各组受拉钢筋(HRB400，Ⅲ级钢筋)直径分别为10 mm、12 mm和14 mm，对应试件的配筋率为0.74%、1.12%和1.58%(分别对应P-1组、P-2组、P-3组试件)，为测取试件裂缝处钢筋应变，将钢筋沿轴线剖分，铣出一条2 mm×3 mm的浅槽．以每组试件测值的平均值作为试验结果，若一组试件中数据可用的试件少于两个，则重做该组试验．

图1 试件及钢筋三维示意图

1.2 试验及数据处理方法

试验采用具有10 t(100 kN)加载能力的电子万能试验机进行加载，采用位移控制加载，拉伸时的速率控制在0.01 mm/min．为保证试验过程中试件受力严格对中，设计和定做高精度的模具和夹具，并在试验正式开始前进行预拉，调整试件位置，参考规范[4]，将偏心率控制在15%以下．试验采用应变采集系统和荷载采集系统分离的方式采集轴向拉伸荷载、轴向拉伸过程中混凝土应变以及试件开裂处的钢筋应变等数据．参考文献[5]的数据处理方法，得到混凝土应力-应变全曲线．

英语专业学生的毕业论文是考查学生综合能力、评估学业成绩的重要方式。不同高校根据英语专业教学大纲的规定，结合本校的实际情况，制定出符合本校实际情况的要求。以北京师范大学珠海分校为例，英语专业的毕业论文要求用英语撰写，长度为6000单词左右，要求文字通顺、思路清晰、内容充实，有属于自己的创新点。论文评价除了考虑语言表达能力之外，主要把独立见解和创新意识作为重要依据。

2 配筋混凝土轴向拉伸试验结果分析

2.1 配筋混凝土试件应力-应变全曲线

本次试验P-1、P-2、P-3三组配筋混凝土试件分别测得2个、3个、3个试件的轴向拉伸试验数据可用．各试件所得混凝土轴向拉伸σ-ε曲线如图2～4所示．

图2 P-1组2个试件所得混凝土轴向拉伸σ - ε曲线

图3 P-2组3个试件所得混凝土轴向拉伸σ - ε曲线

图4 P-3组3个试件所得混凝土轴向拉伸σ - ε曲线

国内外已有混凝土轴向拉伸全曲线的方程形式为：单一函数型(分为多项式、指数式、有理分式)及分段函数型[7-8]．单一函数拟合混凝土轴向拉伸σ-ε曲线具有方程形式简单，便于运用中计算的特点．但其表达式无法体现混凝土轴向拉伸σ-ε关系的所有特征，因此，混凝土轴向拉伸σ-ε曲线采用分段函数进行拟合．结合混凝土轴向拉伸σ-ε曲线的上述特点，经综合比较，其上升段采用多项式形式拟合，下降段采用有理分式形式拟合．

国家要尽快制定一些相关的法律法规，为低碳经济的发展构建一个积极、完善、客观的外部环境，替低碳营销模式提供良好的氛围。现今，世界各国都在相继制定、出台与低碳经济相关的法律、法规。例如美国制定的《低碳经济法案》、英国出台的《可再生能源义务》、丹麦的绿色能源的发展模式和意大利的“白色证书”“绿色证书”、能源计划等等。我国也应该着手这方面立法的研究。在制定相关的法律法规时，添加应对气候变化的相关条款，在规划、批报项目和战略环评的规则中增加气候影响评价的规定，逐渐建立健全应对气候变化的体系。

广东省各级政府加强调查研究，积极借鉴有关地方的成功经验，结合自身实际情况，在加大财政投入方面取得明显成效。如全省21个地级以上市均出台了加快水利改革发展的政策文件，明确从土地出让收益提取10%用于农田水利建设、从城市维护税中划出15%用于城市防洪排涝和水资源工程建设等。广州、深圳、东莞由财政一次性解决城乡水利防灾减灾工程建设资金，中山市规定市、镇两级财政投入水利工程建设的资金，每年以10%的增幅递增等。

确保保险公司财务目标的顺利实现，必须对保险公司财务计划的执行过程进行相应的监督和调节。这就需要保险公司强化内部财务控制，充分考虑影响保险公司财务管理活动的各项影响因素，有针对性的制定保险公司财务风险管理措施，确保保险公司财务目标的顺利实现。

图5 3组配筋混凝土试件所得平均轴向拉伸σ - ε曲线

2.2 配筋混凝土试件峰值应力及峰值应变

在配筋混凝土试件轴向拉伸σ-ε曲线的基础上，分析比较各试件所得曲线的特征点，研究配筋率与混凝土峰值应力、峰值拉应变等特征参数的关系．所有配筋混凝土试件的峰值应力、峰值拉应变统计情况见表1．

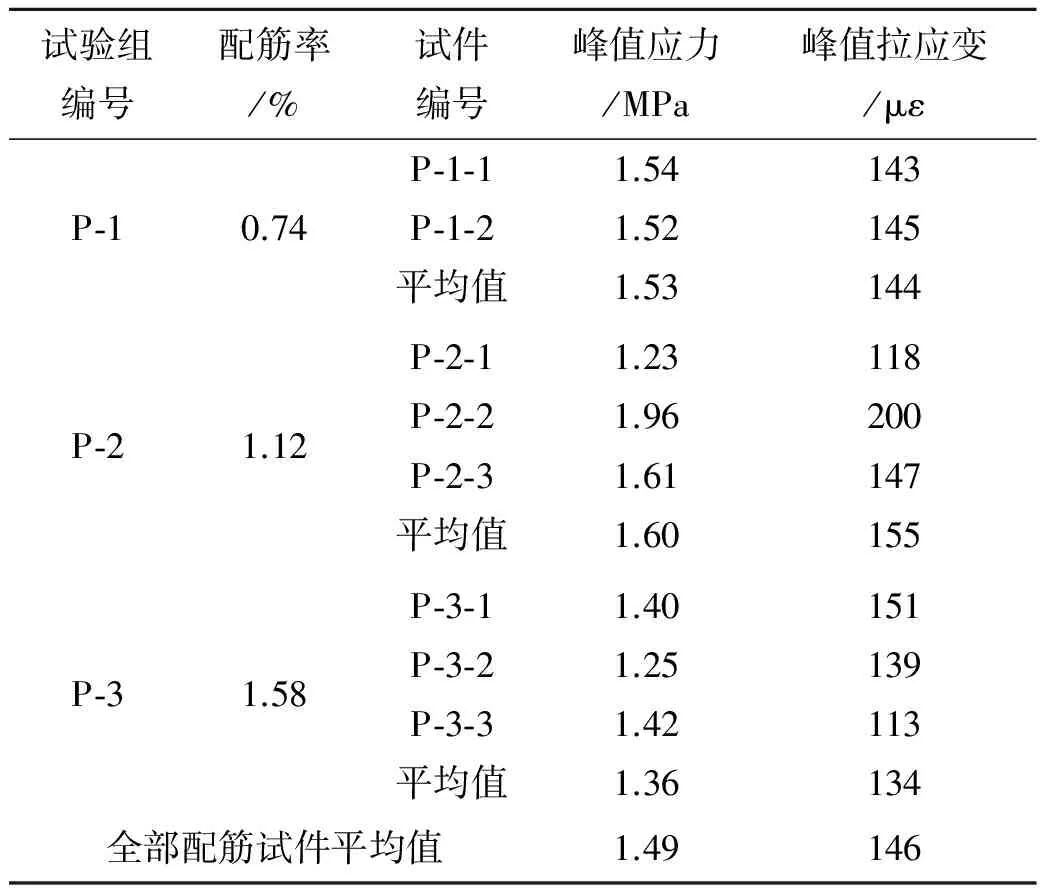
表1 配筋混凝土试件所得混凝土峰值应力及峰值拉应变

由表1可知，3组配筋混凝土试件所得的混凝土峰值应力平均值分别为1.53 MPa、1.60 MPa和1.36 MPa，峰值应力的变化与配筋率的变化并无明显的规律．ρ=1.12%时，最大峰值应力为1.96 MPa，最小为1.23 MPa，相差0.73 MPa，波动幅度较大；ρ=1.58%时，最大峰值应力为1.42 MPa，最小为1.25 MPa，相差0.17 MPa，波动幅度也相对较大．说明同组试验内，各试件的峰值应力可能也具有较大的离散性．

3组配筋混凝土试件的平均峰值拉应变分别为144×10-6、155×10-6和134×10-6，峰值拉应变与配筋率的变化也没有显示出明显的规律性．但是，峰值拉应变随峰值应力的改变呈现一定规律：峰值拉应变随峰值应力的增大而增大，随其减小而减小．

3 混凝土轴向拉伸应力-应变全曲线数学模型研究

3.1 混凝土轴向拉伸应力-应变全曲线数学模型型式选取

图6 实测平均轴向拉伸σ - ε曲线

由图2～4可知，配筋混凝土轴向拉伸σ-ε曲线的上升段中应力、应变基本呈线性关系，在接近峰值应力时，试件的应变发展较快，应力增长较慢．曲线达到峰值后，有一个应力减小较快、应变增加较慢的短暂过程，接着应力减小速率降低，应变增加速率加快，最后曲线趋于平缓．

3.2 应力-应变全曲线上升段拟合方程

如图6所示，3条曲线的上升段近似重合，故用统一表达式对3条曲线上升段进行拟合．参考规范[6]，本文表达式采用与之类似的多项式：

如图5所示，为3组配筋混凝土试件轴向拉伸试验所得的混凝土平均轴向拉伸σ-ε曲线．3组配筋试件轴向拉伸试验得到的σ-ε曲线的上升段较为相似，但峰值应力离散性较大．同时，峰值应力之后、曲线趋于平缓之前，此段线型随着配筋率变小而变陡，而曲线的平缓阶段差别较小，即各组试件的残余应力大小与配筋率之间的关系未呈现出明显规律．

1.2 观察指标 通过院内病案查询系统采集患者的临床资料：(1)临床基本情况，包括年龄、性别、从DM/PM确诊到出现ARDS的病程、ARDS诱因、预后；(2)症状和体征，包括肺内(咳嗽、咳痰、呼吸困难)及肺外(发热、关节肌肉痛、特征性皮疹)表现；(3)辅助检查结果，包括血常规、血沉、血生化、抗体、血气分析，影像学，肌电图，肌肉活检，支气管镜肺活检结果等；(4)DM/PM治疗及针对ARDS的激素使用情况。

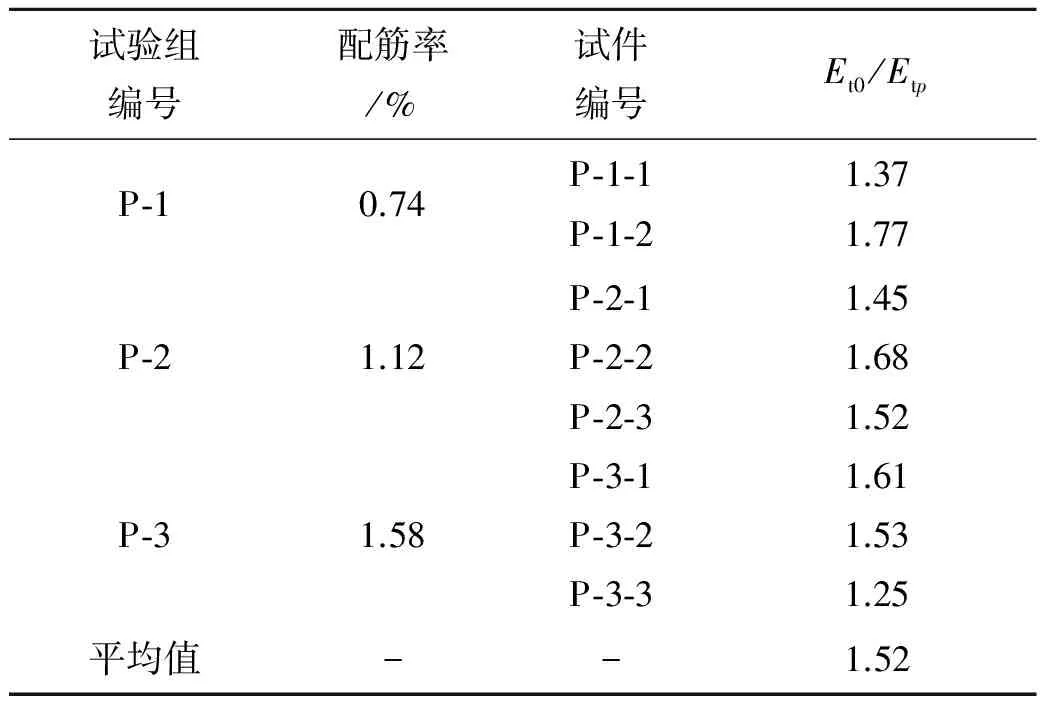
表2 配筋混凝土试件轴向拉伸主要试验结果

在曲线拟合过程中，首先通过试算确定α值，使得拟合曲线下降段与实测曲线接近，各组试件所得曲线中α值试算结果如图8所示．其次结合实测值和式5计算β值，采用最小二乘法计算试验数据确定另一参数β值．

图7 实测上升段平均曲线及其拟合曲线

采用相关指数R描述非线性方程与实测数据间拟合程度．

根据方程3，得出上升段的拟合曲线，并与试验所测上升段平均曲线对比，如图7所示．

R的范围一般为0≤R≤1，R越小，表明曲线与实测数据拟合越差，反之，R越大，则曲线与实测数据拟合越好．采用图7中的实测值和拟合值计算得出R=0.968，拟合曲线与实测曲线吻合良好，此曲线上升段的拟合方程较为合理，可在一定程度上表达出基于配筋混凝土轴向拉伸试验所测得混凝土轴向拉伸σ-ε曲线的上升段．

本组患者实施阿卡波糖(批准文号:国药准字H20020202,2010-01-18;生产单位为杭州中美华东制药有限公司)治疗,具体措施:用药第1-3天使用剂量为50mg,用药第四天使用剂量为100mg,每日3次[3]。

3.3 应力-应变全曲线下降段拟合方程

式中，α、β控制曲线的重要参数．经分析可知曲线下降段的陡缓对参数α较敏感，曲线平缓段对参数β更敏感．

反射光分布测量装置如图2所示[9]。激光辐照在样品表面，通过改变激光入射方向入射角度，利用半圆阵列分布的光电探测器收集散射光，实现各路信号的光电转换，利用数据采集记录探测阵列的输出信号。利用所设计的实验装置，对不同材料粗糙表面、不同入射角度粗糙表面及同一材料不同表面粗糙度的BRDF特性开展了实验测试，测试的散射光强分布用归一化值进行表征[10]。

参考规范[6]，混凝土轴向拉伸σ-ε曲线下降段的方程为：

图8 各组试件所得曲线下降段α值试算结果

由表2可知，试验测得系数a的值在1.25～1.77之间波动，取3组试件平均值的近似值1.5作为a值．由此可进一步得到曲线上升段方程为：

由图8可知，β为0.74%、1.12%和1.58%的3组试件，α分别取1.8、0.7和0.4时，拟合曲线下降段与各条曲线下降段拟合较好．分别计算出各曲线的β值，最终结果见表3，通过计算得出下降段P-1、P-2、P-3的相关指数R值分别为0.981、0.995、0.974，表明3组试件的下降段拟合曲线与实测曲线吻合良好．

表3 不同曲线拟合方程的参数取值

综上，本文配筋混凝土试件轴向拉伸试验所得3种不同配筋率对应的混凝土轴向拉伸σ-ε曲线可以采用以下表达式描述：

其中，α和β按表3取值．由此可得到每组试件所得混凝土轴向拉伸σ-ε关系的拟合曲线，与实测曲线的对比如图9所示．可以发现，3组曲线的拟合都取得了较好的效果．

图9 配筋混凝土试件所得实测及拟合σ - ε曲线

图10为3种配筋率混凝土试件所得拟合σ-ε曲线对比图．由图可知，几条曲线上升段近似重合，主要区别出现在下降段．对于3条曲线达到峰值后、趋于平缓之前的下降段，试件的配筋率越大，下降段越缓，在拟合方程中体现为参数α值越小．3条曲线的平缓段与配筋率无明显规律，在拟合方程上体现为参数β值不随试件配筋率的变化而呈规律性变化．

参观过程中我们了解到，某一期海外学员培训，学员悄悄向授课老师索要印有科雷logo的T恤，“我们深入了解后才知道，在他们眼里，这在国外印刷行业是一种身份的象征，并以之为荣，而且当地客户认这个品牌”。此后，科雷logo T恤也成为学员们的一个标配。

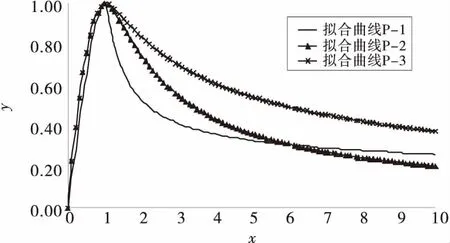
图10 拟合σ - ε曲线

4 结 论

本文开展配筋混凝土试件轴向拉伸试验，分离钢筋与混凝土分别承受的荷载，获得不同配筋率下的混凝土轴向拉伸应力-应变全曲线，拟合应力-应变全曲线方程，探讨不同配筋率对混凝土轴向拉伸应力-应变全曲线的影响规律．得到以下主要结论：

1)混凝土应力-应变全曲线随配筋率的变化规律：3条曲线的上升段几乎重合，可以得出不同配筋率对应力-应变曲线上升段的影响较小；在峰值应力之后、曲线趋于平缓之前，试件配筋率越小，曲线越陡；在曲线平缓段，各曲线差别较小，即不同配筋率对混凝土残余应力的大小无明显影响规律．混凝土峰值拉应力及峰值拉应变与配筋率未呈现规律性变化，但峰值拉应变随峰值应力的增大而增大、随峰值应力的减小而减小．

2)采用分段函数对各组试件的应力-应变全曲线进行拟合，分别得到应力-应变全曲线上升段和下降段的数学模型，拟合曲线与实测曲线吻合良好．配筋率对拟合曲线的影响主要表现在曲线的下降段，在拟合方程上体现为配筋率越大，参数α值越小，下降段越缓；不同配筋率对拟合曲线的平缓段无明显影响规律，在拟合方程上体现为参数β值不随试件配筋率的变化而呈规律性变化．

[1] 申 艳，叶 锐．混凝土受拉软化特性对完全联合承载蜗壳非线性有限元分析的影响研究[J]．中国农村水利水电．2011(5)：97-100．

[2] 张运良，张存慧，马震岳．三峡水电站直埋式蜗壳结构的非线性分析[J]．水利学报，2009，E40(2)：220-225．

[3] 过镇海，张秀琴．砼应力-应变全曲线的试验研究[J]．建筑结构学报，1988,9(4)：45-53．

[4] SL 352-2006．水工混凝土试验规程[S]．北京：中国水利水电出版社,2006．

[5] 吴海林，冉红洲，吴 龙．配筋混凝土轴拉试验方法及装置研究[J]．科学技术与工程，2015，15(2)：275-278．

[6] GB50010-2010．混凝土结构设计规范[S]．北京：中国建筑工业出版社,2010．

[7] 江见鲸，陆新征．混凝土结构有限元分析[M]．北京：清华大学出版社,2003．

[8] 陈 萍，梁正平，黄书秦，等．三峡三级配混凝土轴向拉伸应力-变形全曲线[J]．河海大学学报，2001，29(5)：38-41．

StudyofStress-strainRelationshipofReinforcedConcreteunderAxialTensileTest

Wu Hailin Zhu Liangcai Ran Hongzhou Cui Fubing Zheng Zhiqiang

(College of Hydraulic & Environmental, China Three Gorges Univ.，Yichang 443002， China)

Concrete stress-strain curve is an important parameter of concrete component bearing capacity, deformation analysis and crack research.In this paper, reinforced concrete specimens were designed and produced to carry out the tensile test of reinforced concrete specimens, so as to get the concrete axial tensile complete Stress-Strain curve in different reinforcement ratios by separating loads between steel and concrete, the axial tensile stress-strain curves of concrete under different reinforcement ratios, and then the corresponding stress - strain curve equation is obtained by piecewise fitting. Meanwhile, the influence of reinforcement ratio on axial tensile stress - strain curve of concrete is discussed.

reinforced concrete; axial tensile test; complete stress - strain curve; mathematical model

10.13393/j.cnki.issn.1672-948X.2017.05.010

2017-05-09

国家自然科学基金项目(51379107)

吴海林(1977-)，男，教授，博士，主要从事水工结构数值模拟与模型试验研究．E-mail：82667105@qq.com

TU502+.6

A

1672-948X(2017)05-0048-05

[责任编辑周文凯]