两种线性地球自转参数短期预报方法

郭忠臣, 徐 波

(1. 宿州学院 环境与测绘工程学院, 安徽 宿州 234000; 2. 河南省测绘工程院, 河南 郑州 450003)

两种线性地球自转参数短期预报方法

郭忠臣1, 徐 波2

(1. 宿州学院 环境与测绘工程学院, 安徽 宿州 234000; 2. 河南省测绘工程院, 河南 郑州 450003)

介绍了两种常用线性地球自转参数短期预报的原理和方法,处理了地球自转参数相关数据,并进行了分析.

地球自转参数; 最小二乘; ARMA; 定阶

地球自转参数(ERP)在高精度卫星导航、深空探测等领域具有不可替代的作用,对其实时性的要求也越来越高[1-2].当前高精度ERP的观测手段主要有VLBI、SLR、GNSS等,但这些方法并不能实时地给出ERP,根据测定技术的不同,往往都需要延迟几个小时至数天,而且观测的精度也不甚相同,如GNSS技术虽然解算速度较SLR、VLBI等技术快,但是其解算结果有时还需VLBI和SLR技术的解算值来进行修正[2-4],因此想要实时测定高精度的ERP目前并不可行.基于此,高精度的ERP预测技术就显得尤为重要,但因ERP受到众多可测及不可测的激发源的影响,导致其预报工作较为困难.因此,构建一种较为合理、有效的高精度预报模型也成为了当下大地测量工作者的主要任务之一[5].本文对当前主要使用的预报方法原理进行分析,并依据ERP相关性质,构造出相应的预报模型,以供后续研究使用.

1 ERP短期预报方法

为推进地球自转参数预测的研究,IERS于2005年10月1日—2008年2月28日组织了地球自转参数预测方案比较大会战(earth orientation parameters prediction comparison campaign, EOP PCC)来确定EOP预测的现状,活动在两年半的时间内收到了11位参与人员的近6500份预报值,采用的预报方法主要有:最小二乘外推法和自回归模型(lst squares extrapolation of the harmonic model and autoregressive prediction)、谱分析和最小二乘外推法(sectral analysis and least squares extrapolation)、卡尔曼滤波法(Kalman filter)、神经网络模型(nural networks)、联合大气角动量预报(ading AAM in LOD prediction)、小波分解和自协方差预测(wvelet decomposition an auto-ovariance prediction)等方法[6-7].此次活动得出:不同方法组合的预报精度优于单一方法,没有一种预报方法既适合所有跨度又适合EOP所有参数.国内外学者一致认为,在极移预报方面:LS+AR模型、频谱分析与最小二乘方法及神经网络较优于其他方法;在UT1-TC/LOD方面,小波分析和自协方差、卡尔曼滤波、联合AAM预报优于其他预报方法.

当前对ERP进行预报的主要方法可分为线性方法和非线性方法,本文主要对两种常用线性方法的预报原理进行介绍.

2 最小二乘外推法

最小二乘法是通过最小化误差的平方和寻找数据的最佳函数匹配,利用最小二乘法可以简单地求出未知参数[8].早期对ERP进行预测时,多采用最小二乘法对ERP的趋势项和周期项进行拟合,并通过拟合参数对ERP外推预报.

最小二乘法的一般模型可表示为[9-10]:

式中:L为观测向量;B为观测矩阵.

将式(1)转换成误差方程即:

式中:i=1,2,…,n,令

则式(2)可化为

根据最小二乘原理

式(4)可表达为

通过式(5)即可求得:

由文献[8]可知,极移受长期趋势项和周期项(Chandler项、周年项)的影响比较大,因此,根据最小二乘原理,在只考虑趋势项和周期项的条件下可构造极移PMX和PMY的最小二乘模型如下:

式中ai、bi为趋势项的拟合系数,ci、di为各周期项的振幅,P1、P2分别为周年项和Chandler项的周期,ωi为各周期项的相位,t为时间.

与极移类似,LODR也主要受到长期趋势项和周期项(周年项、半周年项)的影响,可构造其最小二乘模型如下:

式中a、b为趋势项的拟合系数;c、d为各周期项的振幅;P1、P2分别为周年项和半周年项的周期;ωi为各周期项的相位;t为时间.

图1为用最小二乘方法对2005年1月1日—2015年1月1日(MJD:53371-57023)期间的地球自转参数(PMX、PMY和LODR)的拟合结果.

图1 地球自转参数拟合结果Fig.1 The fitting result of ERP(a)—PMX; (b)—PMY; (c)—LODR.

最小二乘法只能对ERP中的周期项和趋势项等主项进行外推预报,由于该模型并不能将各影响因素完整的反映出来,所以通过该式拟合后会得到一组残差序列,该残差序列包含了其他较小因素的影响程度,需通过其他模型对该残差项进行处理预报.

3 ARMA模型

3.1 模型简介

对包含测量随机噪声以及不甚明显的周期性变化的时间序列进行分析,并建立其数学模型的方法和过程称为时间序列分析,简称时序分析[11-12].时间序列分析的ARMA模型就是对平稳时间序列Zt(t=1,2,…,n)建立理想的统计模型,其数学模型表示为[13]

式(9)被称为p阶自回归,q阶滑动平均的时间序列模型,简记为ARMA(p,q),其中:φ1,φ2,…,φp为模型的自回归系数,θ1,θ2,…,θq为模型的滑动平均系数,at为t=t,t-1,…,t-q时刻的白噪声序列.

由式(9)可知,zt主要受序列内部规律和白噪声的影响,即式(9)可表示为

若zt仅与t时刻的白噪声以及之前的规律性有关,则式(10)可表示为

此时,称式(11)为p阶自回归模型,记为ARMA(p,0)或者AR(p).

若zt仅与t时刻以及之前的白噪声有关,此时式(10)可表示为

这时,称式(12)为q阶滑动平均模型,记为ARMA(0,q)或者MA(q).

假设一时间序列zt(t=1,2,…,n)为AR(p)模型,即有

令t=n+1,即可根据式(13)得到zn+1时刻的状态:

3.2 模型识别

使用ARMA模型对时间序列进行分析时,需选择与该序列契合度较高的模型,通常根据时间序列的自/偏自相关函数的性质来判断.

设有平稳时间序列Zt(t=1,2,…,n),其自/偏自相关函数计算公式如下:

通过证明可知,平稳时间序列的相关函数存在“截尾”和“拖尾”的特性.“截尾”是指当k大于某个值时,相关函数全部为“零”,“拖尾”是指当k大于某个值时,相关函数趋近于“零”,但不会恒等于“零”.时间序列相关函数的“截尾”和“拖尾”现象,为模型选择提供了依据,表1为模型选择原则.

表1 平稳时间序列ARMA模型识别原则

根据表1中模型识别原则,分别求出ERP各项残差序列的自/偏自相关函数,通过分析其“截尾”“拖尾”特性即可判断使用何种模型.因两个极移方向的变化相同,LOD与UT1-UTC又可互相转化得到,因此本文只对PMX和LOD残差序列的相关函数进行分析.通过图2和图3可以看出,PMX和LOD的自相关函数均存在“拖尾”现象,偏自相关函数均存在“截尾”现象,依据表1中模型判别原则,即可知PMX、LOD的残差序列均适用于AR模型,又因PMY和UT1-UTC分别与PMX和LOD类似,所以PMY、UT1-UTC的残差序列也均适用于AR模型.

图2 PMX残差序列相关函数图Fig.2 The correlation function figure of PMX residual

图3 LOD残差序列相关函数图Fig.3 The correlation function figure of LOD residual

3.3 模型定阶

确定模型类别之后还需确定模型阶数,通常情况下,模型阶数越高,拟合精度越好,但随着阶数的增加,需要的信息也随之增多,当信息量不变的情况下,阶数过多反而会导致拟合误差变大,而阶数过少,预测结果会容易受到观测粗差的影响,因此需要一种合理的方法来确定模型阶数[12].常用的AR模型定阶准则有信息论准则(AIC)、传递函数准则(CAT)和最终预测误差准则(FPE),在使用时,这三个准则是等效的,本文主要介绍AIC准则来确定AR模型阶数p.

AIC准则由赤池弘次于1973年提出,其一般形式为

对于AR模型,假设其阶数为k,AIC准则可表示为

根据AIC准则判定AR模型最优阶数时首先需合理的确定阶数上限p(p≪n),理论上当AIC(k)取最小值时,阶数k即为最佳阶数,但因该准则只是模型优化的一种宏观度量,并不能单纯的以AIC(k)最小来确定阶数,根据分析,当阶数大于一定值后,AIC(p)的变化幅度较小.选取一组数据进行试验,考虑到基础时间序列的长度以及AIC(p)的变化情况,本次试验取阶数上限为30,当序列长度或跨度时间不同时,模型最优阶数的选取可能不同,随机选取多种情况中的一种,分别计算不同阶数对应的AIC值.通过图4可知,当阶数为28时,此时AIC值最小,但当阶数大于8时,AIC值的变化趋于平缓,故在确定AR模型阶数时,可根据基础序列的长度以及计算时间效率等方面综合考虑,以取得较优的阶数.

图4 AIC准则Fig.4 AIC criterion

假设有零均值平稳时间序列Zt(t=1,2,…,n),确定其最佳阶数为p,则该时间序列可表示为

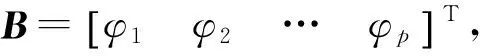
此时有

即

又可表示为

式(21)用矩阵表示为

4 结 语

当前有多种空间大地测量技术可精确测定ERP,但由于数据处理过程复杂,并不能实时得到高精度的ERP测定结果.考虑到ERP在现代空间导航中的作用日渐显著,高精度ERP预报方法也成为了当今亟待解决的问题之一.本文主要对两种常用线性预报方法的原理进行介绍,并通过实验对其在ERP预报中的可行性进行分析,也为后续使用该方法进行预报提供基础.

[ 1 ] WANG Q X,DANG Y M,XU TI H. The method of earth rotation parameter determination using GNSS observations and precision analysis[C]∥Lecture Notes in Electrical Engineering. Berlin: Springer, 2013:247-256.

[ 2 ] YAO Y B,YUE S Q,PENG C. A new LS+AR model with additional error correction for polar motion forecast[J]. Science China Earth Science, 2013,56(5):818-828.

[ 3 ] 魏二虎,常亮,刘经南. 我国进行激光测月的研究[J]. 测绘信息与工程, 2006,31(3):1-3.

WEI E H,CHANG L,LIU J N. Research on the lunar laser ranging for China[J]. Journal of Geomatics, 2006,31(3).

[ 4 ] 张志斌,王广利,刘祥,等. 中国VLBI网观测地球定向参数能力分析[J]. 武汉大学学报(信息科学版), 2013,38(8):911-915.

ZHANG Z B,WANG G L,LIU X,et al. Analysis of EOPdetermination via Chinese VLBI network[J]. Geomatics amp; Information Science of Wuhan University, 2013,38(8):911-915.

[ 5 ] 王潜心. 基于GNSS观测数据的高精度地球自转参数测定理论与方法研究[D]. 西安:西安测绘研究所, 2015.

WANG Q X. The theory and method of earth rotation parameters determination using GNSS observation data[D]. Xi’an: Xi’an Institute of Surveying and mapping, 2015.

[ 6 ] KALARUS M,SCHUH H,KOSEK W,et al. Achievements of the earth orientation parameters prediction comparison campaign[J]. Journal of Geodesy, 2010,84(10):587-596.

[ 7 ] XU X Q,ZHOU Y H . EOP prediction using least square fitting and autoregressive filter over optimized data intervals[J]. Advances in Space Research, 2015,56(10):2248-2253.

[ 8 ] 贾小勇,徐传胜,白欣. 最小二乘法的创立及其思想方法[J]. 西北大学学报(自然科学版), 2006,36(3):507-511.

JIA X Y,XU C S,BAI X. The invention and way of thinking on least sqeares[J]. Jounnal of Northwest University (Natural Science Edition), 2006,36(3):507-511.

[ 9 ] XU X Q,ZHOU Y H. EOP prediction using least square fitting and autoregressive filter over optimized data intervals[J]. Advances in Space Research, 2015,56(10):2248-2253.

[10] XU X Q,ZHOU Y H,LIAO X H. Short-term earth orientation parameters predictions by combination of the least-squares, AR model and Kalman filter[J]. Journal of Geodynamics, 2012,62(8):83-86.

[11] 武伟,刘希玉,杨怡,等. 时间序列分析方法及ARMA,GARCH两种常用模型[J]. 计算机技术与发展, 2010,20(1):247-249.

WU W,LIU X Y,YANG Y,et al. Analysis method of time array and two mosels of ARMA and GARCH[J]. Computer Technology and Development, 2010,20(1):247-249.

[12] 陈晓锋. AIC准则及其在计量经济学中的应用研究[D]. 天津:天津财经大学, 2012.

CHEN X F. Akaike information criterion and its application in econometrics[D]. Tianjin: Tianjin University of Finance amp; Economics, 2012.

[13] 刘海洋,郝哲. 基于时序分析的边坡变形预报与变形行为特征[J]. 沈阳大学学报(自然科学版), 2012,24(2):81-86.

LIU H Y,HAO Z. Prediction and behavior characteristic resarach of slope deformation based on time series analysis[J]. Journal of Shenyang University(Natutral Science), 2012,24(2):81-86.

【责任编辑:肖景魁】

TwoLinearShort-TermPredictionMethodsofEarthRotationParaments

GuoZhongchen1,XuBo2

(1. Faculty of Environment Science and Surveying Engineering, Suzhou University, Suzhou 234000, China; 2. Henan Surveying and Mapping Engineering Institute, Zhengzhou 450003, China)

The principle of two short-time forecasting method of linear earth rotation parameters was introduced, and the data of the Earth’s rotation parameter was analyzed.

earth rotation parameters; least square; ARMA; order

P 228.6

A

2017-09-25

郭忠臣(1992-),男,安徽阜阳人,宿州学院助教.

2095-5456(2017)06-0505-06