逆变器复合控制方案稳定性准确性和快速性的判定方法研究

2017-12-14崔睿

船电技术 2017年11期

崔睿

崔睿

（武汉第二船舶设计研究所，武汉 430064）

本文针对重复控制加PI控制的复合控制方案，参照重复控制稳定性、准确性和快速性的判定方法总结出适用于复合控制方案的判定方法。并将重复控制器与复合控制方案的特性进行了对比，从理论上说明了判据的有效性。最后通过仿真进一步验证复合控制方案的判定方法。

逆变器重复控制复合控制方案

0 引言

逆变器在交流稳定电源的应用中，波形控制技术一直是研究的热点之一。

文献[1]使用瞬时值反馈控制与重复控制组成的复合控制方案，重复控制抑制谐波，瞬时值反馈控制加快动态响应速度。文献[2]将重复控制和无差拍控制相结合可使系统具有输出波形好，动态响应快，适应负载的能力强等优点。文献[3]基于内模原理，利用传统PI控制与重复控制相结合的复合控制方案达到输出电压波形控制的目的。在众多复合控制方案中，重复控制加PI控制的复合控制方案实施起来较为容易，工程上应用广泛。

在众多文献中都提到了重复控制加PI控制的结合，应用在逆变器中，利用重复控制抑制谐波，挺高波形质量，利用PI控制加快响应速度，同时消除基波稳态误差。在设计重复控制器与PI控制器时，都是分开设计的。当分别控制都稳定，且特性满足控制要求时，直接并联在一起，进行控制。那么很自然的会有如下几个问题，是不是重复控制器与PI控制器单独控制时稳定，并联起来系统就一定稳定呢？还有，两种控制器并联以后，除了从仿真结果与实验结果来证明控制特性的改善，有没有什么类似于对重复控制器进行判定的标准，对重复加PI这种复合控制方案进行考察呢？为此，本文针对重复控制加PI控制的复合控制方案，总结了复合控制方案的判定方法，对于复合控制器的设计具有重要的指导意义。

1 重复控制原理及判定标准

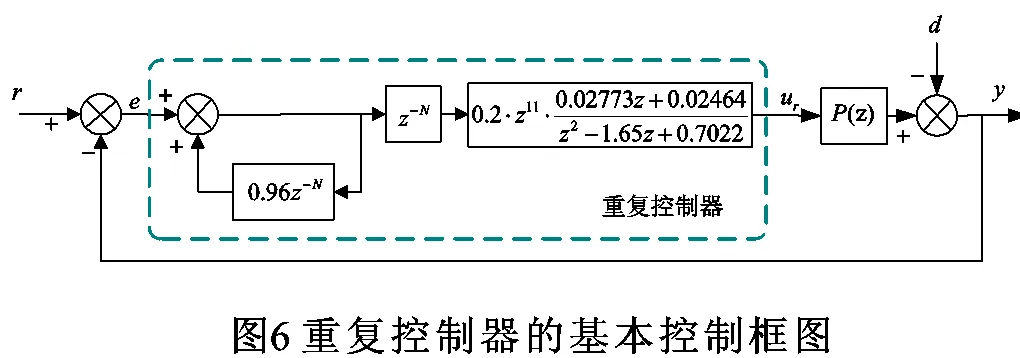
重复控制器一般由三部分组成：重复信号发生器内模、周期延迟环节和补偿器。重复控制器的基本控制框图如图1所示。

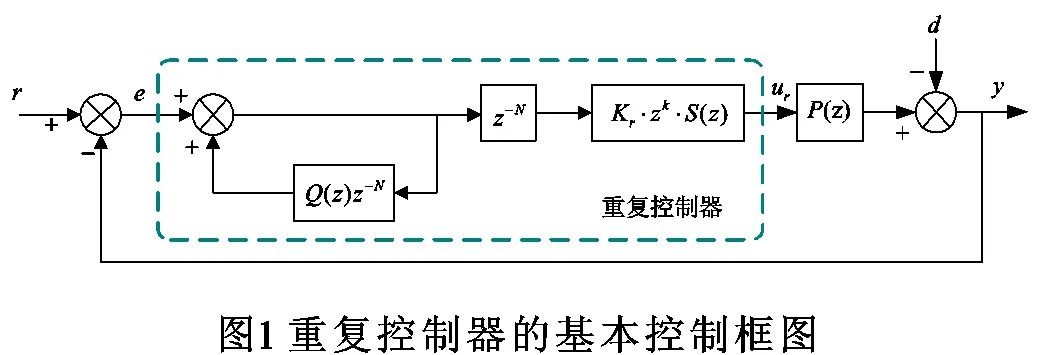
1）重复信号发生器内模：重复信号发生器内模是重复控制的灵魂所在，其基本思想源于控制理论中的内模原理，它是对误差进行以周期为步长的累加2)周期延迟环节z-N的作用是使控制动作延迟一个基波周期进行，是为了达到等效超前控制的目的。3)补偿器Kr·zk·S(z)是重复控制器设计中最为重要的环节，是针对控制对象P(z)的频率特而设置的。文献[4]中推导了重复控制稳定性、准确性和快速性的判定方法如下表所示。

2 复合控制方案的判定方法

参考文献[4]中推导了重复控制稳定性、准确性和快速性的判定方法，推导复合控制方案的判定标准。

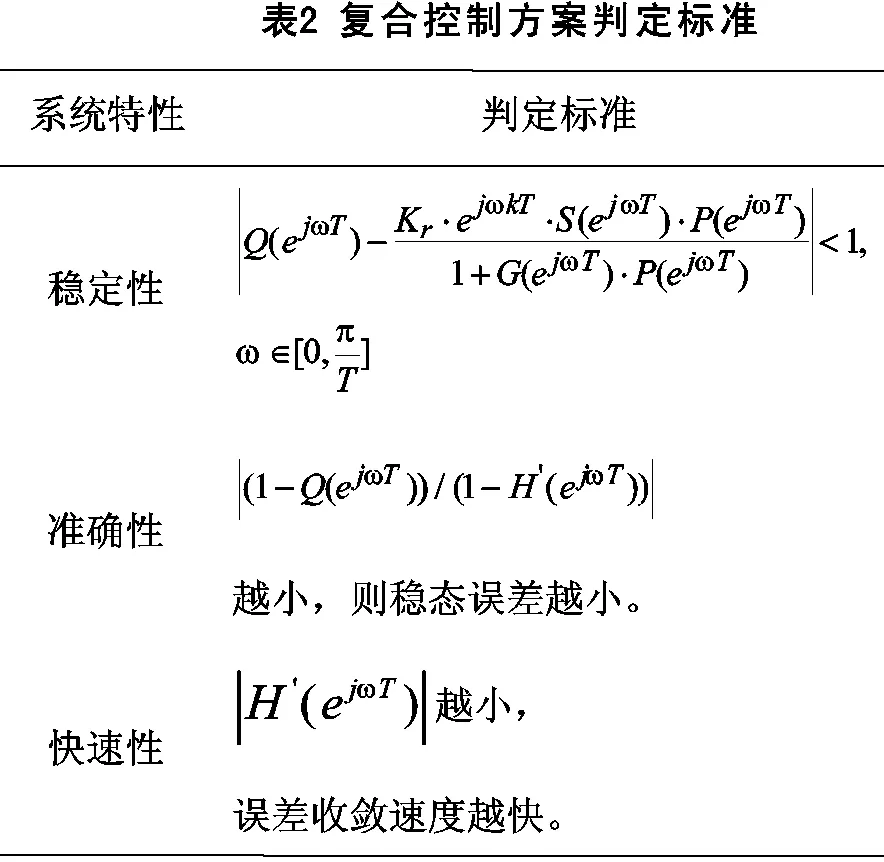
1)稳定性

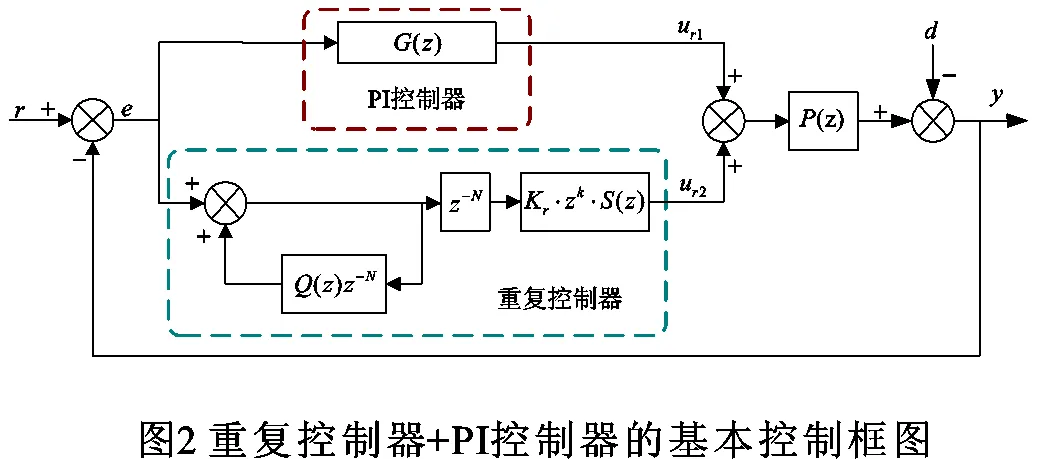
重复控制器加上PI控制器后的控制框图如图2所示，其中r为控制指令，y为控制对象输出，P(z)为控制对象，d为负载扰动，虚线框内为控制器。由图2不难得到：

进一步得到误差()表达式为

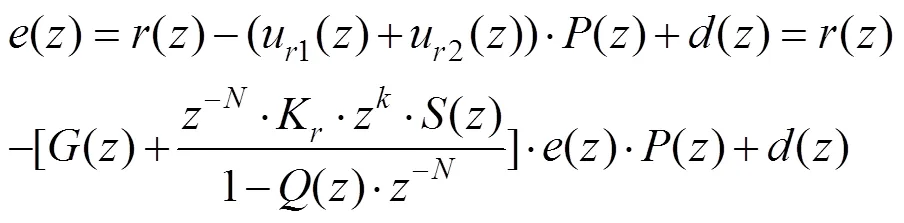
式(2)整理后得:

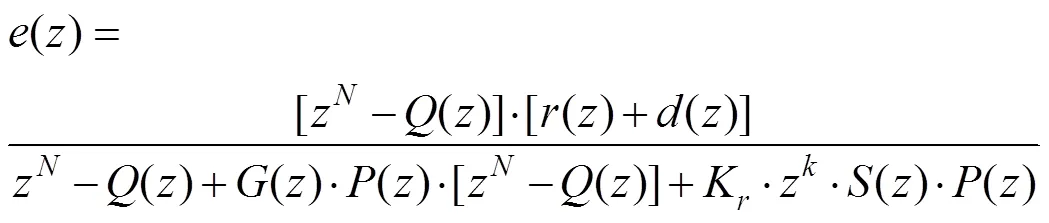
系统的特征方程为

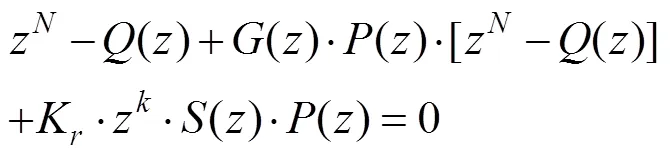
将系统特征方程变形如下

①若1+()·()=0

那么系统的特征方程可以化简为z·()·()=0，特性根即为下面方程组的解

可以用MATLAB画出1+()·()和z·()·()的零极点图，看两者有没有一样的零点，即看上面的方程组有没有解，如图3、图4所示（其中圆圈代表零点，叉代表极点）。

从图3、图4很容易看出，1+()·()和z·()·()没有相同的零点，即方程1+()·()=0的根不是系统的特征根，特征方程两边可以同时除以1+()·()来化简。②1+()·()≠0

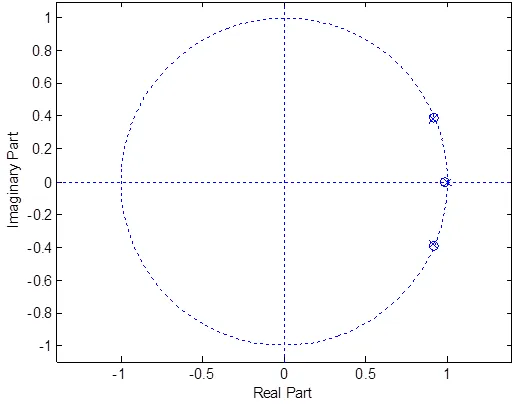
图3 1+G(z)·P(z)的零极点图

图4 zk·G(z)·P(z)的零极点图

系统的特征方程可以化简为

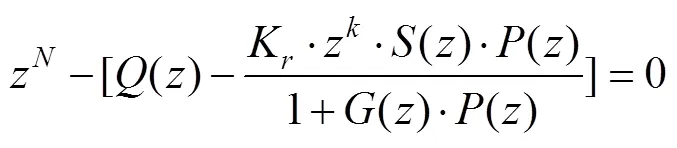
由类似于重复控制中稳定性的判断，根据控制理论中的小增益原理，可以导出复合控制系统稳定的一个充分条件为

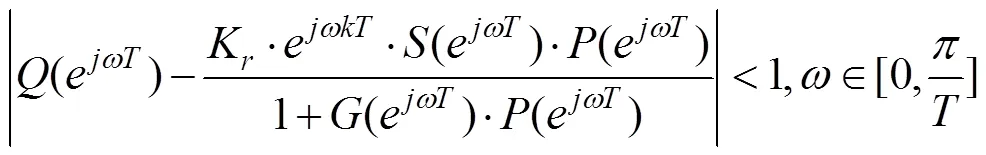
为叙述方便起见，令

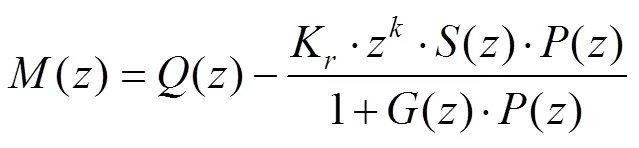
可以通过画出()的幅频响应曲线，来判断系统是否稳定，只要()的幅频响应曲线幅值小于1，系统就是稳定的。

2)准确性

类似重复控制器准确性的推导过程，由前面复合控制方案的基本控制框图可以得出稳态误差在频域中的表达式，为叙述方便起见，令

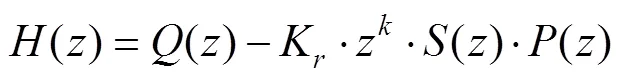
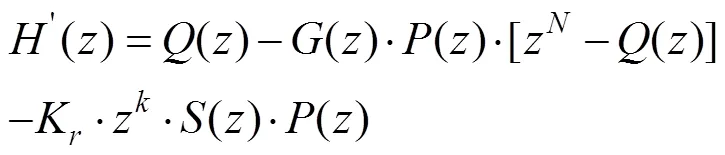
则在频域中的表达式为

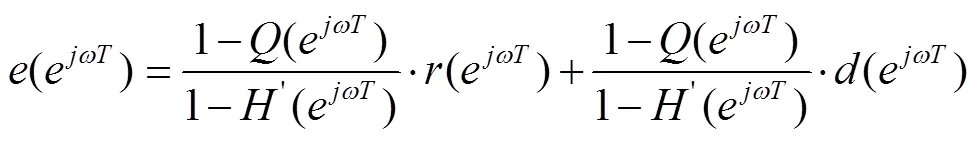
3)快速性

为了便于理论分析，首先做出两个假设：

a)()=1；

b) 指令与扰动是周期重复的，即z·()=()、z·()=()

由误差()的表达式

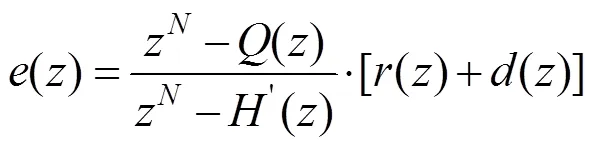
可得

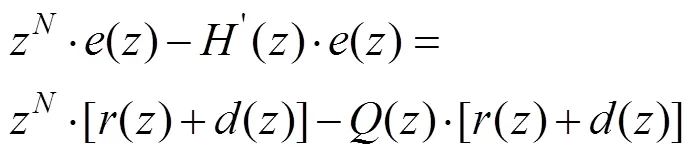
由前面的假设条件可知，上式等式右边为零，所以有下式成立

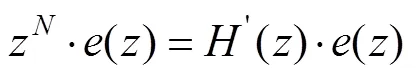
上式表明，每经过一个基波周期的时间，每个采样点上的误差值是上一周期对应采样点上误差值的()倍。显然()幅值越小，误差收敛速度越快。如果针对谐波的误差收敛速度，则可以通过()的幅频响应曲线来观察。虽说这一结论的推导中含有假设成分，但对于研究还是具有指导意义。

现将复合控制方案特性的判定标准总结于表2。

将以上标准作为指导，来进行复合控制方案特性的判定。从以上标准也可以发现，重复控制器与PI控制器并联以后，并不是各自独立的来影响整个控制系统的特性，而是相互关联着同时影响复合控制系统的特性。

3 复合控制方案与重复控制器的特性对比

为了验证复合控制方案的有效性，以一台三相组合式逆变器作为研究对象，逆变器主要参数为：滤波电感1取150 μH，滤波电容取1200 μF，开关频率6 kHz，死区3.5 μs，如下图所示。

重复控制器设计参数如下:

PI控制器设计参数如下:

1)稳定性

我们首先来看，PI控制器和重复控制器并联后的控制系统是否稳定。由前面推导出的复合控制系统稳定的充分条件，()的幅值小于1，画出()的幅频响应曲线，如图7所示。显而易见，复合控制系统满足其稳定的充分条件，所以系统一定稳定。再来与重复控制器稳定的重复条件进行对比，即同时画出()和()的幅频响应曲线，如图8所示。由图8可以观察到到()幅值的最大值为-0.237 dB，()幅值的最大值为-0.358 dB，显然()幅值的最大值更接近于1，复合控制方案的稳定裕度要小于重复控制器的稳定裕度。但考虑到我们所采用的稳定性判据是充分条件，而非充分必要条件，所以判据本身就留有一定裕度，虽然复合控制方案的稳定裕度减小了，但还是可靠稳定的。

2) 准确性

根据前面推导的复合控制方案与重复控制准确性的判定标准，分别画出了(1-())/(1-’())和(1-())/(1-())的幅频响应特性曲线，如图9所示。图9中，低频段(1-())/(1-’())的幅值要远小于(1-())/(1-())的幅值，即低频段复合控制方案的稳态误差小于重复控制器的稳态误差，这是由于复合控制方案中，PI控制器的作用。由于我们的控制是选择在坐标系下，所以指令为直流量，复合控制方案可以对基波做到无静差。而重复控制中由于()的作用，对与直流量的指令也有稳态误差。所以，复合控制方案的准确性要高于重复控制器。在后面的仿真结果中也会验证这一结论。

3) 快速性

根据前面推导的复合控制方案与重复控制快速性的判定标准，分别画出’()和()的幅频响应特性曲线，如图10所示。

可以看到，在中高频段，’()的幅值要小于()的幅值，即复合控制方案的响应速度更快速。这也是由于复合控制方案中，PI控制器的作用。下面通过仿真结果来验证以上结论。利用MATLAB搭建的仿真模型如图11所示。

其中Universal Bridge模块与LC_Filter模块如图12所示。

左侧框图代表的是控制中所要用到的检测反馈给控制器的变量，V_cap框图代表检测到的三相电容电压，Ioabc框图代表检测到的三相变压器副边输出电流（这里没有用到，但后面电流前馈控制会用到）；中间的蓝色框图ctrl就是实现控制算法的s函数；右边的红色框图output是s函数的输出控制量。ctrl框图与output框图之间的框图表示滞后一拍，这是为了与DSP控制中的滞后一拍控制相对应。

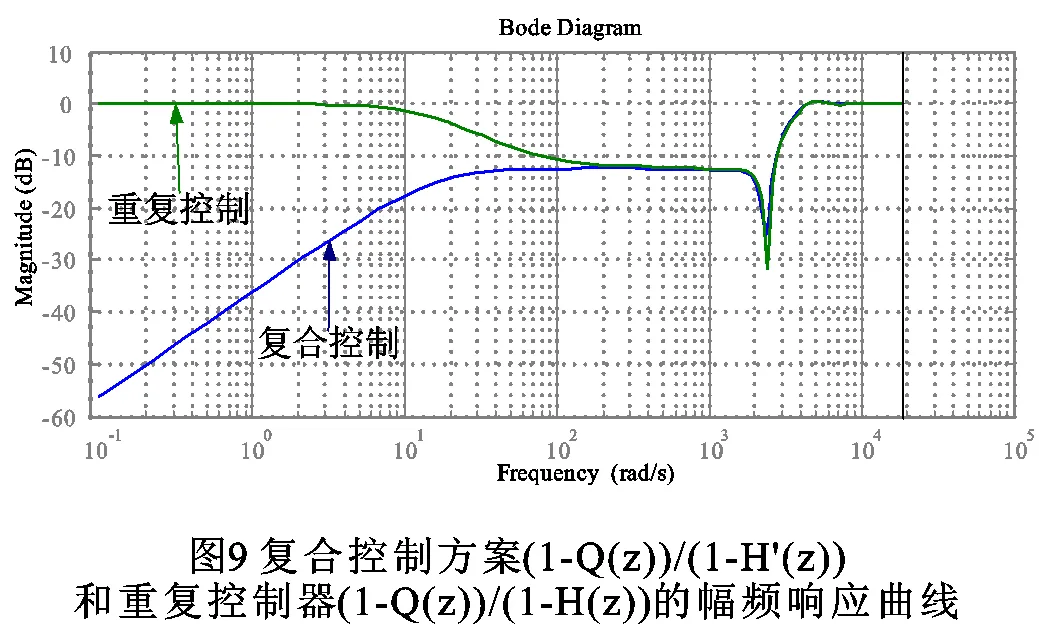
图12 Universal Bridge模块内部电路

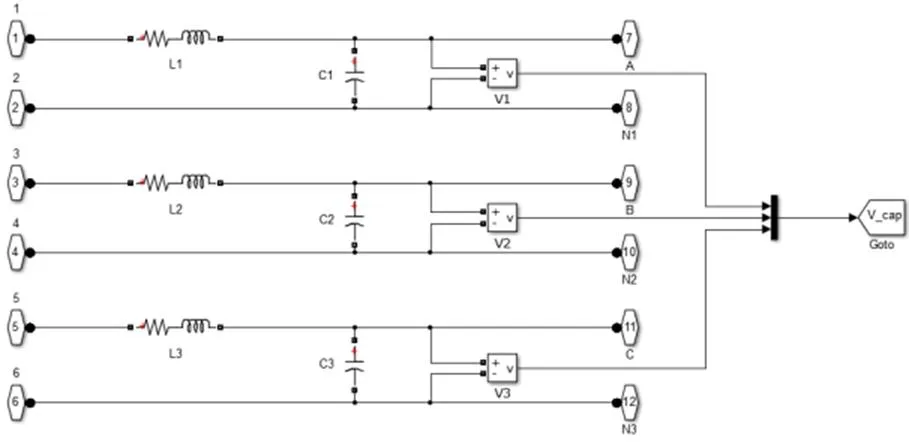
图13 LC_Filter模块内部电路

控制器仿真模型如下

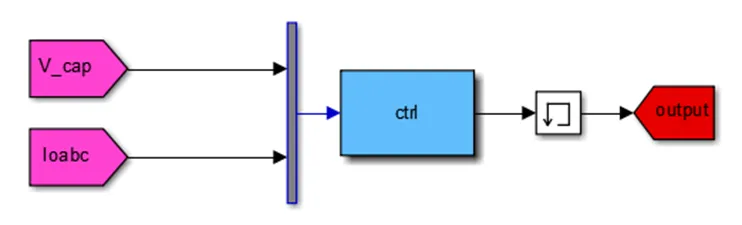
图14 控制器的仿真模型

仿真空载到半载的过程，0.6 s时加载。仿真结果如图15、图16所示。先不看加载过程，从仿真开始，到输出电压稳定，复合控制方案只用了不到0.1 s的时间，而重复控制器用了接近0.6 s；而负载从空载到半载的过程中，复合控制方案只用了不到0.05 s的时间，而重复控制器调节时间至少超过0.4 s。所以重复控制的快速性远不及复合控制方案的快速性。注意，从图15、图16可以发现，两种控制方案输出的电压稳态值不同，重复控制要小于复合控制方案，这也验证了前面进行准确性对比时提出的结论。