大型船舶运动方程辨识方法研究
2017-12-14尚凯林张华军
尚凯林,张华军
大型船舶运动方程辨识方法研究
尚凯林,张华军
(武汉理工大学自动化学院,武汉430070)
针对大型船舶水面二阶运动方程参数辨识问题,提出了一种舵效参数K与时间参数T独立辨识的方法。该方法利用恒舵角机动来辨识舵效参数K,在船舶恒舵角机动完成后,再进一步利用零舵角运动来辨识时间参数T,通过某型船舶的实验测试验证了所提出的辨识算法的有效性。
船舶 运动方程 参数辨识
0 引言
大型船舶由于吨位较大而具有较大的惯性,其操舵响应需要较长时间才能通过航向体现,且船舶运行过程中舵效随着速度而变化,因此大型船舶航向控制系统多 以准确的船舶参数为基础进行控制器设计[1]。为了适应各种海况航行要求,诸如自适应控制[2-4]、滑模控制[5, 6]、反步法[7-9]、神经网络[10-12]、模糊控制[13, 14]等技术分别在船舶航行控制系统中得到应用,通过在线学习的方法直接调整控制器参数而规避了对船舶模型的辨识。虽然上述各种先进控制算法具有较好的控制效果,但是考虑到运行安全和稳定问题,实际应用中多采用变PID控制技术,以不同运行阶段系统参数为基础设计多个PID控制器,根据船舶运行状态动态切换各种控制器以获得最佳的控制效果。鉴于大型船舶实际航行的安全性和稳定性要求,船舶运动方程辨识是系统设计必不可少的环节。

1 船舶运动方程


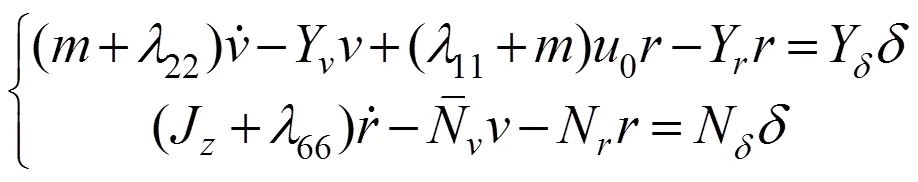
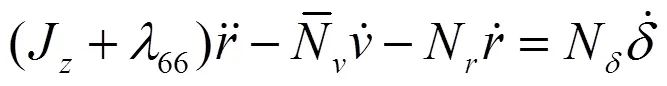

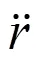
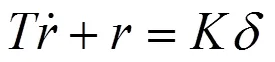
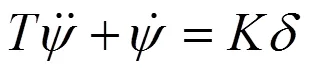
2 模型参数辨识方法


将式(6)按照式(7)形式进行变换,可得其受力分析形式:
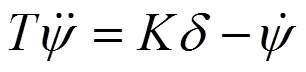
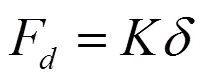
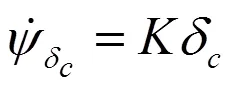
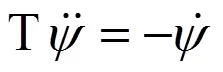

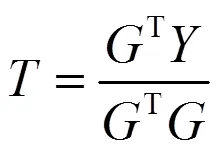
3 实验测试与分析
为了验证本文提出的大型船舶运动方程辨识方法的准确性,本文针对某型船舶在静水域不同航速情况下,利用测量的航向、舵角数据进行了模型参数的辨识,辨识结果如表1所示。
分析辨识结果可以发现,随着航速从6 kn增加到24 kn,系统参数值逐渐增大,而值逐渐减小。参数代表舵效大小,由于低航速时水流对舵叶的作用力较小,所以舵叶产生的转艏推力也较小,从而导致参数较小;而以高航速前进时,由于水流对舵叶的压力增大,相同的舵角能够产生更大的转艏推力,从而导致舵效系数增大。参数代表系统质量(惯性)大小,高航速前进时系统实际质量并没有发生变化,但舵效相对于低航速时增大,此时相同的舵角在高航速时能够产生更大的转艏推力而更快改变航向,于是高航速相对于低航速可等效认为是系统质量减小而易于进行航向机动。
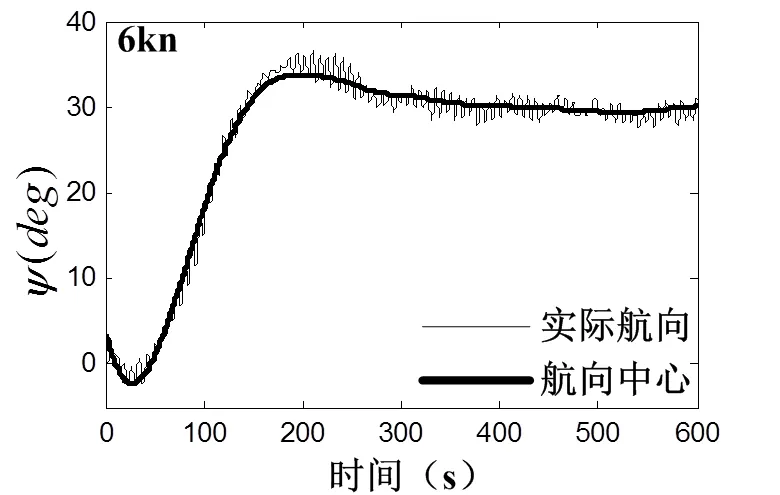
图1 航速6kn时实际航向与预测航向曲线
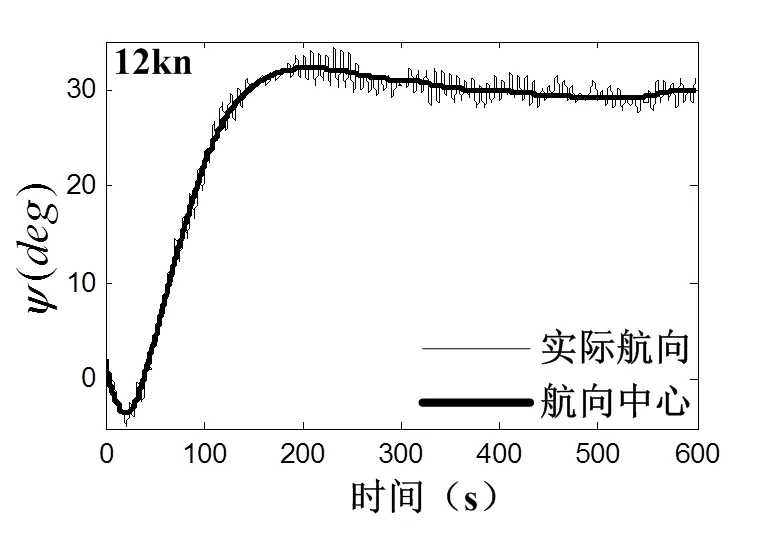
图2 航速12kn时实际航向与预测航向曲线

图3 航速18kn时实际航向与预测航向曲线
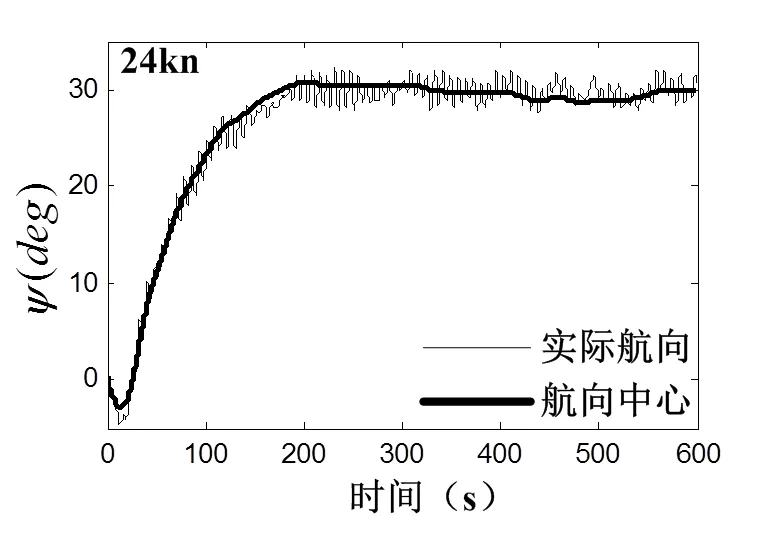
图4 航速24kn时实际航向与预测航向曲线

4 结论
针对大型船舶水面二阶线性K-T运动方程参数辨识问题,本文所提出的分离型辨识方法能够准确获得不同运行状态下的参数值,实船物理实验验证了所提出方法的有效性。
[1] 薛国威,包芸,陈礼建,等. 船舶自动舵控制技术的发展[J]. 中国水运, 2016, 37(7): 47-48.
[2] 林荣智. 利用克隆选择进行船舶航向自适应控制优化[J]. 舰船科学技术, 2017, 39(14): 16-18.
[3] 张洪飞,闫守成. 自适应智能航向控制方法研究[J]. 舰船科学技术, 2016, 38(2): 76-78.
[4] Mitra P, Venayagamoorthy G K. An adaptive control strategy for DSTATCOM applications in an electric ship power system[J]. IEEE Transactions on Power Electronics, 2010, 25(1): 95-104.
[5] 袁雷. 船舶航向非线性系统的多滑模自适应模糊控制[J]. 智能系统学报, 2010, 5(04): 308-312.
[6] Chang W J, Chang K Y. Multivariable performance‐constrained sliding mode control for ship yaw‐motion systems with perturbations [J]. International Journal of Adaptive Control & Signal Processing, 2015, 14(4): 393-409.
[7] 潘永平,黄道平,孙宗海. 欠驱动船舶航迹Backstepping自适应模糊控制[J]. 控制理论与应用, 2011, 28(07): 907-914.
[8] 陈永利,兰洋. Backstepping在船舶航向自适应鲁棒非线性控制器设计中的应用简[J]. 舰船科学技术, 2016, 38(22): 55-57.
[9] 银少海. 滤波反步法在船舶航向自适应控制中的应用[J]. 舰船科学技术, 2017, 39(14): 28-30.
[10] 苏娜,曲美红. RBF神经网络在船舶航向保持非线性控制中的应用[J]. 舰船科学技术, 2017, 39(10): 94-96.
[11] 王欣,刘正江,李铁山,等. 船舶航向离散非线性系统自适应神经网络控制[J]. 哈尔滨工程大学学报, 2016, 37(1): 123-126.
[12] Tang J, Deng C, Huang G B, et al. Compressed-domain ship detection on spaceborne optical image using deep neural network and extreme learning machine[J]. IEEE Transactions on Geoscience & Remote Sensing, 2014, 53(3): 1174-1185.
[13] 甘世红. 基于遗传算法的模糊控制型船舶自动驾驶仪研究[J]. 中国造船, 2011, 52(01): 173-179.
[14] Yuan L, Wu H S. Terminal sliding mode fuzzy control based on multiple sliding surfaces for nonlinear ship autopilot systems[J]. Journal of Marine Science & Application, 2010, 9(4): 425-430.
Research on Parameter Identification of Kinematical Equation for Large Vessel
Shang Kailin, Zhang Huajun
(Wuhan University of Technology, Wuhan 430070, China)
TP 274
A
1003-4862(2017)11-0025-04
2017-10-16
湖北省自然科学基金(2016CFB502,2015CFB586)
尚凯林(1990-),男,硕士研究生。研究方向:运动控制系统设计。
