多颗磨粒微磨削硬脆材料BK7磨削力仿真研究

周 慧，梁志勇

(东华大学，上海 201620)

多颗磨粒微磨削硬脆材料BK7磨削力仿真研究

周 慧，梁志勇

(东华大学，上海 201620)

将金刚石磨粒简化为球形磨粒，从单颗微磨削力模型入手，结合动态磨刃分布模型建立了多颗磨粒微磨削力学模型；结合FME和SPH的方法建立磨粒随机分布的多颗磨粒微磨削力模型；利用所建立的力学预测模型和仿真模型，对不同进给速度和磨削深度时所对应的微磨削力进行研究，并将模拟结果与试验进行对比。结果表明：所建仿真模型可实现多颗磨粒立式微磨削的过程，且结果与试验结果吻合较好，为后续研究多颗磨粒微磨削仿真奠定了基础。

多颗磨粒；微磨削；FME；SPH

随着现代尖端科技朝着微型化、精密化发展，高质量的微零件和微结构元件的制造对我国具有非常重要的战略意义。硬脆材料因其高硬度、高强度、高耐磨性、高热强性以及耐腐蚀性和能承受复杂应力等一系列优良的机械物理性质，广泛应用于航空航天、光学等领域。细微磨削指采用超微颗粒的砂轮在机械表面上进行微纳米机械去除的加工方法，是目前实现微小精密硬脆材料零件的重要方法。因此研究硬脆材料的微磨削力的产生及影响具有深刻的意义。

许多学者从单颗磨粒入手建立了磨削力模型。黄辉和林思煌[1]等对不同形状的金刚石磨粒进行单颗磨粒磨削实验，得到了磨削力的分布曲线：法向力呈驼峰形，切向力有所波动，并且得到最大磨削力的位置；顺磨与逆磨对磨削力的分布曲线没有明显的影响。余剑武和刘智康[2]等建立了单颗CBN磨粒磨削合金钢20CrMo的力学和仿真模型，研究了微观角度的切削成屑机理，并得到磨削速度、前角变化及切削深度对磨削力的影响。

上述研究主要集中在单颗磨粒微磨削力建模研究，针对多颗磨粒微磨削建模研究较少。本文以硬脆材料BK7为研究对象，在考虑到磨削时产生裂纹和切屑的过程是一个大变形过程，存在易产生网格畸变导致计算中止的问题，采用了SPH与FEM结合的算法计算。本文基于立式微磨削进行建模分析。

1 多颗磨粒微磨削力学模型的建立

本文从单颗磨粒微磨削力学的模型入手，结合动态磨刃分布模型来推导出立式微磨削过程中多颗磨粒磨削力力学模型。

1.1 动态磨刃密度模型

切屑形成过程中，磨具的表面形貌参数在磨具与工件表面接触中起到重要作用。在磨削过程中，控制切屑形成的最相关的刀具表面参数是参与磨削的动态磨刃数。在已知单颗磨粒所产生效应的情况下，可以通过磨刃数目估算整体磨具的情况。

磨粒随机分布在磨具表面上。磨粒的密度、尺寸和形状均具有随机性。由于磨具中参与磨削的磨粒数目对磨具所受的整体磨削力产生重要的影响，因此，磨具的表面形貌参数对建立一个可靠的磨削力模型具有重要的意义。参与磨削的磨粒数目不仅由静态磨刃密度所决定，还取决于磨削的运动参数。因此，需要建立磨刃密度模型。

动态磨刃数量是由静态磨刃分布情况和磨削的运动条件及动态磨削效果共同决定的。静态磨刃的数目是由磨粒的尺寸，砂轮的孔隙和修整条件所决定。结合磨轮法向力的作用，引入修正系数δ，可得修正静态磨刃密度公式为：

Cs(z′)=A(Z′)k

(1)

Z′=Z+δ

(2)

其中，Cs(z)表示修正静态磨刃密度(每平方毫米)；A表示与静态磨刃数相关的经验常数；磨轮修正径向距离Z′(μm)[3]。

在微磨削过程中，不是所有的磨粒都参与磨削。因此，Hecker等人认为实际参与磨削过程的磨粒密度公式为[4]：

Cd(z′)Cs(z′)(1-Vsh/Vt)

(3)

其中，Vt表示砂轮与工件接触的总体体积；Vsh表示由实际工作磨粒产生的动态阴影体积。

磨轮工作表面的磨粒是否参与切削主要取决于工件与磨轮表面的接触面粗糙度。工作磨粒数随着接触面积的增加而增加。此外，微磨削因其在磨削过程中单位面积的颗粒密度保持不变，从而达到更均匀去除工件材料的效果，所以磨削效果比常规磨削更好。

假设磨具中每个晶粒都作为一个磨削刃，晶粒上的磨削边缘都可以等同于球形边缘。等效球形磨粒的直径都可由工件和磨具之间的几何关系来确定。磨粒的接触圆直径由下式计算得到[5]：

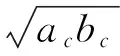
(4)

其中，ac表示切削方向上磨粒的最大接触长度；bc表示磨刃的切削宽度；dc表示磨粒的接触元直径。

当磨粒切削深度t已知，磨粒等效直径dgeq公式为：

(5)

等效磨粒直径的大小取决于磨粒的形状和磨粒切削深度[4]。

切屑生成模型如图1所示。图中弧长l′可由下式计算得到：

(6)

其中t是磨削深度。

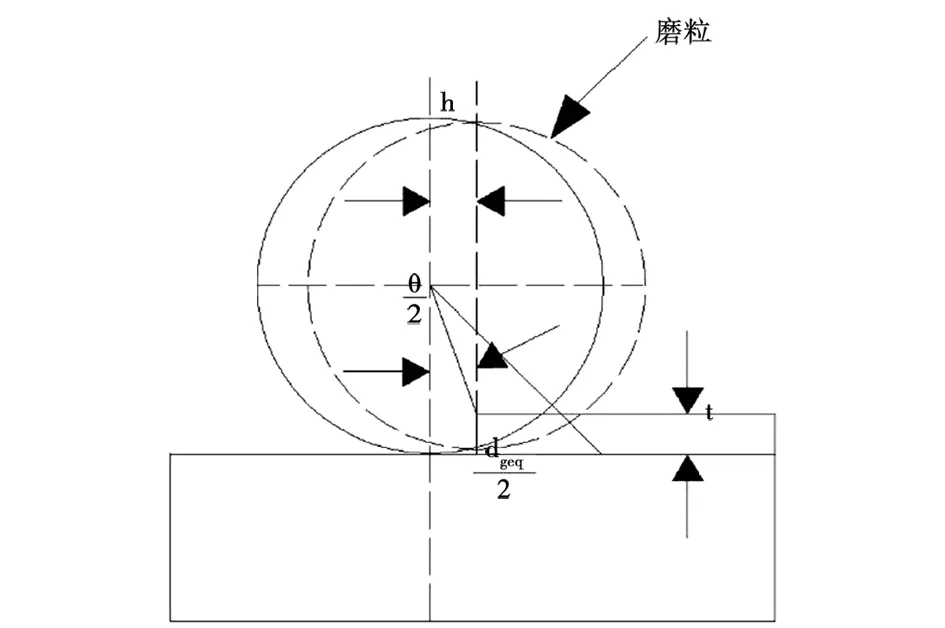
图1 切屑生成模型示意图Fig.1 Chip formation

微磨削过程中，当工件的宽度等于磨具的直径D时，切屑体积可由下式计算：

(7)

其中Am为切屑的横截面积，l为切屑的长度。

因此，在时间t内，切屑的体积Volchip为：

(8)

在同样的磨削时间τ内，工件的材料去除体积Vwp可由下式计算：

Vwp=vtBτ

(9)

由于切削点产生的切屑与整体材料去除率相等，得到未变形切屑厚度[6]：

(10)

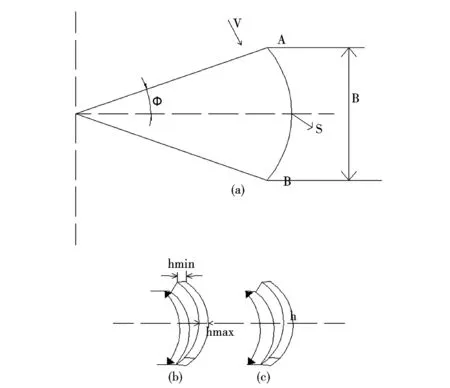
图2 (a)立式微磨削示意图；(b)实际切屑形状；(c)理想切屑形状Fig.2 (a)Schematic diagram of the vertical micro-grinding；(b)Actual chip shape;(c)Idealized chip shape

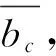
(11)

(12)

线间距L也可由下式计算：

(13)

1.2 单颗磨粒切屑生成力模型

Basuray等提到耕犁力与切屑生成力的转变与临界前角有关。根据几何关系，临界前角可由最小未变形切屑厚度和切削刃半径得到。如下式所示[7]：

(14)

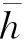
在微磨削中，瞬时前角通过几何关系计算得到。如下式所示：

(15)

当大于最小切削厚度时，微切削机理可以用Merchant模型来描述。本文考虑未变形切削厚度的有限元模型dh。在磨削时，刀具前角位置附近，切屑形成力与摩擦角和刀具前角有关，如图3所示。因此，在二维简化模型中，微切削力增量dfcgx可由下式求得[8，9]：

(16)

其中，dfcgx为材料剪切强度；σs为材料的剪切强度；β为摩擦角；φ为剪切角。

图3 微磨削过程中单颗磨粒作用机理Fig.3 Mechanism of single abrasive particles in micro-grinding process

为了建立单颗磨粒接触模型，将单颗磨粒形状假设为球形。理想的球形磨粒的横截面与切削深度增长率及切削前角的关系如下[10]：

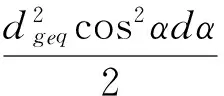
(17)

因此，每单颗磨粒的切屑形成力如下：

(18)

单颗磨粒的切屑形成力法向分力如下：

(19)

1.3 单颗磨粒的耕犁力模型

在微磨削过程中，当切削深度小于产生切屑的最小切削深度时，材料只发生塑性变形而不产生切屑，这个力称为耕犁力。耕犁力在单颗磨粒相互作用的情况下的变化可通过布氏硬度测试。HB定义为负载fbrnl与压痕弯曲面积的比值[11]：

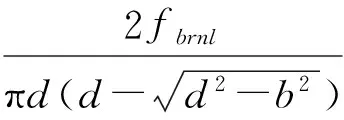
(20)

其中，d为直径；b为压痕直径。

由于耕犁力的影响使得压痕力朝着αcr方向发展。单颗磨粒的总切向力和法向耕犁力结合压痕力和摩擦力的影响来计算。如下式所示：

fpgy=fbml(sinα+μpcosα)

(21)

fpgx=fbml(cosα-μpsinα)

(22)

式中μp为耕犁摩擦系数。

耕犁摩擦系数μp可由Goddard，Wilman和Sin等的预测模型求出。如下式所示[12，13]：

(23)

其中，w为压痕宽度；dgep为球形磨粒半径。

1.4 磨削力理论模型

单颗磨粒的磨削力由切屑生成力和耕犁力组成。计算公式如下：

fn=fcgy+fpgy

ft=fcgx+fpgx

(24)

本模型中，剪切角的大小由Emst和Merchant模型来预测。计算公式如下[14]：

(25)

最终所要求的磨削力Fres可以由三个部分组成：法向力Fn、径向力Fl和切向力Ft，如图4所示。这些力可认为是磨削过程中，单颗磨粒所受的力的合力。计算公式如下：

(26)

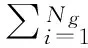
(27)

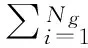
(28)

其中，Ng为动态切削刃数；Fn为单颗磨粒所受法向力；Ft为单颗磨粒所受切向力。

图4 微磨削力示意图Fig.4 Micro-grinding force

2 多颗磨粒的微磨削力仿真模型

2.1 多颗磨粒几何及分布模型的建立

微磨削过程从本质上来说是一种瞬时动态的过程，伴随着大变形、瞬态冲击等，ABAQUS作为一种常用的有限元分析软件，能很好的求解瞬态动力学问题，适用于微磨削。

目前的研究中，主要将磨粒简化为规则的形状，例如：球形、多棱锥形、球形等，本文采用球形模型。

磨粒一般随机分布在磨具表面上，本文在简化磨轮模型时采用随机函数生成随机位置，再将磨粒分布在随机位置上。最终建立立式磨削模型，如图5所示。

图5 立式微磨削建模示意图Fig.5 Finite element modeling for vertical micro- grinding

2.2 多颗磨粒微磨削模型的建立

金刚石磨粒因其较工件材料BK7，具有硬度高、强度大的特点，在磨削过程中不会发生大的形变，遂假设其为刚体。磨粒与工件的材料力学性能如表1所示。

表1 磨粒与工件的力学性能Tab.1 Mechanical properties of abrasive grains and workpieces

考虑到微磨削形成切屑时变形较大，采用有限元法容易产生网格畸变，导致计算终止。SPH采用纯拉格朗日方法，避免了网格畸变问题，适用于求解动态大变形问题，但由于其计算效率较低，且边界处理不如有限元法成熟，所以采用工件材料失效时转化为SPH的方法来建模。划分网格时，将工件与磨具作用区域的网格进行细分，保证仿真精度，远离磨削作用的区域网格进行粗化。在仿真模型中设置相应的参数为：磨具直径为670 μm、进给速度v(1～25 μm/mint)、磨削深度t(0.1～0.5 μm)，对硬脆材料BK7微磨削过程进行仿真。仿真模型如图6所示。

图6 多颗磨粒微磨削的Abaqus仿真模型Fig.6 Abaqus simulation model of multi-abrasive micro-grinding

3 多颗磨粒微磨削的磨削力分析验证

将ABAQUS模型中计算所得的x、y、z三个方向的磨削力输出导出，利用MATLAB进行数据拟合，得到各工艺下的磨削基本稳定的磨削力的大小，与力学模型MATLAB值相对比。并参照文献[15]中实验所得数据，得到图7和图8。

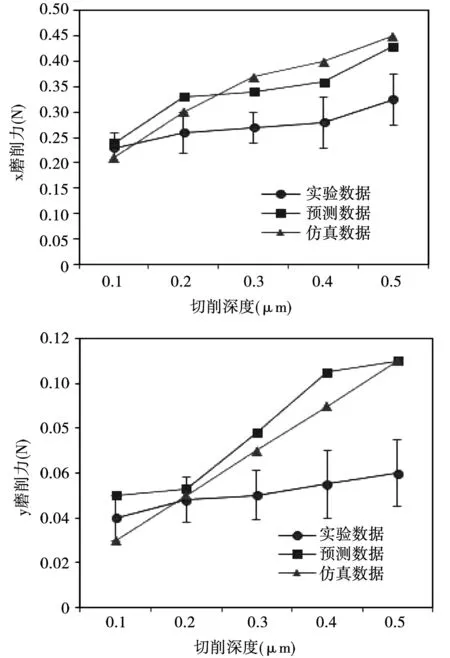
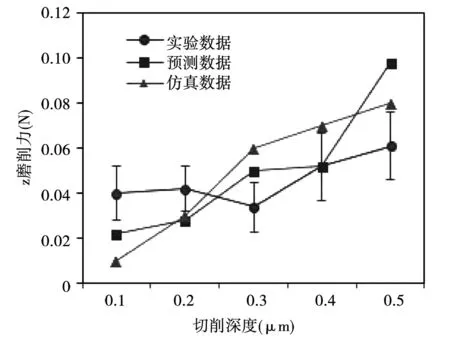
图7 切削深度对微磨削力的影响Fig.7 Effect of depth of cut on the micro-grinding force

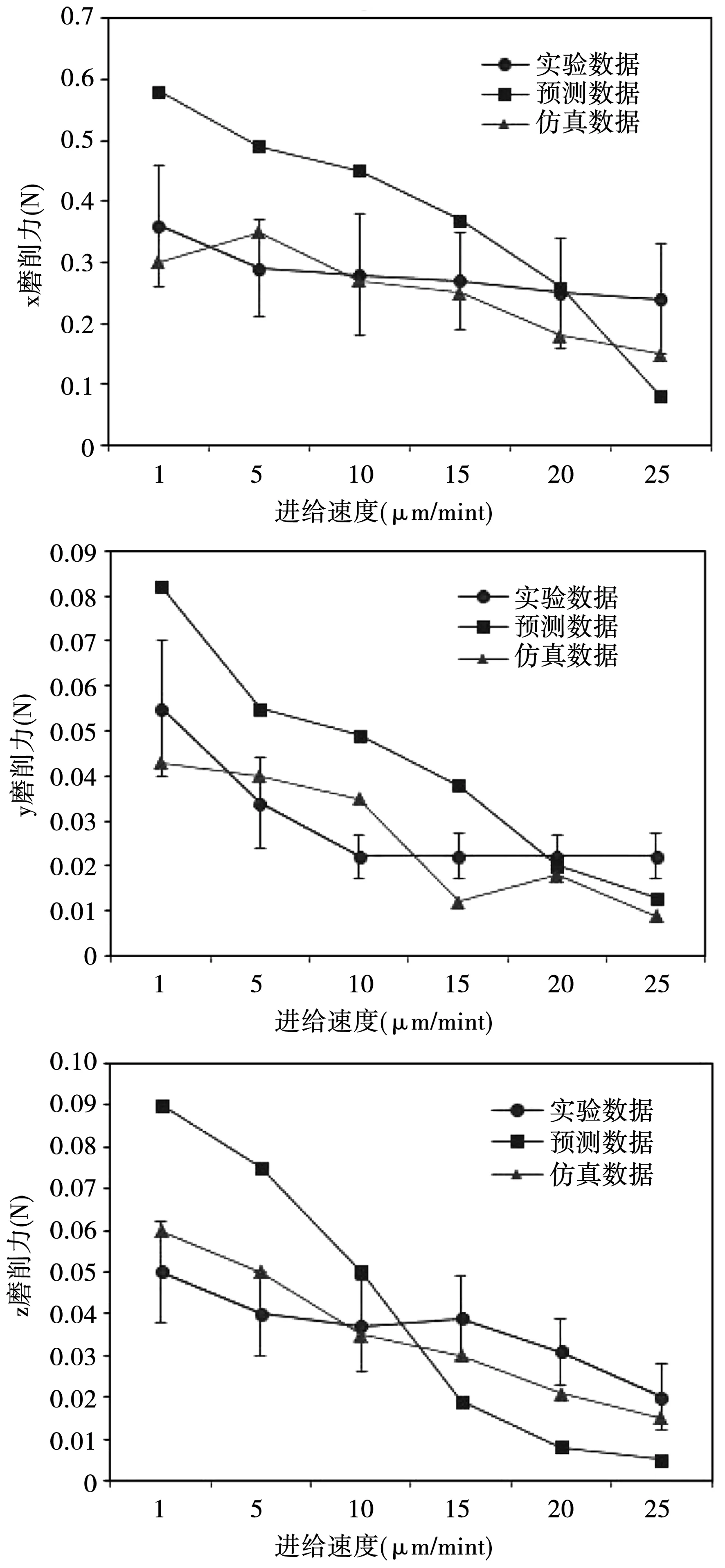
图8 进给速度对微磨削力的影响Fig.8 Effect of feed rate on the micro-grinding force

由图7和图8可看出，力学预测模型和仿真模型在不同切削深度和不同的进给速度下和实验数据具有相同的规律且微磨削力值相仿。可证明仿真模型的正确性。

4 结论

第一，从单颗磨粒微磨削力学的力学模型入手，结合动态磨刃分布模型来推导出立式微磨削过程中多颗磨粒磨削力力学模型。

第二，利用ABAQUS软件，将FME和SPH结合起来建立了磨粒随机分布的多颗磨粒微磨削模型。

第三，力学模型预测结果及ABAQUS仿真模拟结果与实验结果吻合良好，表明提出的建模方法是合理可行的，为研究多颗磨粒微磨削仿真奠定了基础。

[1] 黄辉，林思煌，徐西鹏. 单颗金刚石磨粒磨削玻璃的磨削力研究[J]. 中国机械工程，2010，21(11)：1278-1282.

[2] 余剑武，刘智康，吴耀，等. 合金钢20CrMo的单颗磨粒高速磨削仿真研究[J]. 制造技术与机床，2015，(12)：97-102.

[3] Shaw MC.Principles of abrasive processing[M]. Clarendon, Oxford，1996.

[4] Hecker RL，Ramoneda IM，Liang SY.Analysis of wheel topography and grit force for grinding process modeling[J].J Manuf Proc，2003，(05)：13-23.

[5] Verkerk J, Peters J .Final report concerning CIRP cooperative work on the characterization of grinding wheel topography[J].Ann CIRP，1977，(26)：385-395.

[6] Srihari G，Lal GK.Mechanics of vertical surface grinding[J].J Mat Proces Tech，1994，(44)：14-28.

[7] Basuray PK，Misra BK，Lal GK.Transition from ploughing to cutting during machining with blunt tools[J].Wear，1977，(43)：341-349.

[8] Liu K，Li XP.Modeling of ductile cutting of tungsten carbide[J]. Trans NAMRI/SME，2001，(29)：251-258.

[9] Son SM，LimHS，Ahn JH.Effects of the friction coefficient on the minimum cutting thickness in micro cutting[J]. Int J Mach Tools Manuf，2005， 45(4-5)：529-535.

[10] Park HW, Liang SY.Force modeling of microscale grinding process incorporating thermal effects[J]. Int J Adv Manuf Techn，2009，44(5-6)：476-486.

[11] Shaw, MC. Fundamentals of grinding. In: Proc of the int’1grinding conf. on new developments in grinding[J].Pittsburgh，1972，PA,April,：221-258.

[12] M Goddard J,WilmanH.A theory of friction and wear during theabrasion of metals[J]. Wear，1962，(05)：114-135.

[13] Sin H, Saka N, Suh NP .Abrasive wear mechanisms and the grit size effect[J]. Wear，1979，(55)：163-190.

[14] MerchantME.Mechanics of metal cutting process, and type 2 chip[J]. J Appl Phys，1945，(16)：318-324.

[15] Asma P，M.rahman, Y. S. Wong.Modeling and simulation of cutting forces generated during vertical micro-grinding[J]. Int J Adv Manuf Techn ，2014，(71)：1539-1548.

Simulationresearchonmicro-grindingforceofBK7basedonmultiabrasivegrainscutting

ZHOU Hui, LIANG Zhi-yong

(Donghua University, Shanghai 201620, China)

The typical diamond abrasive grain is simplified into sphere. Micro-grinding force model of multi abrasive grains is set up based on combine the grinding force of single abrasive grain and the model of dynamic cutting edges. A multi abrasive micro grinding force simulation model based on FME and SPH was established. Based on the established mechanical prediction model and simulation model, the micro grinding force corresponding to different feed rate and grinding depth is studied, and the simulation results are compared with the experimental results. The results show that the simulation model by built can realize the vertical micro grinding with multiple abrasive grains process; and the whole process is in good agreement with the experimental results. It can lay the foundation for the simulation of multi abrasive grains micro grinding.

Multi abrasive grains; Micro-grinding; FEM; SPH

TG580.614

A

1674-8646(2017)21-0001-05

2017-10-20

周慧(1993-)，女，研究生。

梁志勇(1966-)，男，工学博士，副教授，e-mail：zhyliang@dhu.edu.cn。