基于数值计算的离心通风机无叶前导器优化研究

陈伟

(山西锦兴能源有限公司肖家洼煤矿，山西 吕梁 033600)

基于数值计算的离心通风机无叶前导器优化研究

陈伟

(山西锦兴能源有限公司肖家洼煤矿，山西 吕梁 033600)

通过Fluent数值模拟软件，寻求能够进一步找到改善离心通风机无叶前导器的方法及最佳工况。对无叶前导器进行建模，变量主要为蜗壳宽度和蜗壳进口张开度，用Gambit进行网格划分，在Fluent设置中改变进口流量的大小。基于一个基础工况，改变相关参数进行研究。之后，通过气动数值模拟及相关公式，得出此次设计的两个重要系数——阻力系数和旋度系数，由这两个系数探究无叶前导器优化的方向。结果表明，流量比、蜗壳宽度和蜗壳出口张开度的增加都有利于阻力系数的减小。

无叶前导器；离心通风机；阻力系数；旋度系数

0 引言

离心风机主要依靠机械能作为其动力源，用于提高气体压力，是一种流体机械，属于从动型设备。无叶前导器离心风机很大程度上弥补了有叶前导器离心风机存在的导叶方面的不足，并且无叶前导器在较小的阻力系数下能产生合适的旋绕，损失小[1-5]。

随着切向进气流量的增加，无叶前导器所产生的阻力系数并未出现太大变化，而旋度系数却增强了许多[6-8]，所以，在单位阻力系数下，无叶前导器阻力系数变得越来越大。在相同的旋度系数下，切向进气流量越大，无叶前导器损失小于有叶前导器的损失；在相同的旋度系数下，无叶前导器比有叶前导器有更小的阻力系数。相比有叶前导器而言，虽然无叶前导器对风机进口阻力也有一定的影响，但可以从很多方面进行优化。

1 建模与数值模拟

1.1 建模及网格划分

建模过程是将2个零件组成1个装配体，即无叶前导器。2个零件分别为蜗壳和带有进气口和出气口的圆柱体。

用Gambit进行网格划分，网格划分基本可以分为面划分和体划分。面划分即Mesh Face，包括三角形网格Tri、四边形网格Element Quad以及混合网格。体划分即Mesh Volume，包括六面体网格Element Hex；以六面体为主，在合适的位置包含一些楔形网格Hex/Wedge；以四面体为主，在适当的位置包含一些楔形、六面体和锥形网格Tet/Hybrid[9-12]。

网格的质量对后面的数值计算具有重要影响，好的网格使最后的计算结果更精确，本文采用的网格如图1所示。

图1 风机结构网格

1.2 Fluent数值模拟

Fluent采用计算流体动力学(CFD)的数值模拟技术，良好的数值模拟与完善的网格使结果具有很高的精度[13]。Fluent采用多重网格加速收敛的技术和多种求解方法，可以达到很高的收敛速度和求解精度，可以用来模拟从不可压缩到高度可压缩范围内的一些复杂流动。基于解的自适应网格技术、储备丰富的物理模型和方便的非结构化网格，Fluent在层流、湍流、多相流、化学反应等方面有广泛应用。将建好的模型在Fluent中进行数值计算[14-15]。

2 控制变量法寻找最佳方案

2.1 阻力系数和旋度系数的计算方法

(1)阻力系数Cf。

表1 10090工况下各数值

式中：p为压力，Pa；v为速度，m/s；ρ为密度，kg/m3；qV为体积流量，m3/s；下标i表示进口；下标o表示出口；下标1,2表示进口1,2端。

(2)旋度系数Cr。

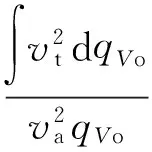
式中：vt，va分别为出口气流的切向速度和轴向速度；qVo为无叶前导器出口总流量。

初始工况：蜗壳进口张开度A=740 mm，蜗壳进口宽度B=520 mm，初始流量qV=7.2 m3/s。

2.2 不同蜗壳宽度和进口张开度下，流量比对旋度系数和阻力系数的影响

2.2.1A为100%原值、B为90%原值(10090工况)流量比与两系数的关系

当流量比为3∶7时，进口2端全压偏大。从极限思想考虑，当进口1的流量无穷小、进口2的流量无穷大时，进口2端总压力趋近于无穷，与实际情况不符且对机器损失较大。流量比为5∶5时是分界点，即流量比小于1时，随着比值的增大，进口1端和进口2端总压减小，出口全压逐渐减少，轴向速度va趋于稳定，切向速度vt逐渐减少，阻力系数和旋绕系数都减少。当流量比大于1时，进口1总压增大，进口2总压减少，出口全压减少，轴向速度稳定，切向速度减少，阻力系数和旋度系数都减少。从极限思想考虑，当比值趋向无穷大时，切向速度为0，没有阻力影响，旋度系数趋向0，这与本次研究相违背，对设备伤害较大，没有实际意义。出口全压在流量比为1.5时有个变化，但其余情况逐渐减少，可能是qVi1较大的原因。

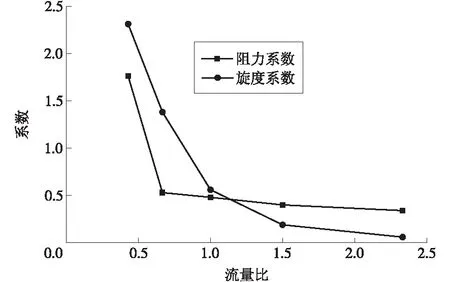
图2 10090工况下阻力系数、旋度系数和流量比的关系

10090工况下各数值见表1，流量比与阻力系数和旋度系数的关系如图2所示。

从图2可以看出，阻力系数和旋度系数都随流量比的增大而减小，且在流量比小于0.67的区间内阻力系数变化较快，之后基本不变。旋度系数在流量比小于1的区间内变化较大，之后也几乎不变。

2.2.2A，B均为100%原值(100100工况)流量比与两系数的关系

两端的极限思想上一个工况已经考虑，其他工况的极限思想完全相同，此处不再阐述。此处各参数值较上面的工况有很大的改变，随着流量比的增大，进口1全压逐渐增大，进口2全压逐渐减少，出口全压在流量比为1.5时有个变化，其余逐渐减少，轴向速度几乎不变，切向速度逐渐减少，阻力系数和旋度系数都减少。

100100工况下各数值见表2，流量比与阻力系数、旋度系数的关系如图3所示。从图3可以看出，阻力系数和旋度系数都随流量比的增大而减小，且在流量比小于0.67区间内阻力系数变化较快，之后基本不变。旋度系数在流量比小于1的区间内变化较大，之后也几乎不变。

2.2.3A为100%原值、B为110%原值(100110工况)流量比与两系数的关系

随着流量比的增加，进口1端总压力逐渐增加，进口2端压力逐渐减少，全压变化同上，轴向速度稳定，切向速度减少，阻力系数和旋度系数均减小。

100110工况下各数值见表3，流量比与阻力系数、旋度系数关系的如图4所示。从图4可以看出，阻力系数和旋度系数都随流量比的增大而减小，且在流量比小于0.67的区间内阻力系数变化较快，之后基本不变。旋度系数在流量比小于1的区间内变化较大，之后也几乎不变。

表2 100100工况下各数值

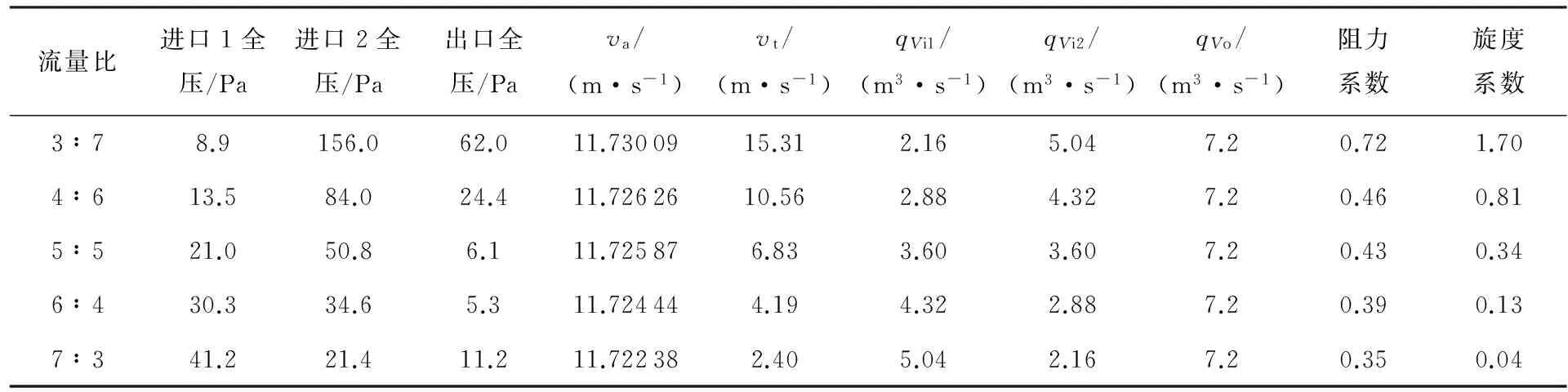
表3 100110工况下各数值

图3 100100工况下阻力系数、旋度系数和流量比的关系

图4 100110工况下阻力系数、旋度系数和流量比的关系

上述3种工况结论几乎一致，无法确定最优工况，在相同的旋度系数下，阻力越小，越有利于风机的节能。在相同的阻力系数下，旋度系数越大，越有利于改善风机的运行特性。为进一步分析最优工况，将阻力系数作横坐标，旋度系数作纵坐标，画出阻旋曲线，如图5所示。

图5 阻旋曲线

由图5可知，在阻力系数小于0.5时3个工况的旋度系数几乎重合，并无优劣区分，即B值变化不影响阻力系数和旋度系数的对应关系。根据3种工况之后的倾斜程度，相同的阻力系数下，选择最佳旋度系数，对风机的运行工况有很大改善，但阻力系数和旋度系数同增，两者不可兼得，追求其中一个最佳工况，另一个值必定不利于风机运行。接着，观察同一旋度系数下阻力系数变化情况，同样的，在旋度系数小于1时，3种工况几乎重合。而对于10090工况而言，在流量比达到0.67时阻力系数增加很小，旋度系数增加了0.40，变化明显，能很好地改善风机的运行特性。鉴于阻力系数0.35到0.50变化不大，而旋度系数0到1.5变化明显，所以在控制流量比为0.67的前提下，选择10090工况能很好地改善风机运行特性。还能得出的结论是：流量比大于1后，B值变化和流量比变化对阻力系数几乎无影响；流量比增大，阻力系数必减小；随着B值的增大，同样的流量比下，阻力系数减小。

3 数值模拟的后处理

基本思想还是控制变量，首先控制蜗壳进口张开度和宽度不变(A为80%原值、B为90%原值)，改变流量比的大小，作出各工况速度矢量图。其中在Fluent里设置一个截面，基于本次模拟z方向总长为0.2 m，z为0.1 m时设置一个面，即为无叶前导器中心部分。

由图6～图9可以看出：随着流量比的增大，蜗壳中心部分周围黑色圆环即圆筒的外边缘密集程度逐渐降低，即旋绕剧烈程度降低；但流量比为7∶3时，却与趋势相反，由上面数据可知，出口压力在该流量比下有上涨的趋势，出口全压损失小，表明失去少的能量同时促进了预旋程度，同时，由于切向进气减少，旋度系数降低。从速度云图可以看出，速度在无叶前导器中的分布无规律，为非对称性流动，圆筒边缘及内部速度较大，即轴向速度和切向速度交汇部分速度较大，并且最大速度部分有明显的位移现象，从而说明了有旋度存在，也减少了有叶前导器由于存在导叶所引起的节流损失，说明研究无叶前导器对风机优化运行有一定的优势。

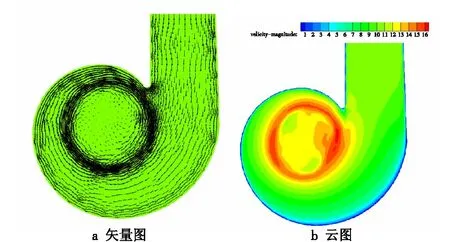
图7 流量比为5∶5时的速度图

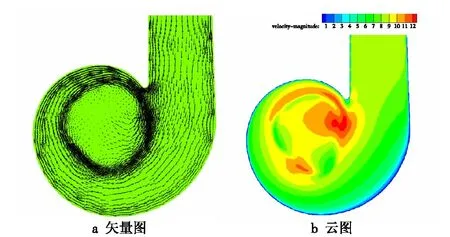
图8 流量比为6∶4时的速度图

图9 流量比为7∶3时的速度图

下面固定流量比(4∶6)和蜗壳出口宽度(B为90%原值)不变，改变出口张开度的大小。

由图10～图12可以看出：随着A值的增大，圆筒周围左半部分明显变得稀疏，即旋度降低；蜗壳中心处深色部分明显减少，即预旋剧烈程度降低，但速度变化并无规律可循，说明了其运动的不规则性。

图10 A为80%原值时的速度图

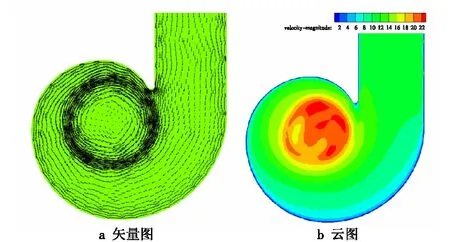
图11 A为90%原值时的速度图

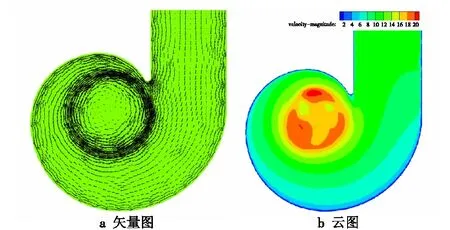
图12 A为100%原值时的速度图

4 结论

速度云图和分布图更加直观地照应了上面的数值计算，但是，B为110%原值工况和流量比为7∶3工况均为转折工况，变化程度与趋势相反，说明A为100%原值、B为110%原值工况与其他工况的曲线不同，B为110%原值可能起到了主导作用。

[1]徐伟,陈更林,赵晋云.基于前导器调节的离心式通风机特性研究[J].矿山机械,2015(5)：28-31.

[2]白硕玮，陈建峰，白念玉.离心式通风机的前导器调风方法分析与研究[J].煤矿机械，2010，31(9)： 177-179.

[3]徐伟，陈更林，赵晋云.离心式风机有叶与无叶前导器特性及机理研究[D].徐州：中国矿业大学，2014.

[4]中国产业调研网.2015—2020年中国离心风机行业现状调研分析及发展趋势研究报告[R].北京：中国产业调研网，2017.

[5]土木工程网.国内发电厂离心通风机的应用现状与经济分析[R].赣州:土水工程网,2011.

[6]中国产业调研网.2015年离心风机现状及发展趋势分析[R].北京：中国产业调研网，2015.

[8]陈更林,杨胜强.通风机调节运行的经济性研究[J].煤矿机电,2007(6)：15-18.

[9]ZHANG M G,LI X G,LIU J C,et al.Flow field simulation and performance analysis of a multi-blade centrifugal fan[J].Chemical engineering,2011,39(11)：51-55.

[10]YU Z，LI S，HE W，et al.Numerical simulation of flow field for a whole centrifugal fan and analysis of the effects of blade inlet angle and impeller gap[J].Hvac amp; R research，2005，11(2)： 263-283.

[11]MAO Q.Layered design of a multi-blade centrifugal fan impeller[J].Mechanical science amp; technology for aerospace,2010,29(10)：1337-1401.

[12]JADHAV N S,PATIL S R.Effects of volute tongue clearance and rotational speed on performance of centrifugal blower[J].International journal of scientific research engineering amp; technology，2016，4(2):261-266.

[13]邓敬亮.离心风机全三维数值模拟及优化设计研究[D].西安：西北工业大学,2015.

[14]王松岭,论力勇.基于FLUENT的离心风机内部流场三维数值模拟及节能改造研究[C]//中国动力工程学会第三届青年学术年会论文集,2007.

[15]汤以兴.通风系统离心风机蜗壳的优化设计[D].沈阳：沈阳工业大学,2014.

(本文责编：刘芳)

陈伟(1990—)，男，陕西镇安人，工程师，从事煤矿机电运输、机电工程及设备运行方面的工作(E-mail:785515585@qq.com)。

TH 432

A

1674-1951(2017)11-0005-05

2017-10-10；

2017-10-22