数学建模中的高维数据挖掘技术优化研究

(晋中职业技术学院，山西 晋中 030600)

数学建模中的高维数据挖掘技术优化研究

闫婷婷

(晋中职业技术学院，山西晋中030600)

高维数据挖掘由于特征空间占用开销较大，挖掘的复杂度较高，挖掘精度不高，为了提高对高维数据挖掘的准确性能，提出一种基于相空间重构和K-L变换特征压缩的高维数据挖掘数学建模方法；采用集成学习技术,对高维数据信息流进行相空间重构处理，考虑类间的数据不平衡性，求得高维数据的关联维特征参量，根据数据的链距离进行稀疏性融合，计算高维数据流模型的最大Lyapunove指数谱，根据谱分析方法实现数据聚类，对聚类后的数据采用K-L特征压缩方法进行降维处理，降低数据挖掘的内存及计算开销；仿真结果表明，采用该方法进行高维数据挖掘，数据挖掘的准确概率较高，占用内存消耗较少，计算开销较小。

数学建模；高维数据；挖掘；特征压缩；数据聚类

0 引言

大数据信息处理是网络技术发展需要面对的关键性问题，数据信息处理包括数据挖掘、数据聚类、数据融合和数据存储，其中，数据挖掘是实现数据库访问和网络信息传输的基础，通过数据挖掘，提取数据信息流的有用特征，满足用户在数据检索中的个性化需求。在网络的云存储空间中，为了降低存储开销，数据多以高维状态形式存储，对高维数据的有效挖掘，为了网络技术发展和信息传输提供高效、个性化、高增值率的应用服务，研究高维数据挖掘方法在计算机信息处理领域具有基础性的应用价值[1]。

数据挖掘在于从海量数据中挖掘出有效的信息特征参量，因此数据挖掘的过程也是对大数据信息流的特征提取过程，传统方法中，对数据挖掘方法的研究主要归为以下几类：基于统计信息处理方法[2]、基于信息融合聚类分析方法、基于信息检索挖掘方法、基于数据集的分布规律差异性分析方法、基于网格分布式计算方法等[3]。上述方法通过提取数据集符合某种统计规律的特征信息，结合相关的数据检索和几何学分析方法，利用数据对特征空间分布维度的敏感性，实现数据挖掘，从而针对性地研究数据的分布规律，提高挖掘的精度和效率，取得了一定的研究成果。其中，文献[4]中提出一种基于Kullback-Leiber距离迁移仿射聚类的云高维数据并行计算方法，对数据信息流进行互信息特征提取，基于数据并行调度的块匹配方法实现数据挖掘，具有较好的挖掘准确度，但是该方法在处理高维数据挖掘时没有进行降维处理，导致计算复杂度较高，实时性不好；文献[5]中提出一种基于聚类划分的高效用模式并行挖掘算法，对高维数据信息流进行互信息特征提取，通过融合异构特征的子空间迁移学习算法进行聚类分析，实现高维数据的并行挖掘，提高了计算速度，该方法存在的问题是抗干扰能力不强，在面对批量数据处理时容易出现测量误差。针对上述问题，本文提出一种基于相空间重构和K-L变换特征压缩的高维数据挖掘数学建模方法。首先采用集成学习技术对高维数据信息流进行相空间重构处理，然后提取高维数据的关联维特征参量，根据数据的链距离进行稀疏性融合，计算高维数据流模型的最大Lyapunove指数谱，对聚类后的数据采用K-L特征压缩方法进行降维处理，最后通过仿真实验进行了性能测试分析，得出有效性结论。

1 高维数据信息流相空间重构及特征提取

1.1 数据信息流的相空间重构

为了实现对高维数据挖掘的数学建模，针对高维数据的特征维度高的特性，需要采用非线性时间序列分析方法进行高维特征空重构，首先采用集成学习技术对高维数据信息流进行相空间重构处理，在高维空间构成系统的相空间，相空间的一个点代表数据分布的一组特征向量，一个子集A称为吸引子，存在A的一个邻域在数据的分布初始条件存在微小差别下，使高维相空间中的数据聚类中心轨道收缩成吸引子，一旦出现数据异常，数据之间的高度随机性将会出现局部收敛，这成为高维数据特征分布的伪随机特性和分形性，高维数据在相空间中具有分形特性，体现在如下几个方面[6]：

1)高维数据的分形结构之间本身具有确定性和独立性，点的分布式零落散乱，数据特征的分形集存在任意小比例的细节，会导致数据的特征分布具有很强的不规则性，出现类间不平衡；

2)数据在最优类分布模式下，以总体分类精度为学习目标进行信息融合和数据聚类，最优类代表样例存在特征差异性，导致在采用传统的线性时间序列分析方法出现额外的学习代价；

3)从算法处理效率和数据处理精度方面考虑，根据数据的分形特性，将高维数据映射到高维相空间中进行非线性处理，能降低计算开销，在高维相空间中，可以通过分形维数去测量数据特征分布的不平滑、不规则性，结合关联维分析和Lyapunove指数谱提取，实现数据挖掘。

由此可见，通过对高维数据信息流相空间重构，构造一个辅助的相空间，从时间序列出发创建一个多维状态空间，结合统计特征分析方法求得数据属性状态及几何不变量，这些几何不变量包括不动点的特征值等，以此为信息素进行数据挖掘和聚类处理，根据上述分析原理，进行高维数据挖掘数学建模的第一步就是进行相空间重构，根据Takens. F和R. Mane的延迟嵌入定理[7-8]，进行高维数据相空间重构建模，首先给出高维数据的信息流模型为：

(1)

式中，wnk是吸引子的分维数，v(t)为加性高斯白噪声，由非线性差分方程描述高维数据挖掘数学模型在时刻n或t的状态向量，数据的几何特征分布表示为相空间S里的一个点。构建多元数量值函数，在时滞约束向量下得到相空间爱特征分布半正定最小特征解满足：

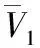
(2)

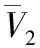
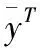
(3)

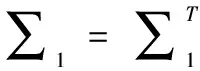
0≤[yT(t)∑TT∑y(t)-fT(y(t))Tf(y(t))]+

[-yT(t)U∑1y(t)+2yT(t)U∑2f(y(t))-fT(y(t))Uf(y(t))]+

[-yT(t-σ)V∑1y(t-σ)+2yT(t-σt)V∑2f(y(t-σ))-

-fT(y(t-σ))Vf(y(t-σ))]

(4)

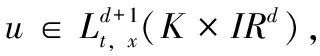
(5)

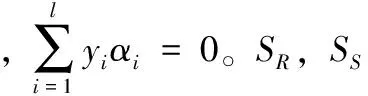
根据上述对高维数据的非线性时间序列分析和相空间重构结果，进行特征提取和数据挖掘数学建模。

1.2 数据属性特征提取

在上述进行了高维数据相空间重构的基础上，考虑类间的数据不平衡性，求得反映高维数据属性类别的关联维特征参量[9]，根据对数据传输可靠性的要求，利用简单的状态空间模型进行数据特征分布的相互关联或相似程度建模，得到数据采样点特征量J1(Wi)可以写为：

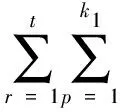
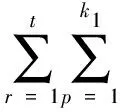
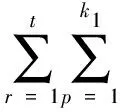
tr(WiTH1Wi)

(6)

式中,

(7)

其中:H1表示高维数据分布随机过程的相互关联，tr(.)表示数据特征分布子带信息分布轨迹，Airp为数据采样的时间跨度。根据连续均匀遍历，考虑类间的数据不平衡性[10]，求得高维数据的关联维特征参量为：

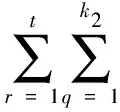
tr(WiTH2Wi)

(8)

式中,

(9)

其中:xir表示主成分特征分量，xirq为模糊核，Birq为稀疏性分布状态值，W为数据的链距离，根据数据的链距离进行稀疏性融合处理，结合特征压缩方法降低数据挖掘的负载。

2 数据挖掘优化数学建模

2.1 最大Lyapunove指数谱计算

在对高维数据信息流相空间重构及特征提取的基础上，进行数据挖掘数学模型优化设计，本文提出一种基于相空间重构和K-L变换特征压缩的高维数据挖掘数学建模方法。根据数据的链距离进行稀疏性融合，考虑数据的离群因子，得到数据的稀疏性表达式为：

(10)

其中，ux和uy为数据对象的二维几何矩，C1表示输出数据序列的不变矩。采用Radon尺度变换在高维相空间中计算最大Lyapunove指数为：

(11)

式中，r1表示数据序列尺度信息分解维数，r2表示先验点簇，σ1表示边缘相关性约束向量，N1为仿射不变矩。

利用数据集的相似k距离邻居序列的尺度不变性，根据谱分析方法实现数据聚类，得到聚类目标函数为：

(12)

其中:J(w,e)为数据对象的分块约束向量，ai为相空间所有对象的一个排列，φ(xi)为噪声敏感系数。

2.2 数据挖掘的K-L特征压缩

采用最大Lyapunove指数谱特征矩阵的奇异值分解方法，设A∈Rn×m，得到挖掘的数据信息特征的K-L变换式为：

(13)

其中:误差项e满足相似k距离邻居分布，对高维数据的最大Lyapunove指数平进行奇异值分解[11]，通过特征压缩，将K-L变换式改写矩阵形式为：

Y=Xβ+e

(14)

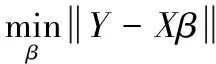
(15)

最后采用自适应学习方法进行误差修正，实现数据优化挖掘的并行处理[12-13]，进行高维数据挖掘的并行计算。

2.3 数据挖掘实现步骤

综上分析，得到高维数据挖掘的优化实现步骤描述为：

1)设置挖掘的初始迭代次数为I=0，参数初始化；

2)对全部物理机路径上的数据点进行初始化，进行相空间重构；

3)分配虚拟机，利用集成学习方法进行测试样本训练；

4)完成所有虚拟机的分配后，遍历每个数据点，利用公式(13)计算数据点的链距离，执行局部信息更新；

5)利用公式(15)进行K-L特征压缩和数据降维处理，在最优分配方案下进行数据聚类，执行全局信息素的更新。

6)假设当前挖掘次数Ilt;Imax，则I=I+1，并跳转到过程(2)，反之跳转到步骤(7)；

7)结束挖掘，输出最优分配方案，得到最优挖掘结果。

3 仿真实验分析

为了测试本文方法在实现高维数据挖掘中的表现性能，进行仿真实验和性能分析，实验硬件配置环境为：操作系统Windows7，Intel(R) Core(TM)2 Duo CPU E7400 2.80 GHz，4 GB RAM，硬盘：500 G，软件为Matlab 7。实验所用的高维数据样本为两个大数据集，其中，CSLOGS数据集表示测试数据集，数据规模为2 000 GB, TEST set 数据集为训练数据集，数据规模为1 000 Mbit，子块分区大小为5.24 Mbit，相空间重构的嵌入维数m=4,时间延迟τ=11，数据采样的频率为12 KHz，采样间隔为1.25 s，数据的干扰信噪比-10～0 dB,根据上述仿真环境和参量设定，进行数据挖掘仿真分析，首先进行原始数据采样，得到采样结果如图1所示。

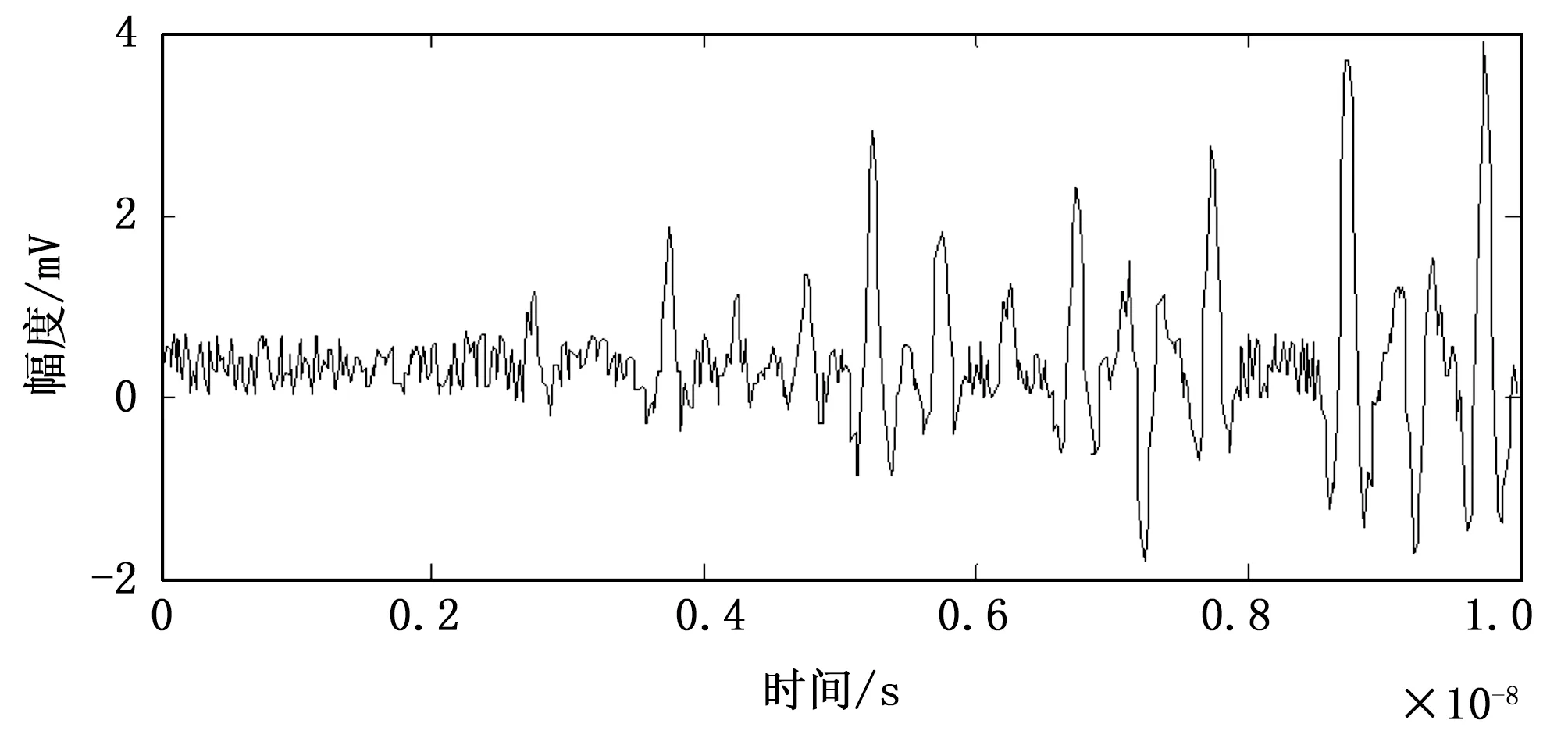
图1 高维数据信息流时域波形

以图1所给出的高维数据采样样本为测试对象，提取最大Lyapunove指数谱，进行数据聚类和特征压缩处理，得到谱特征提取结果如图2所示。

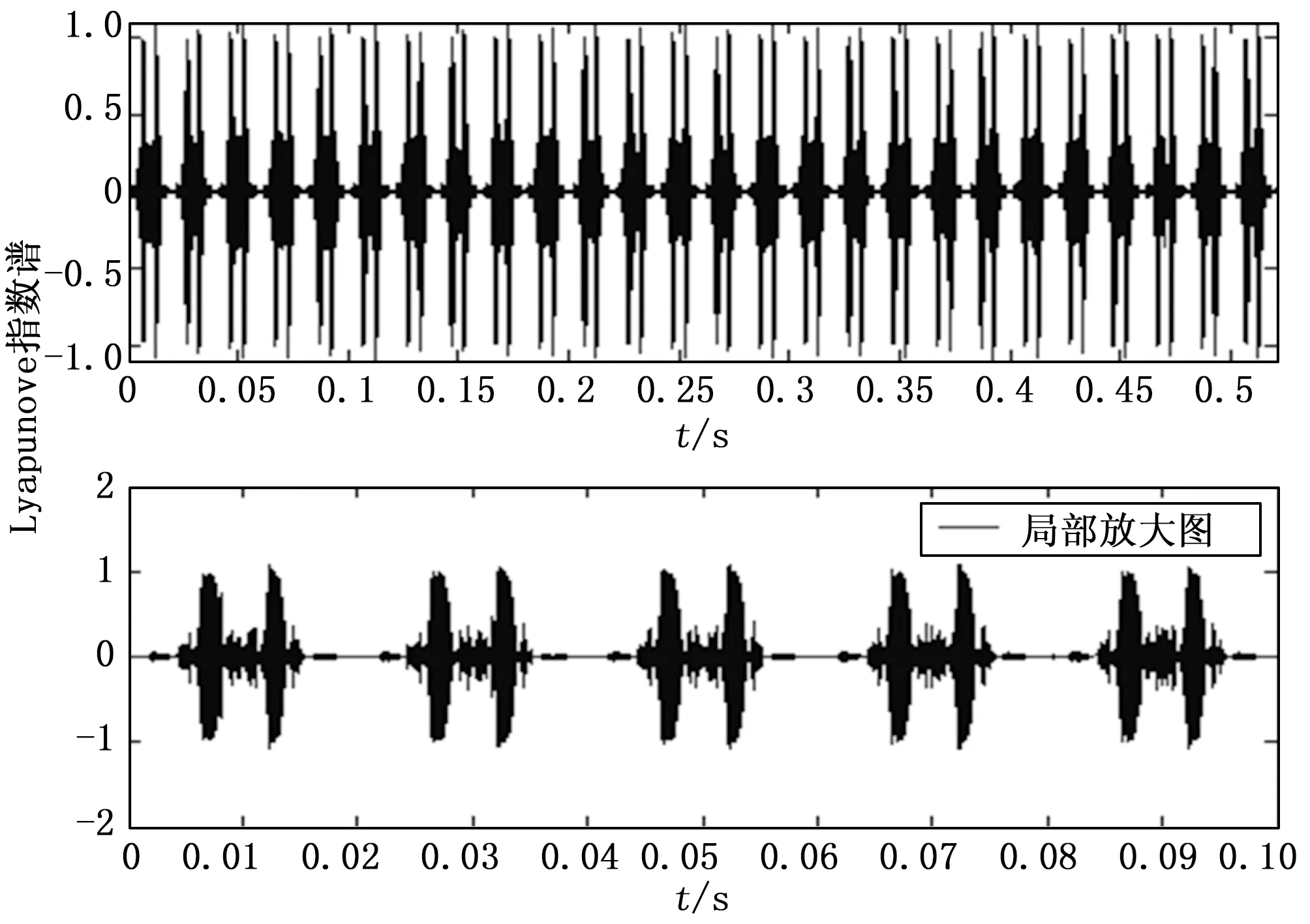
图2 最大Lyapunove指数谱特征提取结果

分析图2结果得知，采用本文方法进行高维数据挖掘，能从受到较大污染的数据序列样本中挖掘到有用的信息特征，挖掘的抗干扰能力较强。图3和图4给出了采用本文方法和传统方法进行数据挖掘的准确性和运行开销对比结果，分析得知，采用本文方法进行高维数据挖掘的准确度较高，因为进行了特征压缩，所以运行开销较小，综合表现性能较优。

4 结束语

本文研究的高维数据的优化挖掘问题，提出一种基于相空

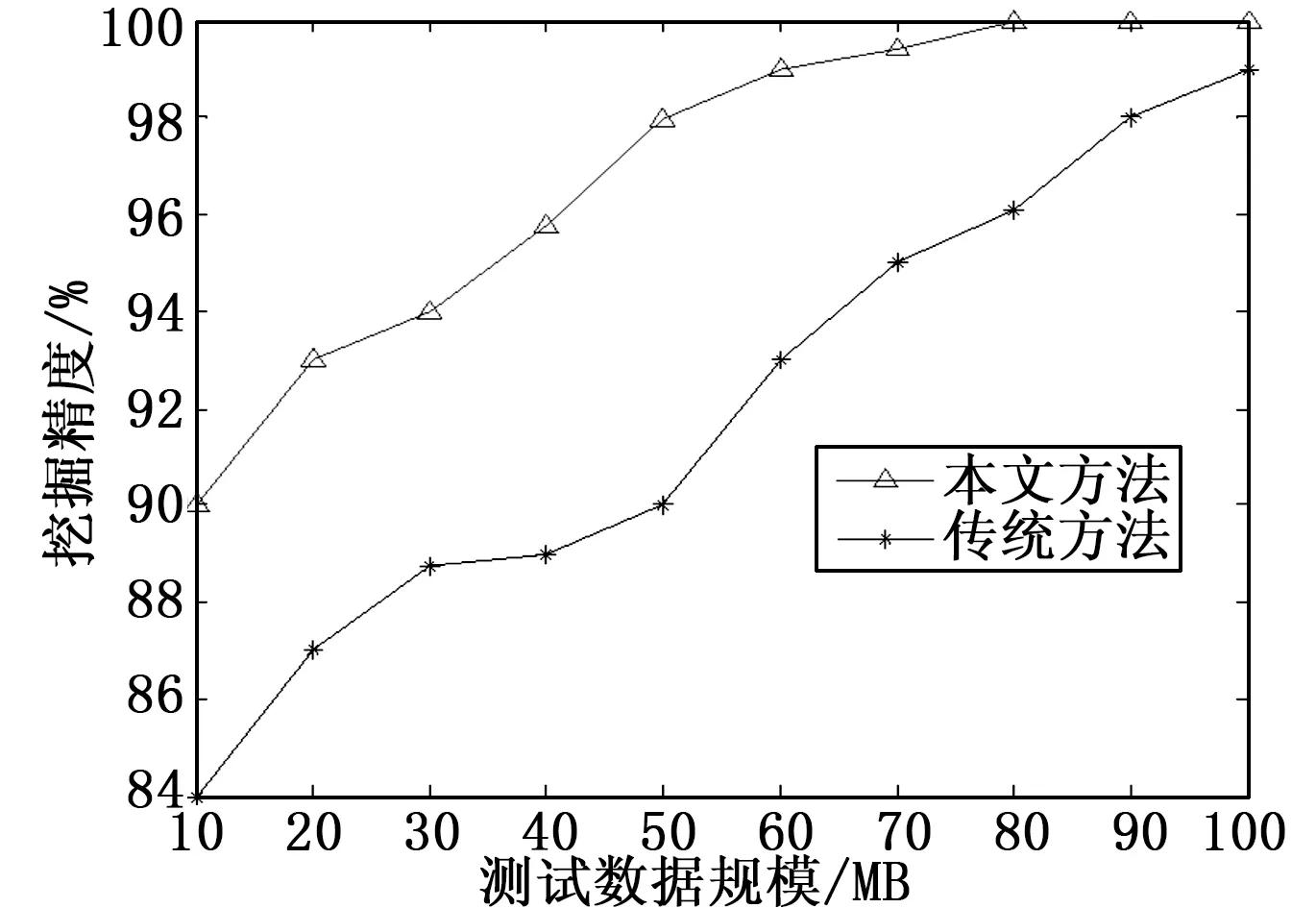
图3 挖掘准确性对比

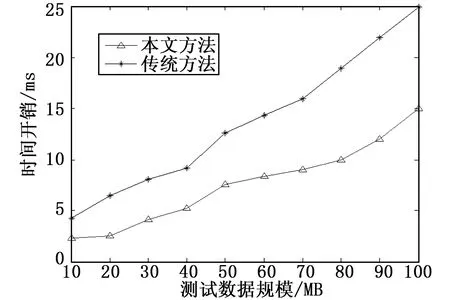
图4 运行时间对比

间重构和K-L变换特征压缩的高维数据挖掘数学建模方法，首先采用非线性时间序列分析方法进行高维特征空重构，求得反映高维数据属性类别的关联维特征参量，然后利用简单的状态空间模型进行数据特征分布的相互关联或相似程度建模，求得最大Lyapunove指数谱特征，通过K-L特征压缩器进行高维数据压缩，采用自适应学习方法进行误差修正，实现数据优化挖掘的并行处理。研究得知，本文方法进行数据挖掘的精度较高，抗干扰性较强，运行时间较短，总体性能占优。

[1] Mernik M, Liu S H, Karaboga M D, et al. On clarifying misconceptions when comparing variants of the Artificial Bee Colony Algorithm by offering a new implementation[J]. Information Sciences, 2015, 29 (10): 115-127.

[2] Hsieh T J. A bacterial gene recombination algorithm for solving constrained optimization problems[J]. Applied Mathematics and Computation, 2014, 23 (15): 187-204.

[3] Long M, Wang J, Ding G, et al. Adaptation regularization: A general framework for transfer learning[J]. IEEE Transactions on Knowledge and Data Engineering, 2014, 26(5): 1076-1089.

[4] 毕安琪,王士同. 基于Kullback-Leiber距离的迁移仿射聚类算法[J]. 电子与信息学报, 2016, 38(8): 2076-2084.

[5] 邢淑凝, 刘方爱, 赵晓晖. 基于聚类划分的高效用模式并行挖掘算法[J]. 计算机应用, 2016, 36(8): 2202-2206.

[6] 邓志刚, 曾国荪, 谭云兰, 等. 云存储内容分发网络中的能耗优化方法[J]. 计算机应用, 2016, 36(6): 1515-1519.

[7] 陆兴华,李国恒,余文权. 基于模糊C均值聚类的科研管理数据库调度算法[J]. 计算机与数字工程, 2016,44(6): 1011-1015.

[8] 毕安琪, 董爱美, 王士同. 基于概率和代表点的数据流动态聚类算法[J]. 计算机研究与发展, 2016, 13(5): 1029-1042.

[9] 赵国荣,韩 旭,杜闻捷，等. 具有传感器增益退化的不确定系统融合估计器[J]. 控制与决策, 2016, 31(8): 1413-1418.

[10] 张 涛,唐振民,吕建勇. 一种基于低秩表示的子空间聚类改进算法[J]. 电子与信息学报, 2016, 38(11): 2811-2818.

[11] Patel V M, Nguyen H V, Vidal R. Latent space sparse and low-rank subspace clustering[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(4): 691-701.

[12] 唐 杰,徐 波,宫中樑,等.一种基于CUDA的三维点云快速光顺算法[J].系统仿真学报,2012,24(8):1633-1638.

[13] 周 煜,张万冰,杜发荣,等.散乱点云数据的曲率精简算法[J].北京理工大学学报,2010,30(7):785-790.

ResearchonOptimizationofHighDimensionalDataMininginMathematicalModeling

Yan Tingting

(Jinzhong Vocationalamp;Technical College,Jinzhong 030600,China)

High dimensional data mining due to the characteristics of the space occupied large overhead mining, high complexity, mining precision is not good, in order to improve the accuracy of performance on high dimensional data mining, this paper brings forward a mining method of mathematical modeling of phase space reconstruction and K-L transform features of high dimensional data based on compression. The ensemble learning technique to reconstruct the phase space of high dimensional data flow, considering the inter class data imbalance, the correlation dimension of the characteristic parameters of high dimensional data, according to the chain distance data sparsity fusion, maximum Lyapunove computation of high dimensional data stream model refers to the number of spectra, the spectral analysis method of data after clustering, clustering of data using K-L feature dimension compression method, reduce the memory and computation overhead of data mining. The simulation results show that the method has high accuracy, less memory consumption and less computation cost.

mathematical modeling; high dimensional data; mining; feature compression; data clustering

2017-03-06；

2017-03-24。

闫婷婷(1983-)，女，山西晋中人，研究生，讲师，主要从事数学与应用数学方向的研究。

1671-4598(2017)09-0158-03

10.16526/j.cnki.11-4762/tp.2017.09.041

TP391

A