多轴疲劳寿命预测方法

赵丙峰，谢里阳，徐国梁，李海洋，张诗健，王博文

(1.东北大学 航空动力装备振动及控制教育部重点实验室，沈阳 110819；2.中国航天科技集团第702研究所，北京 100076)

多轴疲劳寿命预测方法

赵丙峰1，谢里阳1，徐国梁2，李海洋1，张诗健1，王博文1

(1.东北大学 航空动力装备振动及控制教育部重点实验室，沈阳 110819；2.中国航天科技集团第702研究所，北京 100076)

在工程实际中，大多数工程结构和机械零件都承受着各种形式的循环载荷，载荷分布大多呈现多轴应力状态。在循环荷载作用下，对多轴疲劳寿命的研究比单轴的更加接近工程实际，有更广泛的应用背景。针对这一现状，本文详述了近年来国内外关于多轴疲劳寿命预测方法的研究现状，分别介绍了等效应变法、能量法、临界面法三种主流方法的基本原理及优缺点，并将这三种方法做了简单对比。另外，针对现阶段各类多轴疲劳寿命预测方法的不足，提出了今后在多轴疲劳领域研究工作的设想。

多轴疲劳；寿命预测；等效应变法；能量法；临界面法

0 引言

在工程实际中，大多数工程结构和机械零件都承受着各种形式的循环载荷，载荷分布大多呈现多轴应力状态。即使处于单轴外载荷环境中，鉴于构件几何形状的复杂性，其危险部位实际承受的载荷仍呈多轴分布，失效模式同样属于多轴疲劳失效[1]。因此，在循环荷载作用下，对多轴疲劳的研究比单轴疲劳更加接近工程实际，有更广泛的应用背景。

所谓多轴疲劳，是指构件在承受多向应力或应变作用下的疲劳，也称复合疲劳。多轴加载过程中通常有多个应力/应变分量独立地随时间变化，这些应力/应变分量的变化可以是同频率、同相位的，但多数情况下是非同相、非同频的。随着不同应力/应变相对比值及几者间相位差的改变，疲劳裂纹可能在不同的方向、不同的平面内形成[2]。因此，相比于单轴应力状态，多轴应力状态下的材料循环应力/应变特性及裂纹取向、形状、扩展方向、速率等参数均将受到更多因素的影响。

长期以来，工程结构和机械零件的疲劳寿命研究主要集中在单轴加载方面，在单轴疲劳研究领域已形成较为成熟的疲劳寿命评估方法，但是对多轴加载条件下的疲劳问题，尤其是多轴非比例疲劳问题的研究相对还不成熟[3-4]。单轴疲劳和多轴疲劳之间的差别主要体现在循环附加强化的差异上，在等效应变幅相同的情况下，多轴载荷状态下材料的循环附加强化程度明显高于单轴载荷状态，这在宏观的应力-应变响应上表现为等效应变幅下多轴载荷状态下的等效应力幅值更高。而循环应力值的增大可加快疲劳微裂纹的扩展速率，因此多轴载荷加载下较高的等效应力幅值可以大大加快疲劳微裂纹的扩展，从而造成了多轴加载疲劳寿命较单轴加载大大降低。同时，多轴载荷循环加载过程中，材料的附加强化程度还与其层错能有关，另外，对于层错能不高的金属材料，其附加强化效应强烈依赖于非比例加载路径[5]。但是，就工程构件而言，多轴加载有无穷多种组合，即有无穷多种加载路径，如何用有限的参数去描述这无穷多种情况是多轴疲劳问题研究的关键之一。综上所述，工程结构和机械零件的多轴疲劳寿命不仅取决于所施加的应力或应变值的大小，而且还强烈地依赖于加载路径和材料的瞬态行为，因此要给出一个合理的多轴疲劳寿命预测模型十分困难。最早的多轴疲劳估算方法通常是将多轴疲劳损伤等效为单轴情况，然后基于单轴疲劳理论研究多轴加载条件下的疲劳寿命预测方法，主要基于3个准则：最大主应力/主应变准则、Mises等效应力/应变准则、Tresca最大切应力/切应变准则。大量研究发现，对于多轴比例加载，这些准则是有效的，且简单实用，但在非比例加载情况下，上述准则都不能给出理想的预测结果。在之后几十年中，通过众多学者的努力探索[6]，主要建立了三大类多轴疲劳寿命预测模型：等效应变法、能量法、临界面法。但是，对于多轴疲劳寿命预测，迄今为止还没有找到一种能够被广泛接受的方法，大量的试验研究还有待开展下去，本文试图将近几年的研究成果作一个总结，希望能对今后的研究工作有所帮助。

1 多轴疲劳寿命估算方法概述

1.1 等效应变法

在多轴低周疲劳研究的初期，由于客观条件的限制，人们对多轴疲劳的损伤机理并不十分了解。在损伤参数的选择上，延续了单轴低周疲劳寿命预测的思路，选用等效应变作为多轴低周疲劳寿命预测参数，希望借助于该参数将多轴应变的加载状态转化为等效的单轴应变状态，进而估算出构件的疲劳寿命[7]。等效应变法最初是用于单轴低周疲劳的著名Manson-Coffin公式，Manson和Coffin对许多类型的金属材料进行等塑性应变幅下的低周疲劳试验，发现在双对数坐标系下，塑性应变幅和疲劳寿命之间呈线性关系并给出了相应公式，即Manson-Coffin公式。后来，Kanazawa[8]、Socie等[9]学者将其发展用于多轴低周疲劳寿命估算中，并经过Zamrik[10]、Bonacuse等[11]的发展与修正，对于多轴拉压低周疲劳，其公式可表示为如下形式：

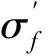
但是在复杂应力状态下，特别是非比例加载时，Coffin-Manson准则不能给出满意的估算结果。对此，在单轴应变等效理论的基础上，Itoh等[12]考虑了多轴加载过程中，不同应变路径下材料附加强化对疲劳寿命的影响，将等效应变幅定义为

式中：Δε1为最大主应变幅；α为与附加强化有关的材料常数；fn为应变路径非比例因子。Itoh模型只是在材料性能上考虑了附加强化的影响，但对于同种材料并未提出明确的参数定义材料附加强化程度的强弱。Borodii[13]在此基础上考虑了循环路径相对于主轴方向的变化，得到如下表达式

式中：Δε为最应变幅；α为与附加强化有关 的材料常数；fn为材料常数；Φ为非比例参数；ψ为加载路径方向与主轴之间的夹角。以上两个模型都是以模糊参数的形式考虑加载路径的影响，Skibicki[14]详尽分析了多轴加载过程中的加载路径形式，用单轴和纯扭疲劳参数作为权，直接从路径中提取数据来求取多轴疲劳寿命

式中：εeq,a为从加载路径中提取到的等效应变，提取过程见图1；εx,a、γx,a分别为加载正应变、剪应变范围；NfA、NfS分别为单独施加εx,a、γx,a时的疲劳寿命。

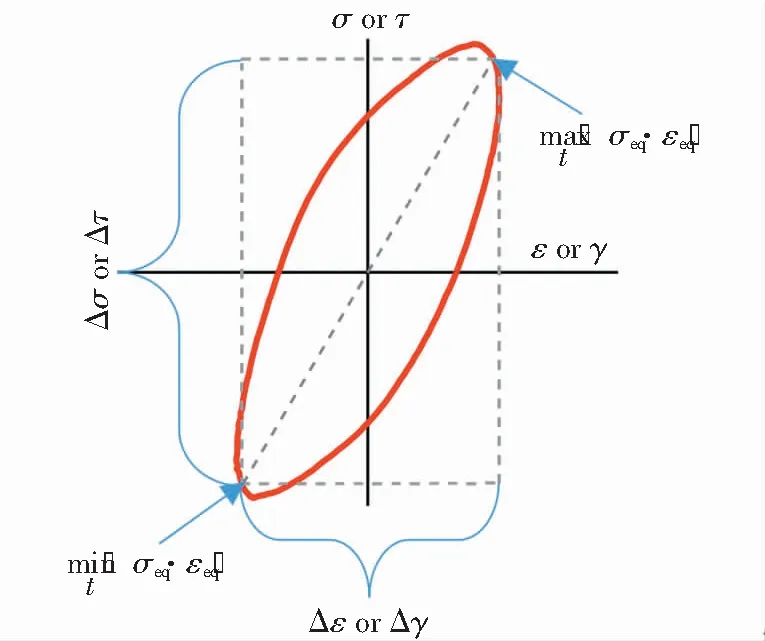
图1 多轴加载路径示意图[14]Fig.1 Schematic diagram of multiaxial loading paths

以上几个模型都是针对多轴低周疲劳提出的，针对多轴高周疲劳，应力往往是表征寿命的理想参数。对此Lee[15]借鉴等效应变法的思路，以应力代替等效应变法中的应变，并对Cough的椭圆方程进行了修改，提出了以应力为参量的寿命预测模型

式中：f0为材料的弯曲疲劳极限；t0为材料的扭转疲劳极限；σb,ben为材料的弯曲疲劳强度；β是材料常数；ψ是弯曲和扭转间的相位差。但Wang[16]认为材料常数β需要通过大量试验数据得出，这在一定程度上限制了Lee准则的应用。

借鉴以上两种思路，为融合应力和应变两者对多轴疲劳寿命的影响，Glinka[17]和Sun[18]都同时考虑了应力和应变对疲劳寿命的影响，并得出了相似的等效应变形式，也有很多学者将这一部分工作归纳到了能量法中。

1.2 能量法

能量法由Morrow提出，其认为塑性功的累积是材料产生不可逆转损伤进而导致疲劳破坏的主要原因。这种方法的核心思想是：在每一次循环中零件或构件由于吸收了外界所施加的能量，从而在其内部产生了不可逆转的损伤，损伤的程度与所吸收的能量多少成正比。损伤逐步累积，一旦达到临界值，零件便由于疲劳而发生失效。能量准则根据每一循环应变能密度类型，可以分为三类[21]：适合于高周疲劳的弹性应变能准则；适合于低周疲劳的塑性应变能准则；适合于低周和高周疲劳的弹性应变能和塑性应变能综合准则。

Ellyin[22]最早应用总应变能密度来拟合多轴疲劳寿命，其模型基于每次循环的总应变能密度，以总应变能密度ΔW作为损伤参量

式中：ΔWe、ΔWp分别为弹性应变、塑性应变能；A、d为材料参数。通过试验证明发现，Ellyin模型对单轴和比例加载下的多轴低、高周疲劳寿命都有较好的拟合性，但并不适用于非比例加载的情况。另外，Ellyin模型没有考虑应变能密度在试样截面上的波动，并且不能应用于缺口试件。之后，Garud[23]进一步发展了塑性功理论并将其推广到多轴疲劳中，推导出如下塑性功与裂纹萌生寿命间的关系

式中：F(Wp)是Wp的单调递减函数，其具体形式可通过试验获得。

随着临界面准则在估算多轴疲劳寿命方面的广泛应用，一些学者开始将临界面法和能量法结合，进而得到一种新的预测多轴疲劳寿命的方法。其中，以Glinka[24]，Pan[25]，Walat[26]，Berto[27]，Branco[28]等的工作较具代表性，其模型的大致形式都可写为

式中：a、b分别为不同模型所采用的不同参数。因这一部分模型结合了临界面法，所以在有些地方这被称为临界面应变能密度法。

1.3 临界面法

1973年Brown和Miller在研究了大量多轴疲劳数据后得出结论：用一个参数描述多轴疲劳已不再有效，在描述疲劳过程时应需要两个应变参数，即一个特殊平面上的循环剪应变和法向正应变，这就是所谓的临界平面法。临界面的概念是建立在疲劳裂纹萌生和扩展机理上的，其准则不仅考虑了应力、应变的大小，而且还考虑应力、应变所在平面及其方向，被普遍认为是分析多轴疲劳的一种比较有效的方法。

临界平面法主要分两步：第一步，选定疲劳临界面，即疲劳临界面为疲劳裂纹优先萌生和扩展的平面；第二步，计算疲劳临界面上的应力、应变历史，并将其转化成累积的疲劳损伤。选取临界平面首先需要列出构件危险部位处不同位向角平面上的应力/应变时间历程(以受拉扭载荷的薄壁圆管试件为例，图2)，然后再根据不同的准则定义临界平面。确定疲劳裂纹优先萌生和扩展的平面，选取临界平面的准则主要有3种：固定位向角平面、最大正应变准则、最大剪应变准则。

图2 受拉扭载荷的薄壁圆管试件在不同位向角平面上的应变时间历程Fig.2 Strain time course of thin-walled tube specimens with tensile torsional loads at different positions on angular plane

Lohr[29]将结构表面45°位向角平面定义为临界平面，在此平面上定义了等效应变

式中：γ*、ε*为45°位向角平面上的剪应变和正应变；k为材料常数；C为等效应变，对应的一般为修正的Manson-Coffin公式，下同。以固定位向角平面作为临界面虽然操作简单，但其本质仍属于等效应变法，不能准确把握疲劳裂纹萌生和扩展方向，因此应用受到一定的限制。

最大正应力准则主要适用于多轴高周疲劳，其定义最大正应力所在的平面为临界平面。

Smith,Watson和Topper[30]遵照此标准，借鉴能量法的理念，在最大正应力所在的平面上定义了损伤参量，并给出了等效应变模型

寿命预测模型

式中：Δεmax为最大主应变幅；σn,max为最大主应变幅平面上的最大正应力。

最大剪应变准则主要适用于多轴低周疲劳，也是应用最为广泛的一个准则。其中，在多轴疲劳领域，Brown和Miller[31]最早提出的KBW模型就是基于最大剪应变准则，其等效应变模型可表示为

寿命预测模型

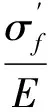
式中：Δγmax为最大剪应变幅；Δεn为最大剪应变幅平面上的最大正应变幅；S为经验参数；υe、υp分别为弹、塑性泊松比。Socie在KBW模型的基础上考虑了平均应力的影响，用平均应力修正了KBW模型

以上几个模型都在定义最大剪应变所在的平面为临界平面的基础上，选取其上的最大正应变计算损伤参量。通过大量实验数据，Shang和Wang[33-35]认为临界面上相邻2个最大剪应变折返点之间的法向应变程更能体现其与寿命之间的关系，并以此为基础提出了著名的Shang-Wang模型

另外，为体现更多材料参数对多轴疲劳性能的影响，Fatemi和Socie[36]引入了最大虚法向应力，以此推导出多轴疲劳寿命表达式

式中：σy为材料屈服极限；σn,max为最大虚法向应力，可表示为

之后，Li[37]考虑了材料附加强化对多轴疲劳寿命的影响，并在此基础上对FS模型进行了进一步的优化，得出等效应变表达式

通过简化，FS模型和Li模型都可写为以下形式

其包含了屈服极限、杨氏模量、应变硬化系数、应变硬化指数等材料参数，更能体现多轴疲劳失效的微观机理，但也需要更多的多轴疲劳试验数据支撑。

2 几类多轴疲劳寿命预测方法分析与比较

第1节介绍了3类多轴疲劳寿命预测方法(等效应变法、能量法、临界面法)。其中等效应变法作为单轴疲劳分析方法的延伸，最早应用于多轴疲劳寿命分析中，在某些场合这一方法简单实用。但通过大量实验数据发现，针对不同加载路径下构件的疲劳寿命，即使等效应变是相同的，但试件试验寿命却相差较大。如图3所示，对于同种材料，在相同等效应变下(分别为0.35%、0.50%、0.70%)，试件的疲劳寿命仍在很大程度上取决于试件加载应变的相位差，大致表现为加载相位差越大，试件疲劳寿命越低。因此，若单纯将等效应变法用于非比例加载下的疲劳寿命估算，将不会给出理想的寿命估算结果。

与其他方法不同，能量法能从疲劳破坏最本质的机理解决疲劳寿命问题，能解释很多其他方法无法解释的疲劳现象。另外，该方法几乎不包含材料参数，应用简单，比较适用于工程应用。但该方法采用能量作为疲劳损伤参数，能量作为一个理论定义通过计算可以得出具体数值，但在试验乃至实际应用过程中，因为构件内部能量会持续不断的与外界发生交流，并有一部分能量会在构件内部发生复杂的理化转化，因此通过现有技术手段很难准确测量构件吸收外部的有效能量，这从根本上限制了能量法的应用。另外，能量作为一个标量，并不能很好的描述加载路径对多轴疲劳寿命的影响，这也在一定程度上限制了能量法模型的准确度。因此，不管在单轴疲劳领域还是多轴疲劳领域，能量法的应用一直受到很大的限制，很难成为主流的寿命预测方法。

图3 文献[38]中实验数据分布举例

临界面法基于多晶体结构金属材料疲劳裂纹成核启裂的观察而发展起来，采用材料最大损伤平面(临界面)上的应力/应变参数作为多轴疲劳损伤控制参量，以此来考虑多轴疲劳破坏面，具有比较明确的物理意义。其可以根据疲劳裂纹的萌生和扩展类型、载荷路径及材料的特性等因素来选择合适的损伤参量，是一种公认的多轴疲劳寿命分析方法，也是现阶段研究最多、应用最广的分析方法。但是，由于受试验测试手段的限制，目前对于临界平面法主要是结合金属材料的圆管薄壁型试件在拉-扭双轴复合加载条件下的疲劳试验进行研究(图4)，缺乏普遍性。另外，因为问题的复杂性，现阶段还没有一种临界平面法模型能全面考虑材料属性对多轴疲劳寿命的影响，对于不同材料，单一的预测模型具有明显的不稳定性。以SHANG-WANG模型、FS模型为例，从文献[31,33,38，41-45]中选取了5中材料的多轴疲劳试验结果进行分析，分别采用SHANG-WANG模型和FS模型计算试件的疲劳寿命，并将得到的结果与相应的实验结果对比(图5)。通过图5可知，两种方法的寿命预测结果都存在很大的分散性。即便如此，临界平面法仍以其他方法无法比拟的优势成为多轴疲劳领域的常用方法，得到了各国学者的普遍关注和认同[39-40]。

图4 拉扭薄壁管件应变状态Fig.4 Strain condition of thin walled pipe under tension and torsion

对于以上提到的3种方法大多是针对的多轴低周疲劳，而针对多轴高周疲劳的研究现阶段还比较少,致使许多多轴高周疲劳寿命问题无法得到准确评估。另外，针对多轴疲劳，现阶段还很少有对材料微结构演化及损伤机理的研究，这也在一定程度上限制了对多轴疲劳附加强化现象的深入探索。因此，鉴于多轴疲劳在工程应用中的普遍性，对于多轴疲劳寿命问题的研究仍任重而道远。

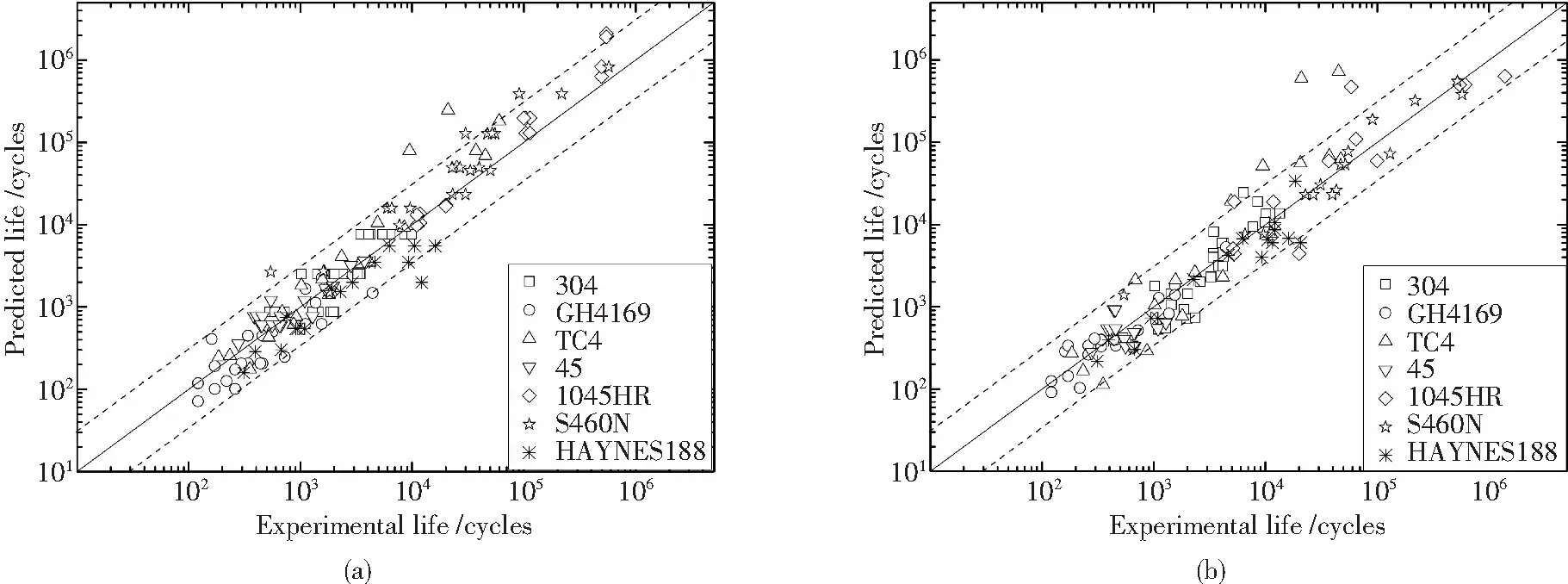
图5 试验寿命与SHANG-WANG模型(a)、FS模型(b)预测值对比Fig.5 Comparison of test life with life predicted by SHANG-WANG model (a) and FS model (b)

3 结论

本文主要对构件在多轴载荷下的寿命预测问题进行了回顾，并就常用的寿命分析方法做了简单分析：

1)等效应变法作为单轴疲劳分析方法的延伸，最早应用于多轴疲劳寿命分析中。在载荷较为简单的场合中，这一方法简单实用，倍受青睐；但针对复杂载荷状况，等效应变法将不能给出理想的寿命估算结果。

2)能量法能从疲劳破坏最本质的机理解决疲劳寿命问题，能解释很多其他方法无法解释的疲劳现象。另外，该方法几乎不包含材料参数，应用简单，比较适用于工程应用。但通过现有技术手段很难准确测量构件吸收外部的有效能量，另外，能量作为一个标量，并不能很好的描述加载路径对多轴疲劳寿命的影响。

3)临界面法不仅考虑了载荷加载过程中应力、应变的大小，而且还考虑应力、应变所在平面及其方向，被普遍认为是分析多轴疲劳的一种比较有效的方法，是一种公认的多轴疲劳寿命分析方法，也是现阶段研究最多、应用最广的分析方法。但是，目前对于临界平面法主要是结合圆管薄壁进行研究的，缺乏普遍性。另外，现阶段也仍未有一种临界平面法模型能全面考虑材料属性对多轴疲劳寿命的影响。即便如此，临界平面法仍以其他方法无法比拟的优势得到了各国学者的普遍认同。

[1] 赵而年,瞿伟廉,周强. 基于临界面损伤参量的金属材料多轴疲劳寿命预测[J]. 华南理工大学学报:自然科学版,2017,45(2):130-136.

[2] 尚德广,王德俊. 多轴疲劳强度[M]. 北京:科学出版社,2007.

[3] Winkler A, Kloosterman G. A critical review of fracture mechanics as a tool for multiaxial fatigue life prediction of plastics[J]. Frattura Ed Integrità Strutturale,2015, 9(33):262-288.

[4] 孙淼,许瑛,李隆. 基于ABAQUS/FE-SAFE的机翼结构多轴疲劳分析[J]. 失效分析与预防,2016,11(1):1-5..

[5] 朱正宇,何国球,张卫华,等. 非比例载荷下多轴疲劳微观机理的研究进展[J]. 同济大学学报:自然科学版,2006,34 (11):1510-1514.

[6] Carpinteri A, Spagnoli A, Vantadori S. A review of multiaxial fatigue criteria for random variable amplitude loads[J]. Fatigue amp; Fracture of Engineering Materials amp; Structures,2017，9(30)：1007-1036.

[7] 刘灵灵,聂辉. 多轴低周非比例加载下疲劳寿命预测方法综述[J]. 华北科技学院学报,2009,6(2):60-63.

[8] Kanazawa K, Miller K J, Brown M W. Low-cycle fatigue under out-of-phase loading conditions[J]. Journal of Engineering Materials amp; Technology,1977,99(3):222.

[9] Socie D. Multiaxial Ffatigue damage models[J]. Key Engineering Materials,1987,324-325(4):747-750.

[10] Zamrik S Y, Ray A, Koss D A. Life prediction of advanced materials for gas turbine application[J]. Office of Scientific amp; Technical Information Technical Reports,1995,12(31):1-20.

[11] Bonacuse P J, Kalluri S. Elevated temperature axial and torsional fatigue behavior of Haynes 188[J]. Journal of Engineering Materials amp; Technology,1995,117(2):191-199.

[12] Itoh T, Sakane M, Ohnami M, et al. Nonproportional low cycle fatigue criterion for type 304 stainless steel[J]. Journal of Engineering Materials amp; Technology,1995,117(3):285-292.

[13] Borodii M V, Strizhalo V A. Analysis of the experimental data on a low cycle fatigue under nonproportional straining[J]. International Journal of Fatigue,2000,22(4):275-282.

[14] Skibicki D,ukasz Pejkowski. Low-cycle multiaxial fatigue behaviour and fatigue life prediction for CuZn37 brass using the stress-strain models[J]. International Journal of Fatigue,2017,102(5):18-36.

[15] Lee S B. A criterion for fully reversed put-of-phase torsion and bending[J]. Astm International in multiaxial Fatigue,1985,22(10):553.

[16] Wang Y Y, Yao W X. Evaluation and comparison of several multiaxial fatigue criteria[J]. International Journal of Fatigue, 2004,26(1):17-25.

[17] Glinka G, Shen G, Plumtree A. A multiaxial fatigue strain energy density parameter related to the critical fracture plane [J]. Fatigue amp; Fracture of Engineering Materials amp; Structures,1995,18(1):37-46.

[18] Sun N N, Li G X, Bai S Z, et al. Study on multiaxial fatigue criterion based on total strain energy[J]. Journal of Ship Mechanics,2015,19(4):405-410.

[19] Böhm M, Niesony A. Strain-based multiaxial fatigue life evaluation using spectral method[J]. Procedia Engineering,2015,101(7):52-60.

[20] Mokhtari H, Esmaeili F, Dabbagh-Yarishah J. Fatigue life estimation of spot-welded joints using several multiaxial fatigue criteria[J]. Transactions of the Indian Institute of Metals,2016,69(8):1-9.

[21] Sonsino. Energy criteria of multiaxial fatigue failure[J]. Fatigue amp; Fracture of Engineering Materials amp; Structures,1999, 22(12):1053-1070.

[22] Ellyin F, Golos K. Multiaxial fatigue damage criterion[J]. Journal of Engineering Materials amp; Technology,1988,110(1):63.

[23] Garud Y S. A New Approach to the evaluation of fatigue under multiaxial loadings[J]. Journal of Engineering Materials amp; Technology Transactions of the Asme,1981,103(2):118-125.

[24] Pan W F, Hung C Y, Chen L L. Fatigue life estimation under multiaxial loadings[J]. International Journal of Fatigue,1999, 21(1):3-10.

[26] Walat K, Kurek M, Ogonowski P, et al. The multiaxial random fatigue criteria based on strain and energy damage parameters on the critical plane for the low-cycle range[J]. International Journal of Fatigue,2012,37(4):100-111.

[27] Berto F, Campagnolo A, Welo T. Local strain energy density to assess the multiaxial fatigue strength of titanium alloys[J]. Frattura Ed Integrità Strutturale,2016,10(37):69-79.

[28] Branco R, Costa J D, Berto F, et al. Fatigue life assessment of notched round bars under multiaxial loading based on the total strain energy density approach[J]. Theoretical amp; Applied Fracture Mechanics,2017,65(5):1127.

[29] Lohr R D, Ellison E G. A simple theory for low cycle multiaxial fatigue [J]. Fatigue amp; Fracture of Engineering Materials amp; Structures,2010,3(1):1-17.

[30] Smith K N, Watson P, Topper T H．A stress-strain function for the fatigue of metals (stress-strain function for metal fatigue including mean stress effect)[J]. Journal of Materials,1970,5(4):767-776．

[31] Kandil F A, Brown M W, Miller K J. Biaxial low cycle fatigue fracture of 316 stainless steel at elevated temperatures[C]//The Metal Society,London,1982,280(2):203-213.

[32] Socie D F, Waill L A, Dittmer D F. Biaxial fatigue of Inconel 718 including mean stress effect[J]. Nutrition Education,1985,5(12):463.

[33] Shang D G, Wang D J. A new multiaxial fatigue damage model based on the critical plane approach[J]. International Journal of Fatigue,1998,20(3):241-245.

[34] Shang D G, Sun G Q, Yan C L, et al. Creep-fatigue life prediction under fully-reversed multiaxial loading at high temperatures[J]. International Journal of Fatigue,2007,29(4):705-712.

[35] Sun G Q, Shang D G. Prediction of fatigue lifetime under multiaxial cyclic loading using finite element analysis[J]. Materials amp; Design,2010,31(1):126-133.

[36] Fatemi A, Socie D F. A critical plane approach to multiaxial fatigue damage including out-of-phase loading[J]. Fatigue amp; Fracture of Engineering Materials amp; Structures,1988,11(3):149-165.

[37] Li J, Zhang Z P, Sun Q, et al. Multiaxial fatigue life prediction for various metallic materials based on the critical plane approach[J]. International Journal of Fatigue,2011,33(2):90-101.

[38] Nitta A, Ogata T, Kuwabara K. Fracture mechanism and life assessment under high-stress biaxial cyclic loading of type 304 stainless steel[J]. Fatigue amp; Fracture of Engineering Materials amp; Structures,2010,12(2):77-92.

[39] Kamal M, Rahman M M. Multiaxial fatigue life modelling using hybrid approach of critical plane and genetic algorithm[J]. Fatigue amp; Fracture of Engineering Materials amp; Structures,2016,39(4):479-490.

[40] Palin-Luc T, Morel F. Critical plane concept and energy approach in multiaxial fatigue[J]. Materialprufung,2016,47(5):278-286.

[41] Launay A, Maitournam M H, Marco Y, et al. Multiaxial fatigue models for short glass fibre reinforced polyamide. Part II: Fatigue life estimation[J]. International Journal of Fatigue,2013,47(1):390-406.

[42] Lohr R D, Ellison E G. A simple theory for low cycle multiaxial fatigue[J]. Fatigue amp; Fracture of Engineering Materials amp; Structures,1980,3(1):1-17.

[43] Gerin B, Pessard E, Morel F, et al. Beneficial effect of prestrain due to cold extrusion on the multiaxial fatigue strength of a 27MnCr5 steel[J]. International Journal of Fatigue,2016,92:345-359.

[44] Chen X, Gao Q, Sun X F. Low-cycle fatigue under non-proporational loading [J]. Fatigue amp; Fracture of Engineering Materials amp; Structures,1996,19(7):839-854.

[45] Itoh T, Sakane M, Hata T, et al. A design procedure for assessing low cycle fatigue life under proportional and non-proportional loading[J]. International Journal of Fatigue,2006,28(5):459-466.

Summarizationofmulti-axialfatiguelifepredictionmethods

ZHAO Bing-feng1, XIE Li-yang1, XU Guo-liang2, LI Hai-yang1, ZHANG Shi-jian1, WANG Bo-wen1

(1.KeyLaboratoryofVibrationandControlofAeronauticalPowerEquipment,NortheasternUniversity,Shenyang110819,China;2.ChinaAerospaceScienceandTechnologyGroup702ResearchInstitute,Beijing100076,China)

In engineering practice, most engineering structures and mechanical parts are subjected to various forms of cyclic loads, and most of the load distributions exhibit multiple axial stress states. Under cyclic load, the study of multi-axis fatigue life is more close to engineering practice than that of uniaxial fatigue and has a wider application background. As for this situation, the research state of multi-axis fatigue life prediction methods in recent years was described in detail. The fundamentals, advantages and disadvantages of three major methods were introduced and compared: equivalent strain method, energy method and critical plane method. In addition, in view of the shortcomings of various multi-axial fatigue life methods at present, the future research work in multi-axial fatigue field was put forward.

multi-axial fatigue; life prediction; equivalent strain method; energy method; critical plane method

2017年9月5日

2017年10月15日

国家自然科学基金重点项目“航空发动机结构可靠性多元建模及仿真理论与方法研究”(02090074113015)；辽宁重大装备制造协同创新中心(03220075115001)

赵丙峰(1991年-)，男，博士，主要从事多轴疲劳、疲劳可靠性等方面的研究。

TH114; O346.2

A

10.3969/j.issn.1673-6214.2017.05.012

1673-6214(2017)05-0323-08