一类具有双线性发生率分数阶SIS传染病模型的全局稳定性

郑义,杨霞*

（石河子大学理学院数学系，新疆 石河子 832003）

一类具有双线性发生率分数阶SIS传染病模型的全局稳定性

郑义,杨霞*

（石河子大学理学院数学系，新疆 石河子 832003）

本文研究了一类分数阶SIS传染病模型的全局稳定性问题，得到了模型的无病平衡点E0与有病平衡点E*，分别通过构造相应的Lyapunov函数对平衡点的全局稳定性进行讨论，得到结论：当R0＜1时模型，模型只存在无病平衡点E0，无病平衡点E0在区域D内是全局渐进稳定的；当R0＞1时模型存在无病平衡点E0以及地方病平衡点E*，地方病平衡点E*在区域D内是全局渐进稳定的。最后通过数值模拟及对比验证所得结论，并给出控制疾病流行的一些可行性意见。

平衡点；全局稳定性；分数阶动力系统；Lyapunov函数；双线性发生率

数学模型可以用于描述流行病的传播，对疾病的预防以及控制起着重要的作用。在传染病动力学中，主要采用的是由Kermack与McKendrick在1927年所建立的SIS和SIR仓室模型[1]。随着数学理论的发展，经典模型得到了不断的变化与改进[2-3]。近年研究人员发现分数阶微积分与分形几何、记忆过程有密切的联系。分数阶微积分被广泛应用到生物数学，物理学，工程科学等一些领域[4-6]。随着分数阶微积分被引入传染病动力学中，依据分数阶微积分所建立的模型具有整数阶所不具备的性质[7]。原三领等[8]讨论了一类双线性发生率的分数阶模SIR型，赵洪勇等[9]研究了一类具有免疫的分数阶HIV模型。然而，分数阶传染病模型的全局稳定性问题还没有得到很好地解决，因此，本文通过Lyapunov构造函数来证明平衡点的全局稳定性，给出了一种判断流行病模型平衡点全局稳定性的一种方法。

本文探讨具有双线性发生率的分数阶SIS流行病模型，对模型进行分析得到模型的平衡点与阈值，讨论平衡点的全局稳定性。通过理论分析，得到区分疾病是否在该地区的判断依据阈值R0；再对阈值分析，在理论上给出控制疾病流行的一些相应的方案；对模型进行数值模拟来验证理论分析的合理性；通过不同阶的分数阶模型的对比来发现之间的差异，并对这些结果进行分析。

1 模型引入

假设某一地区在时刻t的总人口数为N(t)，包括易感者、已感者2类，这2类人口数分别记为S(t)、I(t)，设A为进入该地区的总人口数，进入该地区的人口都将作为易感者。具有双线性发生率的SIS传染病模型如下：

式中：βSI为染病者的双线性发生率，μ为自然死亡率，α为因病死亡率，δ为恢复率系数，假设参数A、β、μ、δ、α都是正数，并分别具有实际意义。

下面给出分数阶微积分的定义[11]。本文中采用的是Caputo型的分数阶导数。

定义1：函数f:R+→R的α＞0阶分数阶Caputo型导数的定义为

通过Caputo型分数阶的定义，分数阶动力系统的定义为

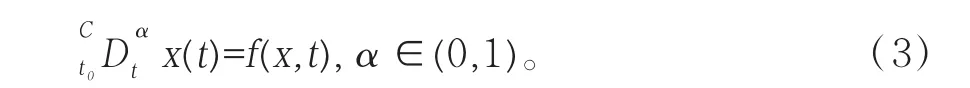
定义2：x0是分数阶系统（3）的平衡点，当且仅当f(x,t0)=0。

本文研究模型如下

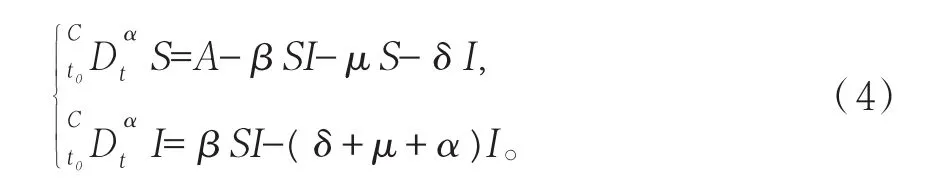
由模型（4）知

根据方程（5）易知，当疾病不存在时总人口N(t)数最终趋于，因此模型（5）的全部解将进入或停留在区域D中，其中

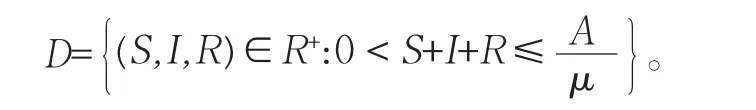
区域D是模型（5）的正不变集，故定义基本再生数为

2 平衡点的全局稳定性

引理1(Lasalle不变原理)[9]：假设D是一个有界闭集,每个的解从D内的一点出发最终仍在D内，如果存在V(x):D→R连续偏导数满足下面条件：

引理 2[12]：若x(t)∈R是连续可导函数，则对于任意的t≥t0都有

引理 3[12]：若x(t)∈R是连续可导函数，则对于任意的t≥t0都有

引理4（一致渐近稳定性定理）[13]：若x*是分数阶动力系统的平衡点，Ω∈Rn是一个包含x*的区域。若L(t,x(t)):[0,∞]×Ω→R是连续可微函数满足如下条件

定理1：当R0＜1时模型（4）存在无病平衡点E0(S0,I0)，无病平衡点E0在区域D内是全局渐进稳定的，

证明：构造如下Lyapunov函数

根据引理2对V(S,I)求导得

将A=μS0代入上式

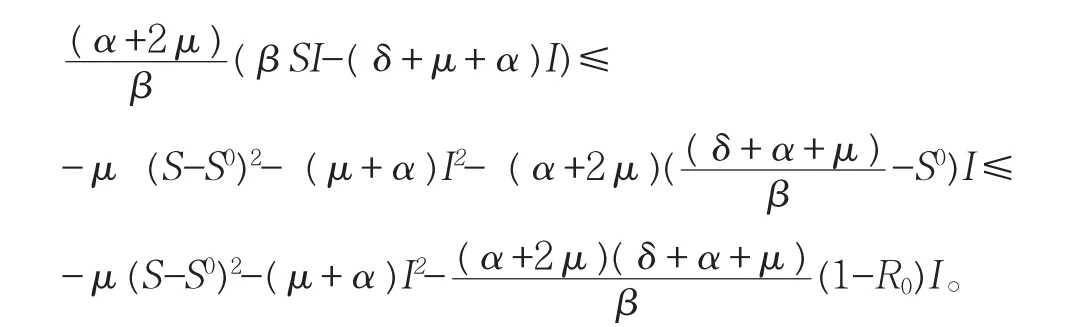
当R0＜1 时当且仅当S=S0,I=0时

定理2：当R0＞1时模型（4）存在无病平衡点E0以及地方病平衡点E*(S*,I*)，地方病平衡点E*在区域D内是全局渐进稳定的，

证明:构造如下Lyapunov函数

根据引理2和引理3对V(S,I)求导得

将A=μ(S*+I*)-αI*，βS*=(δ+μ+α)代入上式得

当R0＞1 时，。当且仅当S=S*,I-I*时

3 数值模拟与分析

（1）当R0＜1时模型（4）存在无病平衡点，并且无病平衡点是全局渐进稳定的。

选取α=0.8，初始值（S0,I0）=(5,2)，A=1，β=0.2，μ=0.4,α=0.4,δ=0.2。通过计算可得R0=0.5＜1，无病平衡点E0(S0,I0)=(2,5,0)，模型（4）的易感者、感染者人数变化情况如图1所示。

（2）当R0＞1时模型（4）存在无病平衡点与地方病平衡点，并且地方病平衡点是全局渐进稳定的。

图1 R0＜1时易感者、感染者人数变化图

选取α=0.8，初始值（S0,I0）=(5,2)，A=2，β=0.2，μ=0.2,α=0.4,δ=0.2。通过计算可得R0=2.5＞1，无病平衡点E*(S*,I*)=(4,2)。模型（4）的易感者、感染者人数变化情况如图2所示。

图2 R0＞1时易感者、感染者人数变化图

4 模型对比与分析

对于整数阶动力系统模型与分数阶系统模型的差异性，分别对不同数值α的模型进行对比。对于模型（4），分别取α=0.6,0.8,1，时，通过计算来进行比较。

R0＜1 时，初始值 （S0,I0）=(5,2)，A=1，β=0.2，μ=0.4,α=0.4,δ=0.2。通过计算可得R0=0.5＜1，无病平衡点E0(S0,I0)=(2,5,0)，模型（4）的易感者、感染者人数变化情况如图3、4所示。

R0＞1 时，初始值 （S0,I0）=(5,2)，A=2，β=0.2，μ=0.2,α=0.4,δ=0.2。通过计算可得R0=2.5＞1，无病平衡点E*(S*,I*)=(4,2)。模型（4）的易感者、感染者人数变化情况见图5、6。

图3 R0＜1时易感者人数变化

图4 R0＜1时感染者人数变化

图5 R0＞1时3种模型易感者人数变化

图6 R0＞1时3种模型感染者人数变化

对上述数值模拟结果分析可知：

（1）不同分数阶传染病模型不仅与相对应的整数阶模型具有相同的平衡点，而且平衡点的稳定性性质也保持一致。

（2）不同阶模型在数量的变化上互有区别，对于疾病的模型建立，我们可以选取适当分数阶模型来描述疾病的流行过程。

5 结语

（1）本文研究了一类具有标准发生率分数阶SIS流行病模型的全局稳定性，得出判断疾病的阈值R0，当R0＜1时模型，模型只存在无病平衡点E0，无病平衡点E0在区域D内是全局渐进稳定的，疾病最终会在该地区最终灭绝不会流行；当R0＞1时模型存在无病平衡点E0以及地方病平衡点E*，地方病平衡点E*在区域D内是全局渐进稳定的，表明感染者人数最终会在该地区达到一个稳定的数量，即疾病会在该地区形成地方病。上述结果可为控制疾病的流行提供理论依据；在实际情况中，应采取适当的措施尽量减少R0的值，如减少接触率（即减小β）、增大治愈率（即增大δ）等一系列措施来控制疾病流行。

（2）数值模拟分析结果表明：整数阶模型与分数阶模型具有相同的稳定性。这有助于分析模型平衡点的稳定性，也有助于研究更复杂分数阶流行病模型的动力学性质。

（3）通过不同阶模型之间的对比发现：不同阶模型在变化的过程中有所区别。这表明在模型建立中可以选取适当阶数的模型来描述疾病的流行过程。

[1]马知恩.传染病动力学的数学建模与研究[M].北京：科学出版社,2004:126-127.

[2]殷红燕,宁娣,周静.一类具时滞的病毒模型的稳定性与Hopf分支[J].中南民族大学学报(自然科学版),2015,34(1):117-121.Yin Hongyan,Ning Di,Zhou Jing.Stability and Hopf Bifurcation for a Class of Viral Model with Delay[J].Journal of South-Central University for Nationalities(Natural Science Edition),2015,34(1):117-121.

[3]殷红燕,蒋翔.一类带有不育蚊子的疟疾传播模型的分析[J].中南民族大学学报(自然科学版),2016,35(4):137-141.Yin Hongyan,Jiang Xiang.Analysis of a Malaria Transmission Model with Sterile Mosquitoes[J].Journal of South-Central University for Nationalities(Natural Science Edition),2016,35(4):137-141.

[4]E Ahmed,A M A El-Sayed,H A A.El-Saka.Equilibrium points,stabilityand numericalsolutionsoffractional-order predator–prey and rabies models[J].J Math Anal Appl,2007,325:542-553.

[5]Li Y,Chen Y,Podlubny I.Stability of fractional-order nonlinear dynamic systems:Lyapunov direct method and generalized Mittag-Leffler stability[J].Comput Math Appl，2010，59:1810-1821.

[6]Pourmahmood M.Robust stabilization and synchronization of a class of fractional-order chaotic systems via a novel fractional sliding mode controller[J].Commun Nonlinear Sci Numer Simul,2012;17:2670–2681.

[7]T J Anastasio.The Fractional-order Dynamics of Bainstem Vestibule-oculomotorNeurons [J].BiologicalCybernetics，1994，72:69-79．

[8]原三领,李小月,许超群.一类分数阶SIR流行病模型的稳定性研究[J].生物数学学报，2016,31（1）：71-82.Yuan Sanling,Li Xiaoyue,Xu Chaoqun.Study on the stability of a kind of fractional order SIR epidemic model[J].Journal of Biomathematics,2016,31(1）：71-82.

[9]Huo J,Zhao H,Zhu L.The effect of vaccines on backward bifurcation in a fractional order HIV model[J].Nonlinear Anal-Real,2015,26:289-305.

[10]Song X,Neumann A U.Global stability and periodic solution of the viral dynamics[J].J Math Anal Appl,2007,329(1):281-297.

[11]IPodlubny.FractionalDifferentialEquations[M].London:Academic Press，1999:78-81.

[12]Vargas-De-León C.Volterra-type Lyapunov functions for fractional-orderepidemic systems[J].Communicationsin Nonlinear Science and Numerical Simulation,2015,24(1):75-85.

[13]H Delavari,D Baleanu,J Sadati.Stability analysis of Caputo fractional-order nonlinear systems revisited[J].Nonlinear Dyn 2012,67:2433-2439.

Global stability of a fractional-order SIS epidemic model with bilinear incidence rate

Zheng Yi,Yang Xia*
(Department of Mathematics,School of Science,Shihezi University,Xinjiang,Shihezi 832003,China)

In this paper,we discussed the global stability of a class of a fractional-order SIS epidemic model.By calculating,we obtained the disease-free EquilibriumE0and endemic equilibriumE*.By constructing the Lyapunov function,we obtain the global stability of the equilibrium points.WhenR0＜1,the disease-free equilibrium pointE0is globally asymptotically stable;whenR0＞1,the endemic equilibrium pointE*is globally asymptotically stable.Finally,some numerical simulations are given to confirm the conclusions.Some feasible suggestions are given to control the spread of disease.

equilibrium point;global stability;fractional dynamic system;Lyapunov function;bilinear incidence rate

Q332

A

10.13880/j.cnki.65-1174/n.2017.05.022

1007-7383(2017)05-0652-05

2016-12-12

郑义（1991-）,男，硕士研究生，专业方向为生物数学。

*通信作者：杨霞（1968-），女，教授，从事微分动力系统方向研究，e-mail：xyshzu@163.com。