一种基于AR运动模型CKF算法的无人机导航

孙 蕊，程 琦，张羽成，王冠宇

(南京航空航天大学 民航学院，江苏 南京 211106)

引用著录：孙蕊，程琦，张羽成，等.一种基于AR运动模型CKF算法的无人机导航[J].测绘工程，2017，26(12)：41-44，49.

DOI:10.19349/j.cnki.issn1006-7949.2017.12.008

一种基于AR运动模型CKF算法的无人机导航

孙 蕊，程 琦，张羽成，王冠宇

(南京航空航天大学 民航学院，江苏 南京 211106)

针对无人机组合导航滤波算法中传统的运动模型单一固定，灵活性差，无法精确描述无人机复杂多变的运动状态，甚至还会导致滤波发散等问题，提出了一种基于AR运动模型的CKF算法，并应用于无人机导航定位中。通过滑动窗的方法，构建实时动态更新AR模型估计物体运动状态，并且结合CKF进行滤波，从而有效提高无人机导航性能。仿真实验结果表明，该算法能够有效提高无人机导航定位精度，优于其余几种基于传统运动模型的滤波算法。

无人机；导航；滤波算法；自回归模型；GPS

精确导航定位技术是无人机实现安全飞行的基础。全球定位系统(Global Positioning System, GPS)和惯性导航系统(Inertial Navigation System, INS)可以实时获取无人机的位置和姿态信息，目前在无人机导航中被广泛应用。GPS/INS通过滤波算法进行组合，可以有效提高无人机导航性能。滤波算法可以对GPS与INS数据进行估计、修正、融合，对两个系统进行取长补短，来解决GPS信号失锁引起的无法定位问题和INS长时间积累误差引起的漂移问题，因此在无人机组合导航中具有非常重要的作用。目前，无人机导航大多采用非线性滤波。早期的扩展卡尔曼滤波 (Extended Kalman Filter, EKF)通过对非线性函数进行Taylor级数展开，从而实现线性化解算。但是其精度只停留在一阶，尤其在无人机高动态系统的导航中误差较大[1-2]。无迹卡尔曼滤波(Unscented Kalman filter, UKF)通过经无迹变换后的采样点集来逼近非线性函数概率分布，因此不需要计算非线性系统的雅可比矩阵，相比EKF具有更好的非线性估计性能[3]。粒子滤波(Particle filter，PF)是一种基于蒙特卡洛仿真的滤波，它通过粒子分布来逼近系统的后验概率，理论上只要粒子数目足够多，就可以实现任意估计精度。然而PF随着粒子数目增多而导致计算量增大，因此难以满足无人机实际导航应用中的实时性需求[4]。

为了更好地满足无人机的导航需求，有必要研究精度更高、更易工程实现的方法。容积卡尔曼滤波(Cubature Kalman filter , CKF)是近年来提出的一种新型非线性高斯滤波方法。CKF具有严格的数学证明，通过三阶容积法则的数值积分方法来近似高斯加权积分，充分利用了容积积分近似计算多维函数积分，具有效率高的特点。经证明其对随机变量非线性变换后概率分布具有良好的逼近精度。相比于EKF、UKF和PF等非线性滤波算法，CKF算法的计算结果对系统状态的估计更加精确，更能有效逼近非线性系统的真实状态，输出结果也更稳定，而且实现简单，能够达到三阶精度[5]。

在滤波算法中，无人机的运动模型通过对短时间内其所遵循的规律来预测下一个时刻的状态，对实现高性能的估计至关重要。实际情况中运动载体一般难以确保规则运动, 因而构造精确的函数模型十分困难[6]。如果其不能精准地表征物体实际运动状态，就会导致滤波器估计精度下降甚至发散[7-9]。关于运动模型的构建，国内外学者都做了相应的研究，并且应用到多个领域。传统运动模型的研究包括：匀速(Constant Velocity, CV)模型、匀加速(Constant Acceleration , CA)模型、恒定转向角的匀速(Constant Turn Rate and Velocity, CTRV)模型、恒定转向角的匀加速(Constant Turn Rate and Acceleration, CTRA)模型、恒定曲率和加速度(Constant Curvature and Acceleration, CCA)模型等[10-11]。然而这些传统模型单一固定，灵活性差，无法精确地描述出无人机复杂多变的运动状态。为了克服这一缺点，近几年来,基于实时动态的运动特征来构建运动模型的研究逐渐兴起。Zhou 和 Li针对全球导航卫星系统(Global Navigation Satellite System, GNSS)导航中传统运动模型只考虑前一时刻状态信息的问题，提出基于滑动窗口和多项式拟合的实时动态运动模型，该方法可以从多个历史时段中得到更多信息，从而提高了导航系统的准确性和可靠性[12]。Lan等提出了一种多模态运动模型并行自适应估计算法，该算法在描述和处理复杂的运动过程时具有较强的灵活性[13]。Jin等提出了基于最小均方根误差优化的自回归运动状态预测模型，该模型比基于传统运动模型的卡尔曼滤波方法得到的精度更高[14]。在地面车辆的位置和运动状态估计中，这些新型的运动模型确实在一定程度上展现了他们的优势。但是，传统的车辆运动模型都是基于二维平面，而无人机的运动是在三维空间中，含有更多的变量、同时环境也更为复杂。现有的运动模型依然无法精确的描述无人机的运动状况。

针对以上问题，本文提出了一种基于自回归(Auto Regressive, AR)运动模型的CKF算法并且运用于无人机导航中。文章通过滑动窗的方法，构建实时动态更新的AR运动模型，对无人机的运动状态进行预测，从而有效提高无人机的导航性能。最后，通过在仿真实验中和其余几种基于传统运动模型的CKF算法进行比较，证明了设计算法的有效性。

1 AR运动模型的构建

传统的离散时间差分模型可以描绘物体运动，但它们一旦建立就不会变化，不能自适应地随着过程噪声和测量噪声强度去调整，自然会在一定程度上导致性能降低。针对该问题，本文用AR模型来描述无人机的运动状态。AR 模型的原理是：通过对一组已有的历史数据进行线性组合，给出关心时刻的预测信息[15],即根据p个历史数据信息，推出第p时刻前面或后面的数据。其本质与插值法类似，两者都是增加有效数据，不同的是AR模型是由p点递推，而插值是由两点(或少数几点)去推导多点，所以AR模型要比插值方法效果更好。

历史数据Xt,白噪声序列表示为at,回归系数用φj(j=1,2,..p)表示，则可得到AR模型：

Xi+1=φ1Xt+φ2Xt-1+φ3Xt-2+…+φpXt-p+1+at.

(1)

2 基于AR模型的CKF算法(CKF-AR)

在非线性系统中，一般动态模型是离散时间运动模型，形式如下：

xk+1=Fk+1|kxk+wk.

(2)

式中：xk表示k时刻的状态向量；Fk+1|k是状态转移矩阵；过程噪声wk为零均值高斯随机过程；其协方差矩阵为Qk。

k时刻观测方程如下：

zk=Hxk+vk.

(3)

式中：zk是系统的量测值；H为测量矩阵；测量噪声vk是零均值高斯随机过程，独立于wk,其协方差矩阵为Rk。

在本文算法中，选取系统的状态向量为xk=[Ek,Nk,Uk,VEk,VNk,VUk,θEk,θNk,θUk]T。其中Ek,Nk,Uk分别是无人机在当地坐标系中的东向、北向和高度坐标；VEk,VNk,VUk分别是无人机在东向、北向和垂直方向上的速度；θEk,θNk,θUk为无人机的姿态角。在构建CKF-AR算法时，需要解决一个问题。即在传统的滤波算法的状态转移方程中第k时刻的状态仅与上一时刻状态有关，而在AR模型中，第k时刻的状态与前p个时刻状态有关。针对该问题，本文算法创新之处在于先由AR模型预测出xk，然后构造出如下关系式：

(4)

xEk=[EkEk-1Ek-2…Ek-p+1]T.

(5)

Ek+1=φEkxEk+aEk.

(6)

式中：φEk是Ek的回归系数；xEk是前p个历史数据；aEk是k时刻Ek的白噪声，这样就得到了k+1时刻的预测值。Nk,Uk,VEk,VNk,VUk,θEk,θNk,θUk的计算过程类似，这里不再赘述。CKF-AR算法步骤如下：

1)获得一组采样点及其对应权值。

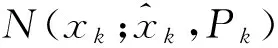
n.

(7)

每个粒子对应权值：

(8)

式中：n是维度。

2)计算容积点集的一步预测，i=1，2

(9)

3)计算系统状态量的一步预测及协方差矩阵，一步预测由容积点集的预测加权求和得到。

(10)

(11)

4)根据一步预测值，对P(k+1|k)做Cholesky分解，产生新的容积点集。

(12)

(13)

5)将由4)预测的容积点集代入观测方程，得到预测的观测量，i=1，2…2n。

(14)

6)由5)得到容积点集的预测观测值，通过加权求和得到系统预测值、k+1时刻量测误差协方差阵及k+1时刻一步预测互相关协方差阵。

(15)

(16)

(17)

7)计算Kalman增益矩阵。

(18)

8)最后，计算系统的状态更新和协方差更新。

(19)

(20)

令k为k+ 1，并返回步骤1。

3 实验和分析

本实验利用Matlab随机模拟一段不规则无人机飞行轨迹，如图1所示。在整个期间,无人机均以变化的速度飞行。采样频率为10 Hz，共采样1 200个点，对应的东、北、高方向上的坐标为(E，N，U)、连接这些样本点的曲线作为参考轨迹。同时利用仿真软件生成3组1 200个满足均值为0，方差为1的正态分布散点w1、w2、w3作为误差。对应地用(E(i)+w1(i),N(i)+w2(i),U(i)+w3(i))作为GPS的观测数据。实验设定观测噪声和过程噪声都是均值为0、方差为1的高斯白噪声。

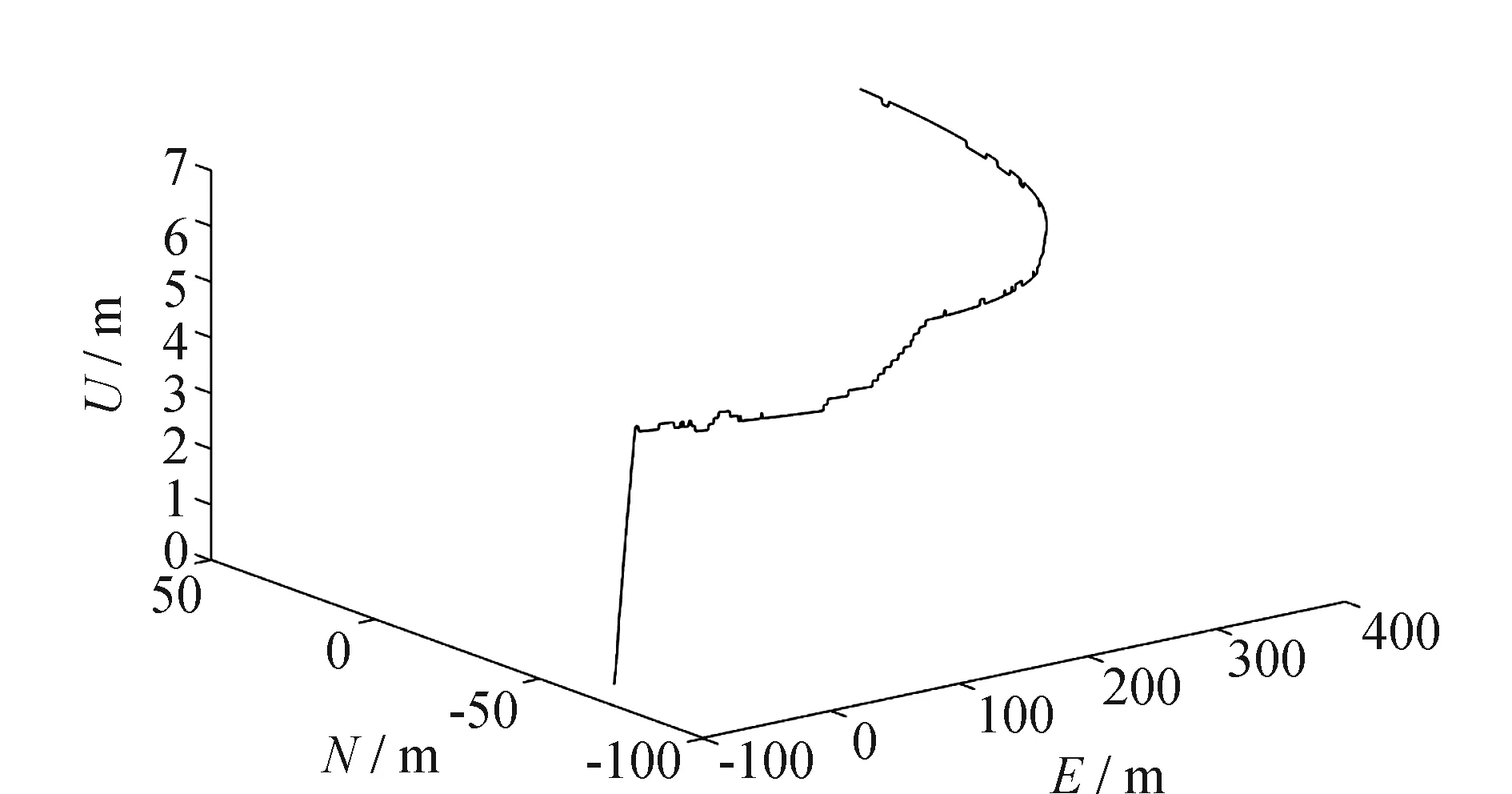
图1 飞行轨迹

本次仿真主要观测信息为无人机的位置坐标，比较本文算法与基于CV模型的CKF算法(CKF-CV)和基于CA模型的CKF算法(CKF-CA)在东、北、高方向上的滤波效果，比较整个飞行过程中定位精度；然后分别计算上述滤波模型及观测数据的均方根误差(Root Mean Square Error, RMSE)，通过均方根误差的大小来评价上述各方案的表现。均方根误差对一组测量中的特大或特小误差反映非常敏感，所以，均方根误差能够很好地反映出测量的精密度。RMSE计算公式如下：

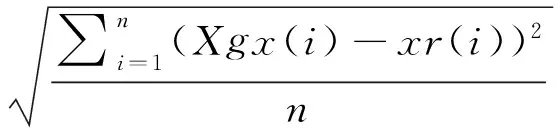
(21)

式中：Xgx(i)为被评价的值，即滤波后的值或观测值；xr(i)为真值，n为观测次数

图2显示了CKF-AR、CKF-CA和CKF-CV算法在东、北、高方向上的滤波结果，表1计算了各算法的均方根误差。

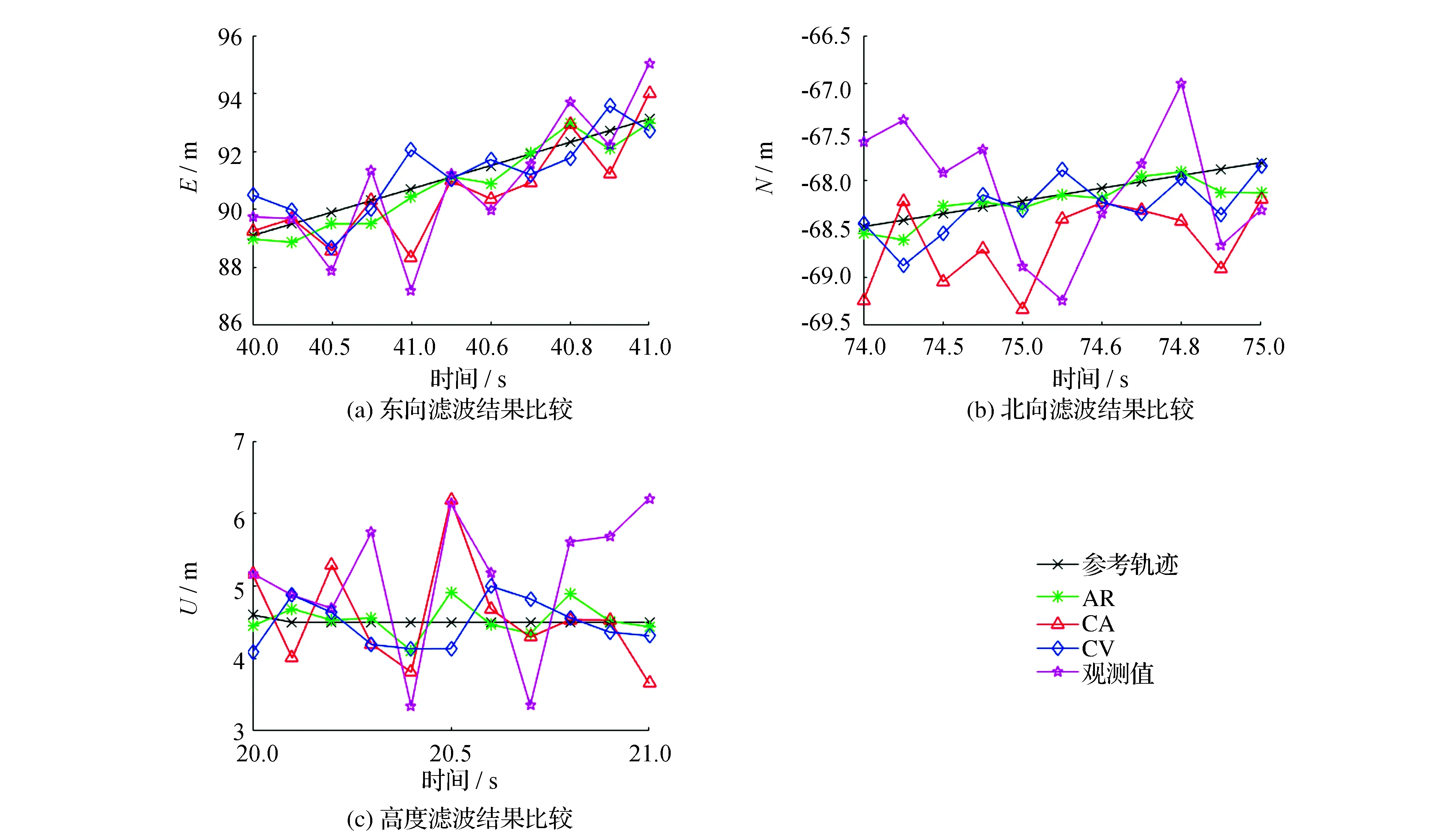
图2 各个方向滤波结果对比

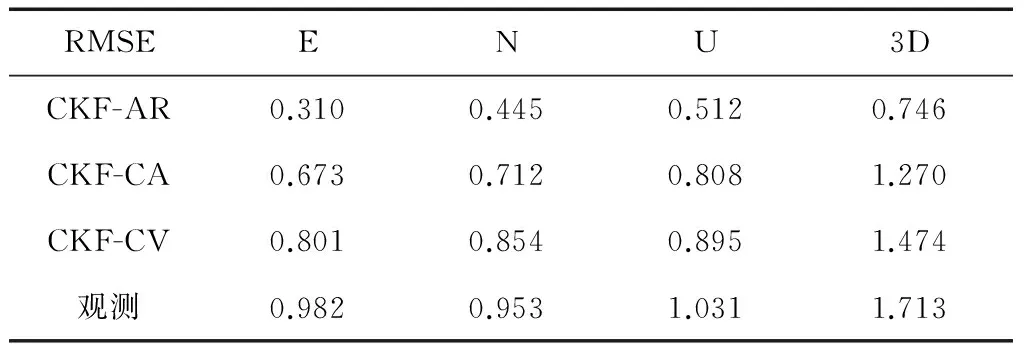
根据图2和表1的结果,得出结论如下：

1)在整个仿真运动过程中，飞行轨迹有直线也有曲线，飞行过程随机性和不规则性极强。CKF-AR算法具有非常明显的效果，定位精度提高了55.4%，而对应的CKF-CA及CKF-CV分别提高了25.9%和14.0%。这表明本文所设计的算法可以充分描述无人机不规则运动的特征，大大提高了定位精度。

2)在整个仿真运动过程中，无人机均是以变化的速度及变化的加速度飞行，这表明CKF-AR算法对无人机的运动类型没有限制，在无人机导航定位中可以适应无人机多种类型的飞行行为。

4 结束语

本文构建了一种基于AR运动模型的CKF自适应滤波算法并运用于无人机导航，并且在和基于传统的运动模型滤波算法比较中，获得了较好的估计精度。实验证明，不管无人机是在直线还是曲线的运动情况下，CKF-AR算法都具有比较好的定位精度，并且在运动模型的构建中，不需要速度、加速度等一系列其他的运动特征，可以实现实时快速运动模型的构建。在今后的研究中，将在多个场景中采集真实数据，从而进一步对所设计的算法进行验证。

[1] LIU G, LI Q, SHI W, et al. Application of dynamic Kalman filtering in state estimation of navigation test[J]. Chinese Journal of Scientific Instrument, 2009, 30(2):396-400.

[2] WANG J. Research of algorithm for mobile node localization in mine based on Kalman filtering[J]. Journal of Electronic Measurement & Instrument, 2013.

[3] Hu, G., Gao, S., & Zhong, Y. A derivative UKF for tightly coupled INS/GPS integrated navigation.[J]. Isa Transactions, 2015: 135-144.

[4] Carmi A, Oshman Y. Fast Particle Filtering for Attitude and Angular-Rate Estimation from Vector Observations[J]. Journal of Guidance Control & Dynamics, 2015, 32(1):70-78.

[5] JIA B, XIN M, CHENG Y. High-degree cubature Kalman filter[J]. Automatica, 2013, 49(2):510-518.

[6] 高为广,张双成,王飞,等. GPS导航中的抗差自适应Kalman滤波算法[J]. 测绘科学, 2005, 30(2):98-100.

[7] JWO D, WANG S. Adaptive fuzzy strong tracking extended Kalman filtering for GPS navigation[J]. IEEE Sensors Journal, 2007, 7(5): 778-789.

[8] 李勇军, 左娟. GPS动态定位自适应卡尔曼滤波算法研究[J]. 测绘工程, 2012, 21(4):29-32.

[9] 杨元喜, 唐颖哲, 李庆田,等. 用于GIS道路信息修测的动态GPS自适应滤波试验[J]. 测绘科学, 2003, 28(4):9-11.

[10] BAR-SHALOM Y, Li X, KIRUBARAJAN T. Estimation with applications to tracking and navigation: theory algorithms and software[M]. Wiley: Hoboken, 2001, 53 (6): 993-999.

[11] SCHUBERT R, RICHTER E, WANIELIK G. Comparison and evaluation of advanced motion models for vehicle tracking[C]// International Conference on Information Fusion. IEEE, 2008:1-6.

[12] ZHOU Z, LI B. GNSS windowing navigation with adaptively constructed dynamic model[J]. GPS Solutions, 2015, 19(1):37-48.

[13] LAN J, LI X R. Equivalent-model augmentation for variable-structure multiple-model estimation[J]. IEEE Transactions on Aerospace and Electronic Systems, 2013, 49(4): 2615-2630.

[14] JIN B, GUO J, He D, et al. Adaptive Kalman filtering based on optimal autoregressive predictive model[J]. GPS Solutions, 2017, 21(2):1-11.

[15] 齐泉林, 宋科璞, 朱雪耀. 基于卡尔曼滤波的AR模型无人自主空中加油预测制导策略[J]. 兵工自动化, 2016, 35(10):55-59.

[责任编辑：王文福]

ACKF-ARalgorithmbasedUAVnavigation

SUN Rui, CHENG Qi, ZHANG Yucheng,WANG Guanyu

(College of Civil Aviation,Nanjing University of Aeronautics and Astronautics,Nanjing211106, China)

Filtering algorithms have been widely used in GPS/INS integration based UAV navigation. The motion model, as the key component in the filter prediction, is critical for the algorithm performance. However, the traditional motion model only uses a fixed motion mode for the prediction, which is not able to describe the UAV motion accurately. In this paper, an AR motion model based CKF algorithm for the UAV state estimation is proposed. By constructing the real-time dynamic updating AR model with sliding window, the adaptive filtering is designed for the UAV states estimation. The simulation results show that the positioning estimations from the designed CKF-AR based filtering algorithm are superior than the other traditional motion model based filtering results.

UAV; navigation;filtering algorithm;AR model;GPS

P237

A

1006-7949(2017)12-0041-04

2017-04-20

国家自然科学基金(41704022)；江苏省自然科学基金(BK20170780)；中央高校基本科研业务费专项资金(NJ20160015； NS2017043)

孙 蕊(1984-)，女，博士.