基于GPS的MODIS近红外可降水量季节性模型建立

段茜茜，曲建光，高 伟，王帅民

(1.天津城建大学 地质与测绘学院，天津 300384；2.黑龙江工程学院 测绘工程学院，黑龙江 哈尔滨 150050)

引用著录：段茜茜，曲建光，高伟，等.基于GPS的MODIS近红外可降水量季节性模型建立[J].测绘工程，2017，26(12)：21-27.

DOI:10.19349/j.cnki.issn1006-7949.2017.12.004

基于GPS的MODIS近红外可降水量季节性模型建立

段茜茜1，曲建光2，高 伟1，王帅民1

(1.天津城建大学 地质与测绘学院，天津 300384；2.黑龙江工程学院 测绘工程学院，黑龙江 哈尔滨 150050)

在考虑可降水量季节性变化的基础上，提出利用GPS数据建立MODIS近红外可降水量季节性模型。首先对比分析2014年北京房山(BJFS)站的GPS可降水量和相应时间的MODIS近红外可降水量数据，发现两者之间的变化趋势基本一致，存在显著线性相关性；然后以GPS可降水量为标准值，利用回归分析建立GPS和MODIS可降水量之间的季节和全年校正模型。经检验，GPS可降水量与四个季节模型校正的MODIS近红外可降水量的均方根误差均小于3 mm，最大误差不超过6 mm，季节校正模型的精度都要高于全年校正模型。

GPS；可降水量；MODIS；校正；季节模型

精确的可降水量(precipitable water vapor, PWV)反演及其时空变化情况在降水预报、全球气候变化研究和InSAR大气校正中有重要的研究意义[1-3]。卫星遥感和GPS反演是获取大气可降水量的重要手段[4-5]。MODIS可降水量数据(以下简称MODIS_PWV)具有尺度大、空间分布连续的优势，但精度不理想[6]。GPS反演可降水量(以下简称GPS_PWV)有快速、精确、时间分辨率高以及不受天气影响等优势，但是由于地基GPS站点密度的限制，很难反映详细的空间水汽变化情况[7]，因此综合两者优势，利用GPS_PWV校正MODIS_PWV具有重要的研究价值。目前，关于GPS_PWV和MODIS_PWV的相关性和模型建立的研究成果有很多，当前研究仅基于短期数据进行相关性分析并建立模型[8-9]或者基于长期数据只建立一个单一的模型[10-12]，模型精度比较低。

综上所述，发现以往研究中缺少对不同季节GPS_PWV和MODIS_PWV的相关性分析、季节校正模型的建立。由于可降水量随季节的变化较大，因此有必要建立GPS_PWV校正MODIS_PWV的季节模型。本文在考虑可降水量季节性变化的基础上，以BJFS站2014年的GPS_PWV和MODIS_PWV展开相关性分析，建立线性回归模型，并用2015年的数据进行模型的检验。

1 数据的获取

在美国国家航空航天局的网站可获取全球范围内每日两次的空间分辨率为1 km的近红外可降水量数据，因为MODIS数据反演可降水量受云层的影响[13]，下载包含BJFS站的2014年和2015年的MODIS近红外可降水量数据和云掩膜产品，剔除BJFS站对应位置的有云影像，最终选择该站点的晴空影像。通过NASA网站(ftp://cddis.gsfc.nasa.gov/pub/gps/)获得与MODIS水汽值相同时间的2014年和2015年BJFS站的GPS观测数据和气象数据(温度、气压)，这两年该站的数据有部分缺失。

最后共得到2014年晴空条件下420对GPS_PWV和对应的MODIS_PWV数据用于建立回归模型，其中春夏秋冬四个季节各有107对、88对、115对和110对数据。选取2015年每个季节45对数据，共180对作为检验数据。

2 GPS可降水量反演原理及精度验证

2.1 GPS可降水量反演原理

GPS可降水量反演[1,11]主要分为三步：首先，根据NASA网站获得的BJFS站的大气压、纬度和大地高，使用Saastamoinen模型计算静力学延迟；其次，对流层延迟减去静力学延迟得到对流层湿延迟，对流层延迟从NASA网站下载得到；第三，对流层湿延迟乘以转换系数得到可降水量，本文采用纬度和年积日来计算转换系数。

2.2 精度验证

美国怀俄明大学提供每天0点和12点的可降水量实际观测数据，检验GPS反演可降水量的精度时，为代表全年的反演精度，选取2014年BJFS站每个月5日、10日、15日、20日、25日、30日0点和12点的GPS_PWV数据与实际观测的可降水量进行对比分析，因为该站2014年5月20日、25日，6月10日，8月5日，15日，10月15日，12月15日、30日GPS数据缺失，另外没有1月10日12点的实测PWV，最终得到125对GPS和对应的实际观测的可降水量，两者的比较图如图1所示，每对GPS_PWV和实测PWV的数值都很接近，两者趋势也保持一致见图1。由相关性分析可得两者之间呈现显著的线性关系，R2达0.973，RMS仅为2.29 mm。因此，GPS反演的可降水量准确性很高，可以作为标准值校正MODIS近红外可降水量数据。

3 GPS_PWV与MODIS_PWV的相关性分析

根据2014年420对GPS_PWV与MODIS_PWV数据，其中春夏秋冬四个季节各有107对、88对、115对和110对数据，做出两者之间四个季节和全年的比较图，如图2所示。通过相关性分析，发现GPS_PWV与MODIS_PWV之间呈现显著的线性相关性，相关系数和显著性sig值见表1。

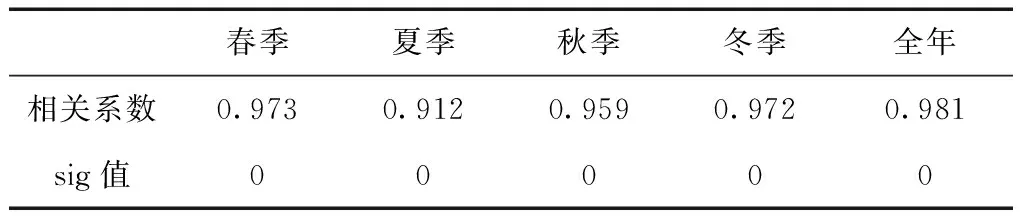
表1 四个季节和全年的GPS_PWV与MODIS_PWV相关系数和sig值

由图2可以看出，夏季GPS_PWV和MODIS_PWV较大，冬季GPS_PWV和MODIS_PWV较小，春季和秋季GPS_PWV和MODIS_PWV基本介于夏季和冬季之间。GPS_PWV和MODIS_PWV不同，存在一定的偏差，但是两者的变化趋势基本一致。由表1可得，四季和全年的GPS_PWV和MODIS_PWV间存在显著的线性相关性，相关系数均在0.9以上，其中全年的相关系数最大为0.981，春季和冬季的相关系数相当，分别为0.973和0.972，夏季的相关系数最小为0.912，说明两者的变化趋势基本一致；四季和全年的显著性sig值均为0，通过显著性检验。

图2 四个季节和全年的GPS_PWV与MODIS_PWV比较

4 GPS_PWV校正MODIS_PWV的模型建立与模型可靠性检验

4.1 模型的建立

由于GPS_PWV和MODIS_PWV之间有显著线性相关性，因此可以做线性回归分析。一元线性回归模型[14]为

y=a×x+b+ε.

其中，a，b是回归系数，ε为误差项。

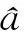
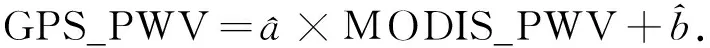
GPS_PWV全=0.794×MODIS_PWV全+0.256.

GPS_PWV春=0.766×MODIS_PWV春+0.304.

GPS_PWV夏=0.711×MODIS_PWV夏+4.458.

GPS_PWV秋=0.704×MODIS_PWV秋+1.632.

GPS_PWV冬=0.778×MODIS_PWV冬+0.015.

4.2 模型精度检验

把2015年每个季节45对检验数据，分别代入对应的季节线性回归方程和全年线性回归方程中，得到的结果与GPS_PWV做比较见图3。

从图3可以看出，GPS_PWV、季节模型校正的MODIS_PWV、全年模型校正的MODIS_PWV 3种曲线的变化趋势基本一致，季节模型校正的MODIS_PWV要比全年模型校正的MODIS_PWV更接近GPS_PWV，这说明季节校正模型的精度相对全年校正模型要高。为说明具体误差，GPS_PWV与MODIS_PWV、季节模型校正的MODIS_PWV、全年模型校正的MODIS_PWV之间的均值、绝对值均值、绝对值最大误差、均方根误差结果见表2和图4。

图3 GPS_PWV和MODIS_PWV的四季、全年模型校正值比较

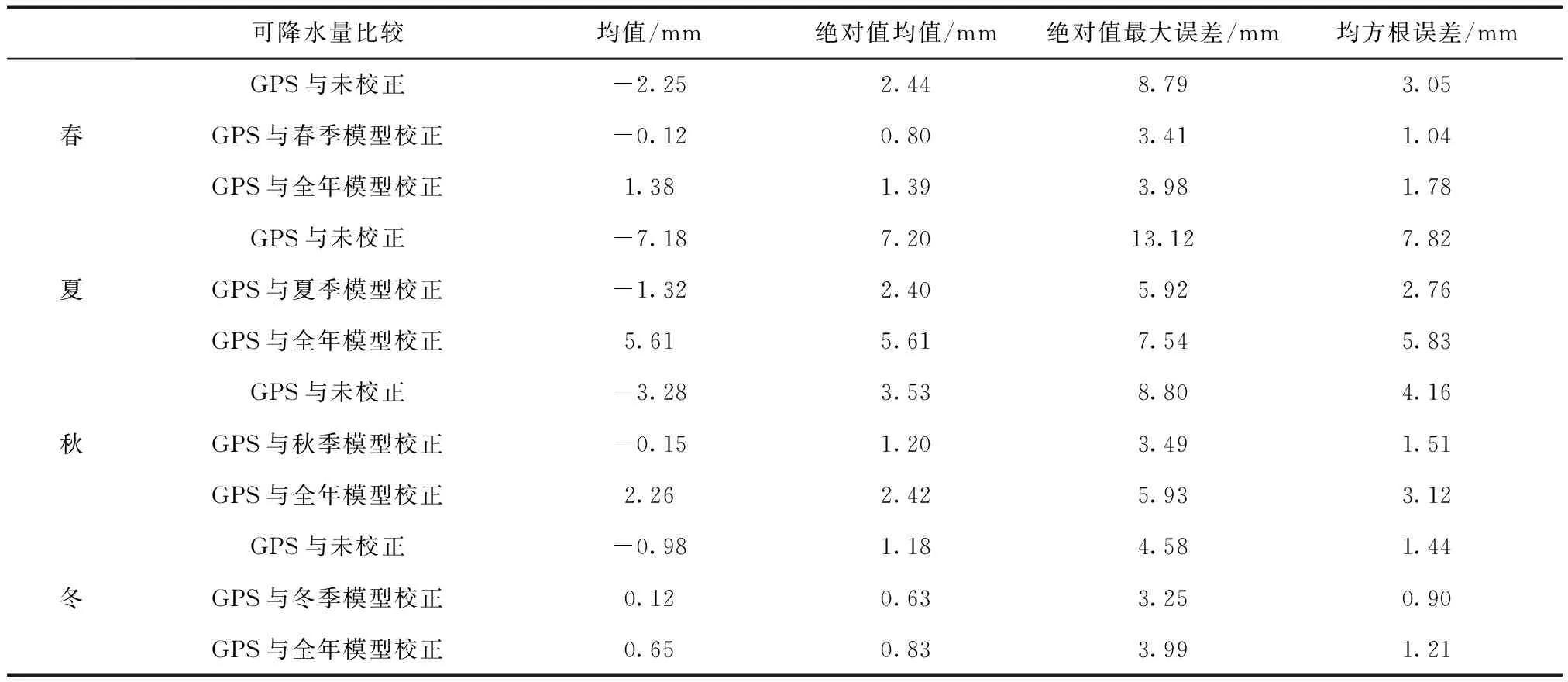
可降水量比较均值/mm绝对值均值/mm绝对值最大误差/mm均方根误差/mm春GPS与未校正-2.252.448.793.05GPS与春季模型校正-0.120.803.411.04GPS与全年模型校正1.381.393.981.78夏GPS与未校正-7.187.2013.127.82GPS与夏季模型校正-1.322.405.922.76GPS与全年模型校正5.615.617.545.83秋GPS与未校正-3.283.538.804.16GPS与秋季模型校正-0.151.203.491.51GPS与全年模型校正2.262.425.933.12冬GPS与未校正-0.981.184.581.44GPS与冬季模型校正0.120.633.250.90GPS与全年模型校正0.650.833.991.21

由表2和图4可知，经过模型校正后的MODIS_PWV精度更高，均值、绝对值均值、绝对值最大误差和均方根误差都要小于校正之前。季节模型校正的MODIS_PWV要比全年模型校正的MODIS_PWV精度高，季节模型校正后的4个误差统计值均小于全年模型。

在四个季节校正模型中，夏季校正模型的精度最低，但要高于全年模型，未校正之前的均方根误差为7.82 mm，全年模型校正后的均方根误差为5.83 mm，季节模型校正后的均方根误差为2.76 mm，未校正之前的均方根误差约是季节模型校正后的2.8倍，全年模型校正后的均方根误差是季节模型校正后的2倍多；冬季校正模型的精度最高，未校正之前的均方根误差为1.44 mm，全年模型校正后的均方根误差为1.21 mm，季节模型校正后的均方根误差为0.90 mm，未校正之前的均方根误差约是季节模型校正后的1.6倍。

总体上看，校正之后的MODIS_PWV要比校正前精度高，季节模型的校正效果要比全年模型好。四个季节的线性回归方程可以用于校正MODIS_PWV。

5 结 论

通过利用BJFS站的GPS_PWV和MODIS_PWV进行相关性分析，首次建立季节和全年的校正模型并验证结果，主要得出以下结论：

1)GPS_PWV和MODIS_PWV的变化趋势基本一致，存在系统性偏差，四季和全年GPS_PWV和MODIS_PWV的相关系数分别为0.973、0.912、0.959、0.972和0.981，sig值都为0，存在显著相关性。

2)以GPS_PWV为标准值，建立四个季节和全年的线性回归模型，校正后的MODIS_PWV比校正前精度高，四个季节模型校正后的MODIS_PWV与GPS_PWV的均方根误差都小于3 mm，四个季节校正模型的精度都要高于全年校正模型。

本文提出的季节性模型可以获得更加精确的区域性连续的可降水量信息，为气象学短期预报和InSAR大气校正提供参考。

[1] 王勇,刘严萍.地基GPS气象学原理与应用研究[M].北京:测绘出版社,2012.

[2] CHOY S, WANG C S, YEH T K, et al.Precipitable Water Vapor Estimates in the Australian Region from Ground-Based GPS Observations[J].Advances in Meteorology, 2015, 2015:1-14.

[3] 常亮,郭立新,冯贵平.MODIS红外水汽校正及其在InSAR大气改正中的应用[J].大地测量与地球动力学,2016,36(1):47-51.

[4] KULKARNI K, KUNTE K J, SONAWANE S H, et al.Calibration and Evaluation of Precipitable Water Vapor From MODIS Infrared Observations at Night[J].IEEE Transactions on Geoscience & Remote Sensing, 2015, 53(5):2612-2620.

[5] 范士杰, 臧建飞, 刘焱雄,等.GPT/2模型用于GPS大气可降水汽反演的精度分析[J].测绘工程, 2016, 25(3):1-5.

[6] 李红林, 李万彪.MODIS近红外资料反演大气水汽总含量[J].北京大学学报(自然科学版), 2008, 44(1):121-128.

[7] SOHN D H, CHO J, SOHN D H, et al.Trend Analysis of GPS Precipitable Water Vapor Above South Korea Over the Last 10 Years[J].Journal of Astronomy & Space Sciences, 2010, 27(3):231-238.

[8] 李艳永,崔彩霞,赵玲,等.基于MODIS的近红外大气水汽含量的反演及其与地基GPS水汽的对比分析[J].沙漠与绿洲气象,2010,6(4):30-33.

[9] 方圣辉,毕创,乐源,等.利用GPS可降水量校正MODIS近红外水汽数据[J].测绘科学,2016,41(9):38-41.

[10] 侯建国,杨成生,张勤,等.GPS可降水汽与MODIS可降水汽回归性分析[J].地理与地理信息科学,2010,26(2):42-45,113.

[11] 曹艳丰,陈宝献,陈秀万,等.基于GPS数据的MODIS大气可降水量反演精度提高模型[J].遥感信息,2014,29(2):21-25.

[12] 张俊东,陈秀万,李颖,等.基于GPS数据的MODIS近红外水汽改进反演算法研究[J].地理与地理信息科学,2013,36(2):40-44.

[13] 张天龙,韦晶,甘敬民,等.利用MODIS近红外数据反演大气水汽含量研究[J].光谱学与光谱分析,2016,36(8):2378-2383.

[14] 汪冬华.多元统计分析与SPSS应用[M].上海:华东理工大学出版社,2010：94-95.

[责任编辑：李铭娜]

SeasonalmodelestablishmentofMODISnearinfraredprecipitablewatervaporbasedonGPS

DUAN Xixi1，QU Jianguang2, GAO Wei1，WANG Shuaimin1

(1.School of Geology and Geomatics, Tianjin Chengjian University, Tianjin 300384, China; 2. College of Surveying and Mapping Engineering, Heilongjiang Institute of Technology, Haerbin 150050, China)

Considering the change of precipitable water vapor with the season, this paper puts forward to establish a seasonal model of MODIS near infrared precipitable water vapor based on GPS. Firstly, it carries out the correlation analysis of MODIS near infrared moisture product and precipitable water vapor by the meteorological data and zenith tropospheric delay data of Beijing Fangshan (BJFS) station. Results show that MODIS near infrared moisture product changes consistently with precipitable water vapor retrieved from ground-based GPS technology. There is a significant positive correlation of them. Then, GPS PWV is taken as the standard precipitable water vapor. The seasonal and annual calibration models are established by using the regression analysis. The RMS value of water vapor calculated from ground-based GPS technology and calibrated MODIS near infrared moisture product is less than 3mm, and the maximum error is not more than 6mm. The precision of seasonal calibration models is higher than annual calibration model.

GPS; precipitable water vapor; MODIS; calibration; seasonal model

P228

A

1006-7949(2017)12-0021-06

2017-01-25

段茜茜(1991-)，女，硕士研究生.