角反射器差分干涉方法及反距离加权最小费用流相位展开算法
2017-12-13王国锋李建成宋鹏飞傅文学
王国锋,李建成,宋鹏飞,傅文学
(1.中国公路工程咨询集团有限公司,北京 100089; 2.中国科学院 遥感与数字地球研究所,北京 100094)
引用著录:王国锋,李建成,宋鹏飞,等.角反射器差分干涉方法及反距离加权最小费用流相位展开算法[J].测绘工程,2017,26(12):27-31,37.
DOI:10.19349/j.cnki.issn1006-7949.2017.12.005
角反射器差分干涉方法及反距离加权最小费用流相位展开算法
王国锋1,李建成1,宋鹏飞1,傅文学2
(1.中国公路工程咨询集团有限公司,北京 100089; 2.中国科学院 遥感与数字地球研究所,北京 100094)
合成孔径雷达差分干涉测量(Differential Interferometric Synthetic Aperture Radar, DInSAR)在低相关区由于受时间空间去相关的影响,无法得到有效应用。角反射器DInSAR方法能在长时间段内保持幅度和相位稳定性,可以最大程度地减小去相关的影响。但由于反射器在空间上一般形成不规则稀疏网络分布,在平地相位、高程相位计算及相位展开方法上都带来新的挑战。研究三角反射器的DInSAR技术,重点分析基于不规则离散点的最小费用流相位展开算法。对费用流算法权重的选择,通过分析残差的产生来源,提出以弧所穿越的边长度倒数作为弧费用的权重设置方法,解决费用流算法中具有相同费用路径的选择问题。最后将角反射器DInSAR技术应用于滑坡移动的监测,通过对140 d时间段的监测,得到与实测值具有较好一致性的结果。
三角反射器; 合成孔径雷达差分干涉; 最小费用流; 反距离加权; 相位展开; 去相关
合成孔径雷达差分干涉测量技术(DInSAR)利用相邻轨道雷达数据的差分干涉相位与地表形变信息相关的特性[1-2],从而对地表微小形变进行高精度监测,具有高分辨率、大面积、全天时全天候和实时性,在空间对地观测领域是一项极具潜力的技术,得到了广泛的应用[3-5]。然而DInSAR应用中的一个最大局限性是去相关的影响。在差分干涉雷达数据获取的不同时间点上,自然地物的物理性质发生变化,引起干涉像对之间的相关性降低,从而不能生成理想的干涉条纹,导致干涉图的相位无法准确展开,得不到正确的绝对相位值,因此DInSAR技术无法实施。
近年来出现了一系列的技术试图减小去相关的影响,如永久散射体(Permanent Scatterer, PS)技术[5-7]、角反射器DInSAR技术[8-9]等等,基本思想都是利用具有长时间稳定特性的散射点,计算差分干涉相位,分析相位变化特征,从而建立与地表形变之间的关系。但在地形复杂的滑坡区,由于地质地貌及地表覆被的性质,一般都具有严重的低相关特征,从而提取不出足够数量的自然稳定点。采用角反射器的DInSAR技术对滑坡移动进行监测是一个行之有效的方法,但一些关键技术问题目前仍处于研究之中,如平地相位、高程相位的精确计算和相位展开算法等。本文结合对滑坡体移动的监测研究,分析角反射器的DInSAR技术的平地相位和高程相位去除方法,并重点研究了相位展开方法,提出基于离散点的反距离加权最小费用流相位展开算法。实际的应用表明,角反射器DInSAR技术可以得到理想的结果。
1 角反射器DInSAR技术
角反射器是由相互垂直的三块三角平面板拼接而成的一个空心锥体,利用导电性能和电磁性能良好、电容率大的金属材料(一般选铝)制成,表面为实体或网状的一种点状人工地物目标,在地物目标分类中属于硬目标。三角反射器是一个回射器,即微波进入反射器会被反射回入射来的方向。由于对微波的吸收极小而反射强度很大,当聚焦良好时,会在雷达图像上表现为一个十分醒目的亮点。
三角反射器的特殊结构使得它的微波反射强度十分稳定,相位信号亦是稳定的,即使经过几年的时间,仍然能保持很高的相关性。因此,在研究时段内,所获取的时间基线相隔较长、空间基线接近甚至达到临界基线长度的所有影像对可以被充分利用。
要使三角反射器在雷达图像上达到其最大的反射强度,它的几何对称轴方向必须与雷达视线方向重合。对正侧视雷达,只须将角反射器的对称轴调整到卫星轨道的垂线上。由于角反射器的对称轴只是一个几何存在,因此要准确地调整好它的指向,必须采用间接的方法,可以利用角反射器的几何结构方便地加以确定,Ge等对反射器的具体安装方法做了详细地研究[9]。
1.1 三角反射器峰值相位提取
三角反射器在雷达图像上的回波信号很强,所在像素信号几乎只反映它的存在,可以提供精确的定位及幅度信息。然而其脉冲响应主瓣的最大值在雷达有限采样频率下,不一定总被采集到,因此需要用插值方法提取峰值相位信息,具有相位保存能力的插值设计即成为要解决的问题。一般来说,雷达系统的设计都满足Nyquist采样定理,因此频域的采样率变换是一个理想的插值方法,从理论上逼近于二维sinc插值函数。为尽量减小峰值提取误差,插值精度要能达到0.01像元。
1.2 差分干涉相位计算
干涉像对三角反射器峰值相位的差值不仅包含有反映地表形变的相位信息,还有平地相位、反射器的高程相位以及系统误差和大气相位信息,因此需要从干涉相位中去除平地相位和高程相位。人工布设的三角反射器地理坐标位置可以得到精确的测量,结合相应的卫星轨道信息即可精确地去除平地相位和高程相位。
1.2.1 平地相位
平地相位表示为
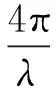
(1)
其中,λ为载波波长;S1P和S2P分别为主图像和辅图像卫星S1,S2与反射器在参考面投影点之间的距离。
1.2.2 高程相位
关于高程相位提出了一些数学模型,需考虑数据类型及其参数。当反射器的高程和地理坐标已知,结合卫星轨道数据的高程相位计算方法可参考舒宁等[10]。
2 反距离加权的最小费用流相位展开
最小费用流(Minimum Cost Flow, MCF)相位展开算法由Costantini提出[11],从算法思想上仍然属于全局优化,对路径跟踪法和最小二乘法不能很好兼顾运算速度和精确性的问题给出了较为理想的解决方案。该算法既有很强的抗噪声能力,又能够很好地保持与真实相位的一致性,因此得到了重视和发展。一般来说,三角反射器在空间上是不规则的稀疏网格,基于规则网格的常规相位展开算法无法直接进行求解。有效解决办法是首先构建Delaunay三角网,考虑三角网内每个三角形单元的残差,再经过网络流算法确定合理的枝切线,最后在枝切线的指导下通过沿路径积分法恢复每个反射器的真实相位。
2.1 三角网残差点的确定
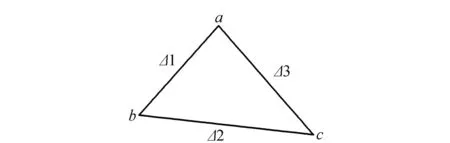
在Delaunay三角网中,定义三角形的相位场是连续的或无旋的:①相位值定义;②三角形相邻顶点的真实相位差在(-π, π]之间。但由于地表形变量过大及其它相位等因素的影响,真实的相位场一般是有旋的。在三角网中引入残差点的概念,如图1所示,在三角形abc中:
Δ1=W[ψb-ψa],
Δ2=W[ψc-ψb],
Δ3=W[ψa-ψc].
其中,缠绕函数W[x]定义:
W[x]=x+2kπ,-π (2) 残差的判断准则: (3) 图1 三角形的残差 2.2 最小费用流相位展开 在Delaunay三角网中若存在残差点,相位展开前必须确定路径枝切线。所谓枝切线是这样的一些线,它连接所有的正负残差点,并在相位展开时避免积分路径穿越这些线。对一幅具有残差点的干涉图来说,有多种枝切线的连接方法,不当的枝切线设置会造成误差传递。因此寻找合理的枝切线设置算法是相位展开精确程度的决定性步骤[12-13]。 在不规则稀疏网络相位展开中,最小费用流算法具有其合理性和有效性。最小费用流算法是基于容量-费用网络,定义如下[14]: 定义:在以V为节点集,A为弧集的有向图G=(V,A)上定义权函数: 1)C弧上的权函数,弧(i,j)∈A对应的权C(i,j)记为cij,称为弧(i,j)的单位流量的费用; 2)L弧上的权函数,弧(i,j)∈A对应的权L(i,j)记为lij,称为弧(i,j)的容量下界; 3)U弧上的权函数,弧(i,j)∈A对应的权U(i,j)记为uij,称为弧(i,j)的容量; 4)D顶点上的权函数,节点i∈V对应的权D(i)记为di,称为顶点i的供需量。 此时所构成的网络称为容量-费用网络,可以记为N=(V,A,C,L,U,D)。一般来说,总是可以把L≠0的网络转化为L=0的网络进行研究,因此,可以假设总满足L=0。 最小费用流就是在这样的网络中寻找总费用最小的可行流,该问题可描述: (4) s.t. 0≤xij≤uij,∀(i,j)∈A. 在稀疏点构成的Delaunay三角网中,对应于顶点上的供需量为三角形的残差,第一个约束条件为 (5) 如图2所示,实线网络对应的是三角反射器构成的Delaunay三角网,虚线网络为相应的对偶图。以每个三角形的残差值为对偶图顶点的容量,即构成了容量-费用网络。对上述的最小费用流问题进行求解,即可得出以三角网残差值为对应顶点的网络所有弧上的流值。由于流值的容量设为1,则流值为0的弧,相位积分可直接进行;而在流值为±1的弧,相位积分的路径应避免穿过该弧,或在穿过该弧时将相位加上或减去2π再进行积分。这样从基点出发,确定出积分路径,所有点的绝对相位即可获得。 图2 Delaunay三角网和对偶图 最小费用流的相位展开思想即把残差引起的误差控制到最小,但当有残差存在的时候,得到的枝切线并不一定总能真实地反应相位跳跃的位置,因而也无法还原出其真实相位,相位展开结果的误差即来源于此。 2.3 最小费用流算法弧费用权重的选择 最小费用流相位展开的优点是将相位展开问题归结为数学问题上,物理意义非常直观,同时算法实现的效率很高。目前,基于网络规划的相位展开算法研究,都是提取出相干系数较高的像元点处的差分干涉相位集合对象[15]。当稀疏点为相干性高的点时,如果研究区较小,且成像质量很好,则网络流的权重基本都可以选择为1,即式(4)中cij=1。但这样会带来一定的问题,即费用流相同路径的选择问题。考察图2,其中点1为正残差点,点3为负残差点,则将这两个正负残差点连接的路线可选择1-2-3或1-4-3 ,当费用权重为1时,这两条路径将得到相同的费用。 更一般地,当枝切线路径上的两个点位于一个具有偶数条边多边形的对角顶点的时候,都会出现两条费用流相同的可供选择的路径。因此,弧权重的确定是网络规划相位展开算法的一个值得研究之处。 在相位残差形成的原因上,可以认为相邻两点差分干涉相位跳跃出现的概率随该两点间距离的增加而增大。因此,可以将枝切线穿越的相邻三角反射器连线的长度纳入到权重构建里,以反映两点之间的距离在差分干涉相位跳跃产生中所起的作用。对图2的两条枝切路径进行分析,1-2-3的枝切穿越的两条弧a-e和e-b的长度和小于1-4-3枝切线所穿越的两条弧d-e和e-c的长度之和,从出现相位残差的概率出发,认为枝切线1-4-3的枝切路径设置更为合理。 基于上面的分析,在利用最小费用流对不规则稀疏网络进行相位展开时,将每条弧所穿过的边长倒数赋为该段弧的费用权重值,其物理意义即为两稀疏点之间的距离越大,则在干涉图中产生相位跳跃的可能性越大。于是在式(4)中: (6) 其中,rij为i,j两顶点连线所穿越的弧的长度。 研究选择三峡地区的滑坡,在滑坡上布设了一系列的三角反射器,并获取了5景研究区的ENVISAT ASAR数据。充分利用数据,尽量避免使用时间基线过长的像对,本次研究中采用了多主图像像对选择方法,共生成6个干涉像对。最大时间基线为70 d,最大空间基线垂直分量为729.34 m。采用距离-多普勒定位算法确定出每幅图像中的三角反射器的位置,利用频域采样率变换算法对图像进行100倍插值,从中提取出反射器的峰值相位,这样各像对的反射器也就自动获得了配准,峰值相位之差即为干涉相位。 结合反射器的空间地理位置和卫星轨道数据,去除平地相位和高程相位,获得差分干涉相位。采用逐点插入法将滑坡体上的三角反射器进行Delaunay三角网剖分,共得到16个三角形,对每个三角形进行编号,如图3所示中黑线网络所示。取每个三角形的中心点,联成对偶图,如图中红线网络。对偶图的每条边只与Delaunay三角网的一条弧相交。在最小费用流相位展开算法中,正是各条边对应的流值确定了枝切线。 图3 Delaunay三角网的构建和枝切线的确定 根据Delaunay三角网中每个三角形的关联顶点三角反射器相位值,选逆时针方向为正方向计算残差,并将残差值赋予相应的对偶图网络顶点,作为费用-容量网络各节点的供需量,6个干涉像对的16个三角形的残差值如表1所示。可以看出,时间基线为70 d的干涉像对,其差分干涉相位都存在着相位残差;而时间基线为35 d的像对,其差分干涉相位都不存在有残差。分析其原因,该滑坡体在三峡水库蓄水后,滑坡底部受江水的浸泡作用,移动速度加快。而时间基线为70 d的像对,由于时间间隔较大,滑坡体的移动导致了三角反射器之间发生了相位跳跃,即相邻的反射器相位变化超出了一个2π的整周期,因此在三角网中出现了相位残差。而时间基线为35 d的像对,时间基线较短,滑坡的移动并未引起相位跳跃。在利用角反射器的DInSAR技术时,应尽可能的使干涉像对的时间基线最小,采用多主图像的干涉像对序列是合适的。这样的残差分布也表明本次的差分干涉相位的计算是可信的。 表1 各干涉像对Delaunay三角网的残差分布 考察图3对偶图网络顶点8为正残差点,顶点10为负残差点,根据最小费用流算法,当弧费用权重为1 时,则这两个正负残差点连接路径可选择8-11-10 或8-7-10,将得到相同的费用。当考虑距离加权时,由于8-11-10的枝切穿越的两条弧长度和小于8-7-10枝切线的两条弧长度之和,因此枝切线8-7-10 的枝切路径设置更为合理。 这样,从基点ZRS12出发,避开枝切线,沿路径对差分干涉相位进行积分,即得到所有三角反射器的展开相位。对展开相位建立相位系统方程,利用最小二乘法对系统方程进行求解即可得到三角反射器的移动量。 由于反射器12布设在稳定的基岩上,认为其移动量为0,监测的结果为非0值则认为是大气效应、系统误差等因素引起的。在研究区不大时,可以参考点对其余各点误差进行结果修正。本次研究的140 d的实测结果与三角反射器的DInSAR监测结果对比如图4所示,实测值与监测结果进行线性回归分析,黑色虚线为实测值与监测值等值线,红色线为线性回归直线,显示出了较好的线性相关性。 图4 实测值与三角反射器的DInSAR 监测的结果比较 角反射器具有幅度和相位的稳定性,能在长时间段内保持高相关,最大限度地减小时间空间去相关的影响。三角反射器的DInSAR技术可以有效地用于低相关区的地表变化监测中,空间基线较大甚至达到临界基线的像对仍然可以进行干涉处理,充分地利用了数据资源。但在干涉像对的选取时,应尽量使用时间基线较短的像对,以免引起相邻反射器的相位跳跃。 人工布设的三角反射器一般在空间上形成不规则网络,最小费用流相位展开算法可以为不规则网络确定出合理的枝切路径设置方法。本文提出了采用弧穿越的反射器连线长度的倒数作为弧费用的权重,解决了具有相同费用的不同路径选择问题。从物理意义上,该权重的设置反映了相邻反射器之间距离越大越容易引起相位跳跃的事实。角反射器的DInSAR应用实例表明,该技术的监测结果与实测结果得具有很好的一致性,完全能使用于较小区域的地表变化监测中。 [1] GRAHAM L C. Synthetic interferometric radar for topographic mapping [C]. Proceeding IEEE, 1974, 62: 763-768. [2] ZEBKER H A, GOLDSTEIN R M. Topographic mapping from interferometric synthetic aperture radar observations [J]. Journal of Geophysical Research, 1986, 91(B5): 4993-4999. [3] LANARI R, SANSOSTI E. ERS Differential SAR Interferometry: A powerful tool for surface deformation analysis [C]. Radar Conference, 2008. RADAR '08. IEEE, 1-6. [4] ROMEISER R. Current Measurements by airborne along-track InSAR: measuring technique and experimental results [J]. IEEE Journal of Oceanic Engineering, 2005, 30(3): 552-569. [5] 马德英, 刘国祥, 蔡国林, 等. 短时空基线PS-DInSAR提取地表形变时间序列 [J]. 西南交通大学学报, 2009, 44(1): 77-82. [6] FERRETTI A, PRATI C, ROCCA F. Permanent scatterers in SAR interferometry [J]. IEEE Transactions on Geoscience and Remote Sensing, 2001, 39(1): 8-20. [7] 罗小军, 刘国祥, 黄丁发, 等.永久散射体网络建模及地表形变与大气影响分析 [J]. 遥感学报, 2008, 12(2): 271-276. [8] XIA Y, KAUFMANN H, GUO X F. Differential SAR interferometry using corner reflectors [C]. Geoscience and Remote Sensing Symposium, 2002, 2: 1243-1246. [9] GE L, RIZOS C, HAN S, et al. Mining subsidence monitoring using the combined InSAR and GPS approach [C]. The 10th FIG international symposium on deformation measurements. California: Orange. 2001. [10] 舒宁.雷达影像干涉测量原理 [M]. 武汉: 武汉大学出版社, 2003. [11] COSTANTINI M. A novel phase unwrapping method based on network programming [J]. IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 813-831. [12] FLYNN T J. Consistent 2-D phase unwrapping guided by a quality map [C]. Proceedings of the 1996 International Geoscience and Remote Sensing Symposium. Lincoln. Nebraska. IEEE. PISCATAWAY, 1996, 2057-2059. [13] BUCKLAND J R, HUNTLY J M, TURNER S. Unwrapping noisy phase maps by use of a minimum-cost-matching algorithm [J]. Applied Optics, 1995, 34(23): 5100-5108. [14] 谢金星, 邢文训, 王振波.网络优化[M].2版.北京: 清华大学出版社. 2009. [15] YU Y, WANG C, ZHANG H, et al. A phase unwrapping method based on minimum cost flows method in irregular network [C]. Proceeding IGARSS' 02, 2002, 3:1726-1728. [责任编辑:李铭娜] CornerreflectorsDInSARandinversedistanceweightedMCFphaseunwrappingmethod WANG Guofeng1, LI Jiancheng1, SONG Pengfei1, FU Wenxue2 (1. China Highway Engineering Consulting Corporation, Beijing 100089,China; 2. Institute of Remote Sensing and Digital Earth, Chinese Academy of Sciences, Beijing 100094,China) Difference interferometric synthetic aperture radar (DInSAR) has been a very powerful technique for the measurement of land deformations, but the coherence degradation will seriously affect the quality of interferogram in the low coherence area. Corner reflector DInSAR can compensate for the limitation of the classical DInSAR due to the stable amplitude and phase performance of the reflector. However, the corner reflectors are irregular discrete points in spatial, so it is necessary to develop the new methods for calculating the flat earth phase and the elevation phase and the phase unwrapping. In this paper, the corner reflectors DInSAR technique is analyzed and the minimum cost flow (MCF) phase unwrapping method based on the irregular sparse grid is discussed. Through analyzing the resources of the phase residues, the inverse distance weighted MCF phase unwrapping method is proposed which can decide which branch-cut is the more appropriate when there are two same cost flow paths. Finally, the corner reflectors DInSAR is used for monitoring the movement of Shuping landslide, and the monitoring result is in good agreement with the measurement in site, which shows that corner reflectors DInSAR allows monitoring the ground deformation in low coherence area and provides accurate results. corner reflector;DInSAR;minimum cost flow;inverse distance weighted;phase unwrapping;decorrelation P231 A 1006-7949(2017)12-0027-05 2016-10-13 中国交建科技项目(2013-ZJKJ-23);交通运输部信息化技术研究项目(2014-364-J03-090) 王国锋(1958-),男,博士.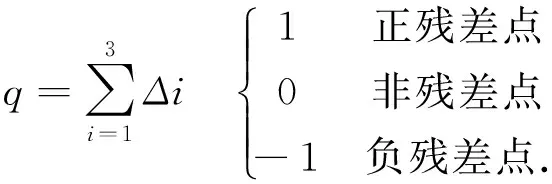
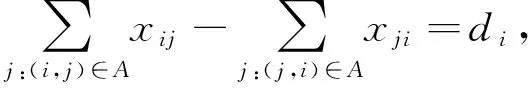
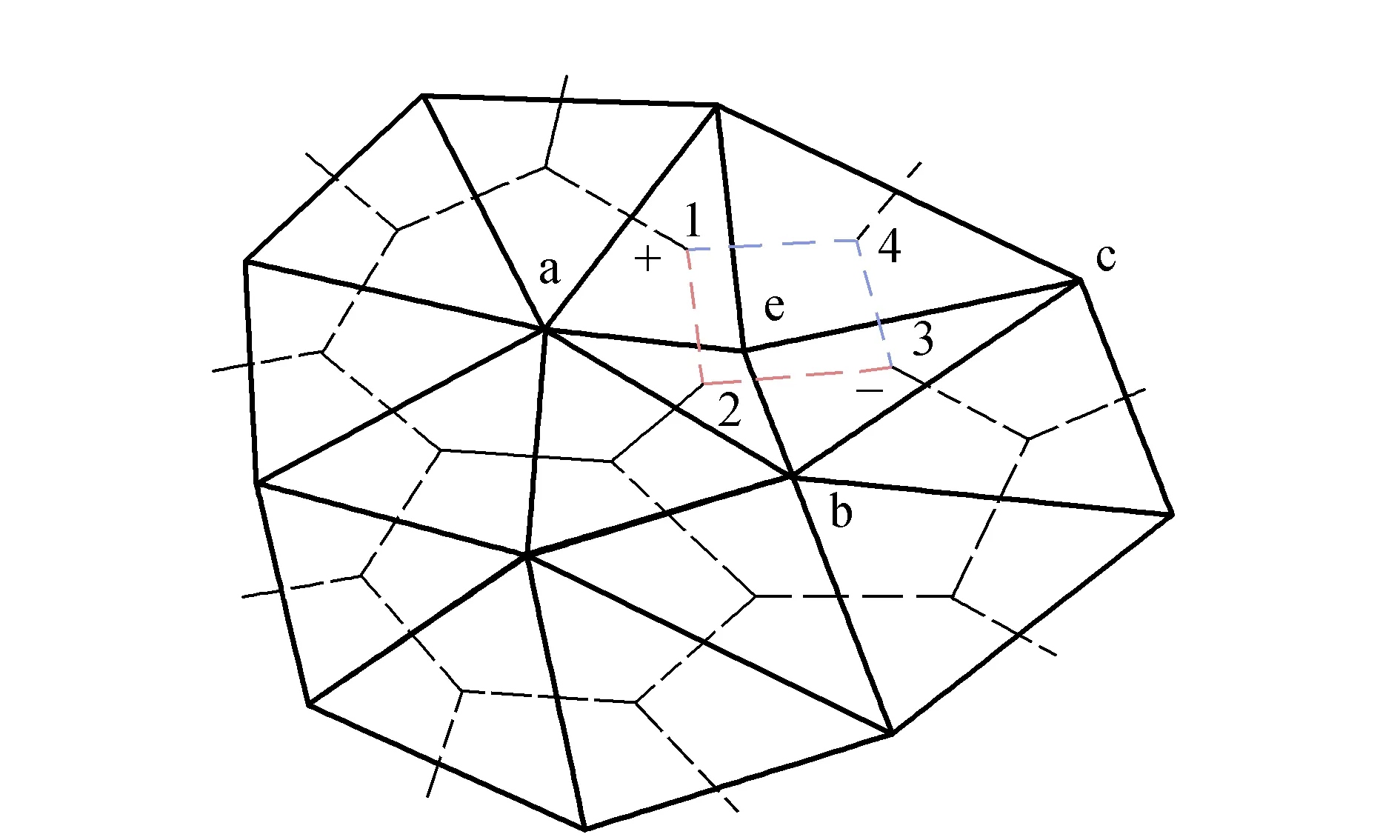

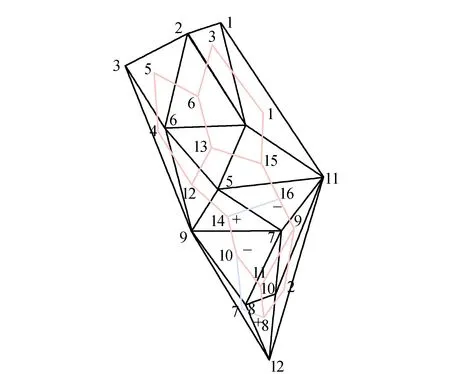
3 实验与结果
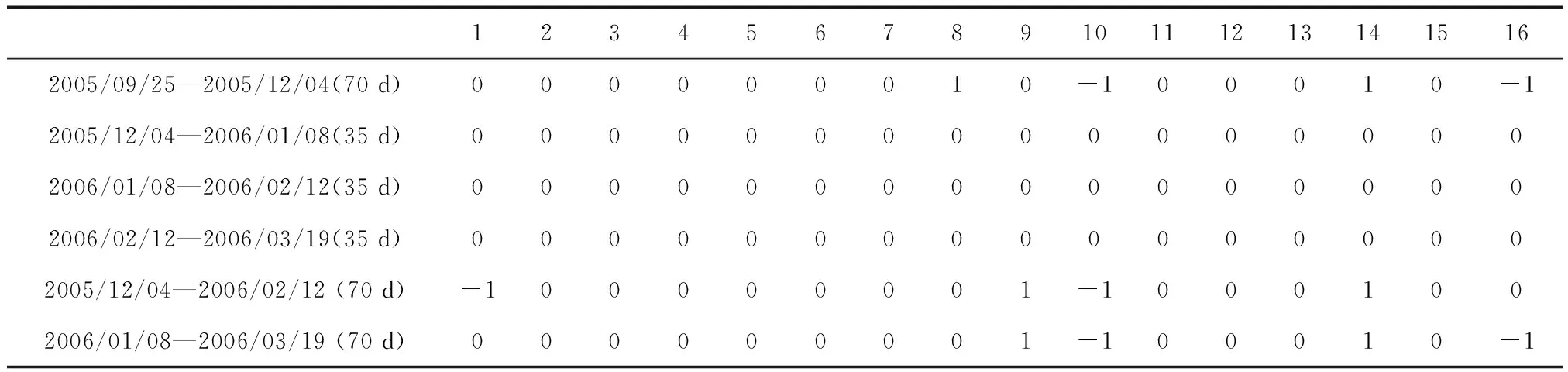
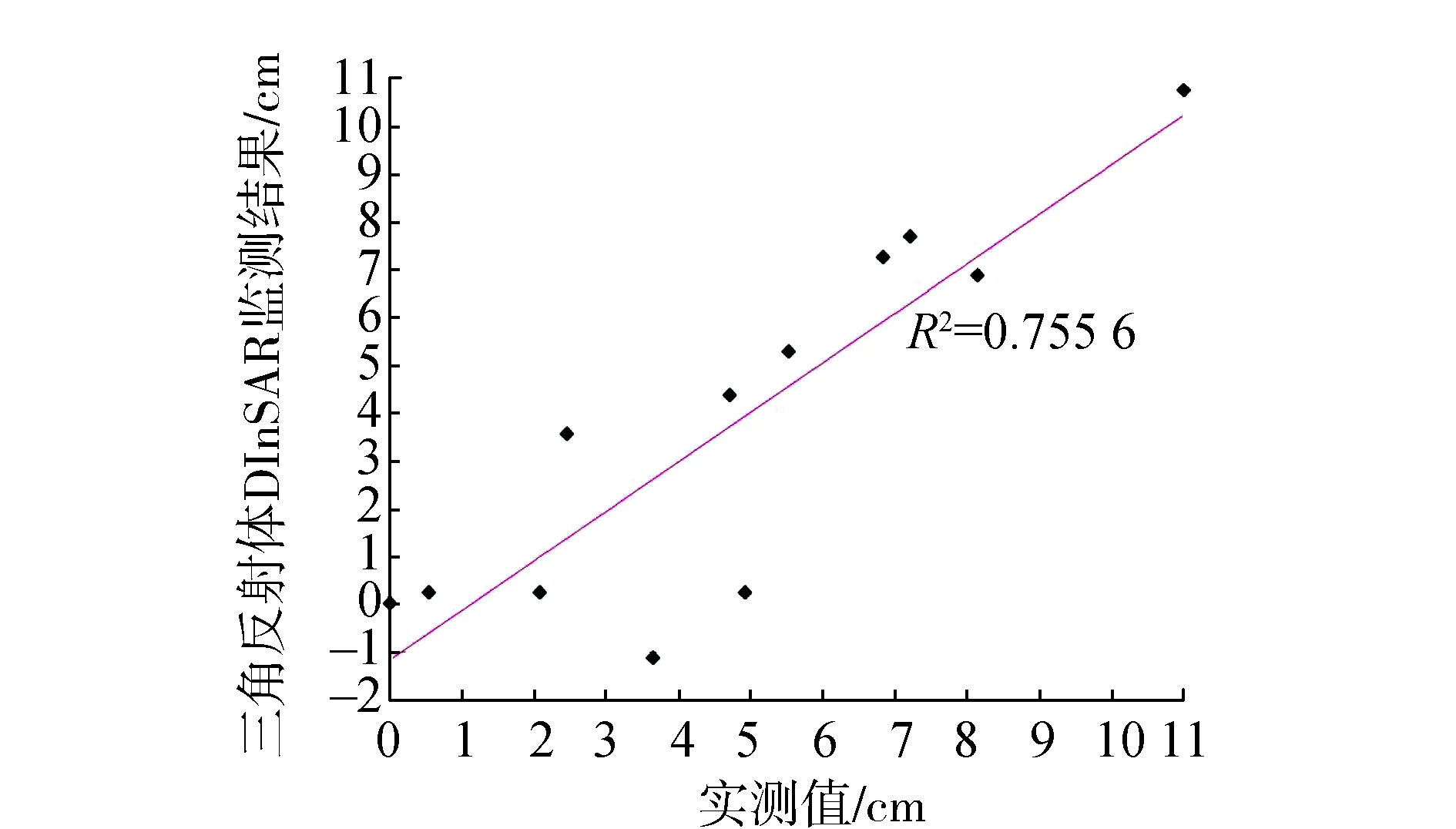
4 结束语
