“ 先分后合法”在匀强电场中的运用

云南 蒋金团

化繁为简，提升效率。

“ 先分后合法”在匀强电场中的运用

带电粒子在匀强电场中做无约束曲线运动时，通常的解答思路是：先构造等势面，后画电场线，利用两线相垂将粒子能的信息和力的信息联系在一起，从而找到突破口。笔者觉得这种思路比较繁琐，效果不是很理想，但换一种思路，正交分解电场的话，往往化繁为简，方便快捷。接下来，将选择两道模拟题展示正交分解的巧妙之处，感兴趣的朋友可上网查阅参考答案，将参考答案和笔者的解法进行对比。

( )

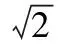
图1

A．50 V/m，方向B指向A

B．50 V/m，方向A指向B

C．100 V/m,方向B指向A

D．100 V/m,方向A指向B

【解析】该电场是一个匀强电场，可采用正交分解求解，正交分解的坐标系可以任意建立，考虑到x轴上有电势差，可将匀强电场分解成沿着x轴的分量和垂直x轴的分量，即y轴分量，根据匀强电场的电势差公式，有：

B.在x1与x3处受到磁场B的作用力大小之比为3∶1

C.从x1到x2与从x2到x3的过程中通过R的电量之比为5∶3

D.从x1到x2与从x2到x3的过程中R产生的焦耳热之比为3∶5

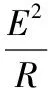
图7

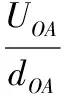
【答案】C

【思考】(1)本题中的A、B两点都在坐标轴上，若有一点不在坐标轴上，该如何找出该点到坐标原点之间的电势差与两个分场强以及该点坐标三者间的关系？

(2)如果题目给出试探电荷的电量且已知试探电荷沿两条路径移动时电场力做的功，该如何求出两点间的电势差？如何判断电势的高低？求出电势差后，如何求合场强？

【例2】如图所示，在直角坐标系第一象限内有A(6 cm，2 cm)、B(12 cm，8 cm)两点，匀强磁场垂直于xOy平面向外。一带负电的粒子q=1.6×10-19C，质量为m=3.9×10-23kg，以v0=16 m/s的速度从坐标原点O沿x轴正方向入射。不计重力。

图2

(1)为使带电粒子经过B点，求磁感应强度的大小。

(2)在第一象限内再加入平行xOy平面的匀强电场，并改变磁感应强度的大小，带电粒子可先后经过A、B两点，动能分别变为初动能的2倍和5倍，求电场强度。

【解析】第一问考查的是磁场中的圆周运动，第二问考查的是电磁叠加场的曲线运动，因为洛伦兹力不做功，且电场力做功是与路径无关，所以仍然采用正交分解的策略处理电场力做功问题。

(1)如图3所示，由几何关系R2=122+(R-8)2

得R=13 cm

得B=0.03 T

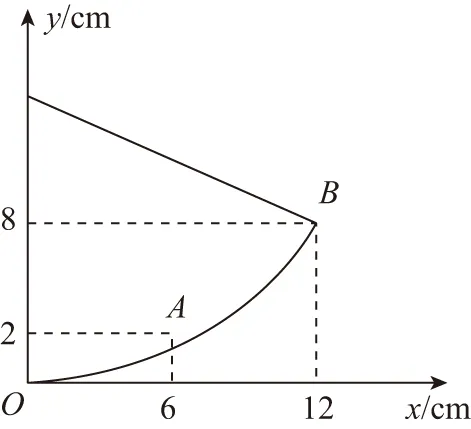
图3

(2)为方便求解电场力做功，设匀强电场的水平分量为Ex，竖直分量为Ey,

粒子从O点到A点由动能定理

qExxA+qEyyA=2Ek0-Ek0，

代入数据化简得6Ex+2Ey=3.12 V/m

粒子从O点到B点由动能定理

qExxB+qEyyB=5Ek0-Ek0

代入数据化简得6Ex+4Ey=6.24 V/m

联立解得Ex=0,Ey=1.56 V/m

所以E=Ey=1.56 V/m

【点悟】(1)本题中用W=qEl计算电场力做功时，q和l都取了绝对值，因此E值的正负代表功的正负，不代表场强的方向，那么场强的方向该怎么判断？

(2)第二问中，洛伦兹力不做功，为我们书写动能定理提供了方便，为了增加计算的难度，我们可以加入重力做功？重力做功和电场力做功有何相似的地方？

(作者单位：云南省施甸县第一中学)

四川省成都市石室中学)