数学思想在生物教学中的渗透
2017-12-13甘肃尚艳霞
甘肃 尚艳霞
数学思想在生物教学中的渗透
甘肃 尚艳霞
通观近几年高考,对学生的识图能力考查的力度逐年加大。因此,在高中生物学教学过程中,如果教师能够运用数学思想解答一些生物学问题,不仅可以适应新一轮课改的要求,还能实现高考“能用文字、图表以及数学方式等多种表达形式准确地描述生物学方面的内容”的能力目标。同时也可将一些复杂的生物学问题简单化,抽象的问题直观化,可以帮助学生对生物学知识的理解和掌握更灵活、更全面,提高学习效率。现将笔者在课堂中经常渗透的三种数学思想归纳如下:
1.集合思想
在小学数学中,学生就已经尝试利用集合图来解题,这在生物教学中也同样适用。首先,运用集合思想可以来区分生物学中的一些概念,如激素、酶和蛋白质三者之间的关系,组成生物体的各类元素,细胞的结构,种群和群落,生态系统的成分和类型,生存斗争、种间斗争和种内斗争等。其次,有些计算中数量关系较为复杂,巧用集合图形,可以直观而简洁地解决这些问题,如遗传病的概率计算等。
1.1 基本概念辨析中的应用
【例1】人体是由细胞、器官、系统组成的统一体,下列能正确反映这四个概念之间关系的是 ( )
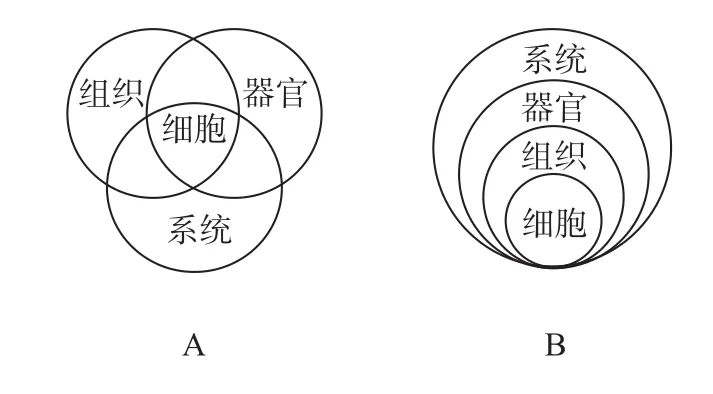
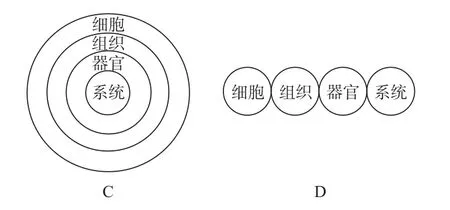
【解析】此题利用集合图能一目了然地展示生命系统的结构层次。
【答案】B
1.2 遗传病患病概率计算的应用
【例2】一对夫妇的后代若仅考虑一种病,患甲病可能性为a,正常的可能性为b;患乙病可能性为c,正常的可能性为d。他们只患一种病的可能性有以下几种表达方式,其中正确的是 ( )
①ad+bc ②1_ac_bd ③a+c_2ac ④b+d_2bd
A.① B.①② C.①②③ D.①②③④
【解析】本题主要考查遗传病中概率的计算。根据题意,结合集合中的交集、补集等思想,作出下图:
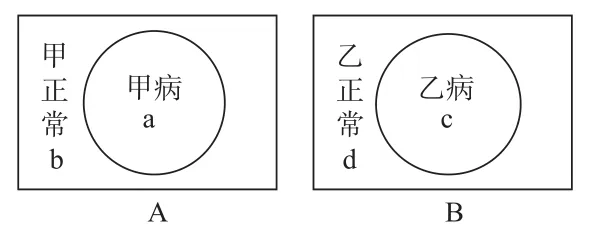
图1
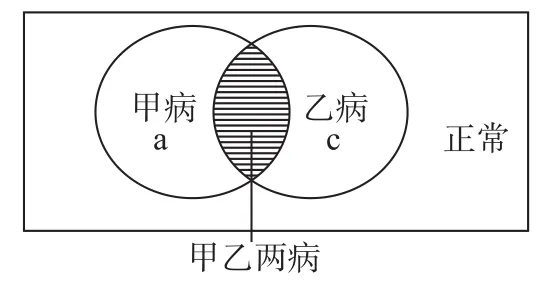
图2
从图1中A中可以看出,患甲病的概率为a 或(1-b),甲正常的概率为b或(1-a);从图1中B可以看出,患乙病的概率为c或(1-d),乙正常的概率为d或(1-c)。则患一种病的概率为1-ac(甲乙两病)-bd(正常)或ad(只患甲病)+bc(只患乙病)=(1-b)d+(1-d)b =b+d-2bd,从图2中可以看出患一种病的概率:a+c-2ac。故①②③④均正确。
【答案】D
2.数形结合思想
数形结合的思想,其实质是将抽象的数学语言与直观的图形结合起来,使抽象思维和形象思维结合,通过对图形的认识,数形结合的转化,使问题化难为易,化抽象为具体。以一道选择题为例,简单地分析此种思想在实际解题中的应用。
【例3】用32P标记了玉米体细胞(2N=20)的DNA分子双链,再将这些细胞转入不含32P的培养基中培养。在第二次细胞分裂的中期、后期,一个细胞中的染色体总条数和被32P标记的染色体条数分别是 ( )
A.中期20和20、后期40和20
B. 中期20和10、后期40和20
C. 中期20和20、后期40和10
D. 中期20和10、后期40和10
【解析】本题主要考查DNA分子的半保留复制。单纯靠理解,解题比较困难,但以一对同源染色体为例结合有丝分裂的图像,画出如下所示的图像,则一目了然。
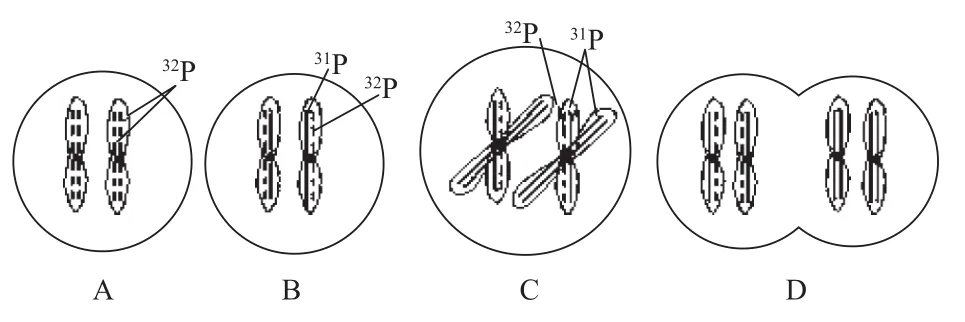
假设图A是一个正常的玉米体细胞,经过第一次有丝分裂形成的子细胞为体细胞(图B);在第二次有丝分裂的中期、后期分别为图C和图D。从中可看出,被32P标记的染色体条数分别为20条和20条。
【答案】A
3.极限思想
所谓极限思想,是指用极限概念分析问题和解决问题的一种数学思想。借助极限思想,可将某些生物学问题化难为易,避免一些复杂运算,探索出解题方向或转化途径。
【例4】下图中曲线能正确表示杂合子(Aa)连续自交若干代后,子代中显性纯合子所占比例的是 ( )
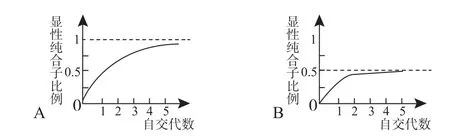
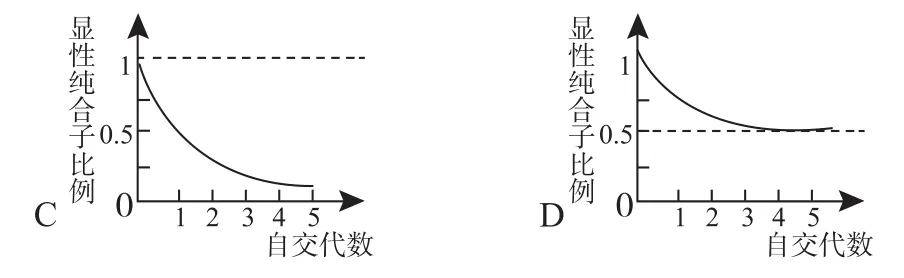
【解析】正常解法:杂合子自交n代,Fn中显性纯合子的比例为杂合子(Aa)连续自交1代,即n=1,代入即可计算出F2中显性纯合子的比例杂合子(Aa)连续自交2代,即n=2,代入即可计算出F2中显性纯合子的比例;杂合子(Aa)连续自交3代,即n=3,代入即可计算出F2中显性纯合子的比例依此类推,杂合子(Aa)连续自交n代,则F2中显性纯合子的比例接近
极限法:根据题意,经遗传图解分析可知:Aa自交一次,后代中杂合子(Aa)占1/2,纯合子占1-1/2=1/2;自交二次,后代中杂合子占1/4,纯合子占1-1/4;……依次类推,可设Aa自交n次后子代的显性纯合子的比例为y,则2y=当n→∞时,y→1/2,随着自交次数的不断增加,后代显性纯合子的比例越来越高;当自交的次数趋于无穷大时,后代基本都为显性纯合子和隐性纯合子。
【答案】B
综上所述,在生物学的某些问题的处理上,如果能借助数学思想,将会使复杂的问题简单化,抽象的问题直观化。此外在解决某一具体问题时,可单独运用某种数学思想或多种数学思想并用。总之,解决了问题,突破了难点,就是成功者。

甘肃省平凉市华亭县华亭一中)