船舶轴系校中计算方法分析

周广岭

摘 要：本文从建立船舶轴系对中计算坐标系开始，分别介绍三弯矩法、传递矩阵法、有限元法三种计算方法的基本原理及其要点，并对三种方法进行简要的比较分析。

关键词：轴系；校中计算；分析

中图分类号：U664.2 文献标识码：A

Ships Shafting Alignment Calculation Methods

ZHOU Guangling

（ Guangzhou Shipyard International Co.， Ltd. Guangzhou 511462 ）

Abstract： Starting from building coordinate system for ships shafting alignment calculation， this paper introduces the basic principles and key points of the three-moment， transfer matrix and finite element methods of the shafting alignment calculation respectively， compares and analyzes the three methods briefly.

Key words： Shafting； Alignment calculation； Analysis

1 前言

目前軸系校中计算方法基本都采用静态校中方法，它假定轴系各个轴承为刚性支点，推进轴系视为刚性铰支上的连续梁。其使用较为广泛的计算方法有三种：三弯矩法；传递矩阵法；有限元法。

2 坐标系及模型的简化处理

2.1 坐标系的建立

选取船舶螺旋桨末端作为坐标系原点；选取船舶校中轴系的理论中心线作为x轴，其正向指向船首；过原点垂直x轴的作为z轴，其正方向向上；规定y轴以面向船首指向右舷为正方向。由XOZ组成的平面，称为XZ平面或垂直平面；由XOY组成的平面，称为XY平面；XZ平面上各参变量的符号与正方向规定，见图1；XY平面上各参量的正方向规定，同XZ平面。

P集中载荷；q均匀载荷；Zb轴承变位；θ轴截面转角；Qi轴截面剪力（i=1，2，3）；

M1、M2弯矩；m外加力偶；Ri轴承支反力（i=1，2，3）

图1 轴系校中计算

2.2 实际轴系的简化处理

在船舶轴系校中计算过程中，需要对船舶轴系进行相关的假设和简化，通常将船舶轴系简化成连接在一个刚性绞支架的连续的梁部件。对于尾轴、中间轴、推力轴和减速齿轮箱等大构件的自重，简化为均布载荷处理；对于桨轴螺母以及轴套简化为均布载荷处理；对于船舶尾轴浸水和浸油的轴段，需要考虑水或油产生的浮力对轴段的影响。若轴段浸油则取自身重量的90%，而轴段浸水则取自身重量的87%。

作用在船舶轴系上的载荷，如螺旋桨、推力盘和大齿轮等，其与相应的船舶轴系轴段等轴径部分，则简化为均布载荷进行处理。

（1）船舶螺旋桨的简化处理

在船舶轴系校中计算中，通常把螺旋桨重量简化为集中载荷来处理；而船舶航行时，则还需要考虑水浮力对其的作用影响。

① 若船舶螺旋桨全部浸入水中，则其重量按下式计算：

（1）

式中：Wp—轴系中螺旋桨重量，（N）；

Wa—船舶螺旋桨重量，（N）；

ρp—船舶螺旋桨密度，（kg/m3）；

ρsw —海水密度，（kg/m3）。

在一般情况下，允许取近似值为：Wp= （0.869～0.817）xWa

② 若船舶螺旋桨部分浸水时，则其重量按下式计算：

（2）

式中：Wsw —船舶螺旋桨浸水重量，（N）；

Wns —船舶螺旋桨自身重量，（N）；

在一般情况下，允许取近似值为：Wp =（0.935 ～ 0.947）x W

船舶螺旋桨的重量作用点的选取，一般情况下，取其桨叶中心线0.7R处和船舶螺旋桨轴线的垂直交点位置，或是取螺旋桨桨毂中心点的位置。

（2）轴系浸水与浸油的简化处理

在轴系校中计算中，应考虑轴系浸入滑油和浸入水中的影响。通常，对于船舶轴段浸入滑油的情况，可取船舶螺旋桨自身重量的90%；对于船舶轴段浸入海水的情况，可取船舶螺旋桨自身重量的87%。

（3）船舶大齿轮轴、中间轴、尾轴等的简化处理

在轴系校中计算中，对于其中的推力环、减速大齿轮、飞轮以及各个连接的法兰，通常作均布载荷或集中载荷处理。当采用集中载荷处理时，应取和其相对应的船舶轴段等轴径的轴段；若采用均布载荷处理时，其另外轴段选用集中载荷来简化处理。而且在采用载荷计算过程中，应取推力环、齿轮中横剖面、飞轮或者各对轴法兰的连接截面和轴系轴线的交点作为选取点。

（4）主机曲轴的简化处理

在对船舶主机进行简化处理时，认为主机曲轴和主轴颈为光滑的等轴径的轴，并且按均布载荷处理。十字头、连杆活塞以及主轴颈等进行往复旋转的部件，其质量都简化为集中载荷处理并叠加在与之相对应的曲柄销轴的中心位置。其实对于船舶主机内各气缸的运动部件质量，有些主机服务商建议不考虑，而是通过把主机内的曲轴简化为变直径的均匀轴段来处理。

（5）各轴承支点的选择

船舶轴系校中计算中，应考虑船舶螺旋桨悬臂的影响作用，进而使轴系中轴承实际承压中心往后推移。

对于尾轴后轴承的支点空间位置的选取，各个船级社有着不同的规定：endprint

英国船级社（LV）建议：若尾轴后轴承是铁梨木，支承点取离轴承后端（1/3～1/4）S处；若尾轴后轴承为白合金轴承，则取（1/3～1/2）S。其中S为尾轴承的长度。

法国船级社（BV）建议：若尾轴后轴承是铁梨木，支承点取离轴承后端（0.5～0.8）D处；若尾轴后轴承是白合金轴承，则支承点取离轴承后端0.5D处。其中D为轴径。

美国船级社（ABS）建议：若尾轴后轴承是白合金轴承，其支点取离轴承后端 D处。其中D为轴径。

3 三种轴系校中计算方法

3. 1 三弯矩法

（1）三弯矩方程

如图2所示，三弯矩方程如下：

（3）

式中：Ii—第i及i+1支承间的跨距，（m）；

Mi—第i个支承截面的弯矩值，（Nm）；

Ei—第i及i+1支承間船舶轴段的杨氏模量值，（N/m2）；

qi—第i及i+1支承间船舶轴段所承受的均布载荷值，（N/m）；

Zi—第i轴承截面挠度值，（m）

（2）改进的三弯矩方程

（4）

（3）各个实支承的支反力 R；

（5）

（4）第i个截面处的转角θ；

（6）

（5）第i节点处左、右截面剪切力QiA、QiB

（7）

QiB=QiA+Pj+Ri（j=1，2，3…） （8）

如考虑其剪切变形的影响，则三弯矩方程可按公式（9）和公式（10）求解：

（9）

（10）

式中：G -材料的剪切模量，（N/m2）；

Ai -第i个支承处的截面面积，（m2）；

Asi -有效剪力面积，可近似取ASi=A，（m2）；

asi -剪力系数。

3.2 传递矩阵法

传递矩阵法，就是在结构静力学的线性理论的基础上，在结构中选取两个相邻截面的状态矢量值，利用线性变换矩阵进行相互连系。传递矩阵法是可借用计算机求解的数值算法，无论是离散还是连接系统都可用传递矩阵法计算求解，其实质就是把轴系中每个梁单元中的相邻的位移和力信号表示为状态矢量，并借用跨间矩阵把两者紧密的连接起来。

采用传递矩阵法对船舶轴系进行校中计算时，应将船舶轴系按一定规律划分成有限个的弹性单元和惯性单元相连接的梁结构，每个单元都有两个端面，每个单元端面利用传递矩阵把相邻单元的状态矢量联系起来，并且计算出他们之间的关系方程式。而后可根据需要给定边界条件，列出各端面的状态矢量以及矩阵形式，对其求解得出结果。

如前所述，在建立轴系校中模型时，将船螺旋桨末端作为坐标系原点，规定x轴正方向为船首的指向，y轴的正方向为右舷方向，z轴正方向为垂直向上。船舶轴系在x—z平面内，其弯曲状态及轴段端面的应力和应变状态，都可由垂直位移z和截面转角θ、弯矩M以及剪力T表示，其向量形式为：

（11）

式中：Zi - 截面的状态矢量；n -角标。

船舶轴段单元左、右截面的状态矢量，则其矩阵进行传递方程为：

（12）

式中：ti -第i轴段的迁移矩阵；L -第i轴段的左角标值；R -第i轴段的右角标值。

（1）均布载荷的传递矩阵

当轴系收到如轴系自身的重力时，可简化为单元受均布载荷，如图3所示。其单元的传递矩阵的行列式，如式（13）。

（13）

式中：li -第i轴单元的长度；

qi -第i轴单元的均布载荷值；

Eli -第i轴单元的抗弯刚度。

（2）集中质量的传递矩阵

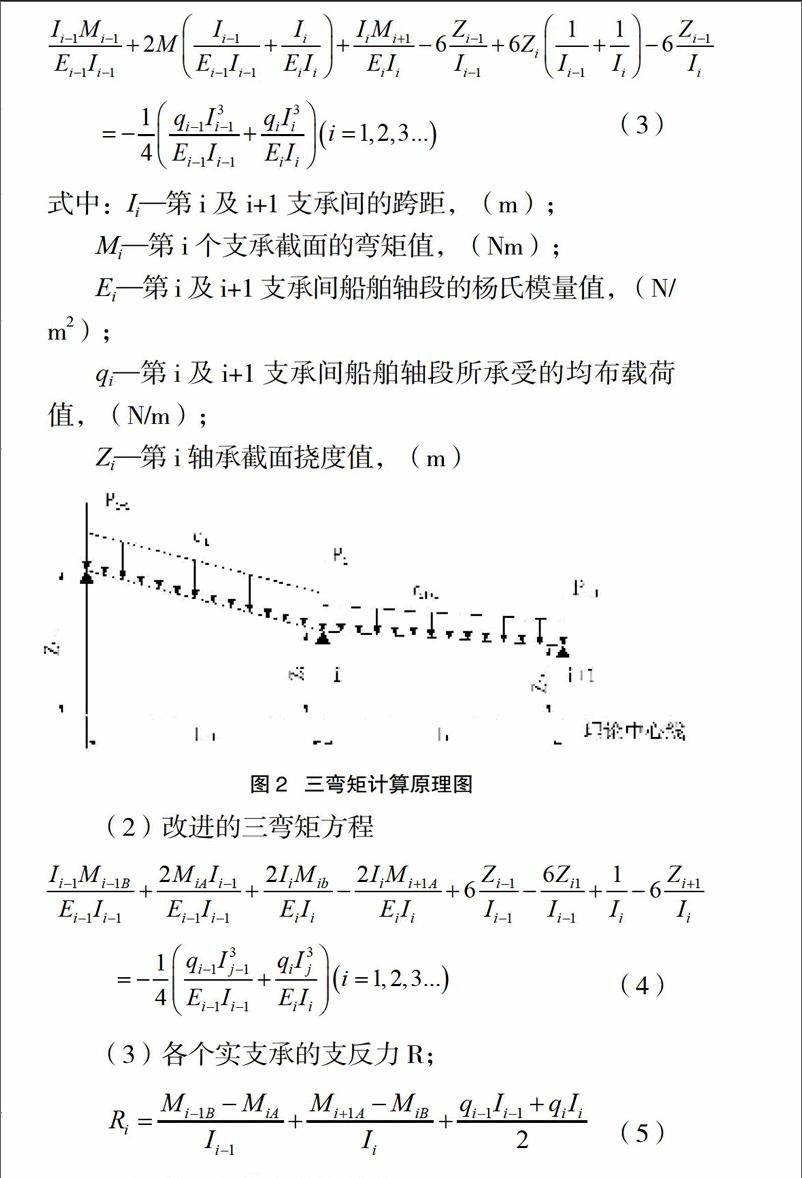
对于船舶轴系中的螺旋桨和主机内部的部件，通常将这其简化为集中载荷。假如在轴系动态校中计算中，需要考虑船舶主机气缸内的燃烧爆发压力和运动部件的惯性激振力的话，则对于这样爆发气压只需简化考虑某时刻即可，则得到的传递矩阵的行列式如式（14），受力模型如图4所示。

（14）

式中：Pi—表示船舶轴系中第i个轴单元的集中载荷。

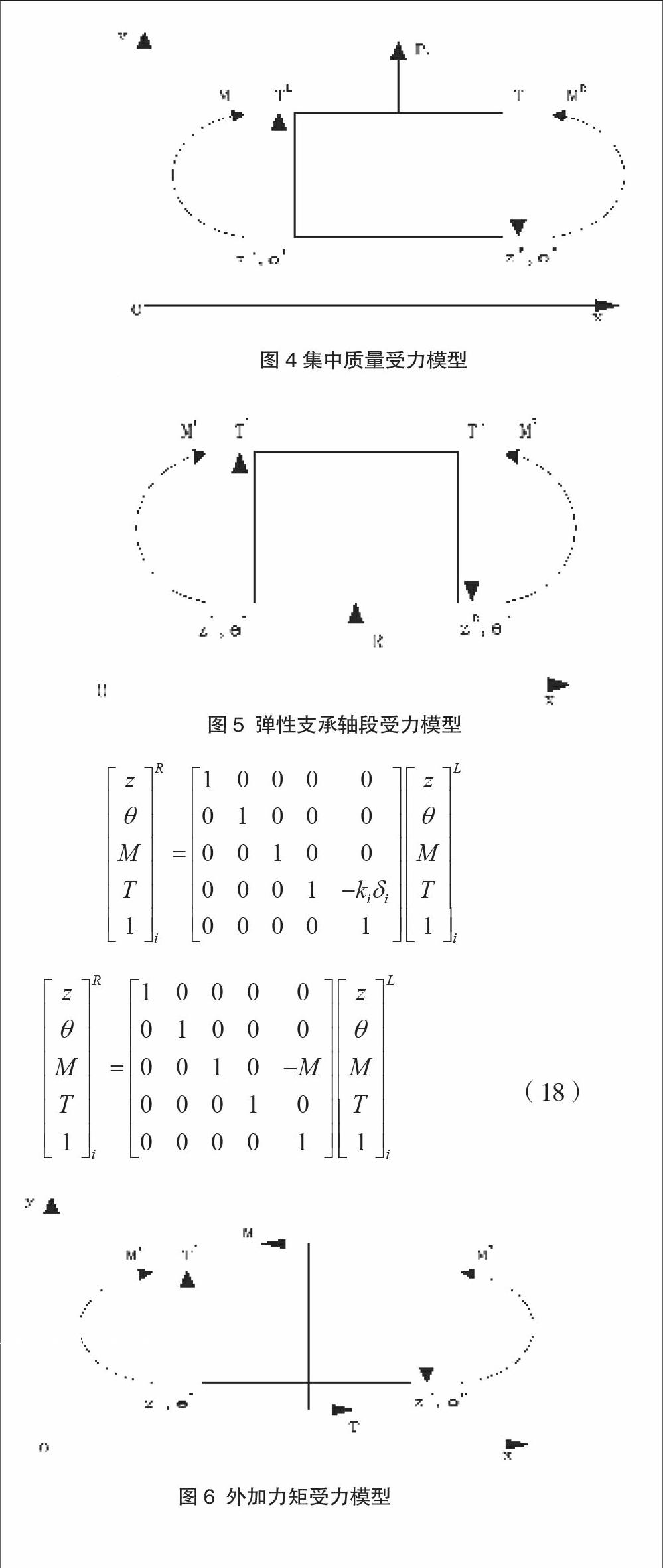
（3）弹性支承点的传递矩阵

将船舶轴系简化为若干个弹性支承单元的连续梁，如：主机各个主轴承、中间轴承、尾轴管前轴承、尾轴管后轴承。然后采用顶举法进行测量各轴承的负荷。所以在计算时应考虑轴系中支承等效刚度ke的计算影响，可由下公式得到：

（15）

式中：k0为轴承刚度，ks为船体刚度。

另外，还应考虑润滑油在轴承内形成的具有一定刚度的润滑油模，故等效刚度ke'公式为：

（16）

式中：k0为轴承油膜的刚度。

在安装时，中间轴需设置临时支承轴系，其受力模型如图5所示，矩阵的行列式，如式（17）：

（17）

式中：ki—第i支承单元简化的等效刚度，动态时取ke'，在静态时取ke；

δi—第i单元的z轴位移量，或由温差引起的垂向位移和船体变形。

在图5中， ，由于 ， 表示为在第i支承单元处没有支承时船舶轴系的垂向位移量。

（4）外加力矩的单元传递矩阵

船舶在正常航行过程中，螺旋桨在伴流场中运行，会促使船舶轴系受到一个垂向力和弯矩的作用。而且，其实际船舶轴系还会受到简化后的集中载荷、均布载荷作用和支反力，同时也会受到外界环境的影响，承受外力矩的作用，这就要求改进型传递矩阵另外加上一个外加力矩矩阵，以到达轴系合理校中并优化计算。因此基于传统传递矩阵之上，再外加力矩传递矩阵，其行列式如式（18）。外加力矩的受力模型如图6所示。endprint

（18）

式中：M—第i单元节点的外加力矩值。

采用传递矩阵进行轴系校中计算与三弯矩法计算比较可以发现，传递矩阵法的轴系校中结果更为准确合理，其计算过程中不仅克服了三弯矩法的缺点，而且可以对主机的激振力、温度影响以及螺旋桨水动力等因素进行合理简化计算，使其计算结果更加合理。

3. 3 有限元法

有限元法是将结构按一定规律离散为有限个相互关联的单元组合体，把存在一个无限多自由度且连续的复杂问题简化为一个简单可以求解的数值分析方法。由于有限元法在前期结构分析和静力求解工程应用中，取得了很好的成果并得到业界的认可

且随着计算机运算能力的快速发展，可以更加快速的解决离散化的数值分析，减少计算时间，故有限元法得到了快速的发展和推广。目前面向工程的有限元软件有很多，如ABAQUS、COMSOL和ANSYS等，這些软件操作简单、计算精度高，被船级社和业界广泛认可。

4 结束语

就目前对轴系校中方法的研究来说，有限元法对解决大多数复杂结构、复杂状况下的轴系校中问题具有很大的优势，尽管有限元法比三弯矩法及传递矩阵法的发展起步晚，但由于其能较好的处理船舶建造中遇到的复杂结构、复杂边界条件和复杂作用载荷等问题，并且其计算结果精度高、可行度大，故得到了迅速的推广和应用。

国内外的专家学者对船舶轴系校中算法不断研究完善，更甚应用三种方法相互结合进行计算，并且引用单目标线性规划、多目标线性规划的算法，取得了优于预期的结果。但尽管如此，轴系静态校中还是存在不足之处，它无法贴近船舶航行过程中轴系实际运转的工作状态，而轴系动态校中技术能更好的贴近轴系实际工作状态，其分析结果应更加合理，因此船舶轴系动态校中技术将成为船舶轴系校中的主要研究方向之一。

参考文献

[1] 程海明，又青，周瑞平.轴系校中的传递矩阵方法及其VB实现[J].武

汉理工大学学报，2003.27（4）.

[2] 耿厚才.船舶轴系动态校中计算[J].中国造船，2006（3） .

[3] 徐立华.传递矩阵法在船舶轴系校中计算中的应用[J]..武汉船舶职业

技术学院学报，2002（4）.

[4] 周继良， 邹鸿钧. 船舶轴系校中原理及其应用[M]. 人民交通出版社.

1985.endprint