没水倾斜板式防波堤消波性能分析
2017-12-11王禹龙上官子昌董榅键
王禹龙,上官子昌,董榅键,祁 隆
(大连海洋大学 海洋与土木工程学院,辽宁 大连 116023)
没水倾斜板式防波堤消波性能分析
王禹龙,上官子昌,董榅键,祁 隆
(大连海洋大学 海洋与土木工程学院,辽宁 大连 116023)
提出了一种将波浪中倾斜板问题等效化简为波浪中水平板单元组的方法,该方法建立在使用分离变量法求解水工结构边值问题的基础上,并使用伽辽金法精确求解连续边界条件,确定考虑衰减波态的速度势函数,从而求解没水倾斜板结构的消波性能。等效化简法计算精度于边界元法相当,且计算单元数量少、开销低。基于二维线性势波理论,对没水倾斜板式防波堤消波性能分析显示,没水板的倾斜角度、没水深度与板长是结构消波性能的控制因素:没水倾斜板防波堤的消波性能优于没水水平板防波堤的消波性能,随着没水板结构的倾斜角度增大,没水倾斜板结构的波浪透射系数显著减小,且长板优于短板,浅板优于深板;与前人的水槽实验对比显示,相对没水深度与波陡影响结构的消波性能,且波陡造成的波浪破碎贡献了显著的波能消耗。该结论对板式防波堤的结构配置、优化设计有重要意义。
等效化简;特征展开;伽辽金法;倾斜板;潜堤;消波
近年潜没于水面下的板式防波堤在近海海域中的应用越来越广泛。建设于日本静冈县清水区的CALMOS结构(Calm Offshore Structure,有脚式消波构造物)为多层水平板结构[1-2],其养护沙滩的效果十分明显;建设于日本北海道网走湖的倾斜板式防波堤不仅能适应潮位变化,也能有效提高渔港内的水面静稳度[3-4]。板式防波堤具有诸多优点:环境友好,适应大波高、大水深、弱基础,施工快,易维护。倾斜板式防波堤不仅继承了水平板式防波堤的优点,而且能适应潮位变化,从而提高了该结构作为防波堤的可行性。
与没水平板理论与实验分析相比,没水倾斜板的研究从时间与规模上都较为滞后。青山哲也等[5]利用非定常缓坡方程与伯努利定律分别分析了没水倾斜板周围自由水面流域与板下流域的水面变动与流量,基于微小振幅波理论并利用平板端部连续性边界条件求解没水倾斜板的波浪反射系数;并通过水槽实验给出了没水板结构在不同波陡与相对水深下的消波性能关系;倾斜板对较小波长,较高波陡波浪的消波作用更加有效。Parsons和Martin[6-7]利用超奇异边界积分方程求解半没水倾斜板的波浪散射问题。余锡平[8]对近海没水平板的消波效果与机理做了详细的总结并分析介绍了有关没水平板反射透射性能计算的方法,包括在随机波浪下、非线性波浪下各几何参数对没水平板的影响,并指出倾斜角度对板式防波堤的有效性尚不能确定。刘勇等[9]利用边界元法对没水倾斜板式防波堤进行数值分析,讨论了倾斜角度对反射系数与透射系数的影响,并证明了在相同的倾斜板角度的前提下,前倾或后倾对消波效果没有影响。随着对没水倾斜板式防波堤实验研究的深入,Rao等[10]和Yagci等[11]明确提出倾斜板式防波堤更优于水平板式防波堤的结论,这使得之前关于没水板式防波堤的倾斜角的有效消波效果变得明晰起来。
传统水平板式防波堤波浪消波性能分析的方法主要为特征函数展开法、边界元法和有限元法等。特征函数展开法又称领域分割法[12](the method of matched eigenfunction expansions)。简而言之,是将流体领域分割成矩形区域,相邻区域的速度势函数(代表波压力)与速度势函数的法向微分(波流速)满足连续性条件,利用特征函数正交性质建立关于未知系数的一次线性方程组求解。这里试图使用该方法并结合伽辽金法求解倾斜板的边值问题;在处理边界时,将倾斜板等效化简为一组水平板单元,随着水平板单元数量增加,其消波效果亦接近倾斜板的真实效果,如图1所示。
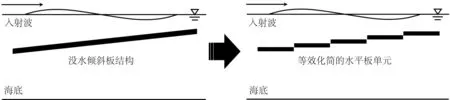
图1 有限水深中没水倾斜板等效化简示意Fig. 1 Conception sketch of simplified inclined plate
1 控制方程与边界条件
为不失一般性,基本计算模型如图2(a)所示,J段没水平板单元依次潜没于水深为h的波浪水域中,全部水域被划分为3J+1个区域:水平板单元长度(lj)、单元板厚(δj)、潜没深度(dj)与中点横坐标(xj)便能概括模型特征,其中j(j=1,2,3,……,J)代表水平板单元序号。

图2 等效简化倾斜板模型定义与水平板单元符号定义Fig. 2 Symbol definition for inclined plate model and single horizontal plate element in regions
倾斜板结构与等效化简的倾斜板模型参量关系:
其中,B为没水倾斜板水平方向投影长度,它与倾斜板原型的实际长度关系为B=Lpcosθ,下文称板长;D为没水倾斜板原型中点没水深度,下文称平均没水水深;θ为没水倾斜板原型与水平的夹角。
结构模型定义后,便是研究水域的变量定义。如图2(b)所示,任一水平板单元(单元编号定义为j),其水平长度中心点横坐标为x=xj,水平板单元左侧竖直边界为x=xj-lj/2,水平板单元右侧竖直边界为x=xj+lj/2。水平板单元左边界左侧的自由水面水域定义为区域1,水平板单元上侧自由水面水域定义为区域2,水平板单元下侧非自由水面水域定义为区域3,三个区域分别用符号定义为φ1,j,φ2,j与φ3,j。
考虑均匀水深h中入射波幅为A的波浪作用,基于线性势波理论,水体在流域内满足控制方程(4)与边界条件式(5)~(11)。


水平板单元边界条件:




二维辐射远场条件:
其中,ω为圆频率;k为入射波数;i为虚数单位。
以上边值问题求解可将速度势做特征值展开,在x=xj±lj/2处建立速度势函数与速度的跨边界连续方程。余锡平[13]对比分析了几种接合法,即选点解法、选段解法与伽辽金法。考虑最小化加权残差时,计算没水平板对波浪的反射表明伽辽金法最有效率,故以下利用伽辽金法求解。
2 速度势求解
2.1速度势函数一般解
对于自由水面区域与板下非自由水面水域Ω1,j,Ω2,j与Ω3,j,包含定常衰减波波态的速度势一般解可由线性化自由水面边界条件与分离变量法求解:
式中:Aj,n,Bj,n,Cj,n,Dj,n,Ej,n与Fj,n为一般解中待求未知系数;k0,n,kj,n与λj,n分别为自由水面区域,水平板单元上自由水面区域与水平板单元下非自由水面区域的复波数,其满足以下关系(15)~(17),可利用Newton-Raphson法计算。
以上复波数中,k0,0=-ik0,k0为实数色散方程的解,kj,0同理Εn(k0,nz),Ζn(kj,nz)与Λn(λj,nz)为特征方程(18)~(20)。
自由水面区域中,Ω1,1在x=-边界处、Ω1,J在x=+边界处衰减受阻;于是可轻易得到以下符合辐射条件的边界信息。
2.2建立并求解线性方程组
水平板单元与其他水平板单元的影响是相互的:迎浪侧水平板单元的透射波浪将以入射波浪传播入第二块水平板单元区域;第二块水平板单元区域的反射波浪将同样以反射波的形式传播入第一块迎浪侧水平板单元区域。表现在速度势函数中,即系数的相互影响的传递效果(如图3所示),入射波浪波高A1,n(n=0,1,2,3,……)受到第一块水平板单元作用,经C1,n(n=0,1,2,3,……) 的传递,影响到第二块水平板前入射波浪波高A2,n(n=0,1,2,3,……),此作用最终影响到透射波浪波高AJ+1,n(n=0,1,2,3,……);反射波高波浪BJ+1,n(n=0,1,2,3,……)受到最后一块水平板单元作用,经DJ,n(n=0,1,2,3,……)的传递,影响到前一块水平板前入射波浪波高BJ,n(n=0,1,2,3,……),此作用最终影响到反射波浪波高系数B1,n(n=0,1,2,3,……)。

图3 水平板单元系数传递示意(n=0, 1, 2, ……, N)Fig. 3 Effects over elements (n=0, 1, 2, ……, N )

图4 系数矩阵M结构图(J=3,N=1)Fig. 4 Diagram of matrix structure (J=3,N=1)
根据相邻区域的速度势函数,速度连续性条件与辐射条件,3J+1个水域可建立(6J+2)(N+1)元方程组,该方程组包含(8J+2)(N+1)枚等式。合并关于速度连续的方程组,可利用伽辽金法简化方程组,详细推导可从相关文献[14]得到。利用特征函数的正交关系最后得到包含(6J+2)(N+1)枚等式的(6J+2)(N+1)元线性方程组。
线性方程组的系数可以方阵形式列出,该方阵可利用Gauss-Jordan消元法求解,其结构如图4所示。图4表示了J=3时水平板单元组成的倾斜板问题的系数矩阵结构图,衰减波波态数量为N=1,图中每一枚实点代表矩阵中一个元素:三个水平板单元的小矩阵Mj(j=1,2,3)依次从上开始向下排列,最后为表示辐射边界条件的矩阵,故水平板单元矩阵Mj维度为6(N+1)×(6J+2)(N+1);辐射条件矩阵的维度为2(N+1)×(6J+2)(N+1)。其中每2行实点分别对应一枚等式中系数(见图4矩阵M2所示)中N=0与N=1两种衰减波情况,此方程组中有6(N+1)个公式,分别由水平板单元左侧竖直边界x=xj-lj/2与右侧边界x=xj+lj/2得到(见图4矩阵M3所示的上下两部分),故12行元素,16列亦如此,从左至右依次为Aj,Bj,Cj,Dj,Ej,Fj,Aj+1,Bj+1,其中J=3,N=1。
3 结果分析
3.1结果验证
通过线性方程组求解或矩阵计算,可得所有水域速度势函数,定义倾斜板对波浪的反射系数和透射系数如式(26)和(27)。并将计算结果与既往关于没水倾斜板的数值解数据进行比较,以验证该模型的有效性。
图5给出了没水平板结构对波浪的反射系数与透射系数理论结果,这与余锡平所得理论结果[8]吻合良好(h/L=0.25,d/h=0.30),其中微小的偏差是由于余锡平文中不计板厚度。
图6给出了没水倾斜板结构对波浪的反射系数与透射系数理论结果。可以看出,本结果与刘勇等[9]利用边界元法所得理论结果吻合良好(B/h=1.00,d/h=0.15,δ/h=0.1)。

图5 没水平板结构反射与透射系数(J=1, N=20)Fig. 5 Coeff. of submerged horizontal plate (J=1,N=20)

图6 没水倾斜板结构反射与透射系数(J=25, N=20)Fig. 6 Coeff. of submerged inclined plate (J=25,N=20)
3.2没水倾斜板的消波性能分析
图7给出了倾斜角度对没水倾斜板消波性能的影响(J=25,N=20,以下计算均如此),即没水板结构厚度δ=0.10h、平均没水水深D=0.15h、倾斜板长度与水深比B/h=1.00,没水倾斜板在不同倾斜角度下相对板长(B/L)的变化规律。没水倾斜板式防波堤的透射系数随着倾斜角度的增加,在不同相对板长情况均呈现出降低的趋势;特别的,相对板长为约0.15到0.30时能够形成最好的效果。这说明,增加倾斜角度有助于提高没水倾斜板的消波性能。
图8给出了没水深度对没水倾斜板消波性能的影响,即没水板结构厚度δ=0.10h、平板倾斜角度θ=15°、倾斜板长度与水深比B/h=1.00,没水倾斜板在不同没水深度下相对板长(B/L)的变化规律。没水倾斜板式防波堤的透射系数随着没水深度的增加,呈现出增大的趋势:没水深度越小,消浪效果越好,相对没水深度小于0.20时能够形成最好的掩护效果,更深的没水深度的消波效果急剧下降。这说明,没水深度的减小能够显著提高没水倾斜板的消波性能。
图9给出了倾斜板长对没水倾斜板消波性能的影响,即没水板结构厚度δ=0.10h、平均没水水深D=0.15h、平板倾斜角度θ=15°,没水倾斜板在不同相对板长随相对水深(kh)变化的规律。没水倾斜板式防波堤的透射系数随着板长的减小,呈现出增大的趋势,且相对板长为约0.80以上时能够形成最好的掩护效果,更短的板长结构的消波效果急剧下降。这说明,增加板长能够显著提高没水倾斜板的消波性能。

图7 倾斜角度对没水倾斜板消波性能影响(δ/h=0.10,D/h=0.15,B/h=1.00)Fig. 7 Inclination effect on submerged inclined plate breakwater(δ/h=0.10,D/h=0.15,B/h=1.00)

图8 没水深度对没水倾斜板消波性能影响(δ/h=0.10,B/h=1.00,θ=15°) Fig. 8 Submergence effect on submerged inclined plate breakwater(δ/h=0.10,B/h=1.00,θ=15°)

图9 相对板长对没水倾斜板消波性能影响(δ/h=0.10,D/h=0.15,θ=15°)Fig. 9 Length effect on submerged inclined plate breakwater(δ/h=0.10,D/h=0.15,θ=15°)

图10 相对板厚对没水倾斜板消波性能影响(D/h=0.15,B/h=1.00,θ=15°) Fig. 10 Thickness effect on submerged inclined plate breakwater(D/h=0.15,B/h=1.00,θ=15°)
图10给出了倾斜板厚对没水倾斜板消波性能的影响,即没水板结构平均没水水深D=0.15h、倾斜板长度与水深比B/h=1.00、平板倾斜角度θ=15°,没水倾斜板在不同相对板厚时相对板长(B/L)的变化规律。
在相对板长为约0.20以内时,没水倾斜板式防波堤的透射系数随着板厚的增大,呈现出减小的趋势,且在相对板长小于0.15左右时,厚板的消浪效果优于薄板。这一结论与刘鹏飞等[15]对淹没矩形箱式防波堤厚度对透射系数的影响可得到印证。
图11中曲线给出了没水倾斜板在板厚度δ=0.10h、倾斜角度θ=10°,不同相对波长与不同相对潜没深度时反射系数与透射系数与相对板长的关系;与此对照的是用点线表示出的青山哲也等[5]的实验结论。计算与实验的透射系数与反射系数在相对板长小于0.3时较好的符合,在此之后计算值均明显大于实验值;而且较大的波陡系数时亦如此,这一差异越来越大的趋势在透射系数上尤为明显。这种趋势说明倾斜板对较小波长波浪,较高波陡波浪的消波作用更加有效。相比于图11(a)、图11(b)中计算与实验更接近,即计算值在不同波陡的实验值上表现出相同的变化,而且差距不显著。这说明在该实验条件下,因为较大的没水深度避免了波浪在板上的破碎,使得其更接近数值计算的假设。

图11 没水倾斜板在不同相对水深下的消波性能Fig. 11 Measured and computed results of submerged inclined plate in relative water depth
4 结 语
通过将倾斜板等效化简为一组水平板单元,并结合伽辽金法匹配连续条件,得到了利用传统特征函数展开法对倾斜边界问题的半解析解,从而实现了对没水倾斜板式防波堤的消浪效果的分析。现有理论模型的计算结论与既有的理论解与数值解相互吻合良好,证明了该方法在解决没水倾斜板与波浪相互作用问题上的有效性。理论分析结论表明,没水倾斜板防波堤的消波性能优于没水水平板防波堤的消波性能,逐渐增大的倾斜角度,显著减小了波浪透射系数;没水倾斜板的板长与没水深度这两项因素的分析结论与水平板结构相似,即较大的相对板长与较浅的没水深度减小了透射系数,这是因为绝大部分波浪能量集中于自由水面附近而且板结构异化了由波浪产生流速并阻隔了水质点的震荡轨迹。进一步与既往实验的对比研究发现,潜没较深的倾斜板实验结论与理论计算结果极为接近,而潜没深度较浅、波陡较大的倾斜板实验结论与理论结果差别逐渐增大,并形成显著差别。该结论证明发生在倾斜板上波浪破碎主要是由没水深度与波陡决定的,且势波理论在求解没水倾斜板式防波堤消波研究存在部分局限。由此,合适的倾斜角度与显著的波浪破碎对没水板式防波堤结构改进有积极意义,以提高没水倾斜板式防波堤的工程可行性。
致谢:对东京海洋大学沿岸域工学研究室冈安章夫教授的启发与池谷毅教授在工程实例资料收集与程序编写时给予了宝贵的协助和指导,在此致以衷心的感谢!
[1] 戸田建設株式会社. 有脚式消波構造物 CALMOS[EB/OL].1991. http://www.toda.co.jp/tech/ecology/ecology_10.html. (TODA Corporation. Calm offshore structure[EB/OL].1991. http://www.toda.co.jp/tech/ecology/ecology_10.html. (in Japanese))
[2] OKUBO H, KOJIMA I, TAKAHASHI Y, et al. Development of new types of breakwaters[R]. Nippon Steel Technical Report, 1994.
[3] 青山和義, 鎌田彰, 玉置淳二, 等. 呼人漁港における傾斜板式防波堤の建設[J]. 海洋開発論文集, 1997, 13: 931-936. (AOYAMA K, KAMADA A, TAMAOKI J, et al. The design of breakwater by “PSR” at YOBITO Fishery Harbor [J]. Proceedings of Civil Engineering in the Ocean, 1997, 13: 931-93. (in Japanese))
[4] 全国漁港協会. ひと工夫した渔港构造物事例集 [M]. 東京: 全国漁港協会, 1997: 17. (National Association of Fisheries Infrastructure. Case collection of fishing port structures[M]. Tokyo: NAFI, 1997: 17. (in Japanese))
[5] 青山哲也, 泉宮尊司, 磯部雅彦, 等. 没水平板による波浪制御法に関する基礎的研究[J]. 海岸工学講演会論文集, 1988, 35: 507-511. (AOYAMA T, ISOBE M, IZUMAKIYA K, et al. Fundamental study on wave control method by submerged horizontal plate[J]. Proceedings of the Japanese Conference on Coastal Engineering, 1988, 35: 507-511. (in Japanese))
[6] PARSONS N F, MARTIN P A. Scattering of water waves by submerged curved plates and by surface-piercing flat plates[J]. Applied Ocean Research, 1994, 16(3): 129-139.
[7] PARSONS N F, MARTIN P A. Trapping of water waves by submerged plates using hypersingular integral equations[J]. Journal of Fluid Mechanics, 1995, 284: 359-375.
[8] YU X P. Functional performance of a submerged and essentially horizontal plate for offshore wave control: a review[J]. Coastal Engineering Journal, 2002, 44(2): 127-147.
[9] 刘勇, 谢璐琼, 姚卓琳. 淹没式斜板防波堤水动力特性的数值分析[J/OL]. 2011, http://www.paper.edu.cn/download/downPaper/201111-69. (LIU Y, XIE L Q, YAO Z L. Analysis on the hydrodynamic performance of a submerged inclined plate breakwater [J/OL]. 2011, http://www.paper.edu.cn/download/downPaper/201111-69. (in Chinese))
[10] RAO S, SHIRLAL K G, VARGHESE R V, et al. Physical model studies on wave transmission of a submerged inclined plate breakwater[J]. Ocean Engineering, 2009, 36(15): 1199-1207.
[11] YAGCI O, KIRCA V S O, ACANAL L. Wave attenuation and flow kinematics of an inclined thin plate acting as an alternative coastal protection structure[J]. Applied Ocean Research, 2014, 48: 214-226.
[12] 日本土木学会. 海岸波動: 波·構造物·地盤の相互作用の解析法 [M]. 東京: 海岸工学委員会研究現況レビュー小委員会, 1994: 331-339. (JSCE. Coastal wave motion: Analysis method of wave, structure, ground interaction [M]. Tokyo: Coastal Engineering Committee Research Review subcommittee, 1994: 331-339. (in Japanese))
[13] YU X P. Patching methods for the analysis of wave motion over a submerged plate [J]. Reports of the Faculty of Engineering, Nagasaki University, 1995, 25(44): 35-42.
[14] BREBBIA C A, DOMINGUEZ J. Boundary elements [M]. Boston: WIT Press, 1994: 22-31.
[15] 刘鹏飞, 郑永红, 王利生. 淹没矩形防波堤透反射系数特性研究[J]. 海洋学报, 2006, 28(5): 138-144. (LIU P F, ZHENG Y H, WANG L S. Reflection and transmission properties of submerged rectangular breakwaters [J]. Acta Oceanologica Sinica, 2006, 28(5): 138-144. (in Chinese))
Wave controlling performance analysis of submerged inclined plate breakwater
WANG Yulong, SHANGGUAN Zichang, DONG Wenjian, QI Long
(College of Ocean and Civil Engineering, Dalian Ocean University, Dalian 116023, China)
A method is proposed to simplify the problem of wave interaction with a submerged inclined plate structure as a group of submerged horizontal plate elements. The separation variable method and Galerkin method are employed to solve the boundary value problem around this hydraulic structure and to find the approximation of transboundary continuity solution. This method, an equivalent approximating method, has demonstrated quite excellent accuracy with a fair speed comparing with boundary element method. Based on the two-dimensional linear wave theory, the analysis of the wave controlling performance of the submerged inclined plate breakwater shows that the inclination, water depth and the length of the plate are critical factors. The wave propagation over the submerged inclined plate structure is significantly reduced, the long plate is superior to the short one, and the shallow submerged plate is superior to the deep one. The comparison with the previous experiments indicates that the smaller wave depth also influences the wave controlling performance, and the wave-induced wave breaking over plate contributes to the remarkable wave energy dissipation. The conclusion is of great significance to the structural configuration and optimization design of this type of plate breakwater.
equivalent simplification; eigenfunction expansions; Galerkin method; inclined plate; submerged breakwater; wave control
1005-9865(2017)06-0055-07
TV139.2
A
10.16483/j.issn.1005-9865.2017.06.007
2017-03-24
王禹龙(1989-),男,河北衡水人,港口工程助理工程师,主要从事近岸构筑物研究。E-mail:wangyulong.dlou.edu.cn@gmail.com
