预应力钢-混凝土组合连续箱梁的变形分析
2017-12-11肖勇刚
戴 业,肖勇刚
(长沙理工大学 土木与建筑学院,长沙 410114)
预应力钢-混凝土组合连续箱梁的变形分析
戴 业,肖勇刚
(长沙理工大学 土木与建筑学院,长沙 410114)
以3片钢-混凝组合连续箱梁的变形试验为基础,其中RC1为普通组合梁,PC2和PC3为预应力组合梁,并结合虚功原理和换算截面法,提出了一种考虑自重、堆载、预应力和开裂影响的钢-混凝土组合梁变形计算方法.试验结果表明:预应力对钢-混凝土组合梁的变形影响较大,且有效预应力越大,跨中挠度越小;对于普通钢-混凝土组合连续箱梁,可通过考虑滑移效应的刚度折减法考虑混凝土板开裂对变形的影响;分析得到的理论挠度与实测挠度吻合较好.
钢-混凝土组合连续箱梁;有效预应力;刚度折减法;换算截面法
钢-混凝土组合梁桥是指钢梁和混凝土桥面板由抗剪连接件连接成一整体而共同受力的桥梁结构形式,充分发挥了钢材和混凝土材料各自的力学性能[1].
近年来,随着我国桥梁建设的发展,钢-混凝土组合梁在我国桥梁和建筑结构建设中已得到了广泛的应用.国内外对组合梁的强度[2-3]、刚度[4]和连接件[5-6]的承载力等方面也做了一系列的研究.聂建国等人[7-8]主要对预应力钢-混凝土组合梁在正常使用极限状态下的变形进行了分析.建立了简化计算模型,在考虑相对滑移效应条件下,提出了负弯矩开裂区长度及预应力束内力增量的计算公式.薛伟辰[9]主要对钢-混凝土组合梁长期变形性能进行了研究,并分析了混凝土收缩徐变对预应力钢-混凝土组合梁长期变形的计算方法.谭文辉[10]等人根据现有的研究成果,在考虑混凝土的收缩徐变和抗剪连接件的滑移对影响挠度的影响因素,推导出了钢-混凝土组合梁非线性变形的计算公式.在上述文献中,总体上都侧重于简支结构,而截面形式往往也都是工字型截面,对组合连续箱梁从理论到试验都缺乏必要的研究.
本文依据预应力钢-混凝土组合连续箱梁试验模型,在短期荷载作用下,对预应力钢-混凝土组合连续箱梁挠度变形的进行理论分析.
1 基本理论
1.1 参考模型
本次参考模型为3片钢-混凝土组合连续箱梁桥模型,RC1为普通钢-混凝土组合连续箱梁,PC2和PC3为预应力钢-混凝土组合连续箱梁.混凝土强度等级为C40,钢箱梁采用Q235 C级钢材,厚度为8 mm,连接件采用13×50圆柱头栓钉,在上翼缘钢板单排布置,间距为150 mm,体内预应力束采用15.2-1860钢绞线.3片试验梁均采用重物进行均布对称堆载,加载龄期为28 d,试验梁的自重等效荷载为长期堆载为分3级加载.模型具体设计图纸如图1-图4所示,加载流程如图5和表1所示.

图1 预应力钢-混凝土组合连续箱梁桥模型示意图(mm)
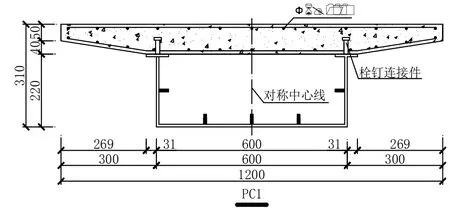
图2 RC1截面示意图/mm
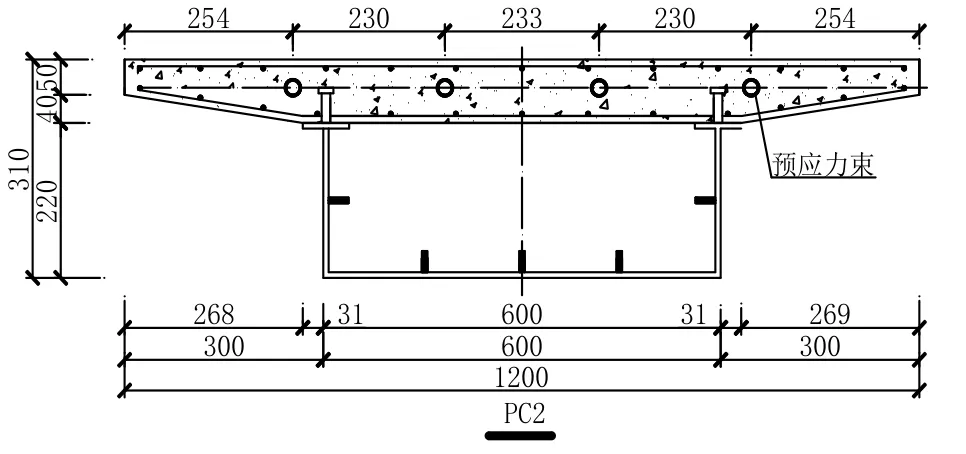
图3 PC2截面示意图/mm
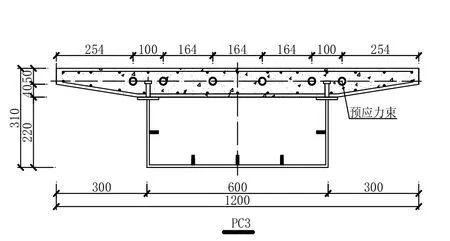
图4 PC3截面示意图/mm

图5 试验梁加载图
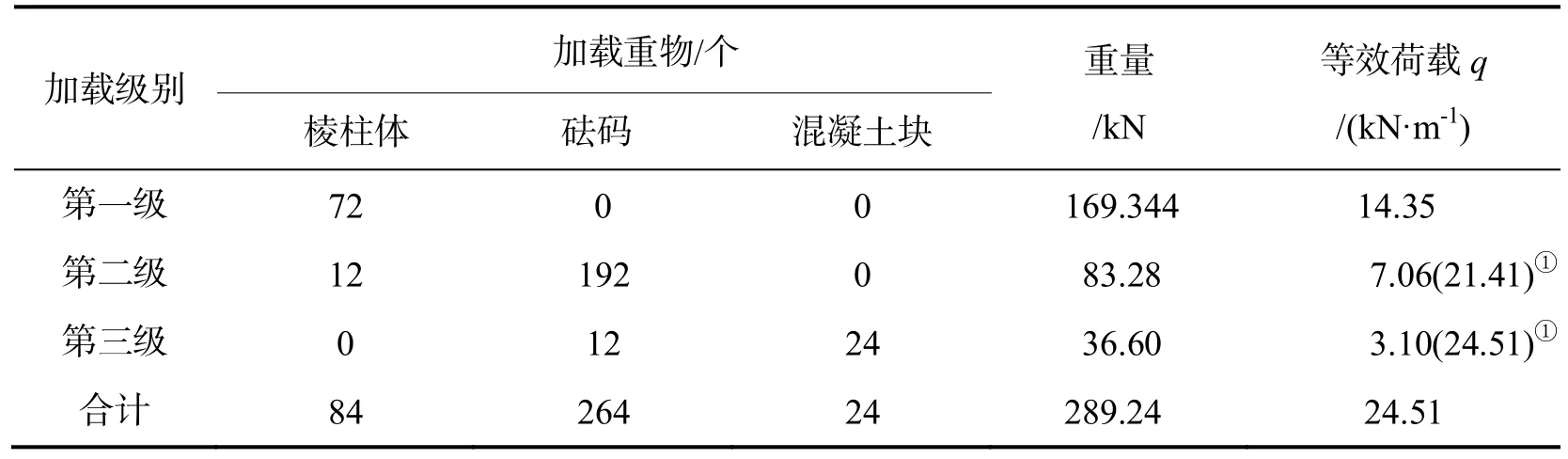
表1 试验梁分级加载表
1.2 基本假设
(1)不考虑剪切变形;
(2)预应力组合梁在堆载作用后始终处于弹性工作阶段;
(3)普通钢筋和混凝土之间无滑移;
(4)混凝土板与钢箱梁之间无掀起作用;
(5)预应力束的线型假设为直线型.
1.3 换算截面法
钢-混凝土组合结构由混凝土和钢梁两种不同性质材料组合而成,如图6所示.根据截面基本换算关系,将混凝土板截面和钢梁截面换算成等价的组合截面,并保证组合截面形心高度保持不变,即主轴的惯性矩保持不变,得出组合截面的基本特性,具体推导公式见式(1)-式(4).

图6 组合梁截面换算示意图
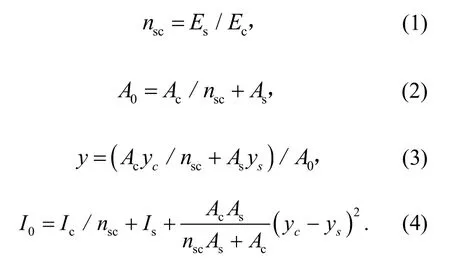
式中:Ec表示混凝土弹性模量,Es表示钢梁弹性模量,nsc表示钢梁弹性模量与混凝土弹性模量的比值;Ac表示混凝土板截面面积;As表示钢梁截面面积;A0表示换算后组合梁截面面积;yc表示混凝土板中性轴至顶板的距离;ys表示钢梁中性轴至底板的距离;y表示换算后组合梁中性轴至底板的距离;Ic表示混凝土板截面惯性矩;表示钢梁截面惯性矩;I0表示换算后组合截面惯性矩.
2 初始变形计算
在初始挠度计算中,预应力钢-混凝土组合连续箱梁在短期堆载作用后,仍处于弹性工作阶段,可按结构力学原理求解.在短期堆载和预应力共同作用下,预应力钢-混凝土组合连续箱梁截面弯矩为
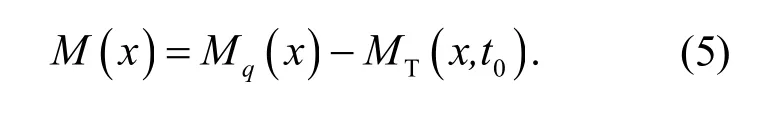
预应力钢-混凝土组合连续箱梁混凝土板截面初始应力可表示为
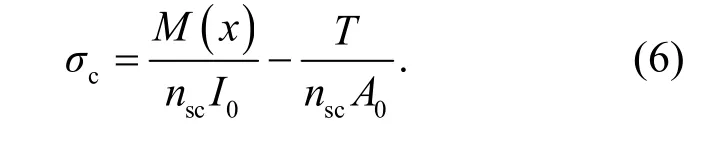
式中:T表示有效预应力,在普通钢-混凝土组合梁中取T=0.
其初始截面曲率为
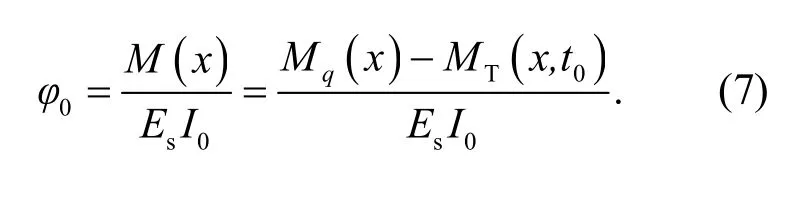
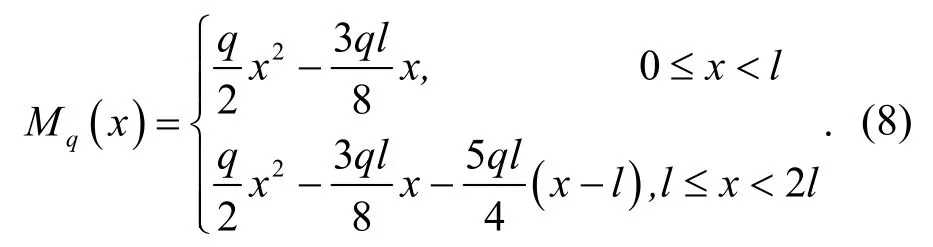
根据结构力学原理,可算出组合连续梁跨中初始挠度为
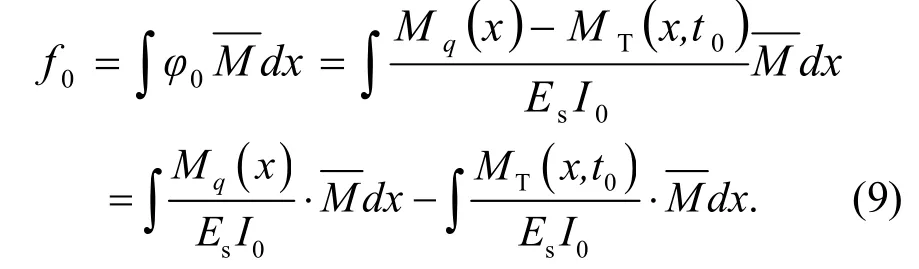
联合式(8)和式(9),取x=2/l可得跨中挠度为
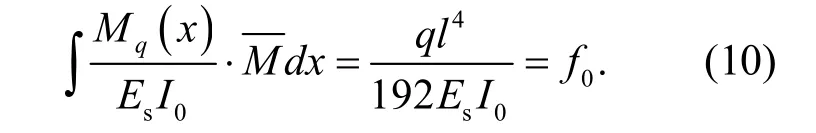
式中:f0表示在外荷载作用下非预应力2跨连续梁的跨中挠度.
由图1可知:预应力束仅布置在试验梁混凝土板负弯矩区段,布置线型为直线型,以中间支座为中心两边对称布置,总长度为5 000 mm,故可推导求出预应力引起的反拱挠度为
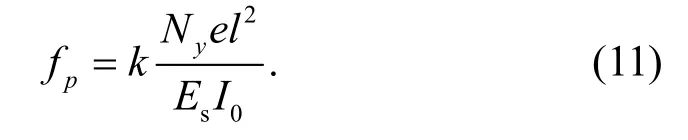
式中:fp表示预应力引起的反拱度;Ny表示有效预应力;e表示预应力束至中性轴的距离;l表示单跨计算跨径,本文取5 900 mm;k表示预应力线性引起的挠度系数,计算可取k=0.034.
对于普通钢-混凝土组合连续箱梁,在外荷载作用下,负弯矩混凝土板可能开裂导致截面刚度降低,而正弯矩处则不出现开裂问题.在短期加载过程中,负弯矩混凝土板裂缝的出现会导致混凝土板与钢箱梁产生相对滑移,组合梁沿长度方向刚度也将发生变化.故在普通钢-混凝土组合连续箱梁短期挠度计算中,可以对组合连续梁按考虑滑移效应的方法进行刚度折减,折减刚度B按文献[11]进行折减,具体为
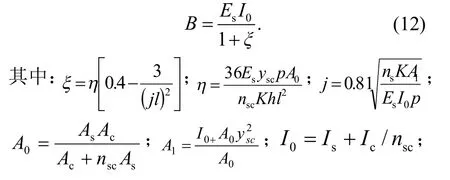
在得出了普通钢-混凝土组合连续箱梁的折减刚度系数后,可求出在短期荷载作用下,考虑负弯矩区段混凝土板开裂时的RC1短期挠度.对预应力钢-混凝土组合连续箱梁,在短期荷载作用下不出现裂缝,仍处于弹性工作阶段,PC2和PC3的短期挠度f2,3式(14)
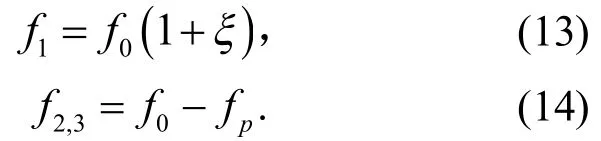
2.1 初始挠度对比
根据式(13)和式(14)得出了考虑负弯矩区段混凝土板开裂的普通钢-混凝土组合连续箱梁和预应力钢-混凝土组合连续箱梁在短期堆载作用下跨中挠度的计算公式,每级加载后试验梁挠度如表2所示.
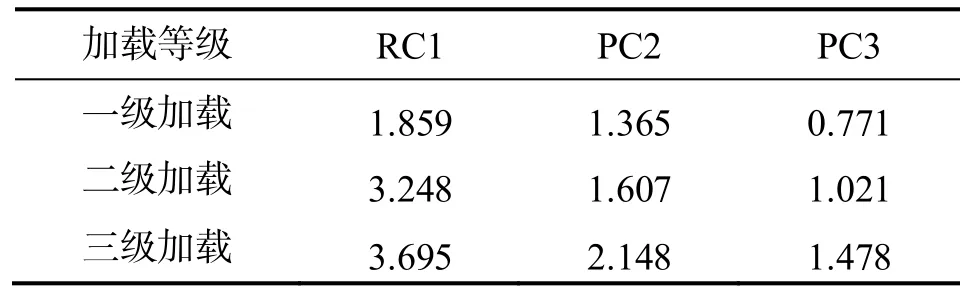
表2 试验梁加载过程中第一跨跨中挠度实测挠度/mm
通过理论计算与试验梁模型RC1、PC2和PC3的实测数据结果进行对比.
由图7-图9可知:从数据来看,PC2和PC3的理论数据分别较实测数据大了2.36 %和2.24 %,而RC1的实测挠度较理论挠度大了2.96 %.
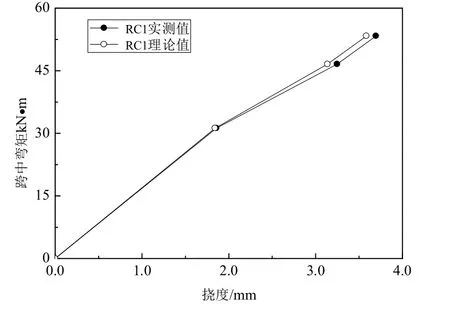
图7 RC1跨中截面挠度弯矩图
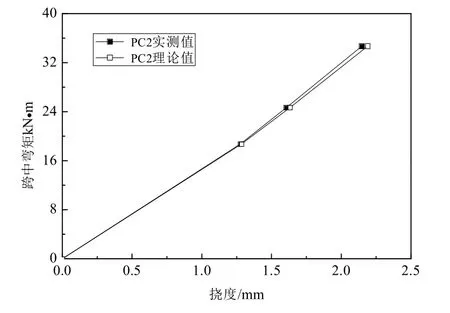
图8 PC2跨中截面挠度弯矩图
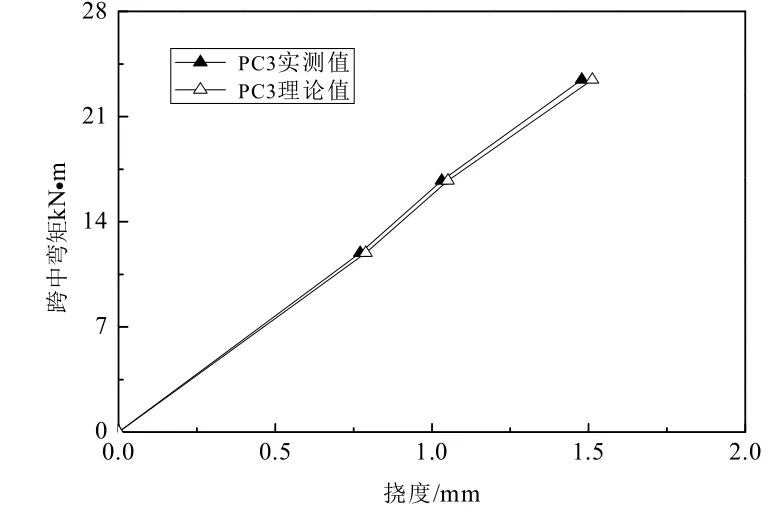
图9 PC3跨中截面挠度弯矩图
本次模型加载流程分为3次加载,RC1在加载后负弯矩区段混凝土板出现裂缝,导致截面刚度降低,挠度增长较大,故在2级和3级加载后,实测挠度较理论挠度偏差较大.PC2和PC3在加载后仍处于弹性工作阶段,跨中挠度理论值和实测值相差比较小,理论略大于实测值.RC1、PC2和PC3加载完毕稳定后的实测初始挠度分别为3.694 mm,2.148 mm和1.478 mm,RC1的初始实测挠度大于PC2和PC3,而PC3的挠度较PC2小了31.2 %.由此可知:预应力的施加可以有效的减小钢-混凝土组合连续箱梁的挠度,且施加的有效预应力越大,对挠度的抑制作用越明显.总体而言,两跨钢-混凝土组合箱连续箱梁的跨中挠度理论计算结果与实测试数据都较为吻合.
3 结论
通过短期堆载作用下的 3片钢-混凝土组合连续箱梁模型的理论变形分析,并结合了试验梁模型的实测挠度数据进行对比,得出结论如下:
(1)预应力的施加,会减小钢-混凝土组合连续箱梁的挠度的增长,且施加的有效预应力越大,对挠度的减小作用效果越明显.
(2)对于普通钢-混凝土组合连续箱梁负弯矩区段混凝土板开裂后的理论挠度计算中,考虑混凝土板与钢箱梁之间的相对滑移,对组合梁截面刚度进行折减,跨中挠度的理论结果与实测结果吻合较好.
[1]聂建国. 钢-混组合结构梁桥[M]. 北京: 人民交通出版社,2011.
[2]NIE J G, CAI S C. Steel-concrete composite beams considering shear slip effects[J]. Journal of Structural Engineering, ASCE,2003, 129(4): 495-506.
[3]钟新谷, 舒小娟, 沈明燕 等. 钢箱-混凝土组合梁正截面强度设计理论与试验研究[J]. 中国工程科学, 2008, 10(10): 47-51.
[4]张彦玲, 李运生, 樊健生. 钢-混凝土连续组合梁的刚度计算方法[J]. 中南大学学报: 自然科学版, 2013, 44(8): 3521-3526.
[5]余志武, 蒋丽忠, 李佳. 集中荷载作用下钢-混凝土组合梁界面滑移及变形[J]. 土木工程学报, 2003, 36(8): 1-6.
[6]李运生, 张彦玲, 樊健生. 钢-预应力混凝土组合梁滑移规律分析及连接件局部加强设计[J]. 工程力学, 2011, 28(1):192-198.
[7]聂建国, 陶慕轩. 预应力钢-混凝土连续组合梁的变形分析[J].土木工程学报, 2007, 40(12): 39-45.
[8]聂建国. 钢-混凝土组合结构-试验、理沦及应用[M]. 北京: 科学出版社, 2005: 211-217.
[9]薛伟辰, 孙天荣, 刘婷. 2年持续荷载下城市轻轨预应力钢-混凝土组合梁试验研究[J]. 土木工程学报, 2013, 46(03): 111-118.
[10]谭文辉, 李达. 钢-混凝土组合梁非线性变形研究[J]. 工程力学, 2008, 25(S1): 107-110.
[11]GB50017-2003, 钢结构设计规范[S].
(责任编校:徐赞)
Deformation Analysis of Prestressed Steel-concrete Composite Continuous Box Beams
DAI Ye,XIAO Yong-gang
(College of Civil Engineering and Architecture, Changsha University of Science amp; Technology,Changsha Hunan 410114, China)
Based on the deformation test on three steel-concrete composite continuous box beams, RC1 is an ordinary composite beam, PC2 and PC3 are prestressed composite beams, combining with virtual work principle and principletransformed-section method, a deformation calculation method was presented for steel-concrete composite beams considering the effect of dead load, surcharge load, prestressed force, and cracks. The results indicate that the prestressed force has greater effect on the deformation of steel-concrete composite beams, and the deflection decreased in higher effective prestressing. The effect of cracks can be considered by the method of stiffness reduction for ordinary steel-concrete composite continuous box beams.The theoretical deflection analyzed by the method proposed in this paper are in good agreement with the measured result.
steel-concrete composite continuous box beams; effective prestress force; stiffness reduction method; transformed-section method
TU41
A
10.3969/j.issn.1672-7304.2017.02.0008
1672–7304(2017)02–0033-05
2016-10-12
湖南省自然科学基金项目(14JJ4062)
戴业(1991-),男,湖南长沙人,硕士,主要从事钢-混凝土组合结构研究,E-mail: 664339367@qq.com;肖勇刚(1964-),男,江西南康人,博士,教授,主要从事结构非线性动力研究.
