铁路轨道不平顺波长及病害波形的定位方法
2017-12-11徐磊高建敏翟婉明陈宪麦
徐磊,高建敏,翟婉明,陈宪麦
(1. 西南交通大学 牵引动力国家重点实验室,四川 成都,610031;2. 中南大学 土木工程学院,湖南 长沙,410075)
铁路轨道不平顺波长及病害波形的定位方法
徐磊1,高建敏1,翟婉明1,陈宪麦2
(1. 西南交通大学 牵引动力国家重点实验室,四川 成都,610031;2. 中南大学 土木工程学院,湖南 长沙,410075)
应用时频分析和特征波形能量突变理论,开展轨道不平顺波长和轨道病害波形定位提取的研究。结合小波变换多分辨率分析和Wigner-Ville分布良好的时−频能量聚集性,提出基于小波−SPWVD的时−频能量波长定位提取方法,并与常规的尺度−小波能量谱方法进行对比分析。以时−频能量分析法为基础,基于轨道病害波形的统计特性,提出融合病害波形统计特征频率和频率影响系数的小波−SPWVD时−频能量病害提取算法,用于轨道病害特征波形的定位提取。研究结果表明:小波−SPWVD时−频能量分析方法和常规的尺度−小波能量谱方法在基本原理和定位提取性能上具有一致性与有效性,但时−频能量分析方法在时耗及特征波长信息含量上更具优势。用焊缝不平顺和凸台形不平顺的病害波形实例验证了时频能量分析方法的有效性。
轨道不平顺;小波变换;Wigner-Ville分布;特征波长;轨道病害
在铁路线路的运营、维护和管理过程中,以轨道不平顺峰值和标准差统计特性为基础的轨道几何形变处理模式已逐渐凸显不足,因此,必须考虑轨道不平顺波长对列车线路系统之间动力相互作用的影响,特别是在高速铁路线路中,由于行车速度高,轨道不平顺波长产生的附加动力作用更加明显。关于轨道不平顺不利波长、波长动力效应及融合轨道不平顺波长动力特性的线路管理方法的研究,已引起国内外研究者的广泛关注。练松良等[1]基于相干分析和功率谱分析方法,归纳出客货共运线路的轨道不平顺不利波长范围;徐磊等[2]提出轨道不平顺特征(不利)波长自动提取算法,通过离散小波变换自适应提取轨道不平顺和车体振动响应各频段特征不利波长;高建敏等[3]应用车辆−轨道耦合动力学理论,探讨了高速行车条件下轨道几何不平顺敏感波长问题;辛涛等[4]对200 km/h和250 km/h速度下轨道不平顺波长管理范围进行了探讨;王卫东等[5]借鉴能量集中率的思想,引入能量权系数表征不同波长成分不平顺对输入车辆/轨道系统总能量权重,提出一种综合评价车辆/轨道系统动态特性的广义能量指标;李再帏等[6]将轨道不平顺波长因素纳入轨道质量评价中,提出轨道质量的能量指标方法。上述研究表明轨道不平顺波长在铁路线路动力分析及维修管理中具有重要意义,对轨道不平顺不利波长进行有效控制与消除是一个亟待解决的问题。对轨道不平顺波长进行控制的前提是发现与定位波长。目前,采用频谱分析方法已能较好地提取轨道不平顺特征波长,但对于轨道不平顺波长和轨道病害特征波形的定位提取问题的研究相对较少。在实际工程中,往往由专门的技术人员根据轨道不平顺综合检测波形及个人经验进行波长及病害的提取,其检测效率及精度都存在一定的问题。本文作者综合信号时频分析和能量突变理论,提出一种基于轨道不平顺时−频能量分布的特征波长和病害波形提取方法,结合理论探讨、算法提出和实例计算验证该方法在波长及病害定位提取上的可行性。
1 时频分析基本方法
此前,国内研究者已对轨道不平顺进行时频分析,并取得一些初步的研究成果[7−9]。但研究深度还处于初步阶段,时频分析的基本方法也有限。因此,如何充分利用轨道不平顺信号的时−频处理结果,与现有的轨道评价分析方法、基础结构交互变形、实测或仿真动力响应等内容进行有效融合,提出一种统一的时−频域综合分析方法,都需要更深入地研究。本文针对轨道不平顺波长和病害的定位提取问题,对如何依据轨道不平顺的时−频域能量分布解决这一问题进行研究。
1.1 小波变换
小波变换法[10]可研究信号在各个时刻或各位置在不同尺度上的演变情况,实现了时频局部化分析。小波是具有震荡特性、能够迅速衰减到0的一类函数,即 ∫+∞ψ(t) d t =0。由ψ(t)的伸缩和平移构成一簇函数系:

式中:ψ(t)为ψ(t)的复共轭函数。在实际的工程应用中,信号一般为离散形式f(kΔt) (k = 1 ,2,···,N ;N为样本容量;Δt为取样时间间隔)。则式(2)的离散表达为

式中, Wψ,f(a,b)包含了 f (t)和ψa,b(t)的信息,因此小波函数的选择十分重要。目前广泛使用的有Haar小波,墨西哥帽(Maar)小波,高斯类小波,样条小波,Morlet小波等。将小波系数在时域或频域尺度进行能量展开,可获得相应的小波能量谱,其基本计算方法可参考文献[11]。
1.2 维格纳-威尔分布
维格纳-威尔分布(Wigner-Ville distribution,WVD)最早由维格纳(Wigner)提出[12],后经威尔(Ville)引入信号分析领域[13]。作为一种能量型时频联合分析,维格纳-威尔分布与其他时频分布相比有许多优点,如真边缘性、弱支撑性、平移不变性等[14]。信号 s(t)的瞬时自相关:
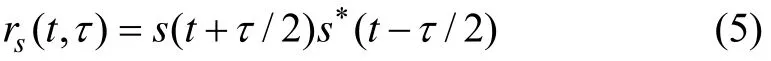
对式(5)进行傅里叶变换,得到WVD的一般表达形式:

由式(6)可知:WVD为信号的双线性表示,若某一信号能由其他 2个以上的信号表示,则此信号的WVD必然存在交叉干扰。在实际应用中,由于信号往往是离散的,若抽样周期为T,对连续时间信号 s(t)进行离散抽样,即 s(m T ) = s(t)|t=mT,利用Trapezoidal定理,则式(6)可改写为
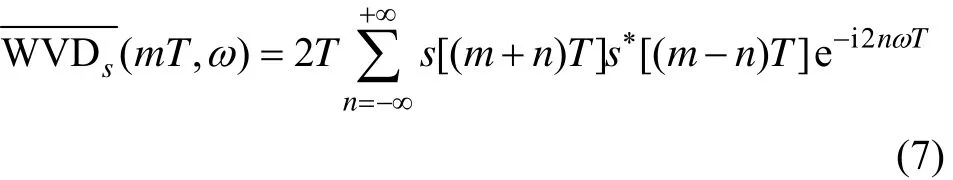
式(7)称为离散 WVD。本文采用平滑伪 WVD(即SPWVD)进行时−频能量分布的计算。
2 轨道不平顺波长定位方法
2.1 波长提取的基本原理
当信号中存在较为明显的特征频率时,特定频域尺度下的小波能量在此特征频率处将产生突变,且大于相邻频率的信号能量。若要检测某一特征频率,则可以提取信号时−频域联合能量分布矩阵中此频率对应的时域能量时程。另外,由于轨道不平顺幅值沿空间里程基本满足正态分布[15−16],根据正态随机变量超过其均值与3倍均方差之和的小概率原理,可设定相应的能量阈值用于判别轨道特征波长的存在,这些构成轨道不平顺波长提取的基本原理。
图1所示为基于连续小波变换和傅里叶变换的信号频率提取。图 1(a)所示为模拟的一段时域信号,具体计算公式如下:

其中:A1,A2和A3为幅值,分别为1,4和3 m。f1,f2和f3为频率,分别为4,20和30 Hz。w为加入的白噪声信号。图 1(b)和(c)所示分别为采用尺度−小波能量谱方法[11]和傅里叶变换方法进行信号的特征频率提取。由图1(b)可知小波能量谱方法能很好地提取信号中的特征频率。
2.2 基于尺度−小波能量谱的波长提取算法
针对轨道不平顺波长的定位和识别,可建立如下算法:

图1 基于连续小波变换和傅里叶变换的信号频率提取Fig. 1 Signal frequencies abstraction based on continues wavelet transform and F.F.T
1) 确定需要提取不利波长的路段,根据波长和采样率确定样本大小(则波长为 L,轨检车采样率为n点/m,则每个样本的点数为(nL+1)个);
2) 从第 M 个样本点开始,采用滑动检测方法每隔一定样本点数对轨道不平顺样本信号进行一次尺度−小波能量谱计算,提取对应波长下的小波能量谱值Ti(i=1, 2, …, m;m为样本数)。M主要用于初始能量阈值的计算。
3) 设定尺度−小波能量谱动态阈值 Ue,i,当 Ti>Ue,i, Ti-1> Ue,i-1且 Ti-2> Ue,i-2时,第 i - 1 个样本为较标准的基波型轨道不平顺。当提取了第 i -1个轨道不平顺波长后,下一个波长位置点应该至少在第i(n L+ 1 )个点之后。阈值 Ue计算公式如下:
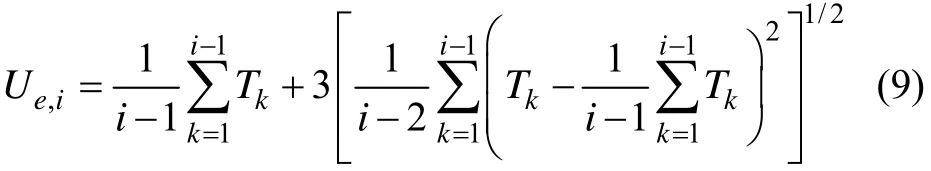
2.3 基于小波−SPWVD时频能量的波长提取算法
直接采用小波变换所提出的轨道不平顺波长(段)提取算法,其最大不足在于耗时、浪费计算资源,且无法进行时−频域联合分析。为此,通过小波−SPWVD联合分析方法获取轨道不平顺的时−频能量分布,直接从时−频能量分布中定位特征波长。基本算法如下:
1) 对轨道不平顺信号进行离散小波变换,根据需要提取的波长(段),选择特定的小波分解层重构信号;
2) 对重构信号进行SPWVD时频能量提取;
3) 在轨道不平顺的“空间里程(时域)−波长−信号能量”三维分布图中,提取波长(段)的时域能量分布“脊线”;
4) 直接设定能量阈值(见式(8)),从波长的能量分布“脊线”中定位波长。
2.4 算法比较与验证
随机选取武广高速铁路某500 m路段的轨道中心高低不平顺轨检数据来进行波长提取,如图2所示。
分别采用基于尺度−小波能量谱的波长提取算法和基于小波−SPWVD时频能量的波长提取算法,以6.5 m波长(即“特征波长”)为例,进行波长定位提取有效性的比较验证。其中,对于基于尺度−小波能量谱的波长提取算法,取 100M= ,每隔2个不平顺点计算1次样本的尺度−小波能量谱,特征波长尺度−小波能量谱值分布如图3所示。对于基于小波−SPWVD时频能量的波长提取算法,进行10阶离散小波变换,取第4阶近似重构信号的SPWVD时−频能量分布作为波长定位分析信号,如图4所示。由图4可知:第4阶细节重构信号的功率谱密度函数与时−频能量的频域能量密度平均值分布基本一致,均表现6.5 m这一特征波长。
取图 4(a)中特征波长对应的时域能量分布脊线作为特征波长的分析信号,如图5所示。
由图3和图5可知:采用尺度−小波能量谱方法和小波−SPWVD时−频能量联合分析方法,所提取的特征波长位置基本一致(特别是在300~400 m路段),只是稍有差别(如在图3的250~275 m区段,尺度−小波能量谱法显示此处存在6.5 m波长,而在图5中却没有表现出这一特征位置)。分析其原因,图5仅表现了第4阶重构近似信号的6.5 m波长分布特征,并未在其他的重构信号时−频能量分布中定位此波长,所以难免存在一定的漏检现象。基于图5所示定位结果,在图2原始数据中提取波形信号,如图6所示。其中图6(a)~(f)分别对应图5中①~⑥号特征波长。
由图6可知:所提取的信号波形基本满足6.5 m的波长特征,虽然并非严格服从正余弦波形分布,但从波形的延伸趋势来看,比较符合基频周期信号特征。

图2 原始轨道不平顺分布Fig. 2 Track irregularity series

图3 特征波长尺度−小波能量谱值分布Fig. 3 Scale-wavelet energy spectrum distribution of characteristic wavelengths

图4 第4阶细节重构信号的小波−SPWVD时频能量分布Fig. 4 Wavelet-SPWVD time-frequeny energy distribution of the 4th reconstructed detail signal

图5 特征波长小波−SPWVD时域能量分布Fig. 5 Wavelet-SPWVD energy distribution of characteristic wavelengths at time domain

图6 所提取的特征波长波形图Fig. 6 Waveforms of characteristic wavelengths
由上述分析可知:本文所提出的小波−SPWVD时频能量波长提取算法基本可行,相比于尺度−小波能量谱方法,其主要优势在于能一次算出轨道区段不平顺的时−频能量分布,时耗小(计算时间约为尺度−小波能量谱方法的1/50),且能同时表征轨道几何形变的时−频分布特征。
3 轨道病害定位方法
看起来千差万别的各种轨道不平顺波形,其实可以归纳成具有相似特性的若干类型[17]。不同的轨道病害具有不同的轨道几何波形,这为轨道病害的提取方法提供了条件。在一般情况下,每一类轨道病害均具有相似的轨道几何形变波形,因此可以从频域的角度分析不同轨道病害的频率分布特征,以病害在特征频率处的频域能量为基础,达到定位提取轨道病害的目的。
基于算法的普适性,本文主要以焊缝、凸台形不平顺为例,阐明并检算基于小波−SPWVD时−频能量分布的病害提取算法及其有效性。
3.1 基于小波−SPWVD时频能量的病害提取方法
实际上,病害提取的基本原理与波长提取原理基本相同,只是由于特征病害的波形并非常规的正余弦近似波形,呈现多样化,所以一般有多个特征频率,同时每个特征频率在病害波形中的影响系数是不一样的。因此,本文提出的病害提取方法如下:
1) 针对不同的轨道病害,统计其波形和幅值特征,提取此轨道病害的特征频率fi(i=1, 2, …, n)及不同频率对病害波形的影响系数Ci(i=1, 2, …, n);
2) 根据轨道病害的大致频率范围,确定小波重构信号,并计算其SPWVD时−频能量;
3) 根据提取的特征频率及其影响系数,从SPWVD时−频能量矩阵中获取n个特征频率下的时域能量分布Ei(i=1, 2, …, n),则病害的时域能量分布为

4) 设定特征病害的能量阈值,大于能量阈值的时域能量点即为特征病害的出现位置(与波长提取算法类似)。
3.2 算法验证
3.2.1 焊缝不平顺验证
参照文献[18]中的方法模拟焊缝不平顺的特征波形,如图7(a)所示。采用尺度−小波能量谱方法提取特征病害的特征频率及影响系数,焊缝不平顺的尺度−小波能量谱如图7(b)所示。其中,特征频率采用尺度−小波能量谱的峰值频率;影响系数Ci采用特征频率处小波能量谱值的归一化形式,如图7(c)所示。
由图7可获得此焊缝不平顺的4个特征频率及相应的影响系数。将2个焊缝不平顺内嵌至轨道不平顺波形中,内嵌焊缝波形的轨道不平顺序列如图8所示。采用上述算法对离散小波变换第2阶细节重构信号进行焊缝不平顺的定位提取,结果如图9所示。

图7 焊缝不平顺的波形特征提取Fig. 7 Extraction of waveform features of weld irregularity

图8 内嵌焊缝波形的轨道不平顺序列Fig. 8 Track irregularity series embeded with weld irregularities

图9 焊缝不平顺提取结果Fig. 9 Extraction results towards weld irregularities
由图8~9可知:焊缝不平顺波形的内嵌位置与能量峰值位置十分一致,并且定位提取的精度较高,验证了算法的正确性。
3.2.2 凸台形不平顺验证
道口、涵洞、小跨度桥、桥台过渡区常呈现凸台形不平顺,可采用下式描述[17]
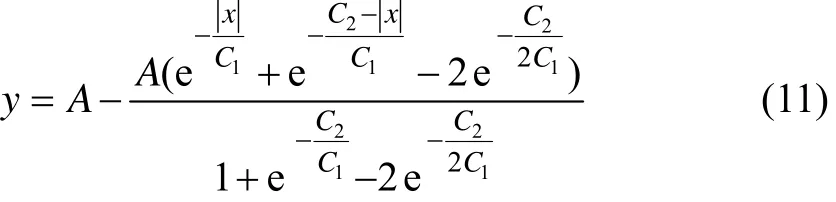
式中:取C1=0.05;C2=5;A为不平顺的幅值,A=0.1 mm。
与焊缝不平顺的处理方式一致,其波形、频谱及特征频率归一化影响系数如图10所示。
根据图 10计算所得的凸台形不平顺波形特征与焊缝不平顺的处理方法类似,将2个凸台形不平顺内嵌至轨道不平顺序列中,如图11所示。采用病害提取算法对离散小波变换第4阶细节重构信号进行频域的能量密度分布计算,如图12所示。
由图12可知:主要存在3个能量密度峰值,前2个对应的便是凸台形不平顺的内嵌位置,而第3个能量密度峰值在里程点178 m附近,此处波形特征在一定程度上也符合凸台不平顺波形特征(见图11)。

图10 凸台形不平顺的波形特征提取Fig. 10 Abstraction of waveform features of boss irregularity

图11 内嵌凸台波形的轨道不平顺序列Fig. 11 Track irregularity series embeded with boss irregularities
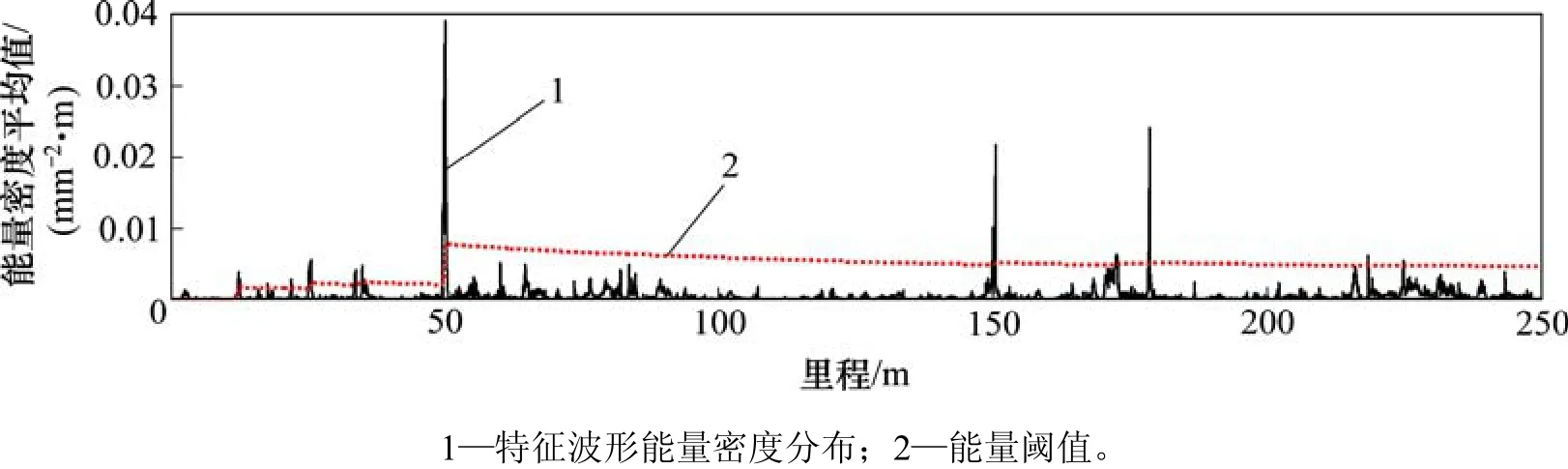
图12 凸台形不平顺的提取Fig. 12 Abstracting results towards boss irregularities
由上述2个分析实例可知本文提出的轨道病害提取算法具有较为普遍的适用性和有效性。但有3点需要注意:
1) 不同的轨道特征病害,其主要的频率能量特性是不同的,而离散小波变换是一种将原始信号序列分解到不同频段的时频处理算法,所以,对于不同的轨道病害,应该选取最为合适的小波重构信号。在具体工程应用时,可提前进行数值模拟计算,确定小波重构信号的最优阶数。
2) 本研究的轨道不平顺虽然来自于轨道综合检测车,但由于轨检车的采样精度十分有限(4点/m),如果按照轨检车的采样率进行这些特征病害波形的计算,那么将得不到完整、清晰的特征病害波形,故本文加大了采样率,相应的原始轨道不平顺序列采用“三次样条”插值方法变为同样的采样率。对于一些微小病害,由于轨检车精度有限,这些病害不一定能在轨道不平顺波形中体现出来,所以,以轨检数据为分析样本时,此病害提取算法不一定有效。但本文在轨道病害的定位提取问题中提出的算法和思想有广泛适用性,此方法的本质在于提取信号的频域能量特征,即只要获得信号在频域的基本特性,采用此算法就可以有效定位信号位置。
3) 关于能量阈值的确定需要依据大量实测数据的计算分析,本文采用小概率事件的方法只能起到近似提取阈值的作用。
4 结论
1) 分别提出基于尺度−小波能量谱和小波−SPWVD时−频能量分布的轨道不平顺波长定位提取方法。这2种方法的超阈值能量分布是基本一致的,说明2种方法在波长提取的有效性及原理上是基本一致的。但从计算经济性和时−频能量分布方面考虑,推荐小波−SPWVD时−频能量分布的提取方法。
2) 证明了小波−SPWVD 时−频能量病害提取算法的正确性。在对轨道病害波形大量实测资料的统计分析基础上,提取此轨道病害的特征波形、特征频率及不同频率对病害波形的影响系数,运用小波−SPWVD病害提取算法能有效地定位提取轨道病害。
3) 由于本文算法十分依赖信号的采样精度,而轨道综合检测车的精度有限,所以,在轨道病害的检测过程中,应该逐步将轨道几何波形检测方法转化至对应的动力响应时程特征提取,建立轨道病害−动力响应特征的映射关系,依靠此算法,并结合车辆−轨道耦合动力学基本理论,建立一种更为全面的轨道病害定位提取方法。
[1] 练松良, 黄俊飞. 客货共运线路轨道不平顺不利波长的分析研究[J]. 铁道学报, 2004, 26(2): 111−115.LIAN Songliang, HUANG Junfei. Study of the detrimental wavelengths of track irregularities for railways with passenger and freight traffic[J]. Journal of the China railway Society, 2004,26(2): 111−115.
[2] 徐磊, 陈宪麦. 基于小波和Wigner-Hough变换的轨道特征不平顺联合分析[J]. 铁道学报, 2014, 36(5): 88−95.XU Lei, CHEN Xianmai. Analysis on track characteristic irregularities based on wavelet and Wigner-Hough transform[J].Journal of the China Railway Society, 2014, 36(5): 88−95.
[3] 高建敏, 翟婉明, 王开云. 高速行车条件下轨道几何不平顺波长敏感波长研究[J]. 铁道学报, 2012, 34(7): 83−88.GAO Jianmin, ZHAI Wanming, WANG Kaiyun. Study on sensitive wavelengths of track irregularities in high-speed operation[J]. Journal of the China Railway Society, 2012, 34(7):83−88.
[4] 辛涛, 高亮, 曲建军. 提速线路轨道不平顺波长的动力仿真[J]. 北京交通大学学报, 2010, 34(6): 21−25.XIN Tao, GAO Liang, QU Jianjun. Dynamic simulation study on wavelength of track irregularities in raising speed railway[J].Journal of Beijing Jiaotong University, 2010, 34(6): 21−25.
[5] 王卫东, 刘金朝, 梁志明. 综合评价车辆/轨道系统动态特性的广义能量法[J]. 中国铁道科学, 2009, 30(5): 22−27.WANG Weidong, LIU Jinzhao, LIANG Zhiming. Generalized energy index for comprehensive evaluating the dynamic characteristics of vehicle/track system[J]. China Railway Science,2009, 30(5): 22−27.
[6] 李再帏, 练松良. 基于本征模函数的轨道质量评价方法[J].同济大学学报(自然科学版), 2013, 41(2): 213−217.LI Zaiwei, LIAN Songliang. Track quality assessment method based on intrinsic mode function[J]. Journal of Tongji University(Natural Science), 2013, 41(2): 213−217.
[7] 李再帏, 练松良, 周俊磊. 基于改进EMD方法的轨道不平顺时频分析[J]. 同济大学学报(自然科学版), 2012, 40(5):702−707.LI Zaiwei, LIAN Songliang, ZHOU Junlei. Time-frequency analysis of track irregularity based on improved empirical mode decomposition method[J]. Journal of Tongji University (Natural Science), 2012, 40(5): 702−707.
[8] 宁静, 诸昌铃, 张兵. 基于EMD和Cohen核的轨道不平顺信号分析方法[J]. 振动与冲击, 2013, 32(4): 31−38.NING Jing, ZHU Changqian, ZHANG Bing. An approach for signal analysis of track irregularity based on EMD and Cohen’s kernel[J]. Journal of Vibration and Shock, 2013, 32(4): 31−38.
[9] 徐磊, 陈宪麦, 徐伟昌, 等. 基于小波和 Wigner-Ville分布的轨道不平顺特征识别[J]. 中南大学学报(自然科学版), 2013(8):3344−3350.XU Lei, CHEN Xianmai, XU Weichang, et al. Track irregularity characteristics identification based wavelet and Wigner-Ville distribution [J]. Journal of Central South University (Science and Technology), 2013(8): 3344−3350.
[10] 王文圣, 丁晶, 向红莲. 小波分析在水文学中的应用研究及展望[J]. 水科学进展, 2002, 13(4): 515−520.WANG Wensheng, DING Jing, XIANG Honglian. Application and prospect of wavelet analysis in hydrology[J]. Advances in Water Science, 2002, 13(4): 515−520.
[11] 徐磊, 陈宪麦, 徐伟昌, 等. 小波能量谱在铁路轨道检测中的应用[J]. 振动工程学报, 2014, 27(4): 605−612.XU Lei, CHEN Xianmai, XU Weichang, et al. Application of wavelet energy spectrum in railway track detection[J]. Journal of Vibration Engineering, 2014, 27(4): 605−612.
[12] WIGNER E P. On the equation correction for thermodynamic equilibrium[J]. Physical Review, 1932, 40(40): 749−759.
[13] VILLE J. Theorie et application de la notion de signal analytique[J]. Cables et Transmissions, 1948(1): 61−74.
[14] 唐向宏, 李齐良. 时频分析与小波变换[M]. 北京: 科学出版社, 2008: 81.TANG Xianghong, LI Qiliang. The time-frequency analysis and wavelet transform[M]. Beijing: Science Press, 2008: 81.
[15] 李海峰. 有碴轨道结构的变形设计及其几何状态行为理论的研究[D]. 上海: 同济大学, 2006: 12.LI Haifeng. The research on theory of ballasted track deformation design and track geometric status[D]. Shanghai:Tongji University, 2006: 12.
[16] 许玉德. 轨道不平顺预测理论及辅助决策系统的研究[D]. 北京: 北京交通大学, 2003: 12.XU Yude. The research of track irregularity prediction theory and computer aided decision-making system[D]. Beijing: Beijing Jiaotong University, 2003: 12.
[17] 罗林, 张格明, 吴旺青, 等. 轮轨系统轨道平顺状态控制[M].北京: 中国铁道出版社, 2006: 174.LUO Lin, ZHANG Geming, WU Wangqing, et al. Track irregularity state control in wheel/rail system[M]. Beijing: China Railway Science, 2006: 174.
[18] 高建敏, 翟婉明.高速铁路钢轨焊接区不平顺的动力效应及其安全限值研究[J]. 中国科学: 技术科学, 2014, 44(7): 697−707.GAO Jianmin, ZHAI Wanming. Dynamic effect and safety limits of rail weld irregularity on high-speed railways[J]. SCIENTIA SINICA Technologica, 2014, 44(7): 697−707.
Localization methods for track irregularity wavelengths and track diseases
XU Lei1, GAO Jianmin1, ZHAI Wanming1, CHEN Xianmai2
(1. Track Power State Key Laboratory, Southwest Jiaotong University, Chengdu 610031, China;2. School of Civil Engineering, Central South University, Changsha 410075, China)
The theories of time-frequency analysis and energy mutation over characteristic waveforms were used to study the positioning and extraction of track irregularity characteristic wavelengths and track diseases. Combining wavelet transform’s multi-resolution analytical characteristics and Wigner-Ville distribution’s high time-frequency energyfocusing performance, a wavelet-SPWVE time-frequency algorithm of locating and extracting track irregularity wavelength was proposed and compared with the conventional scale-wavelet energy spectrum analysis method. Based on the method of time-frequency energy analysis, a wavelet-SPWVD time-frequency algorithm, which combines statistical characteristic frequencies and their corresponding influence coefficients of track geometries, was proposed to locate the detrimental waveforms. The results show that both the time-frequency energy analysis method and the conventional scale-wavelet energy spectrum analysis method demonstrate consistency and efficiency at aspects of the basic principle and the functionality in locating the characteristic signals. However, the time-frequency energy analysis method holds significant advantages in time-consuming and quantity of information. The effectiveness of the method is verified by examples of track diseases, i.e., the weld-type and convex-type profile.
track irregularity; wavelet transform; Wigner-Ville distribution; characteristic wavelengths; track diseases
U213.2
A
1672−7207(2017)11−3060−09
10.11817/j.issn.1672-7207.2017.11.029
2016−12−11;
2017−01−15
国家重点基础研究发展计划(973计划)项目(2013CB036205);中国铁路总公司科技研究计划项目(2014G001-G );中央高校基本科研业务费专项资金资助项目(2682015CX045);牵引动力国家重点实验室自主研究项目(2014TPL_T01);国家自然科学基金资助项目(U1234209,51478482);武汉铁路局科技发展计划资助项目(13G04,14G06) (Project(2013CB036205) supported by the National Basic Research Program (973 Program) of China; Project(2014G001-G) supported by the Scientific and Technological Research and Development Project of China Railway Corporation; Project(2682015CX045) supported by the Fundamental Funds for the Central Universities;Projects(U1234209, 51478482) supported by the National Natural Science Foundation of China; Projects(13G04, 14G06) supported by the Scientific and Technologic Development Plan of Wuhan Railway Bureau)
高建敏,博士,副研究员,从事车辆-轨道耦合动力学、线路谱等研究;E-mail: Jmgao@home.swjtu.edu.cn
(编辑 伍锦花)
