基于PIDNN的六旋翼无人机飞行控制算法研究*

徐会丽， 石明全， 张 霞， 王晓东， 井光辉

(中国科学院大学 中国科学院 重庆绿色智能技术研究院，重庆 400714)

基于PIDNN的六旋翼无人机飞行控制算法研究*

徐会丽， 石明全， 张 霞， 王晓东， 井光辉

(中国科学院大学中国科学院重庆绿色智能技术研究院，重庆400714)

针对六旋翼无人机比例—积分—微分(PID)控制器参数优化困难的问题，采用了PID神经网络(PIDNN)控制方法，利用其非线性映射和自学习的特性，实现了姿态控制参数的动态调整，增加了系统的自适应性。为验证方法的有效性，通过Matlab的Simulink模块构建了六旋翼无人机数学模型;利用S函数实现了基于反向传播(BP)算法的PIDNN控制器；将仿真结果与传统PID控制效果进行对比，结果表明：在缩短姿态调整时间与减少超调量方面，PIDNN方法控制效果优于PID方法。

六旋翼无人机； 比例—积分—微分神经网络算法； 姿态控制

0 引 言

目前，无人机研究大多数以四旋翼无人机为对象，但与四旋翼相比，六旋翼无人机在机体空间利用、负载能力等方面更具优势。另外，传统的比例—积分—微分(proportion integration differentiation,PID)方法，虽然原理简单，但用于多旋翼飞行器时，存在不易在线调参、自适应性差等问题[1]，对控制效果产生影响。

PID神经网络(PID neural network,PIDNN)控制是针对上述问题提出的一种控制策略，可用于解决非线性系统的在线控制问题[2,3]。白国振、俞洁皓[4]提出了采用基于Mamdani模型的模糊神经网络，但五层Mamdani网络结构延长了训练时间，增加了网络复杂度。陈宇峰[5]、盛贤君等人[6]提出了在输出层得到参数优化量Δkp，Δki，Δkd后再用于PID控制器，但存在输入/输出变量过多、实现难度大等缺点。鉴于以上各类型方法的不足，本文采用了将反向传播NN(back propagation NN,BPNN)与PID融为一体的控制策略，即PIDNN控制方法。该方法不再显式调用PID方法，而是将神经网络隐含层设置为比例神经元、积分神经元及微分神经元，每次迭代均对连接权重进行整定，增加了自适应性[7]。该方法控制方案清晰且能够将神经网络与常规PID控制理论的优势结合，提高了控制可靠性。

1 六旋翼飞行器数学模型建立

参照文献[8～11]建立六旋翼无人机的线运动模型和角运动模型，如图1所示。其中，1#，3#，5#电机顺时针转动，2#，4#，6#电机逆时针转动，Pitch(θ),Roll(φ),Yaw(ψ)为俯仰角、横滚角、航偏角。本文仅考虑飞行速度较小的情况，忽略空气阻力[12]，根据牛顿运动定律及大地坐标系与机身坐标系之间的转换方程，六旋翼无人机的线性运动模型为

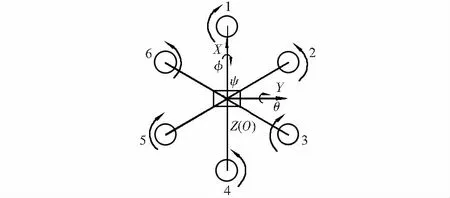
图1 六旋翼飞行器结构

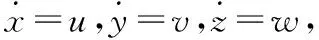
(1)

(2)

式中x,y,z为质心相对大地坐标系的位置;u,v,w为运动线速度;Ti为第i螺旋桨产生的升力;b为转速与升力的转化系数;Ωi(i=1,2…,6)为各旋翼转速。由式(1)、式(2)可得到六旋翼线加速度与控制量、姿态角的关系。

在横滚角、俯仰角较小(可忽略机身坐标和大地坐标之间的转化)情况下，通过分析飞行器所受力矩与刚体动力学方程中力矩和转动惯量的关系，可得到六旋翼无人机角运动模型

(3)

式中Jr为旋翼转动惯量;Ix,Iy,Iz为绕机身坐标系x,y,z轴的转动惯量;U1,U2,U3,U4为油门、横滚角、俯仰角、航偏角的输入值;L为螺旋桨中心到机身质心的距离。由式(3)可得到六旋翼角加速度与控制量、螺旋桨转速以及当前角速度之间的关系。

2 PIDNN控制器结构和算法

由式(1)～式(3)可知，六旋翼飞行器的角运动和其线运行情况无关。因此，可将飞行器3个欧拉角作为状态值，U1～U4作为控制器输出的控制量。

PIDNN基本结构由3部分构成：输入层、隐含层和输出层。系统结构如图2所示。神经网络输入值为欧拉角反馈值和控制目标值，输出值为控制量。

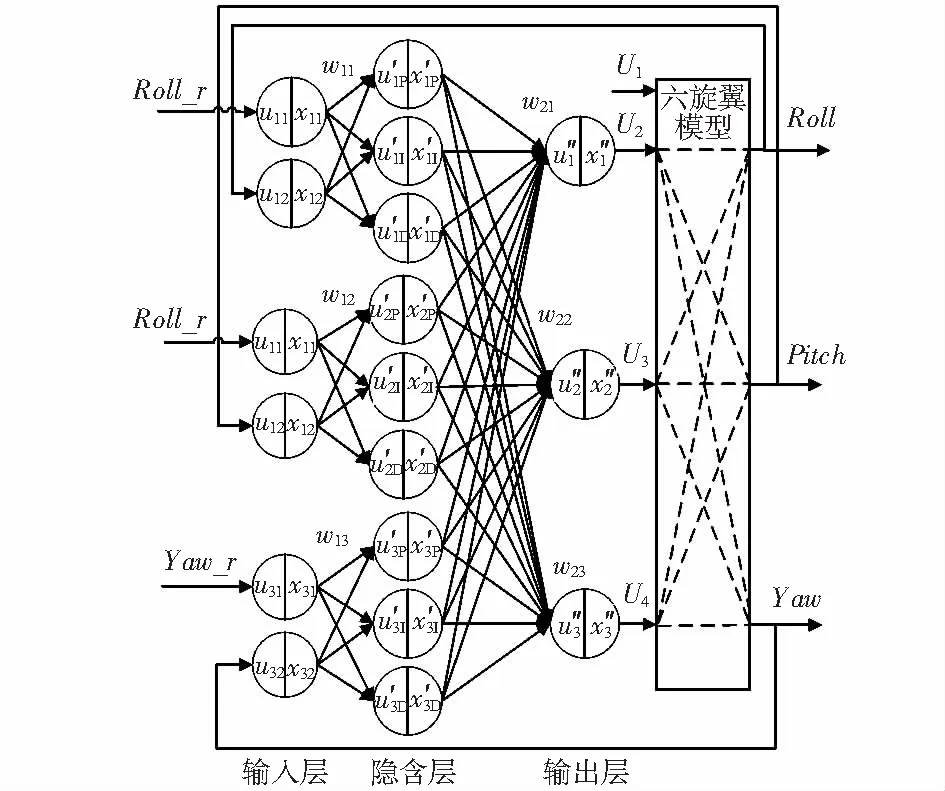
图2 控制系统结构

各子网i的隐含层为PIDNN主要构成部分，含有3种神经元:比例神经元(P)、积分神经元(I)和微分神经元(D)。比例神经元的输入输出值关系为

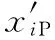
(4)

积分神经元的输入输出值关系为

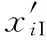
(5)

微分神经元的输入输出值关系为

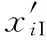
(6)

PIDNN每次迭代结束，利用梯度下降法对隐含层到输出层的连接权重更新。

另外，输入层至隐含层模拟的是误差的计算，可直接将子网的权重设定为w1i=[1 -1;1 -1;1 -1]，i=1,2,3。隐含层到输出层的权值更新公式为

(7)

(8)

式中J为3个误差平方和;ym(k)为3个欧拉角;rm(k)为设定值;η为学习速率;Em为欧拉角误差；m为输出量个数；j为输出神经元个数；uj为角度控制量。

3 PIDNN对机控制效果验证

实验为定点悬停状态下实现对飞行器姿态的控制，控制对象为3个欧拉角。仿真实验相关参数设置为：m=0.5 kg；gn=9.8 N/kg；L= 0.2 m；转动惯量Ix=0.114 kg·m2，Iz=0.158 kg·m2；b=4.5。图3为系统控制框图，其中，姿态角控制模块根据式(4)～式(8)设计完成，通过S函数实现；控制分配模型、机身刚体模型根据式(1)～式(3)建立，通过改变6个电机转速控制飞行器姿态。

首先利用传统PID控制参数调整的方式获得参数值，并将其设置为隐含层到输出层的权重。初始权重设置为w21=[2 000,800,4 000,0,0,0,0,0,0]，w22=[800,400,4 000,0,0,0,0,0,0]，w23=[2 000,800,4 000,0,0,0,0,0,0]。将输入量设为阶跃信号，训练次数设为50，对比传统PID和该PIDNN对六旋翼模型的控制效果，如图4所示。

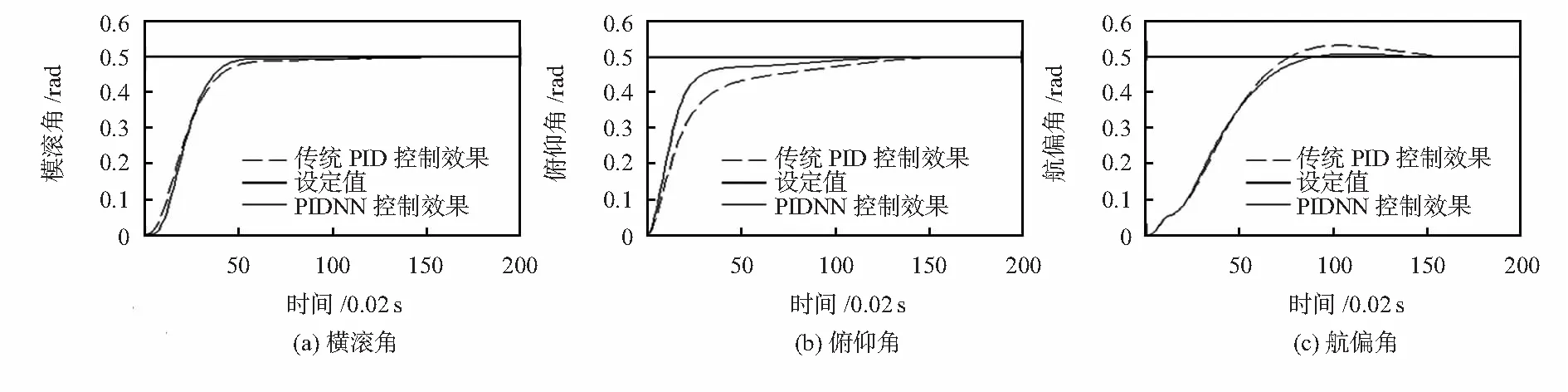
图4 传统PID和PIDNN控制效果对比

可以看出，3个欧拉角之间相互影响较小，能够按照各自的设定值调整，具体调节时间与超调量如表1。

表1 实验结果对比

由表1可以看出，横滚角调节时间缩短了1.48 s，俯仰角调节时间缩短了0.34 s，航偏角调节时间缩短了0.56 s，达到设定值的时间均得到了缩短；航偏角超调量减少了0.024 rad。可以看出，PIDNN通过BP神经网络的自学习能力可有效地根据系统反馈调整控制参数，提高收敛速度，减少姿态调整时间，并减小超调值。

4 结 论

本文主要研究六旋翼飞行器控制参数调整的动态性与姿态控制的有效性。将传统PID方法融入神经网络结构，利用BPNN的误差反向传递机制实现根据对象状态实时调整参数的目的，实现了控制器的动态在线调整。同时，仿真结果表明：方法加快了六旋翼对象到指定状态的速度，验证了方法的有效性。

[1] Mohammadi M,Shahri A M.Adaptive nonlinear stabilization control for a quadrotor UAV:Theory，simulation and experimenta-tion[J].Journal of Intelligent and Robotic Systems，2013，71(1):1-18.

[2] Chen Y，He Y，Zhou M.Decentralized PID neural network control for a quadrotor helicopter subjected to wind disturbance[J].Journal of Central South University，2015，22(1):168-179.

[3] Luo X，Si J.Stability of direct heuristic dynamic programming for nonlinear tracking control using PID neural network[C]∥The 2013 International Joint Conference on Neural Networks(IJCNN)，Dallas，Texas，USA:IEEE，2013:1-7.

[4] 白国振，俞洁皓.基于改进模糊神经网络的PID参数自整定[J].计算机应用研究，2016，33(11):1-9.

[5] 陈宇峰，蔡 琴.基于BP神经网络的PID控制参数整定[J].成都电子机械高等专科学校学报，2007(3):15-17,65.

[6] 盛贤君，姜 涛，王 杰，等.基于BP神经网络的速度前馈PID控制器设计[J].计算机应用，2015，25(S2):134-137.

[7] 杨 鹏，邢钰姣，孙 昊，等.基于BP神经网络的正四面体阵列声源定向研究[J].传感器与微系统，2012，31(5):8-9，12.

[8] 陆兴华.姿态融合滤波的无人机抗干扰控制算法[J].传感器与微系统，2016，35(7):116-119.

[9] 王 伟，邱启明.六旋翼飞行器建模及位置跟踪控制[J].电子器件，2014，37(3):507-513.

[10] Cook M V．Flight dynamics principles[M].Oxford:Elsevier Ltd，2007:66-73.

[11] 李 俊，李运堂.四旋翼飞行器的动力学建模及PID控制[J].辽宁工程技术大学学报:自然科学版，2012，31(1):114-117.

[12] Hoffmann G M，Huang H，Waslander S L，et al.Quadrotor helicopter flight dynamics and control:Theory and experiment[C]∥Proceedings of the AIAA Guidance，Navigation,and Control Conference，Hilton Head，South Carolina:AIAA，2007:4.

Researchonflightcontrolalgorithmforsix-rotorunmannedhelicopterbasedonPIDNN*

XU Hui-li, SHI Ming-quan， ZHANG Xia， WANG Xiao-dong， JING Guang-hui

(UniversityofChineseAcademyofSciences,ChongqingInstituteofGreenandIntelligentTechnology,ChineseAcademyofSciences,Chongqing400714,China)

Aiming at problem that parameters of six-rotor unmanned helicopter proportion integration differentiation(PID) controller are difficult to be optimized,a PID neural network(PIDNN)method which has characteristics of nonlinear mapping and self-learning,is developed and employed.It can adjust attitude control parameters dynamically and promote the self-adaptability of controller system.To prove the effectiveness of the method,the mathematical modeling for six-rotor is established by Simulink module in Matlab,PIDNN controller based on back propagation(BP)algorithm is obtained by S-function.Simulation results are compared with control effects of PID,verifying that control effect of PIDNN is more valid in reducing attitude adjustment time and decreasing overshoots.

six-rotor unmanned helicopter； PID neural network(PIDNN)algorithm； control of attitude

10.13873/J.1000—9787(2017)12—0025—03

V 249.1

A

1000—9787(2017)12—0025—03

2017—01—09

基于虚拟现实技术的机械系统动力学仿真系统开发及应用项目(CSTC2012GGB60001)；重庆市北碚区应用开发计划项目(Y62Z120G10)

徐会丽(1992-)，女，硕士研究生，主要研究方向为计算机控制、神经网络控制等。石明全(1975-)，男，通讯作者，教授，博士研究生导师，主要研究领域为计算机控制、机电一体化系统设计、复杂机械系统动态仿真及优化等，E—mail：shimq@cigit.ac.cn。