多项式方程的迭代方法

高 尚，王长宝

（江苏科技大学计算机科学与工程学院，江苏 镇江 212003）

多项式方程的迭代方法

高 尚，王长宝

（江苏科技大学计算机科学与工程学院，江苏 镇江 212003）

基于韦达定理，给出了求解高次代数方程迭代方法，可同时迭代出所有实解。对其收敛性作了初步讨论。给出了实例以及MATLAB源程序.

多项式方程；韦达定理；迭代方法

0 引言

由于矩阵特征值、微分方程等许多实际问题的求解往往归结为多项式的求根问题；许多实际工程问题，如信号处理中经常遇到的滤波器和最小相位系统的设计、频谱分析、语音信号处理、信道编码与解码等都转化成多项式求根问题[1-4]。4次以下的一元多项式在17世纪之前已有了公式解,但是对于5次及以上代数方程已经没有求根公式，只能求其数值解[5-6]。尽管已经出现了一些数值计算意义下的求近似解的方法，如二分法、弦截法、迭代法、牛顿法等，但是这些方法却都有模糊的先决条件和其他一些局限性。因此多项式的求根问题一直受到科技界的广泛研究，对其研究有深远地意义。一般地，我们把关于x的代数方程称 为x的n次多项式方程一般式。多项式方程基本定理：关于x的复系数方程 a xn+ a xn-1+ … + ax +a =0nn-11 0有且只有n个根（重根按重数计算）。本文基于韦达定理，拟采用迭代方法来求解2次以上的多项式方程。并且对于迭代方法一般迭代出一个根[7-10]，而本文方法将同时迭代出所有根。

1 韦达定理

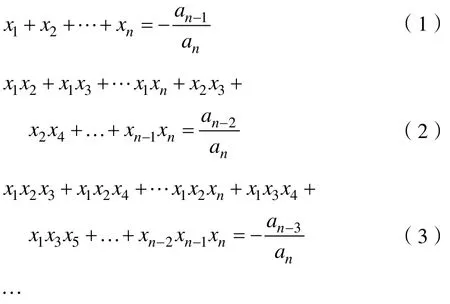
2 一元2次方程的迭代方法

3 一元n次方程的迭代方法

4 代数方程的迭代方法的收敛性

从线性方程组的雅可比迭代方法、高斯赛德尔迭代方法的收敛性可知，不是所有迭代公式收敛，须满足一些收敛条件[1-2]。对于本文的迭代方法，很明显迭代方程是非线性的，其收敛性情况更复杂。这里仅讨论一元2次方程的迭代收敛性。

先讨论改进方法的收敛性：

由公式（6）可知：

5 结束语

对于代数方程求根一般迭代方法，每次迭代只能求出一个根。而本文方法是n个根同时迭代，可得到n个根，而且方法简单，便于编程。本文只对一元2次方程迭代方法的收敛性进行了讨论，其他情况的收敛性比较复杂，还需进一步研究。

附注1 3次方程的源程序：

clear all

b=–2;

c=–1;

d=2;

e=0.00005;

x1(1)=–0.5;

x2(1)=3;

x3(1)=–d/(x1(1)*x2(1));

x1(2)=–b–x2(1)–x3(1);

x2(2)=(c–x1(1)*x3(1))/(x1(1)+x3(1));

x3(2)=–d/(x1(1)*x2(1));

i=2;

while abs(x1(i)–x1(i–1))>e || abs(x2(i)–x2(i–1))>e || abs(x3(i)–x3(i–1))>e

i=i+1;

x1(i)=–b–x2(i–1)–x3(i–1);

x2(i)=(c–x1(i–1)*x3(i–1))/(x1(i–1)+x3(i–1));

x3(i)=–d/(x1(i–1)*x2(i–1));

end

x1

x2

x3

[1] 张雅静, 田玉, 尚随明. 旋转极小曲面中微分方程通解的解法[J]. 软件, 2016, 37(02): 08-10.

[2] 刘成军. 基于消息传递接口的线性方程组并行计算研究[J].软件, 2013, 34(1): 119-120.

[3] 周振华, 赖生建. 静场Poisson方程的CUDA并行计算[J].新型工业化, 2011, 1(5): 52-58.

[4] 曾维理, 路小波. 带有非局部全变分正则项的鲁棒偏微分方程超分辨率方法[J]. 新型工业化, 2011, 1(8): 64-69.

[5] 高尚, 别小川, 秦斌. 计算方法[M]. 西安电子科技大学出版社, 2009.

[6] R. L. Burden, J. D. Faires. Numerical Analysis[M]. Higher Education Press & Thomson Learning, Inc. , 2001.

[7] 朱梅阶, 朱伟雄. 切比雪夫迭代用于多项求根及其收敛性[J]. 浙江大学学报(理学版), 2001, 28(2): 119-124.

[8] 曹敦虔, 张明. 基于进化策略方法求多项式的根[J]. 广西科学, 2007, 14(2): 98-102.

[9] 郑一. 一元n次多项式根的展开公式及其求根算法[J]. 计算机应用与软件, 2003, 20(10): 65-67.

[10] 周智恒, 洪毅, 廖芹. 一元实系数多项式方程实根的求解问题[J]. 华南理工大学学报(自然科学版), 2002, 30(5):8-11.

Iterative Methods for Polynomial Equations

GAO Shang, WANG Chang-bao
(School of Computer Science and Engineering, Jiangsu University of Science and Technology, Zhenjiang 212003, China)

Base Vieta theorem, iterative methods for polynomial equations are proposed and all roots of polynomial equation can be found simultaneously. The convergence of methods is preliminarily discussed. Examples and MATLAB source code are given.

Polynomial equations; Vieta theorem; Iteration method

TP301.6

A

10.3969/j.issn.1003-6970.2017.11.016

本文著录格式：高尚，王长宝. 多项式方程的迭代方法[J]. 软件，2017，38（11）：82-84

高尚(1972-)，教授，研究方向：数值计算，人工智能等；王长宝(1963-)，实验室，研究方向：智能信息处理，嵌入式系统等。