循环平稳理论的发展与应用

杨秀梅

（昆明理工大学 信息工程与自动化学院，云南 昆明 650093）

循环平稳理论的发展与应用

杨秀梅

（昆明理工大学 信息工程与自动化学院，云南 昆明 650093）

随着现代信号处理技术的进步，可以更加有效的处理非线性、非平稳、非高斯信号。循环平稳理论的主要研究对象是非平稳信号。本文从循环平稳理论的概念入手，介绍了循环平稳理论在算法本身方面的研究进展，并分析了与其它算法的结合应用情况，以及在不同领域的应用情况。

循环平稳；循环谱；算法；应用

0 引言

现代信号分析与处理技术是为了更加有效的解决非线性、非平稳、非高斯信号而发展起来的。循环平稳理论的主要处理对象是非平稳信号中的一类特殊信号，如水文数据、气象数据、海洋信号和机械轴承信号等，这些信号存在某阶统计量随时间按周期或多周期规律变化的现象，统称为循环平稳信号（Cyclostationary Signal简称CS）。

与传统的信号处理方法相比，CS处理最大的不同是它引入了循环频率的概念，从而将非平稳信号转化为在一定程度上平稳的信号进行处理。根据不同阶次统计量的周期性，CS可以分为一阶循环平稳、二阶循环平稳和高阶循环平稳。循环平稳理论深刻揭示了具有循环平稳特征的信号的本质特征，奠定了CS的理论基础，为CS处理技术的发展提供了方向和动力[1]。

1 循环平稳理论的研究现状

Gardner用统一的理论框架描述了时间序列谱相关函数计算方法，提出了原始算法，在以后的十几年里，出现了一些对原始算法改进的估计算法。

关于循环谱估计的研究目前大致分三条研究主线：（1）基于循环周期图的非参数经典循环谱估计；（2）基于参数估计理论的现代循环谱估计。（3）基于Wigner-ville框架的循环谱估计[2]。

1.1 理论基础

若信号 ()x t为CS，设其周期为T，以二阶循环平稳为例，则：

可将 Rx( t,τ)展开成Fourier级数的形式：

Rx(τ, α)表示循环频率为 α = m/ T 的循环自相关函数，它是以时间延迟τ和循环频率α为变量的二元函数。根据维纳—辛钦定理，对Rx(τ, α) 在τ方向上做Fourier变换：

Sx(f,α) 为谱相关密度函数（也称循环谱密度），可以认为 Sx(f,α)和 Rx(τ, α)构成循环维纳—辛钦关系[1]。当α=0时，退化为普通的维纳—辛钦关系。

循环谱密度是与平稳信号的功率谱密度相当的一个概念。数学上，“周期相关”和“循环平稳”是一对同义词。循环谱密度函数的估计，在许多文献中也叫循环谱估计，循环谱估计的复杂性远远超过了传统的谱估计。

信号 ()x t的Wigner-Ville分布定义为：

根据循环平稳的基本理论，用时间平均代替集总平均，则信号 ()x t的循环自相关函数可以表示为：

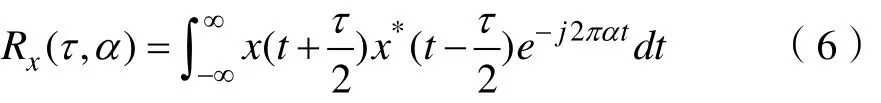
结合式（4）（5）（6），可以得到：

即对 Wx(t,f)在t方向上做 Fourier变换可得到Sx(f,α) 。

综合上面的分析，可以得到如图1的关系。当循环频率α为零时，则循环平稳信号退化为普通的平稳信号。

1.2 经典循环谱估计及其研究进展

经典循环谱估的理论依据是维纳—辛钦定理。

随着对信号循环平稳性研究的深入，许多循环谱估计算法被提出，成熟的大致有两种：分别是时域平滑算法中的 FFT累积方法（FAM，FFT Accumulation Method）和条形谱相关算法（SSCA，the Strip Spectral Correlation Algorithm），频域平滑算法（FSM，Frequency Smoothed Method）。

目前经典循环谱估计的大部分改进算法都是基于数据分段、加窗、重叠等方法或者多个方法的联合使用，通过分析改进算法在循环谱估计的方差、来评价改进算法。抑制噪声能力、循环谱的分辨率或者计算量等方面。

图1 R x (t , τ ) , R x (τ , α ), W x (t , f ), S x ( f ,α)关系图

高玉龙利用改进 FFT算法和位相关算法代替SSCA算法中滑动FFT和相关算法，并给出了改进算法的数字实现方法和步骤，基本实现了对循环谱的实时分析[3]。

翁虹将时间重叠法和 ssinc窗应用于循环谱估计中，提出了时间重叠的循环谱估计方法，使循环谱估计取得了新的进展：（1）循环谱的偏离误差减小，有效频率分辨率提高，能准确地分辨出循环频率方向和循环频率轴方向的谱峰；（2）计算量大大减少，提高了循环谱的实时性[4]。

梁红等对 FAM 算法进行了改进，在进行循环谱计算之前，先对信号进行小波变换预处理，同时在不影响到信号的循环特性的前提下，用哈特莱变换代替 FFT，改进方法降低了对信噪比的要求，并减少循环谱计算时间[5]。也有学者用Chrip-z变换代替FFT，降低了运算量、提高了分辨率。

崔伟亮等对FSM算法进行了改进，提出平均的频域平滑算法（AFSM，Averaged Frequency Smoothed Method），将加窗和叠加处理引入频域，有效降低了估计方差和数据量的要求，并从理论和实践证明了算法的有效性，AFSM 可用于低信噪比、小数据量、高分辨率要求下的循环谱估计[6]。

针对AFSM算法计算量大以及对不同长度数据算法程序不一致的问题，翟晓光从减少 DFT 运算量和减少相关运算量两方面对原算法进行了改进，在不改变原算法估计效果的前提下，减小了 AFSM算法的运算量和复杂度，使其适用于任意长度的数据[7]。张洋等提出了一种基于比特谱相关算法改进循环谱估计的快速算法，在不改变原有的AFSM的谱分辨率的情况下，将算法的复乘运算量降低一个数量级[8]。

从本质上讲循环谱估计是估计谱成分之间的相关性，大部分研究认为正是大量的相关运算而不是谱成分计算带来了循环谱估计计算的复杂性。因此这些方法多是从寻找有效的谱相关计算方法来提高循环谱估计的计算效率。但事实上，循环谱估计的有效性和质量的提高并不单纯的依赖于相关性的计算效率，谱成分估计的质量和效率也影响着其后的谱相关运算。因此，谱成分的计算效率和质量仍有很大的研究空间。

1.3 现代循环谱估计

根据参数模型法，任何信号都可以看成是激励通过一个系统后产生，而循环平稳随机信号可以用线性周期时变参数（LPTV）模型来建模。

LPTV模型，简单来说是对一平稳信号进行线性周期时变变换得到一线性非平稳周期信号，通过改变平稳信号（即基底函数）和模型参数来得到相应的循环平稳信号，其中模型的参数为时变的，具体过程的数学表达式如下[1]：

其中 模型参数h( t, u)行向量，基底函数 x ( u)为列向量。循环平稳信号的参数化方法根据信号的某些先验信息（或一些假设），建立一个近似信号模型来表征给定的信号。在建立模型后，用采样数据估计模型结构参数，从而进一步求出循环自相关函数、循环功率谱等其他统计量。

Gardner研究了循环平稳信号的LPTV滤波器，运用Gardner提出的概念，Ohno和Sakai从循环谱的定义出发提取了LPTV系统输出的循环谱。

国内有学者用LPTV模型估计信号的循环谱，从而提取信号的循环谱特征实现通信调制信号的识别。从模型的结构参数特征的差异来识别信号，运算量降低，也更直观[9]。

1.4 与其他算法的结合

（1）与小波变换的结合

一些学者将小波及小波包理论与循环平稳理论相结合，融合两种算法的优势，提高分析结果的可靠性。其基本思想是利用小波将信号进行分解重构后，再计算其谱相关密度函数，由此可以解调出信号中的所有调制频率，有效抑制噪声和干扰信号对解调结果的影响[1]。

（2）与盲源分离的结合

盲源分离的基本思想是在对传递系统未知，仅给出系统输出的情况下，对激励系统的多个独立源进行分离。一些学者将盲源分离与循环平稳理论相结合，基于盲信号分离的思想，将采集到的信号依次分解得到周期信号、循环平稳信号和剩余信号。再利用循环平稳理论对分解以后的信号进行下一步的处理。

明阳利用信号展现二阶循环平稳特性，提出了基于循环平稳的卷积混合频域盲分离方法。利用循环平稳信号谱相干特性，解决了频率盲分离排序不确定性的问题[11]。

一些盲算法中利用了信号二阶循环平稳特性，同时大部分信号的时变自相关函数含有多个不可约周期的谐波分量，如果全面的利用这些循环频率将会大大提高盲算法的性能。

（3）与自适应理论的结合

循环平稳与平稳的本质区别在于统计特征的周期时变。一些学者借鉴平稳随机过程自适应滤波的经验，将维纳--霍夫方程、最陡下降法、LMS算法等维纳滤波的基础思想推广到循环平稳层面，形成了循环维纳滤波理论，用于对循环平稳信号的自适应滤波。

（4）与EMD的结合

经验模态分解(EMD, Empirical Mode Decomposition)是近年来发展起来的一种时频分析方法，它不需要先验的基底，本征模函数是基于序列数据自适应得到的，该方法得到的Hilbert谱具有比较明确的物理意义，可以很好地表明信号在某一瞬时的频率组成及各频率的幅值[1]。

目前与EMD的结合，主要集中在将EMD分解作为循环谱分析的前处理。有学者用 EMD方法将信号中不同尺度的波动或趋势逐级分解，产生一系列具有不同尺度的数据序列，每一个序列为一个固有模态函数（IMF）。EMD分解后进行IMF时间尺度滤波来有效抑制噪声，提高了在循环谱截面上进行载频和码元速率估计的性能，为QPSK信号的参数估计提供了一条有效的解决途径。

全海燕等用 EMD将重力固体潮信号分解得到IMF，再利用循环相关谱描述信号频谱之间的调制关系，成功解调出重力固体潮信号中的半日波分量、日波分量和半月波分量，并得到了个分量之间的乘性调制关系[12]。

马增强等将 EMD和循环平稳分析应用于滚动轴承故障信号，用EMD分解得到故障信号的IMF，再利用循环谱分析识别故障类型[13]。

（5）与高阶累积量的结合

高阶累积量受噪声影响较小，具有较好的抗干扰性，但是无法完全识别通信系统所采用的调制方式，利用高阶累积量特征参数与循环谱特征相结合的混合识别算法可实现数字调制信号的分类[14]。

文献[15]结合了高阶累积量和循环谱算法的优点，计算Wifi信号和LTE信号的循环谱后，截取循环谱的α平面，在α平面上计算累积量 C41，作为特征向量来识别Wifi信号和LTE信号。联合算法可以很好地识别出常见的无线通信信号，具有很高的识别效率和精度，为后续频谱的优化奠定了基础。

（6）与压缩感知的结合

针对传统的循环谱计算量大的问题，韩小石等将压缩感知技术与循环谱估计结合起来，利用信号频谱和循环频谱两个维度的稀疏特性来完成循环谱的估计，在保证循环谱估计精度的条件下，降低了处理数据量和处理时间[16]。

2 循环平稳理论的应用

2.1 通信信号

通信信号被加载了各种调制信息，并且传输过程会引入很多噪声。循环平稳理论在通信信号处理上的应用主要表现在信号的检测和调制识别方面，例如信号的功率检测，MPSK信号码元速率估计，OFDM信号循环谱结构分析等。

闵泉云将循环平稳理论应用于深空通信信号检测。利用信号循环谱的全部信息，检测性能得到明显提高，仿真结果表明对多普勒频移具有很好的鲁棒性，对深空通信条件下的信号检测有一定的适用性。

刘欢对通信信号处理时，将循环平稳理论引入其中，对信号进行循环谱分析，并利用LPTV模型来分析数字通信调制信号的特性，提取数字通信调制信号循环谱的相关特征用于调制识别[9]。

文献[17]在理论上推导了无线光副载波调制QPSK信号的循环自相关函数的数学表达式，并对实测信号的循环谱和循环自相关函数进行了分析，证明有限强度的大气湍流并未破坏QPSK信号的循环平稳特性。

文献[18]将循环谱应用于 BPSK信号角跟踪。利用BPSK信号在全相干循环频率处的谱相关特性,提出循环谱峰值法，仿真结果表明该方法在较低信噪比且含有和差通道相关噪声的条件下仍能具有较高的角误差值估计精度。

郭祥宸等对SNCK调制信号的循环谱截面进行了仿真，得到了载波频率和码元速率两种特征参数。翟晓光等将循环平稳理论应用于窄带通信信号时延的估计；李冬霞等在理论上推导出载波偏置 DME信号的循环自相关函数和循环谱的表达式，并仿真验证了的循环平稳特性。

2.2 机械振动信号

旋转机械滚动轴承振动信号具有明显的周期时变特征，它是国内外应用循环平稳最多和较早的领域。大多学者采用二阶循环统计量进行信号分析，做基于循环频率---频率二维表示的特征提取技术，有效提取噪声干扰下的早期微弱故障特征。

由于循环谱一次切片对故障特征的表示不清晰和直接，周宇对特定循环频率α对应的循环双谱一次切片做进一步的切片，使其成为一个清晰的二维图谱。最后得到的二维图谱为一个循环双谱的二次切片。

针对机械领域参考信号难以获得的问题，明阳分析了旋转机械的循环平稳机理，给出了滚动轴承点蚀故障信号模型，经过数学推导得到滚动轴承各类型点蚀故障的二阶循环平稳特性[11]。

罗宏林将循环平稳理论的应用从实信号扩展到复信号，定义了二阶定向循环统计量，证明了定向循环自相关函数不仅能够表示复信号的正反进动分量在平面内的时间－ 循环频率分布信息，还能指示在指定循环频率处的旋进方向。

黎敏在利用循环谱分析滚动轴承故障信号时将信息熵与循环平稳理论结合，利用每个循环频率切片的熵值大小衡量该循环频率的信息量，以此作为每个循环频率的权重，弱化干扰频率的影响。

2.3 水声信号

水声信号以及舰船辐射噪声是典型的非平稳信号。基于循环平稳信号分析的基本理论，李长柏提出了舰船辅机工作频率与推进系统工作频率的循环频率谱特征分析方法，提取了三类舰船辅机工作频率的特征和推进系统工作频率的特征。

葛君山以三阶循环谱对机械噪声、螺旋桨噪声和水动力噪声进行分析，先计算其3阶循环谱，然后对3 阶循环谱进行切片分析，能够有效的对海面噪声进行特征分析。

2.4 生物医学信号

大部分的生物电信号，例如脑电波、心电波及肌肉电等信号都属于准周期非平稳信号，用循环平稳理论进行分析，更能揭示信号的本质特征。

李婷提出了一种基于循环平稳包络的心音分自动把第一心音和第二心音从每个周期中分别提取出来，分割的正确率超过96%。

张爱华将循环平稳信号理论应用于脉搏信号的处理，用SSCA算法得到循环频率，利用循环频率计算脉搏信号的质量系数，根据质量系数来剔除采集质量差的数据，再利用循环相关匹配滤波来进行降噪处理。

3 结论

利用信号循环谱实现信号检测首先遇到的第一个问题就是复杂度较高，虽然已有很多学者就快速实现循环谱进行了研究，单复杂度依然比较高，在实时处理要求较高的环境中仍然较难满足要求。

在大部分的循环谱应用和研究中，主要使用的是低阶（一阶和二阶）循环统计量。高阶循环统计量应用在工程实际分析与研究中仅仅是最近几年的事情。高阶循环统计量对高斯噪声和非高斯噪声都具有自动免疫性能。但是高阶循环统计量的分析需要更长的数据，其计算方法也更加复杂。

对于循环谱估计理论的研究，主要是基于经典谱估计的算法来展开，在参数谱估计方面的研究文献较少，进展比较缓慢。根据传统的平稳信号的谱估计研究理论，参数谱估计将能比经典谱估计能获得更高的分辨率和更好的性能。

目前与循环平稳理论相结合的处理方法实际上都是级联处理，也就是利用循环相关或谱相关分离所需信号和干扰信号，或者利用其它算法（如小波、EMD）先将待处理信号进行某种分解，再利用循环平稳理论做进一步的分析。

彭畅通过分析定向 Wigner分布与定向循环统计量之间的内在联系，揭示了定向Wigner分布实质上属于二阶定向循环统计量。利用谱相关密度函数的 Wigner-Ville分布可以极大削弱噪声对时频图的干扰，并且有很好的时频聚集性。

对循环平稳理论本质的深入研究，分析与其它算法的内在联系，将可以完善整个现代信号处理的理论体系，让深藏在复杂信号内部的简单奥秘得以揭示。

[1] 陈进, 董广明. 机械故障特征提取的循环平稳理论及方法[M]. 上海交通大学出版社, 2013.

[2] 何继爱, 裴承全, 浦阳阳. 信号分析与处理的方法研究[J].无线通信技术, 2012(2): 12-15.

[3] 高玉龙, 张中兆. SSCA算法改进及实现[J]. 哈尔滨工业大学学报, 2008(9): 1374-1377.

[4] 翁虹, 王宏远, 余国文. 时间重叠的循环谱估计[J]. 微电子学和计算机, 2007(9): 39-41.

[5] 梁红, 彭超, 魏晓磊. 低信噪比下信号循环谱的实现[J].通信对抗, Vol. 35, No. 2, 2016(6): 9-12.

[6] 崔伟亮, 江桦, 李剑强, 等. 改进的循环谱估计快速算法与性能分析[J]. 电子与信息报, Vo1.33 No.7, 2011(7):1594-1599.

[7] 翟晓光, 武传华. 改进的任意长度循环谱估计快速算法[J].电子信息对抗技术, Vo1.31 No.2, 2016(2): P33-39.

[8] 张洋, 彭华. 比特谱相关改进循环谱的单通道混合信号参数估计快速算法[J]. 信号处理, Vol. 32, No.4, 2016 (4):404-416.

[9] 刘欢. 基于循环平稳理论的数字调制信号识别研究[D].兰州理工大学, 2014.

[10] 宋晓瑞, 郑海昕, 况学伟. 基于循环谱特性的BPSK信号角跟踪方法研究[J]. 通信技术, Vol.49, No.7, 2016(7):842-847.

[11] 明阳. 基于循环平稳和盲源分离的滚动轴承故障特征提取方法研究[D]. 上海交通大学, 2013.

[12] 全海燕, 刘艳. EMD模态分量的谱相关分析法及其对重力固体潮信号的解调分析[J]. 地球科学进展, Vo1.31, No.9,2016(9): 919-925.

[13] 马增强, 谷朝健, 柳晓云. 多通道相关－经验模式分解在滚动轴承故障诊断中的应用[J]. 石家庄铁道大学学报(自然科学版) Vol.30, No.1, 2017(3): 64-69.

[14] 赵雄文, 郭春霞, 李景春. 基于高阶累积量和循环谱的信号调制方式混合识别算法[J]. Vol.38, No.3, 2016(3):674-680.

[15] 龙晓红, 张洪欣. 基于高阶累积量和循环谱算法的常用无线通信信号盲识别技术[J]. 滨州学院学报, Vol.32, No.2,2016(4): 59-63.

[16] 韩小石. 一种基于稀疏特性的循环谱估计方法研究[J]. 信息通信, Sum No.161, 2016 (5): 13-15.

[17] 解孟其, 柯熙政. 无线光副载波信号的循环谱分析[J]. 光学学报, Vol. 35, No. 2, 2015(2): 1-7.

[18] 翟晓光, 武传华. 窄带通信信号时延估计的循环谱组合切片法[J]. 舰船电子对抗, Vol.39 No.2, 2016: 26-30.

[19] 罗宏林, 刘小峰. 柏林滑动轴承油膜失稳振动的二阶定向循环平稳性分析[J]. Vol.35, No. 2016(4): 49-55.

[20] 彭畅. 旋转机械轴承振动信号分析方法研究[D]. 重庆大学, 2014.

[21] 何继爱, 裴承全, 蒲阳阳. 非高斯模型下BPSK的循环普分析[J]. 兰州大学学报(自然科学版), Vol.48, No.3, 2012(6):133-138.

[22] 郑鹏, 张鑫等. SCCA算法改进及性能分析[J]. 电子设计工程, Vol.19, No.17, 2001(9): 105-108.

[23] 刘佳. 单通道盲源分离及其在水声信号处理中的应用研究[D]. 哈尔滨工程大学, 2011(4): 10-12.

[24] 张各各, 王俊, 吴日恒. 复杂环境下的循环平稳信号DOA估计[J]. 西安电子科技大学学报(自然科学版), Vol.42 No.1, 2015(2): 91-97.

[25] 马国宁. 高效循环谱估计算法的研究及其应用[D]. 电子科技大学, 2006.

[26] 刘乐, 陈瑾. 基于OFDM频域内插导频的循环平稳特征频谱感知方法研究[J]. 现代导航, Vol 1, 2015(2): 65-70.

[27] 苏挺, 基于多通道最大熵谱估计的直接序列扩频信号的循环谱检测方法[D], 西安电子科技大学, 2008(1): 17-35.

[28] 燕展, 钟子发等, 基于改进循环谱的DVB_S2信号符号速率估计算法[J], 火力与指挥控制, Vol.39, No.3 2014(3):15-19.

[29] 李长柏, 基于高阶谱和循环谱的舰船噪声多源特征分离研究[D], 西北工业大学, 2005(3): 43-62.

[30] 汪赵华, 陈昊等, 基于频域平滑循环周期图法的直接序列扩频信号的参数估计[J], 中国科学技术大学学报, Vol.40,No.5, 2010(5): 466-473.

[31] 李婷, 唐洪, 基于循环平稳包络的心音分割方法, 大连民族学院学报[J], Vol.16, No.5, 2014(9): 552-554.

[32] 刘婷, 基于循环平稳分析的雷达辐射源特征提取与融合识别[D], 西安电子科技大学, 2009(1): 22-32.

[33] 邓正宏, 徐继伟等, 基于循环平稳检测算法SSCA的FFT模块设计[J], 西北工业大学学报, Vol.31 No.5, 2013(1):706-709.

[34] 周宇, 基于循环平稳信号二维平面表示的滚动轴承早期故障诊断方法研究[D], 上海交通大学, 2012(10).

[35] 高玉龙, 基于循环谱的调制方式识别与高动态同步技术研究[D], 哈尔滨工业大学, 2007(3): 28-61.

[36] 闵泉云, 基于循环谱相关的深空通信信号检测[D], 西安电子科技大学, 2013(3): 47-61.

[37] 何呈，胡新欢等，基于循环谱与模式识别的并扩信号检测[J],哈尔滨商业大学学报、(自然科学版)，Vol.28 No.6,2012(12): 678-681.

[38] 张伟涛, 刘宁等, 利用二阶循环平稳性的信道自适应盲辨识[J], 振动与冲击, Vol.29 No.8, 2010(8): 13-17.

[39] Jerome Antoni, Cyclic spectral analysis in practice, Mechanical Systems and Signal Processing 21 (2007): 597–630.

[40] 刘锋, 郑鹏等, 一种改进的循环谱估计算法[J], 电路与系统学报, Vol.18, No.1, 2013(2): 397-402.

[41] 肖云魁, 曹亚娟等, 用循环谱理论分析柴油机曲轴轴承加速振动信号[J], 振动、测试与诊断, Vo1.28 No.2, 2008(6):117-121.

[42] 翁虹, 准循环平稳信号谱相关估计与应用[D], 华中科技大学博士学位论文, 2006(11).

[43] Gardner W A. The spectral correlation theory of cyclostaionary time-series[J]. Signal Processing, Vo1.11, No.1,1986(1): 13-16.

[44] 黄知涛. 循环平稳信号处理及应用[M]. 北京: 科学出版社, 2006: 23-26.]

[45] 李冬霞, 李思, 刘海涛, 载波偏置测距仪信号的循环平稳特性[J], 系统工程与电子技术, Vol.3 No.8 2016(8):1935-1938.

[46] 郭祥宸, 孙志国, 正弦型非线性调频键控信号循环谱分析[J], 《自动化技术与应用》2017年第36卷第1期, p67-70.

[47] 吴昊, 茅玉龙, 曹俊纺, 基于循环谱相关的雷达信号脉内分析改进算法[J], 火力与指挥控制, Vol.41, No. 9, 2016(9):123-127.

[48] 黎敏, 阳建宏, 王晓景, 基于信息熵的循环谱分析方法及其在滚动轴承故障诊断中的应用[J], 振动工程学报,Vol.28, No.1, 201(2): 164-173.

[49] 张爱华, 胡文龙, 丑永新,基于循环平稳算法的脉搏信号质量评估与滤波[J], 中国医疗器械杂志, Vol.39, No. 2,2015(2): P83-86.

[50] 葛君山, 海面多源噪声的高阶循环频谱分析研究[J], 舰船科学技术, Vol.38, No. 3A, 2016(3): 64-66.

The Development and Application of Cyclostaionary Theoretic

YANG Xiu-mei
(Faculty of information engineering, and automation, Kunming University of Science and Technology, Kunming 650093, China)

The progress of modern signal processing can help us to process non-stationary and nonlinear signal more effectively. The subject investigated of cyclostaionary theoretic is non-stationary signal. This paper from the concept of cyclostaionary theoretic, introduced the Research progress on algorithm of cyclostaionary theoretic, analyzed the Combined with other algorithm, and the applications Different areas.

Cyclostaionary; Cyclic spectrum; Algorithm; Applications

TP 911.72

A

10.3969/j.issn.1003-6970.2017.11.007

本文著录格式：杨秀梅. 循环平稳理论的发展与应用[J]. 软件，2017，38（11）：40-45

云南省教育厅面上项目资助(KKJA201303016)

杨秀梅(1982-)，女，硕士，讲师。主要研究方向：现代信号处理。