长江经济带生态效率及收敛性分析

赵鑫，胡映雪，孙欣

长江经济带生态效率及收敛性分析

赵鑫1，胡映雪2，孙欣1

（1.安徽财经大学 统计与应用数学学院，安徽 蚌埠 233000；2.美国犹他州立大学 亨思迈商学院）

针对现有效率测度模型的缺陷，本文采用三阶段超效率DEA模型的Malmquist - Luenberger指数法，对长江经济带生态效率进行测算，同时借鉴新古典经济增长的收敛性假说，探究其收敛性。结果显示：调整后整体及上、中游生态效率增长率降低，下游几乎没有变化，说明上、中游处于较好的外界环境和运气状态；外界环境变量对生态效率的投入产出松弛变量存在显著影响，且影响方式不同，有必要进行第二阶段调整；整体及上中下游生态效率不存在σ收敛，整体及上游存在绝对β收敛，在经济发展速度、外资利用、产业结构、环境规制、能源消费结构和人力资源六种控制变量中，经济发展速度、产业结构和能源消费结构是促使其存在条件β收敛的重要因素。

长江经济带；生态效率；三阶段超效率DEA；ML指数；收敛性

一、引言

当前，资源与环境质量恶化已经成为制约中国经济持续发展的瓶颈因素。改革开放以来，我国经济发展取得的成就举世瞩目，国民生产总值由1978年的3 645.2亿元增长到2015年的109 893.1亿元（以1978年为基期计算）。与此同时，我国环境问题带来的挑战也更加严峻，如2000年到2015年，工业废水排放量从415.2亿吨上升到735.3亿吨，增长77.1%；工业废气排放量从138 145亿立方米增加至685 190亿立方米，增幅近4倍；工业固体废物产生量从8.2亿吨提升至33.1亿吨，同样大幅提升391.5%。经济的快速发展引致资源能源紧缺、生态环境失衡等问题，因此，对经济与资源环境协调可持续发展的关注日益增加。可持续发展以生态经济建设为基础，它主张人类社会通过创造有价格竞争优势的产品和服务来满足人类的需求并提高生活质量，同时将其环境影响和资源利用强度控制在地球的承载力水平之内（WBCSD，1996）。

在“新常态”的大背景下，大力推进长江经济带建设正当其时（李春艳和文传浩，2015）。从长江流域本身看，最核心的问题是生态环境，2016年1月召开的中央财经领导小组第十二次会议以及在重庆召开的推动长江经济带发展座谈会上，习近平强调，推动长江经济带发展，要坚持生态优先和绿色发展，合理统筹各项资源要素，使沿江各省市的协同作用更明显，促进长江经济带实现上中下游协同发展、东中西部互动合作，把长江经济带建设成为我国生态文明建设的先行示范带、创新驱动带、协调发展带。

二、文献综述

对于“生态效率”的概念， Schaltegger和Sturm（1990）最初以经济活动所产生的经济价值与环境污染为基础，定义生态效率即经济增长与环境影响的比值。世界经济合作与发展组织（OECD）（2004）拓宽了生态效率的概念，指出较高的生态效率意味着资源要素的投入能够带来产业附加值的最大化和环境污染最小化。随着研究的深入，更多机构和学者将目光聚集在构建生态效率评价指标体系上，德国环境经济账户中选取土地、能源、水、原材料、温室气体和酸性气体六种自然要素构建投入产出指标体系（Höh H et al， 2002）； Michelsen et al，（2006）选取9个环境指标构建出挪威家具产品的生态效率指标；李胜兰等（2014）基于地方政府竞争的视角，从资源消耗、环境污染和经济数据构建区域生态效率指标体系。

目前国际公认的进行环境绩效评价最好的方法之一是数据包络分析法（Data Envelopment Analysis，DEA）。Dyckhoff 和Allen （2001）纳入“坏”产出，系统地推导出测度企业环境管理生态效率的DEA模型； Hoang 和Alauddin（2012）基于投入导向型的DEA模型框架，对30个OECD国家的农业生态效率水平进行测度；lo Storto（2016）利用考虑非期望产出的DEA模型对116个意大利省会城市2011年的城市生态效率进行实证分析；黄建欢等（2015）从多维生态效率的视角利用超效率DEA模型测度中国省域生态效率；彭红松等（2017）利用SBM-DEA模型测度旅游地复合系统的生态效率。DEA方法在测算多投入和多产出评价对象的生态效率时具有较大优势，但以上DEA模型并没有考虑外界环境和随机误差对生态效率测度结果的影响，结果可能无法反映生态效率的真实值。

现有文献对非期望污染物进行处理时具有较大争议，通常将污染物直接作为投入指标，如邓波等（2011）。但在特定生产过程中，污染物与资源投入不可能总保持同比例关系，因此该处理方式不能反映真实的生产过程。也有学者将污染物通过一个合适的转移向量转化为正向输出量（Seiford和Zhu，2002），如华坚等（2013），该方法虽然未改变有效前沿面，但是无效率DMU因选取的模型不同会导致效率值出现差异。少数学者将非期望产出指标转为倒数后作为正向输出量，如蓝虹和穆争社（2016），该方法进行了非线性转换，这将改变DMU的有效前沿面，导致评价结果出现误差。

本文采用三阶段超效率DEA模型的Malmquist-Luenberger指数法（简称ML指数），它相比现有评价方法具有较大优势。首先，传统的DEA模型在面对多个DMU同时有效时，无法进一步区分；其次，将ML指数与DEA模型结合有效解决了纳入非期望产出的争议；最后，普通三阶段DEA模型虽然考虑到外界环境和随机误差的影响，但只能分析截面数据，难以反映效率的动态变化情况。本文模型综合了超效率DEA、ML指数以及三阶段DEA的优点，克服了以上缺陷，为评价长江经济带生态效率提供了一种崭新的视角。

三、模型方法、评价指标体系构建及变量说明

（一）三阶段超效率DEA模型的ML指数分析法

Fried et al（2002）在传统DEA模型的基础上，将其与随机前沿分析（Stochastic Frontier Analysis，SFA）方法相结合，提出三阶段DEA模型，该模型能够控制外生环境变量和随机误差的影响对效率评估所造成的偏误，其构建和运用包括三个阶段：

第一阶段：使用超效率DEA模型的ML指数法测算长江经济带11个省市的生态效率指数及投入和产出松弛值。ML指数可分解为技术效率变化（Ef fi ciency Change，EFFCH）和技术进步（Technical Change，TECH ），分解式（1）如下：

其中，TECHt,t+1指数表现环境生产前沿面在t 到t+1时期的移动，EFFCHt,t+1指数测度技术落后区域在t 到t+1时期对技术先进区域的生产可能性前沿追赶的程度。

第二阶段：利用类似SFA方法对初始的投入和产出松弛值进行分析，剥离出内部管理无效率、外部环境因素和随机误差等对效率产生的影响。设有K 个DMU，每个DMU有M 项期望产出，I 项非期望产出，N项投入。以构建期望产出松弛变量与外界环境变量的SFA模型为例，如下式（2）：

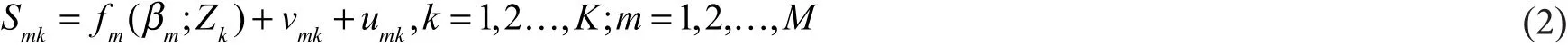
其中，Smk表示第一阶段中第k 个DMU第m 项期望产出的投入松弛值；fm(βm;Zk)表示外界环境因素对松弛值的影响，Zk=[Z1k,…,Zjk]为J 个外生环境变量，βm为环境变量的待估参数；vmk+umk为混合误差项，vmk表示随机误差影响，vmk～N(0,)，umk表示管理无效率，假设其服从零点截断正态分布umk～N+(0)，两者独立且不相关。当γm=)趋近于1时，表明内部管理无效率因素占主导地位，而当γm趋于0时，表明随机误差因素的影响占主导地位。

为同时将每个DMU的外界环境和随机误差项调整至相同状态，利用Jondrow et al（1982）提出、由罗登跃（2012）改进的方法从混合误差项ε=v+u中将随机因素分离出来（为方便起见，分离公式省略下标，该公式对投入和产出松弛变量进行分离均适用），具体分离公式如下式（3）：

式（4）反映外界环境因素和随机干扰对生态效率的影响程度，同时反映纯粹的因管理技术导致的效率低下。调整方程如下式（5）：

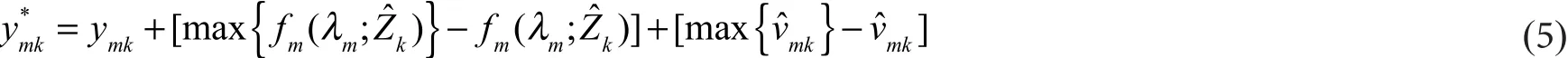
第三阶段：利用调整后的产出和投入变量数据，采用第一阶段的超效率DEA模型的ML指数法重新测得生态效率值，第三阶段得到的生态效率值剔除了外界环境因素和随机误差的影响。

（二）评价指标体系的构建

生态效率是经济、资源和环境三方面的综合反映。本文从资源消耗类、环境影响类和经济类指标构建长江经济带的生态效率评价指标体系，如表1，研究期间为2004-2015年。

（1）资源消耗类指标：选取能源、土地、水三种自然资源和劳动力、资本两种社会资源，具体为：以建设用地面积衡量土地资源投入；选取能源消费总量衡量能源投入；以全社会用水总量表征水资源投入；选取三大产业从业人员总数表征劳动力投入；在选取资本投入指标时，多数学者采用永续盘存法计算资本存量，但该方法对基期资本存量以及折旧率的选择具有较大出入（张军和章元，2003）。在过去20多年中，全社会的固定资产投资和固定资本形成数据的增长趋势基本保持一致（卢丽文等，2016），而数据包络分析方法是对相对效率进行测度，保证样本数据具有相对一致性，分析结果就不会有较大偏差。因此，本文选用全社会固定资产投资总额作为资本投入的代理变量，以2004年为基期进行缩胀处理。

（2）环境影响类指标：用全社会废水排放总量表征全社会废水排放对环境的污染；以全社会烟粉尘排放总量和全社会二氧化硫排放量来表征废气污染对环境的影响。

（3）经济类指标：选取地区GDP进行衡量，同样为剔除价格因素影响，以2004年为基年做了缩胀处理。

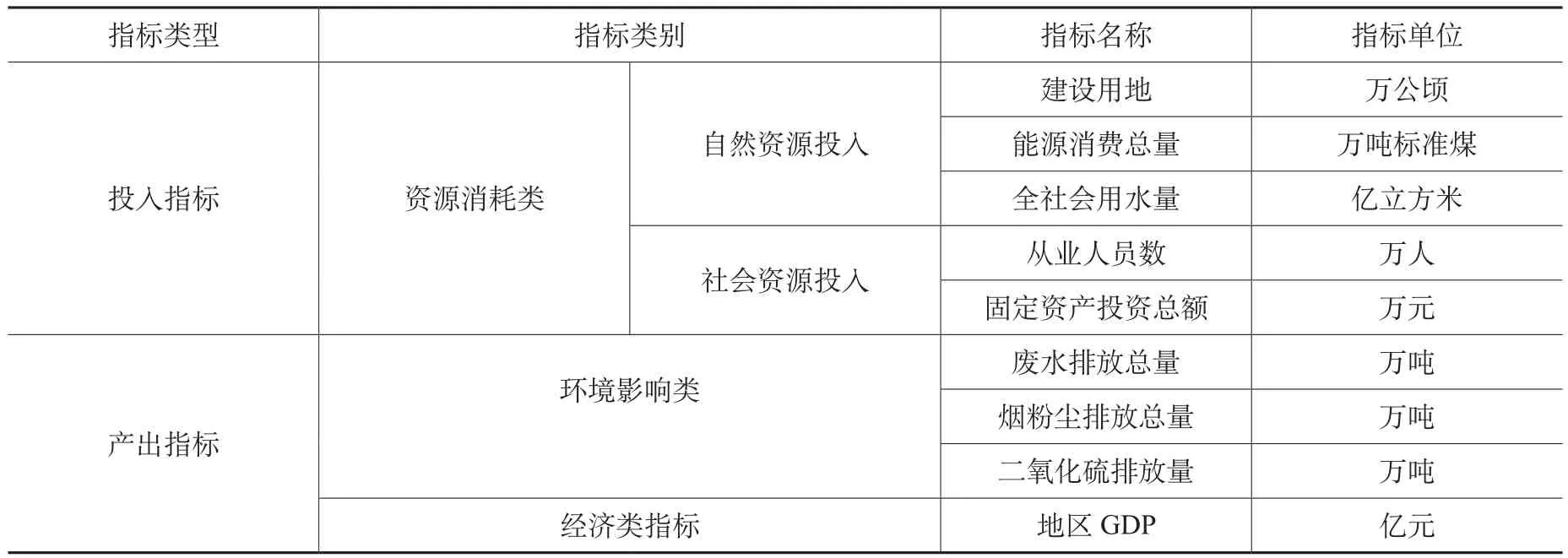
表1 长江经济带生态效率评价指标体系

（三）外界环境变量选取及说明

本文选取各地区产业结构（IS ）、环境政策力度（ER ）和人力资源（EDU）因素作为外界环境变量指标。目前多数学者使用第三产业占地区生产总值的比重表示产业结构发展水平，根据一般理论，第一产业、第三产业、第二产业的能源消耗强度依次递增（毛建素等，2010），仅用第三产业占比衡量产业结构水平明显不够全面。本文综合第二产业和第三产业占比对产业结构水平进行表征：区域产业结构水平=区域第二产业占比*0.4+区域第三产业占比*0.6；选取环境污染治理投资额与地区生产总值的占比作为衡量环境政策力度的指标；用劳动者人均受教育年限对人力资源进行表征，该指标根据各省市6岁及6岁以上人口中文盲、小学、初中、高中和大专以上的抽样数据占比进行加权平均得到，借鉴康继军等（2007）的做法，将文盲、小学、初中、高中和大专以上受教育时间分别设为0年、6年、9年、12年和16年，从而人均受教育年限=（6岁及6岁以上人口中）小学文化人数占比*6+初中文化程度人数占比*9+高中文化程度人数占比*12+大专以上文化程度人数占比*16。

数据均来源于2005-2016年《中国统计年鉴》、《中国能源统计年鉴》、《中国环境统计年鉴》、《中国城市统计年鉴》或国家统计局、环保部和各省区市统计局网站。

四、实证结果分析

（一）长江经济带生态效率评价

1. 第一阶段——超效率DEA模型的ML指数法

本阶段使用软件MaxDEA6.17，在不考虑外界环境因素和随机误差因素的情况下，测度长江经济带生态效率指数（ML指数）及其分解项，如表2和图1所示。

表2 长江经济带第一阶段ML指数

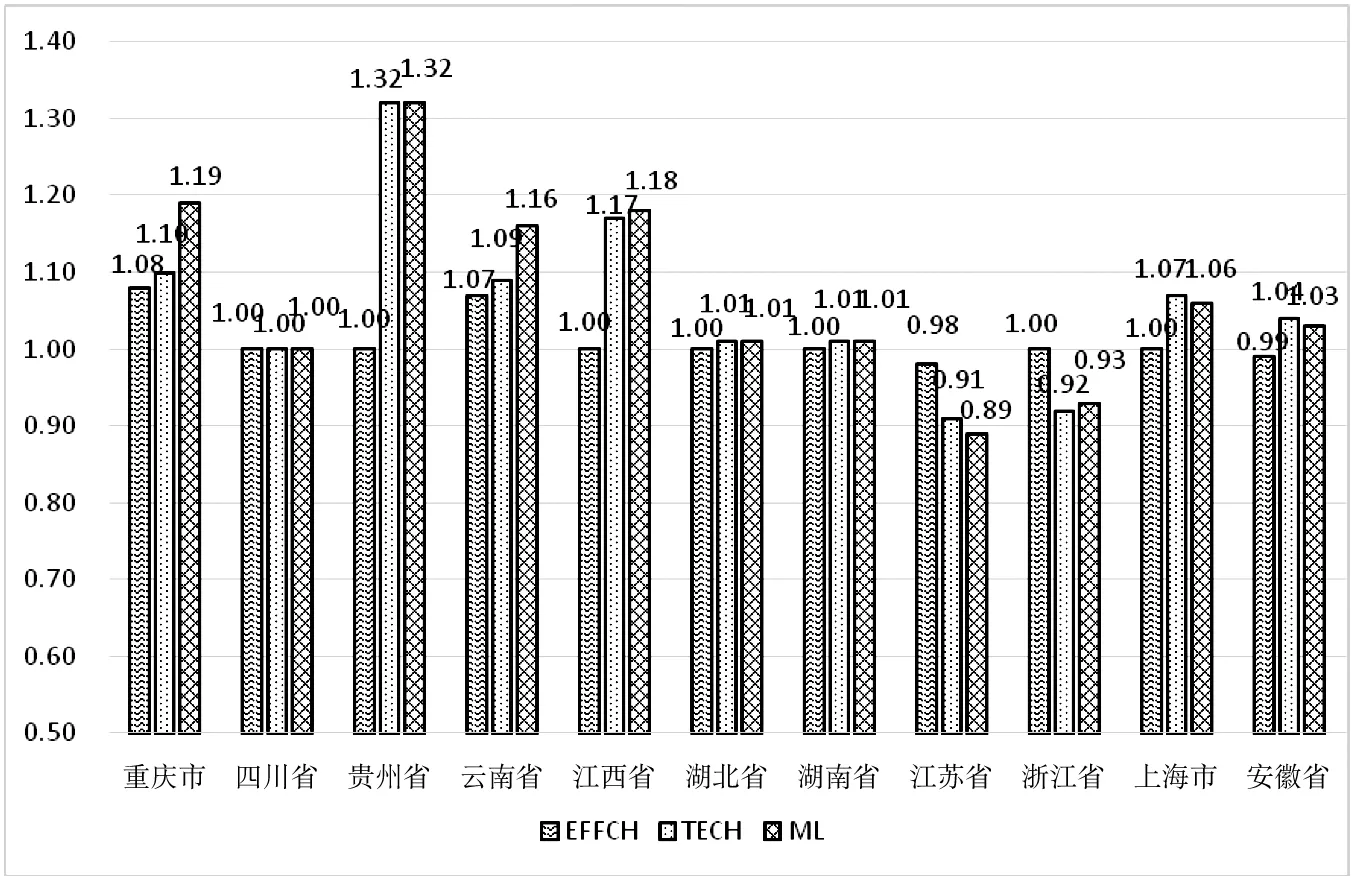
图1 第一阶段ML指数及其分解项

从表1生态效率均值看，长江经济带生态效率水平的地区差异显著，上、中、下游流域分布不均衡。整体ML指数增长率为6%，三大流域中上游达16%，居于首位。从图1看出，上游四个省市生态效率提高的主要原因在于技术进步的贡献，上游地理位置优越，自然资源禀赋较高，拥有较好的生态效率水平。从省际视角看，贵州生态效率在11个省市中排名第一，均值为1.32，重庆和江西生态效率分居二、三名，技术进步率分别为10%和17%。研究表明，中游生态效率增速较缓，年均仅6%，下游生态效率水平退化，降幅年均2%，未达有效前沿。江苏省和浙江省生态效率指数均未能到达有效，需要引起关注。此阶段未考虑外界环境因素和随机误差因素对生态效率值的影响，因此可能存在分析偏误。

2. 第二阶段——SFA回归分析

将第一阶段投入产出指标的松弛值作被解释变量，所选三个外界环境变量作解释变量，利用软件Frontier 4.1建立基于SFA面板数据的回归模型，回归分析结果如表3和表4。

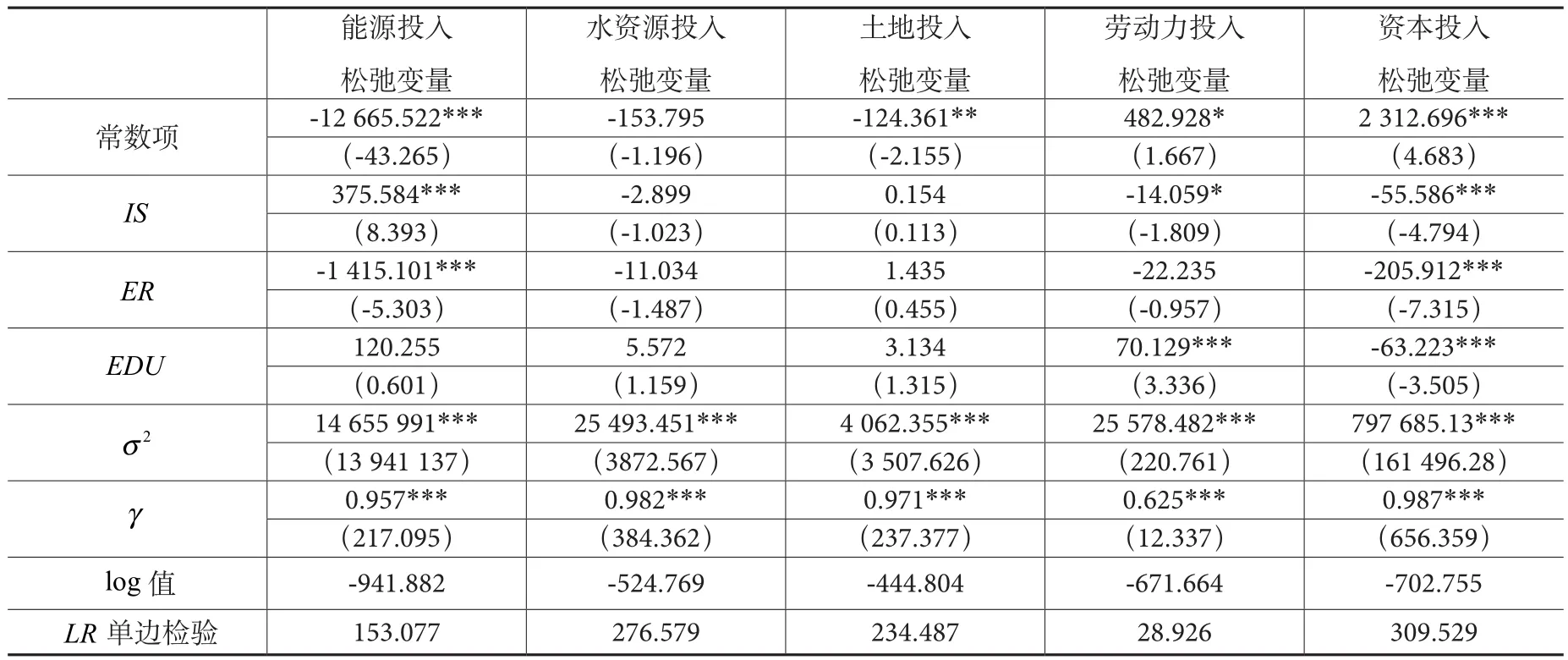
表3 投入松弛变量随机前沿模型回归结果

由表3可知，能源投入、水资源投入、土地投入和资本投入松弛变量的γ值均在1%的显著性水平大于0.9，劳动力投入松弛变量的γ值也在1%的显著性水平下达到0.625，LR单边检验值大于临界值，拒绝不存在管理无效率的原假设，说明管理无效率因素对5种投入的影响占主导地位。其次，三种环境变量对除劳动力投入松弛变量的4种投入的系数大多能够通过显著性检验，说明外界环境因素对长江经济带的生态投入松弛的确存在显著影响。

进一步考察外界环境变量与投入松弛量的关系，IS对劳动力投入和资本投入松弛变量的系数显著为负。表明产业结构水平的提高能有效减少劳动力和资本投入的浪费，进而提高生态效率。这与实际是吻合的，提高产业结构水平，促进产业结构优化升级并逐步高级化发展，对提高生态效率水平有重要推动作用。研究期间，我国三次产业占比从大到小一直保持二、三、一的格局，虽然现阶段我国第二产业占比较高，但近年来第二产业中的高能耗、高污染行业开始进行产业转型，致力于向生产清洁产品转变。同时注意到，IS对能源投入松弛变量系数显著为正，表明产业结构水平的提高将增加能源消耗总量，并不利于生态效率的提高，很大程度是由于第二产业拥有较多高能耗行业，在生产过程中产生巨大的能源消耗，对生态效率水平造成消极影响。IS对水资源投入和土地投入松弛变量的系数未通过显著性检验，说明IS 对水资源和土地资源的影响可以忽略。ER对能源投入和资本投入松弛变量的系数均在1%的显著性水平为负，表明环境污染治理投资的增加能减少能源和资本投入的浪费，促进生态效率提升，这与经验分析结论保持一致。ER对其他3个松弛变量无显著影响。EDU变量理应促进生态效率水平提升，教育程度的加深增强环保意识，进而减少污染物排放，提高生态环境质量，但是经验分析并未支持该假设。EDU对能源投入、水资源投入和土地投入松弛变量的系数不显著，对资本投入松弛变量系数显著为负，对劳动力投入松弛变量的系数显著为正，表明受教育程度的提高能减少资本浪费，增加就业人数，但这并未提升生态效率水平。

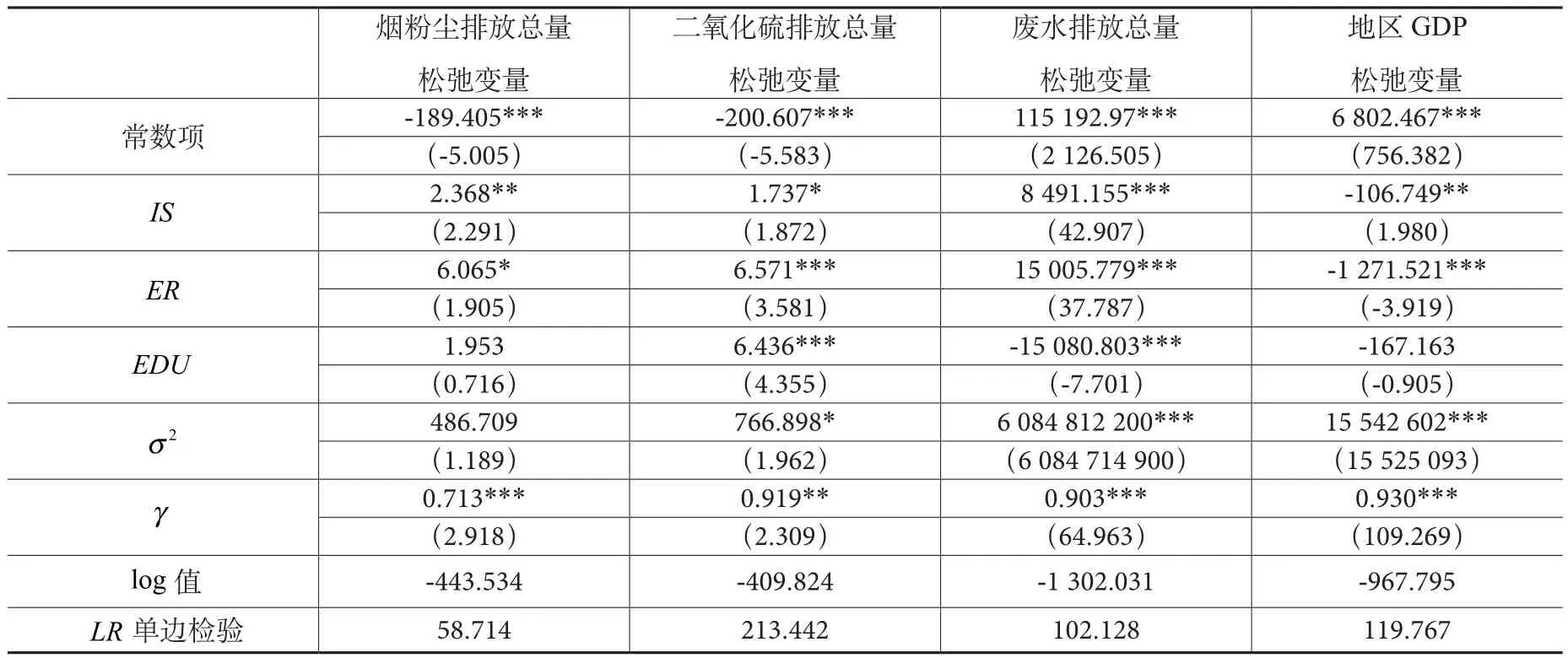
表4 产出松弛变量随机前沿模型回归结果

由表4可知，废水排放总量、二氧化硫排放总量和地区GDP的松弛变量γ值在5%的显著性水平下超过0.9。烟尘排放总量松弛变量γ值也在1%的显著性水平下超过0.7，LR单边检验值大于临界值，说明管理因素对这4种产出变量的影响占据主导地位。其次，IS、ER和EDU对4种产出松弛变量的系数多数能通过显著性检验，说明外界环境因素对长江经济带的生态产出松弛也存在显著影响。IS 对烟粉尘、二氧化硫和废水排放的松弛变量的系数显著为正，说明产业结构水平的提高将增加烟粉尘、二氧化硫及废水排放量，对生态效率产生不利影响，IS对地区GDP的系数显著为负，该指标水平的提升有利于减少地区GDP的冗余，提升生态效率水平。ER的提高理论上讲应促进生态效率改善，但实证结果显示该变量与各产出松弛变量的系数均显著为正，说明长江经济带的环保投入并没有减少烟粉尘、二氧化硫和废水的排放量，环境污染治理投资对生态效率改进的作用非常微弱。因此，在注重增加环境污染治理投资的同时，更加需要重视对投资使用效率的提高，让环境污染治理投资发挥更加积极的作用。EDU对烟粉尘排放和地区生产总值的松弛变量影响不显著，可以忽略。EDU对废水排放和二氧化硫排放松弛变量的系数在1%的显著性水平下为负，表明随着平均受教育年限的增加，将减少废水和二氧化硫的排放量，有利于改善生态效率水平。

从以上分析能够看出，外界环境因素对长江经济带不同省市的影响不同，这很可能导致一些面临较好经营环境或运气的地区拥有较高生态效率，而处在较差经营环境或运气的地区表现出较差的生态效率。因此，进行第二阶段的调整，将长江经济带11个省市置于相同的经营环境和运气之下，对考察真实的生态效率水平具有重要意义。

3.第三阶段——调整后的DEA实证结果分析

第三阶段使用调整后的投入产出数据，测得ML指数及其分解项的动态变化，结果如表5、表6和图2、图3所示。

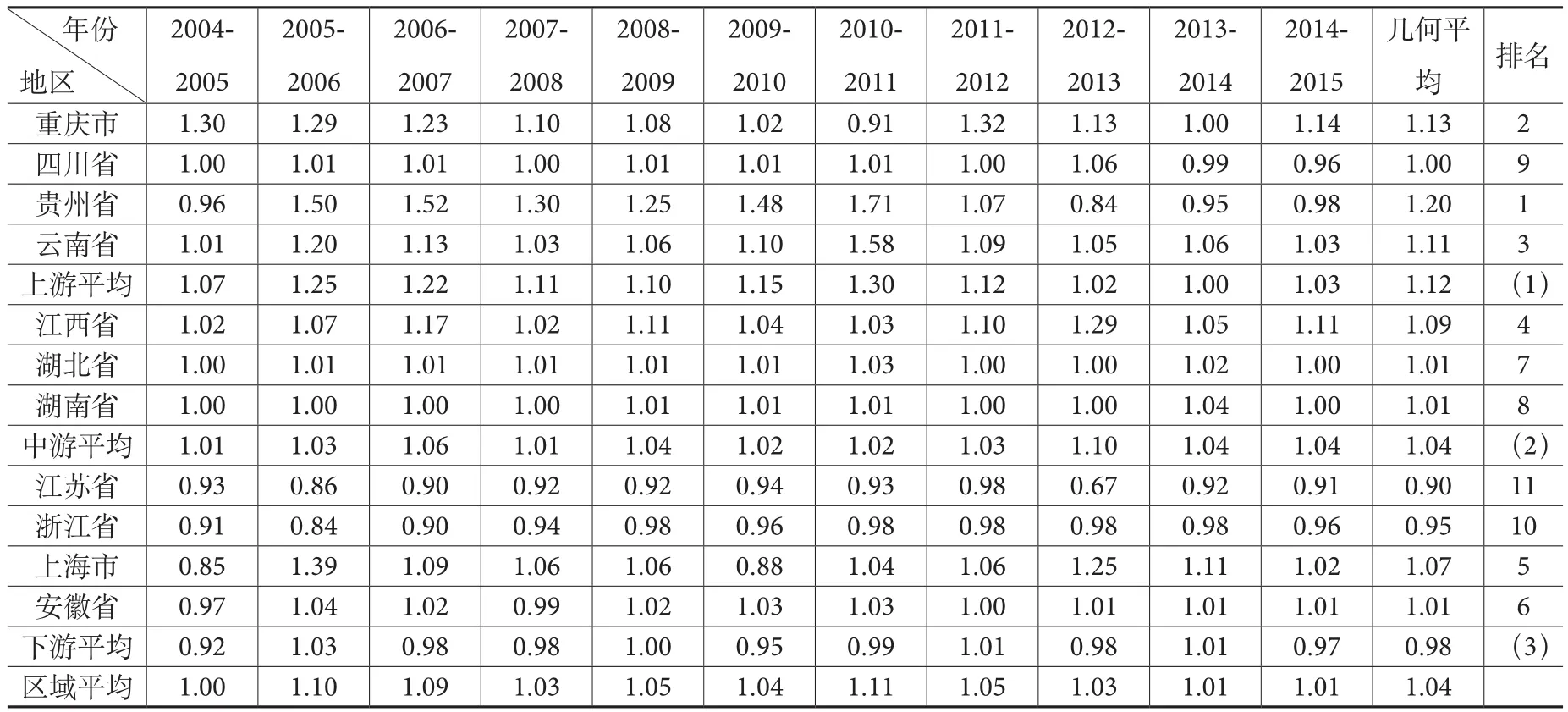
表5 长江经济带第三阶段ML指数

从总体看，调整后整体生态效率从年均增长6%降低至4%，上游从16%下降至12%，中游从6%减少到4%，下游几乎没有变化，说明上、中游处于较好的外界环境和运气状态，其调整前较高的生态效率并非因为较高的管理技术水平，下游生态效率受外界环境因素和随机干扰的影响较小。从图2能够清楚地看到，上游调整前后ML指数变动较大，表明上游受外界环境和随机干扰的影响程度较大。从省际视角看，云南和江西排位互换，说明江西较云南具有较好的外界环境和运气状态，调整至相同状态后的生态效率不如云南。从表6及图3看出，重庆、贵州、云南、江西和安徽的ML指数、EFFCH指数、TECH指数均发生不同程度下降，浙江EFFCH指数下降而TECH指数上升，ML指数从0.93上升至0.95，江苏EFFCH指数上升0.1，上海EFFCH指数下降0.1，其他省市的各指数未发生变动。

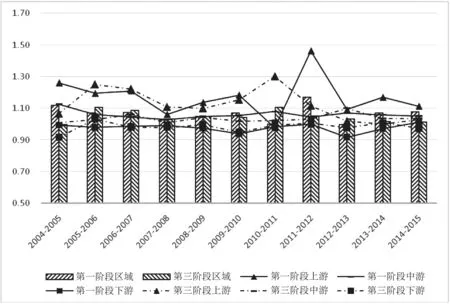
图2 第一阶段与第三阶段ML指数对比图

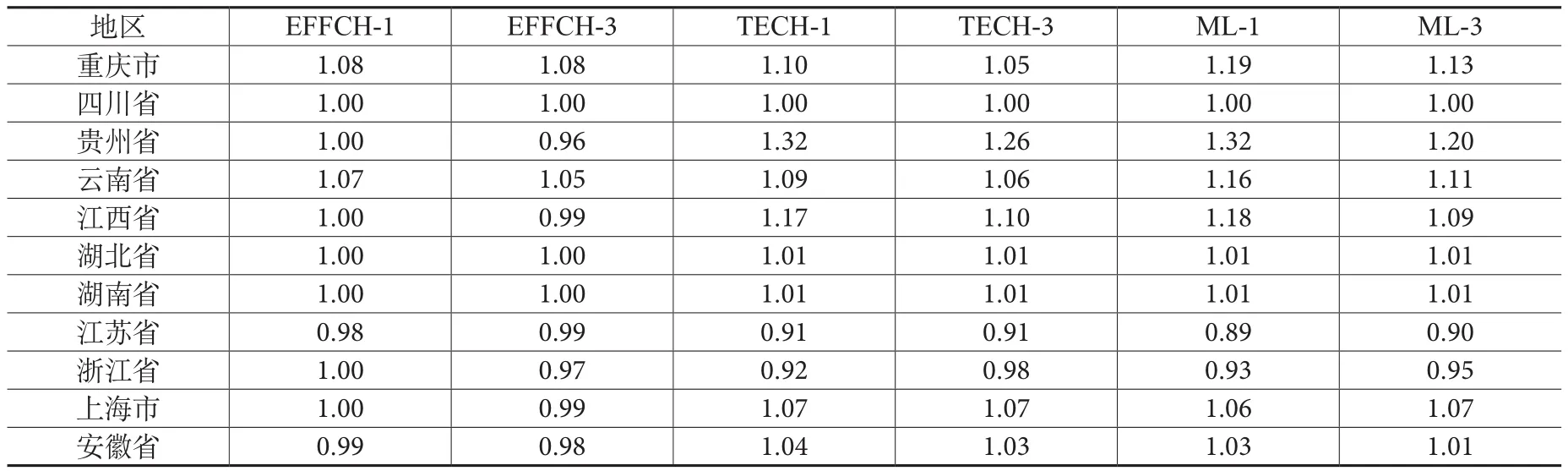
表6 第一阶段与第三阶段ML指数及其分解

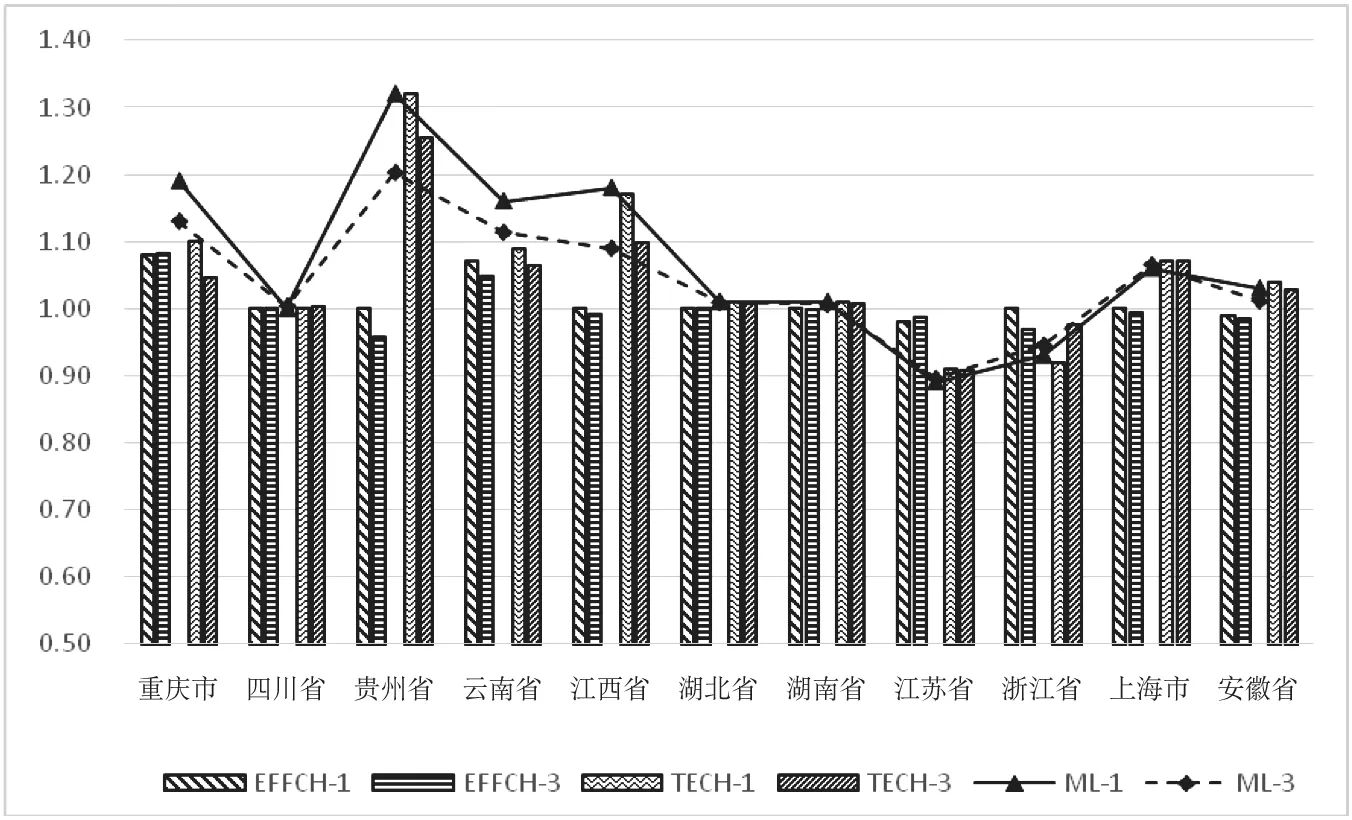
图3 第一阶段与第三阶段ML指数及其分解对比图

（二）长江经济带生态效率收敛性分析

本小节借鉴Barro（1990）和Sala-I-Martin（1992）对经济增长收敛性的基本思想，从σ收敛、绝对β收敛和条件β收敛对长江经济带生态效率差异的变动趋势进行研究。

1. 生态效率σ收敛

采用标准差对区域生态效率σ收敛进行衡量，如下式（6）所示：

其中，Ii(t)为第i 个区域第t 年的生态效率值，N 为区域的数目。如果σ值表现为逐年减小，则趋于σ收敛，反之，则趋于σ发散。

图4给出长江经济带整体及上中下游生态效率σ收敛变化趋势。从整体层面看，长江经济带生态效率标准差从2005年到2012年呈现逐年上升的态势，未表现出σ收敛；从2012年开始，标准差逐步减小，表现出σ收敛趋势；从总体看不存在σ收敛。长江经济带上游4个省市生态效率标准差的变化趋势与整体变动表现一致，总体看也不存在σ收敛。中游3个省市和下游4个省市的生态效率标准差变化状况一致，均表现为逐年增加的趋势，研究期间未表现出σ收敛的态势。从整体及三大流域生态效率标准差的比较来看，上游生态效率标准差远远高于中、下游，也高于整体生态效率的标准差，这表明上游生态效率区域差异性最大，中游和下游生态效率的标准差较为接近，表明中、下游生态效率差异性表现相当。

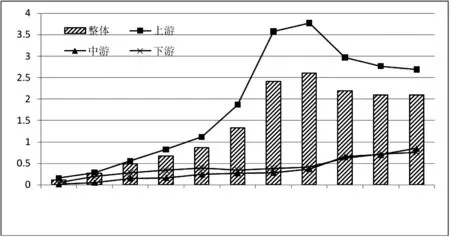
图4 生态效率σ收敛变化趋势

2. 生态效率绝对β收敛

生态效率绝对β收敛要求不同区域之间具有相同的基本特征，即不同的区域具有相似的经济发展速度、产业结构、环境政策、人力资源、能源消费结构和外商投资等，在具有这些相同基本特征的情况下，不同区域生态效率将趋于相同的稳态。用如下检验方程式（7）表示绝对β收敛：

其中，Ii,t和Ii,t+T分别表示第i 个区域第t 期和t+T 期的生态效率值；ln(Ii,t+TIi,t)T 表示从第t 期至t+T 期生态效率的年平均增长率；a 为常数项；b 为基期生态效率值的系数；µi,t为随机误差项。若b显著为负，表示生态效率的增长速度与初始值呈负相关，生态效率较低的省市对生态效率较高的省市具有“追赶”的趋势，即存在绝对β收敛，反之则不存在绝对β收敛。为了最大效用地利用样本数据，同时使计量回归的时间序列表现出连续性，令T=1。

表7给出长江经济带整体及上中下游生态效率绝对β收敛回归的检验结果。从整体层面看，期初生态效率系数估计值b 显著为负，说明整体生态效率存在绝对β收敛，即长江经济带11个省市生态效率趋向于一个共同的稳态。从上中下游看，仅上游区域的b值在1%的显著性水平为负，说明上游4个省市间生态效率表现出绝对β收敛的趋势，期初生态效率水平较低的地区对较高地区具有“追赶”效应，最终达到一个稳定状态。对于中、下游来说，b值并不显著，说明中、下游生态效率不存在绝对β收敛，即这两个区域各省市间生态效率的差距既未呈现缩小趋势，也未呈现发散趋势。

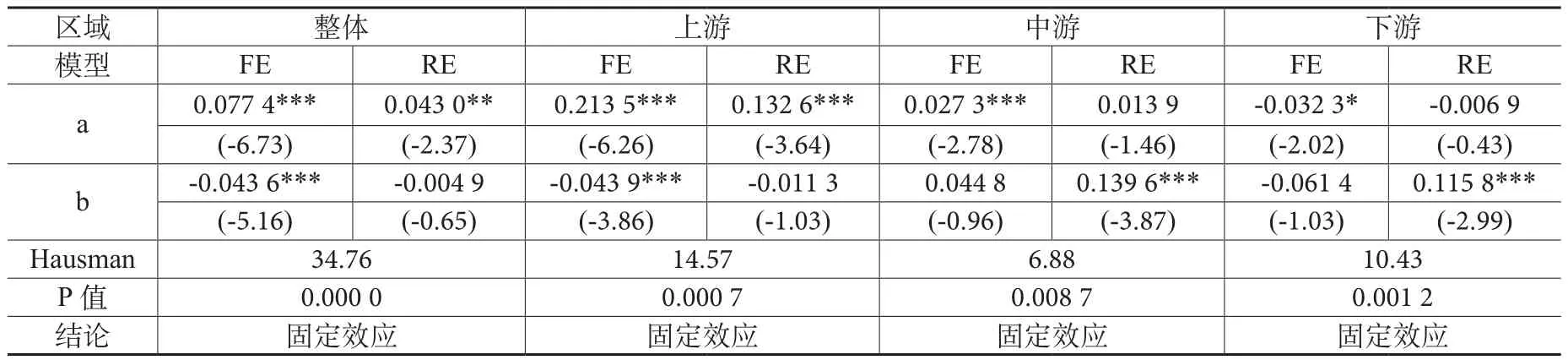
表7 生态效率绝对β收敛回归结果

3. 生态效率条件β收敛

生态效率条件β收敛不再要求不同区域具有相同基本特征，即不同区域可以处于不同的增长路径和稳态水平。如果存在条件β收敛，则最终凭借自身特征收敛于各自的稳态。根据Sala-IMartin&Xavier X（1996）的研究，条件β收敛检验方程式如下：

本文分别从经济发展速度、外资利用、产业结构、环境规制、能源消费结构和人力资源六个方面对长江经济带整体生态效率的条件β收敛进行考察，研究哪些因素促使生态效率到达条件β收敛状态。其中，经济发展速度（gdprate ）使用地区生产总值增长率作为代理变量；外资利用（fdi ）使用实际利用外商直接投资额占地区生产总值的比重表示，美元单位按照当年平均外汇价格换算成人民币；能源消费结构（ecs ）选取煤炭消费量占能源消费总量的份额；产业结构（is）、环境规制（er ）、人力资源（hr）指标与上文产业结构、环境污染治理投资占比和人均受教育年限所使用的数据一致。

表8给出6个控制变量的条件β收敛回归结果。模型一将六个控制变量纳入回归方程，回归结果中b值显著为负，说明将选取的六个指标作为控制变量的情况下，长江经济带生态效率存在条件β收敛。从控制变量的系数估计值看，gdprate、is和ecs三个控制变量可以作为生态效率条件β收敛的影响因素，其中，gdprate和is回归系数的估计值显著为正，说明经济发展速度的提高和产业结构调整对长江经济带生态效率的条件β收敛有显著正向促进作用，ecs回归系数的估计值显著为负，表明该影响因素不利于长江经济带生态效率条件β收敛。同时注意到，fdi、er和hr的回归系数不显著，说明在模型一中，这三个控制变量对长江经济带生态效率的条件β收敛无明显促进作用。模型二剔除fdi、er和hr三个变量，仅考虑gdprate、is和ecs三个控制变量对生态效率条件β收敛的影响，结果显示这三个影响因素的显著性加强，进一步验证了经济发展速度、产业结构和能源消费结构是长江经济带生态效率条件β收敛的重要影响因素。

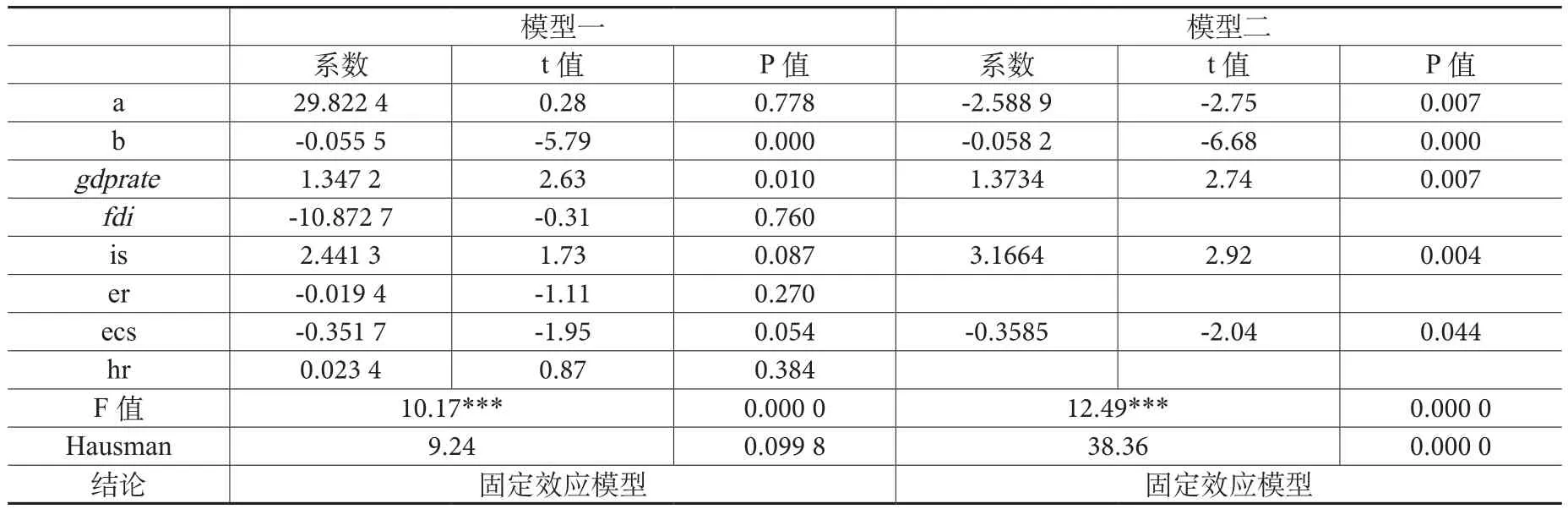
表8 生态效率条件β收敛回归结果

五、结论及启示

第一，因地制宜推进生态文明建设。长江经济带各区域生态效率水平存在较大差异，应结合区域发展状况制定相应政策和措施。遵循“分区推进、适度开发、协调发展”的原则，从各省市生态特点出发，对经济发达且拥有较高生态效率的地区，如上海，重点关注其经济—资源—环境协调发展的可持续性；对经济较为发达但不具备较高生态效率的地区，如江苏、浙江，不仅关注技术进步，更应注重技术效率的提升；欠发达地区也需因地制宜，对拥有较高资源禀赋且拥有较高生态效率的地区，如贵州、重庆、云南、江西等，应充分利用其地理优势保证生态效率水平的稳固提升；对不具有先天优势且生态效率较低的地区，如湖南、湖北、四川等，不应片面追求高生态效率，其首要任务应在于优化资源配置、改善生产力空间布局、推进资源环境可承载的特色产业发展，同时积极引进先进的技术，推进技术进步，从而有效提高生态效率。

第二，坚持优化能源消费结构。能源消费结构对长江经济带生态效率的改善具有抑制效用，长江经济带省市产业结构多以第二产业为主，煤炭化石燃料是第二产业主要的能源消费来源，这必然不利于长江经济带生态效率提升。各地区一方面应重点关注高新技术产业发展，推动传统产业改造升级，另一方面降低化石燃料能源消费比重，提高能源利用效率，同时积极开发清洁能源。对传统支柱产业中高耗能的生产设备，应加快生产工艺技术设备的改造更新，加大节能降耗技术的研发。对新建项目要严格把关，提高高能耗、高污染项目的准入门槛，逐渐淘汰落后产能和行业。

第三，积极推进人力资源水平提高。人均受教育年限的增加将提高全社会环保意识，促进全社会环保技术水平提高，增加资源的循环利用率，减少环境污染，最终推进生态效率提升。本文实证结果显示长江经济带人力资源对生态效率的正向促进作用并不显著，因此需要培养形成正确的生态环保意识，减少日常生活中破坏生态的行为。人力资源的提高一方面对产业结构向生态发展转型具有重要作用，能够为产业结构调整提供全面的技术支持和后备力量，另一方面也能推动经济增长方式转变，从粗放型的经济增长方式向集约型的经济增长方式转变，最终提高长江经济带生态效率水平。

[1] 李春艳, 文传浩. 长江经济带合作共赢的理论与实践探索——“长江经济带高峰论坛”学术研讨会观点综述[J]. 中国工业经济, 2015, (02): 44-49.

[2] 李胜兰,初善冰,申晨. 地方政府竞争、环境规制与区域生态效率[J]. 世界经济, 2014, (04): 88-110.

[3] 黄建欢,杨晓光,成刚,汪寿阳. 生态效率视角下的资源诅咒：资源开发型和资源利用型区域的对比[J]. 中国管理科学,2015,(01):34-42.

[4] 彭红松,章锦河,韩娅,汤国荣,张瑜. 旅游地生态效率测度的SBM-DEA模型及实证分析[J]. 生态学报, 2017, (02):628-638.

[5] 邓波,张学军,郭军华. 基于三阶段DEA模型的区域生态效率研究[J]. 中国软科学, 2011, (01): 92-99.

[6] 华坚, 任俊, 徐敏, Eric Fong. 基于三阶段DEA的中国区域二氧化碳排放绩效评价研究[J]. 资源科学, 2013, (07):1447-1454.

[7] 蓝虹,穆争社. 我国农村信用社改革绩效评价——基于三阶段DEA模型Malmquist指数分析法[J]. 金融研究, 2016,(06): 159-175.

[8] 罗登跃. 三阶段DEA模型管理无效率估计注记[J]. 统计研究, 2012, (04): 104-107.

[9] 张军, 章元. 对中国资本存量K的再估计[J]. 经济研究, 2003, (07): 35-43.

[10] 卢丽文,宋德勇,李小帆.长江经济带城市发展绿色效率研究[J]. 中国人口·资源与环境, 2016, (06): 35-42.

[11] 毛建素, 曾润, 杜艳春, 姜畔. 中国工业行业的生态效率[J]. 环境科学, 2010, (11): 2788-2794.

[12] 康继军, 张宗益, 傅蕴英. 中国经济转型与增长[J]. 管理世界, 2007, (01): 7-17.

[13] Seiford L M, Zhu J. Modeling Undesirable Factors in Efficiency Evaluation [J]. European Journal of Operational Research, 2002, 142(1): 16-20.

[14] WBCSD. Eco-efficient leadership for improved economic and environmental performance [M]. Geneva: WBCSD,1996: 3-16.

[15] Schaltegger S, Sturm A. Ökologische Rationalität: Ansatzpunkte zur Ausgestaltung von ökologieorientierten Managementinstrumenten [J]. Die Unternehmung, 1990, 44(4):273-290.

[16] Common M S. Taxation and the Environment: Complementary Policies : Organization for Economic Cooperation and Development Paris, Organization for Economic Cooperation and Development, 1993, reprinted 1994, 116 pp [J].Resources Policy, 2004, 20(4).

[17] Höh H, Schoer K, Seibel S. Eco-efficiency Indicators in German Environmental Economic Accounting [J]. Statistical Journal of the United Nations Economic Commission for Europe, 2002, 19: 41-52.

[18] Michelsen O, Fet A M, Dahlsrud A. Eco-efficiency in extended supply chains: A case study of furniture production[J].Journal of Environmental Management, 2006, 79(3):290-7.

[19] Dyckhoff H, Allen K. Measuring Ecological Efficiency with Data Envelopment Analysis (DEA) [J]. European Journal of Operational Research, 2001, 132(2): 312-325.

[20] Hoang V N, Alauddin M. Input-orientated Data Envelopment Analysis Framework for Measuring and Decomposing Economic, Environmental and Ecological Efficiency: An Application to OECD Agriculture [J]. Environmental and Resource Economics, 2012, 51(3): 431-452.

[21] lo Storto C. Ecological Efficiency Based Ranking of Cities: A Combined DEA Cross-Efficiency and Shannon’s Entropy Method [J]. Sustainability, 2016, 8(2): 124.

[22] Fried H O, Lovell C A K, Schmidt S S, et al. Accounting for Environmental Effects and Statistical Noise in Data Envelopment Analysis [J]. Journal of Productivity Analysis, 2002, 17(1): 157-174.

[23] Jondrow J, Lovell C A K, Materov I S, et al. On the Estimation of Technical Inefficiency in the Stochastic Frontier Production Function Model [J]. Journal of Econometrics, 1982, 19(2-3): 233-238.

[24] Barro R J, Sala-I-Martin X. Economic growth and convergence across the United States[J]. Social Science Electronic Publishing, 1990.

[25] Barro R J, Sala-I-Martin X. Convergence[J]. Journal of Political Economy, 1992, (100): 223-251.

[26] Sala-I-Martin X X. The Classical Approach to Convergence Analysis[J]. Economic Journal, 1995, 106(437): 1019-1036.

Ecological Eff i ciency and Convergence Analysis of the Yangtze River Economic Belt

ZHAO Xin1, HU Ying-xue2, SUN Xin1
(1.School of Statistics and Applied Mathematics, Anhui University of Finance and Economics, Bengbu 233030,China;2.UT Business School of Heng Simai, Utah State University, Utah, UT, USA)

Aiming at the shortcomings of the existing efficiency measurement model, using Malmquist -Luenberger index method in three stage super eff i ciency DEA model to calculate the ecological eff i ciency of Yangtze River Economic Belt. At the same time, the convergence of new classical economic growth is used to explore its convergence. The results showed that after adjustment, the overall and upper and middle reaches of the ecological eff i ciency growth rate decreased, the downstream has almost no change. It shows that the upper reaches and the middle reaches are in good external environment and good luck. The external environment variables have signif i cant effects on the input-output slack variables of ecological eff i ciency, and different ways of inf l uence, it is necessary to adjust the second stage. There is no sigma convergence in the ecological eff i ciency of the whole, upper, middle and lower reaches, and there exists absolute beta convergence in the whole and upstream. In the speed of economic development, utilization of foreign capital, industrial structure, environmental regulation, energy consumption structure and human resources six kinds of control variables, the speed of economic development, industrial structure and energy consumption structure are important factors in prompting the existence condition of beta convergence.

the Yangtze River Economic Belt; ecological eff i ciency; three stage super eff i ciency DEA; ML index; convergence

F424.1

A

2095-7572(2017)06-0090-14

2017-10-7

国家自然科学基金（项目编号：71471001；71503001；71301033）；全国统计科学研究项目（项目编号：2016LY26）

赵鑫（1993-），男，安徽淮南人，安徽财经大学统计与应用数学学院硕士研究生，研究方向：环境与能源统计、数量经济；

胡映雪(1996-)， 女，安徽六安人，美国犹他州立大学本科生，研究方向：国际经济与贸易研究；

孙欣（1973-），男，安徽庐江人，博士，安徽财经大学统计与应用数学学院副教授，研究方向：环境与能源统计、数量经济。

﹝执行编辑：周冬﹞