给定直径的单圈图的Harary指数
2017-12-06伊佳茹雷英杰
伊佳茹,雷英杰
(中北大学 理学院, 太原 030051)
给定直径的单圈图的Harary指数
伊佳茹,雷英杰
(中北大学 理学院, 太原 030051)
连通图G的Harary指数是指图G中所有点对的距离的倒数之和。主要研究固定直径的单圈图的极大Harary指数及相对应的极图。特别地,当4≤d≤n-3,且d≡0(mod2)时,得到第二大Harary指数的极图。
Harary指数;直径;单圈图;极图
Harary指数是一种重要的化学类拓扑指数。该指数被提出之后,国内外学者对其进行了深入的研究[1-10],其中:文献[1]研究了给定悬挂点和阶数的单圈图的极大Harary指数;文献[3]找到了固定直径,匹配数和独立点集的简单图的极小Harary指数以及其所对应的极图;文献[4]得到了固定直径的树的第二大Harary指数以及相对应的极图。

1 引理及相关证明


引理2[13]令H是一个连通图,Tl表示阶为l的树,且V(H)∩V(Tl)={v},则有
H(HvTl)≤H(HvK1,l-1)
当且仅当HvTl≅HvK1,l-1等号成立。引理2是文献[14]中定理4的特殊情况。

引理4 令G是一个连通图,uv∈E(G),Gp,q(u,v)是由图G分别在点u连接一条长为P的悬挂路,点v连接一条长为q的悬挂路所得到的。若p≥q≥1,则有
H(Gp,q(u,v))>H(Gp+1,q-1(u,v))
证明记G0=G-{u,v};悬挂路分别为:P=uu1u2…up,Q=vv1v2…vq。将G0图中的点分成3部分:
V1={vid(vi,u)=d(vi,v)}
V2={vid(vi,u)=d(vi,v)+1}
V3={vid(vi,u)+1=d(vi,v)}
则有:
当p≥q≥1时,有


由此易知H(Gp,q(u,v))>H(Gp+1,q-1(u,v))。证明完毕。



图和


则有




图2 U0的d+2阶单圈图




论断1 若i≠d+2,且pi>1,则i∈{k,k+1}。
采用反证法:若i≠d+2,则i∉{k,k+1}。考虑其对称性,只需要考虑k+1 1) 当k V1={v1,v2,…,vk};V2={vk+2,vk+3,…,vd+1};V3={u1,u2,…,upi} 对vx∈V1,vy∈V2,vz∈V3,有如下关系: dG1(vx,vd+2)-dG(vx,vd+2)=1 dG1(vy,vd+2)-dG(vy,vd+2)=-1 dG1(vz,vd+2)-dG(vz,vd+2)=-1 则有 显然有H(G1)-H(G)>0。记圈C=vk1vk1+1vd+2vk1(k1=k+1)是图G1的圈。若vk1+1即为vi,则G1中的点vk1+1上有悬挂点,H(G1)>H(G),矛盾。若k1+1 2) 当k≥d-k时,有i-1>k≥d-k≥d-(i-2)。构造图G1=G-viu1-viu2-…-viupi+vi-1u1+…+vi-1upi,同理可得 由1)和2)可知:论断1得证。 论断2i≠d+2。 采用反证法:若i=d+2,构造图G*=G-vd+2u1-…-vd+2upi+vku1+…+vkupi。同理可得: 显然H(G*)>H(G),矛盾,论断2得证。 论断3k≠d。 采用反证法:若k=d,构造图G*=G-vd+1vd+2+vd-1vd+2,同理可得: 显然H(G*)>H(G),矛盾,论断3得证。 由引理6和引理7,引理8显然成立。 论断5V(Cq)∩V(Pd+1)≠∅。 采用反证法:假设V(Cq)∩V(Pd+1)=∅,因为G连通图,则一定存在一条路Q=vivkvk+1…vl-1vl连接圈和诱导路,vi∈V(Cq),vl∈V(Pd+1)且vk…vl-1∈V(G)/(V(Cq)∪V(Pd+1)),令u1,u2,…,ud(vl)-1∈N(vl)/{vl-1}。构造图G*=G-vlu1-…-vlud(vl)-1+viu1+…+viud(vl)-1,由引理1可得H(G*)>H(G),矛盾。 论断6 对于v∈V(G)/(V(Cq)∪V(Pd+1)),有d(v)=1,且这些点都悬挂在圈或路的同一个点上。 证明由引理2和引理1,对于v∈V(G)/(V(Cq)∪V(Pd+1))的所有点,一定以树的形式连接在圈或者路上边,论断6得证。 论断7k≠l。 采用反证法:假设k=l,其中vd+2、vk+1、vk+2一定存在。 记u1,u2,…,ud(vd+2)-1∈NG(vd+2)/vk,悬挂点的邻点为vm,悬挂点的个数为pm。构造图G*=G-vd+2u1-…-vd+2ud(vd+2)-1+vk+1u1+…+vk+1ud(vd+2)-1。 记V1=vi:vi∈Cq/{vk}且dvi,vd+2 dG*(vx,vd+2)-dG(vx,vd+2)=2;dG*(vx,vz)-dG(vx,vz)=-2; dG*(vy,vd+2)-dG(vy,vd+2)=1;dG*(vy,vz)-dG(vy,vz)=-1 当vm∈V1时有 记: 当vm∈V2时有 当vm∈V3时有 当vm为vd+2时有 综上可得H(G*)>H(G),矛盾。若围长g为偶数,同理H(G*)>H(G),论断7得证。 论断8 若l=k+1,那么s-d=2;若l≥k+2,那么s-d=l-k。 采用反证法:否则s-d>l-k≥3,其中vd+3一定存在,且l≥k+2,则vl-1一定存在。 记u1,u2,…,udG(vd+2)-1∈NG(vd+2)/{vl}。构造图G*=G-vd+2u1-vd+2u2-…-vd+2udG(vd+2)-1+vlu1+vlu2+…+vludG(vd+2)-1。记V1={vi:vi∈Cq/{vk,vk+1,…,vl,vd+2},且d(vi,vk) dG*(vx,vy)-dG(vx,vy)=-1 若图G中的圈为偶圈,记V3={vi:vi∈Cq/{vk,vk+1,…,vl},且dG*(vi,vd+2) dG*vz,vm-dGvz,vm=-1 显然有H(G*)>H(G),矛盾。 dG*vz,vm-dGvz,vm=-1 显然有H(G*)>H(G),矛盾。论断8得证。 论断9l=k+1。 证明假设l≠k+1,由论断4可知s-d=l-k,不妨设悬挂点都在Pd+1的点vi上,悬挂点为u1,u2,…,um,由于对称性,只对vl和vi的位置进行讨论。 1) 若l=i,构造G*=G-vlvd+2-vd+2vd+3-vlu1-…-vlum+vl-1vd+2+vl-1vd+3+vl-1u1+vl-1um,则有 由于l-k≥5,显然H(G*)>H(G)成立,矛盾。 2) 若i>l,构造图G*=G-vlvd+2-vd+2vd+3+vl-1vd+2+vl-1vd+3,则有 得H(G*)>H(G),矛盾。 3) 若k 得H(G*)>H(G),矛盾。 由定理1和引理9,以下定理显然成立: [1] CAI G X,GUIDONG Y U,XING B H.Harary index of unicyclic graphs with n vertices and k pendent vertices[J].华东师范大学学报(自然科学版),2015,2015(1):120-125. [2] XU Kexiang,KINKAR C D.On harary index of graphs[J].Discrete Applied Mathematics,2011,159: 1631-1640. [3] FENG L,LAN Y,LIU W,et al.Minimal Harary Index of Graphs with Small Parameters[J].MATCH Commun.Math.Comput.Chem.2016,76(1):23-42. [4] 肖金环,赵飚.固定直径的树的Harary指数[J].曲阜师范大学学报(自然科学版),2014(3):30- 34. [5] HE Changxing,CHEN Ping,WUA Baofeng.The Harary Index of a Graph Under Perturabation[J].Discrete Math- matics,Algorithms and Applications,2010,2(2):247-255. [6] XING Baohua,CAI Gaixiang.The Wiener index of trees with prescribed diameter[J].Operations Research Transactions,2011,15(4):36-44. [8] LI Xiaoxia.On the extremal wiener index of some graphs[J].Operations Research Transactions,2010,14(2):55-60. [9] CHEN Yahong,ZHANG Xiaodong.The Wiener index of unicycle graphs with girth and the matching number[J].Mathematics,2011(2):1-15. [11] BONDY A,MMURTY U S R.Graph Theory with Application[M].New York:Macmillan Press,1976. [12] XU Kexiang,NENAD T.Hyper-wiener and Harary indices of graphs with cut edges[J].Utilitas Math,2011,84:153-163. [13] 陈单单.单圈图的Harary指数[D].长沙:湖南师范大学,2009. [14] HE C X,CHEN P,WU B F.The Harary index of a graph under perturbation[J].Discrete Mathematics Algorithms & Applications,2010,2(2):247-255. (责任编辑刘 舸) OntheHararyIndexofUnicycleGraphswithGivenDiameter YI Jiaru (School of Science, North University of China, Taiyuan 030051, China) The Harary index is defined as the sum of reciprocals of distance over all pairs of vertices of a connected graph.This paper gives the largest Harary index of unicycle graphs with given diameter and characterizes the extreme graphs attaining the upper bound. Specially, we also obtained the second largest extreme graphs when 4≤d≤n-3 andd≡0(mod2). Harary index;diameter;unicycle graph;extreme graph 2017-05-12 国家自然科学基金资助项目(11301489) 伊佳茹(1993—),女,山西人,硕士研究生,主要从事组合数学研究,E-mail:1045161925@qq.com。 伊佳茹,雷英杰.给定直径的单圈图的Harary指数[J].重庆理工大学学报(自然科学),2017(11):204-210. formatYI Jiaru, LEI Yingjie.On the Harary Index of Unicycle Graphs with Given Diameter[J].Journal of Chongqing University of Technology(Natural Science),2017(11):204-210. 10.3969/j.issn.1674-8425(z).2017.11.031 O157.5 A 1674-8425(2017)11-0204-07




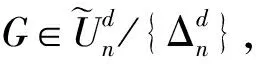
2 主要结论















