1990－2014年武夷山特大暴雨的分形特征分析

纪志荣,何东进,巫丽芸,游巍斌,曹 彦,陈丽琴

(1.福建农林大学计算机与信息学院，福建福州350002；2.福建农林大学林学院，福建福州350002；3.福建农林大学金山学院，福建福州350002)

1990－2014年武夷山特大暴雨的分形特征分析

纪志荣1,何东进2,3∗,巫丽芸2,游巍斌2,曹 彦3,陈丽琴1

(1.福建农林大学计算机与信息学院，福建福州350002；2.福建农林大学林学院，福建福州350002；3.福建农林大学金山学院，福建福州350002)

借助分形与混沌理论,对1990－2014年武夷山特大暴雨降水量的时间序列进行分析,重构其嵌入相空间,得出关联维数和饱和嵌入维数,进而确定了模拟相应动力系统所需的基本变量数目为8。基于R/S分析法计算了Hurst指数为0.8195,表明武夷山特大暴雨降水量的时间序列存在长期记忆性的特征。最后通过加权零阶局域法,对武夷山短期的特大暴雨降水量进行预测。研究结果客观、合理地反映了特大暴雨降水量的分形特征,可为建立特大暴雨降水量的时间序列预报模型提供有力的理论依据。

特大暴雨；分形；关联维数；Hurst指数；加权零阶局域法预测

暴雨降水极易成灾致灾,尤其特大暴雨给人民带来巨大的危害和损失,随着人类活动和全球气候变暖,暴雨洪涝灾害呈现逐年增多增大的趋势。中国是个多暴雨的国家,暴雨洪涝灾害的研究与预防一直是大气科学研究中重要的课题,尤其特大暴雨是业务预报工作难点,因此深入研究暴雨降水的分布及变化特征具有重要意义。

长期以来,我国在暴雨研究中取得了丰硕的成果:姜德娟等(2011),郑腾飞等(2012),李剑锋等(2012),董伟等(2012),史培军等(2016)运用小波分析、DFA法、M-K、数值模拟,空间相关等方法研究山东、江苏、新疆、东北、全国极端降水时空分布特征及变化趋势；连明涛等(2014)分析了河南省多年不同场次特大暴雨的递减指数；冯文等(2015),王坚红等(2014)研究了特大暴雨的动力机制特征；康婷婷等(2012),侯保灯等(2014)针对中国年最大致洪暴雨落区的时间序列进行自相关、趋势、周期等一系列分析,并结合改进的BP网络方法进行模拟与预测。但传统的统计力学模型难以深刻揭示暴雨行为机制,分形理论的出现,为解释复杂系统行为及其预测研究提供了有力的支持。近20 a来,许多学者相继应用分形、混沌理论对水文资源进行研究(Waymire,1985；Foufpula-Georgou et al.,1984；Lovejoy et al.,1985；Keden et al.,1987)。对暴雨分形性质也有一定的研究,Koutsoyiannis等(1997)建立了暴雨过程的单标度模型来研究暴雨的时间分配性质；Menabbde等(1999)将标度不变性的假设引入暴雨公式,建立了暴雨公式的极值分布模型；常福宣等(2002)以四川成都站的长期暴雨资料按分形理论作了分析并进行预测；Michele等(2001)在分形理论的基础上,推导出暴雨随面积而变的折减系数公式；任飞鹏(2016),何佳等(2016)运用R/S研究武汉市、宝鸡市的降水变化特征,徐毅青等(2016)分析了台风暴雨区低频泥石流的分形特征。分形理论应用于暴雨研究取得了一定成果,但用于特大暴雨系统尚不多见。由此,本文尝试运用分形理论,探讨特大暴雨发生系统的分形特征。以1990－2014年武夷山年特大暴雨降水量为研究对象,深入分析降水量的分形特征,并通过加权零阶局域法,对武夷山短期的特大暴雨降水量进行预测,以期为特大暴雨诊断分析、业务预报、防灾指挥等提供理论指导。

1 研究区域概况

武夷山地处中亚热带,境内群山重叠,海拔1 800 m以上的山峰多达三十余座,形成天然屏障,冬季可阻挡或削弱北方冷空气的入侵,具有降水量多,湿度大,雾日长,垂直变化显著等气候特点。武夷山邻区是我国东南主要暴雨区,在华南前讯期及江南梅雨期间,西南气流移动途经武夷山分水岭地带,受山脉阶梯地势地形(1 000－1 500 m,主峰黄岗山2 158 m)丘陵高山的影响与北方冷空气在此交绥,常易出现大暴雨。

2 武夷山特大暴雨降水量的时序特征

2.1 1990－2014年武夷山特大暴雨降水量的时序分布

研究数据来自中国林业科学数据中心。根据中国气象灾害大典,气象部门规定24 h降水量达200 mm及其以上为特大暴雨标准,文章选用1990－2014年武夷山年暴雨降水量的24 h最大值(均超过200 mm,见图1)为代表值,可视为特大暴雨,作为研究对象。图1可见,暴雨降水量最小值为658 mm,最大值为2 455 mm,平均值也达到了1 137.12 mm,武夷山这25 a都经历了特大暴雨,每年的暴雨降水量表现出极强的随机性和不确定性。在1993、1998、2008、2013年都出现了不同程度的峰值。另外利用Eviews软件进行正态性检验,J-B统计量的值为10.96,P值为0.00＜0.05,并不服从正态分布。

2.2 平稳性检验

对序列进行单位根检验,利用Eviews软件在滞后阶数对话框选择SC准则,采用带常数项方程进行ADF检验,在显著性水平0.05下,P值为0.34,接受存在单位根的原假设,武夷山特大暴雨降水量的时间序列是不平稳的,传统的时间序列的方法进行分析不再适用,这对于选取分形分析方法起到了很重要的指导作用。

图1 武夷山1990－2014年特大暴雨降水量时序分布图Figure 1 The sequence chart of extrem rainfall in Wuyi Mountain from 1990 to 2014

3 武夷山特大暴雨降水量序列的分形特征

分形理论系由美国科学家曼德尔布罗特(Mandelbrot,1982)于20世纪70年代中期创立,它是描述具有相似结构的几何形状的工具,分形的特点是通过计算研究对象的分数维数,定量描述其特征。以下从关联维数和R/S分析验证夷山特大暴雨降水量时间序列的分形特征。

3.1 关联维数

关联维数就是从少数甚至单一数据序列提取关于维数信息的方法,可用相空间重构方法(G-P法)计算。

(1)重构相空间

采用时间差法重构相空间,按时间间隔τ而构造出一批矢量:

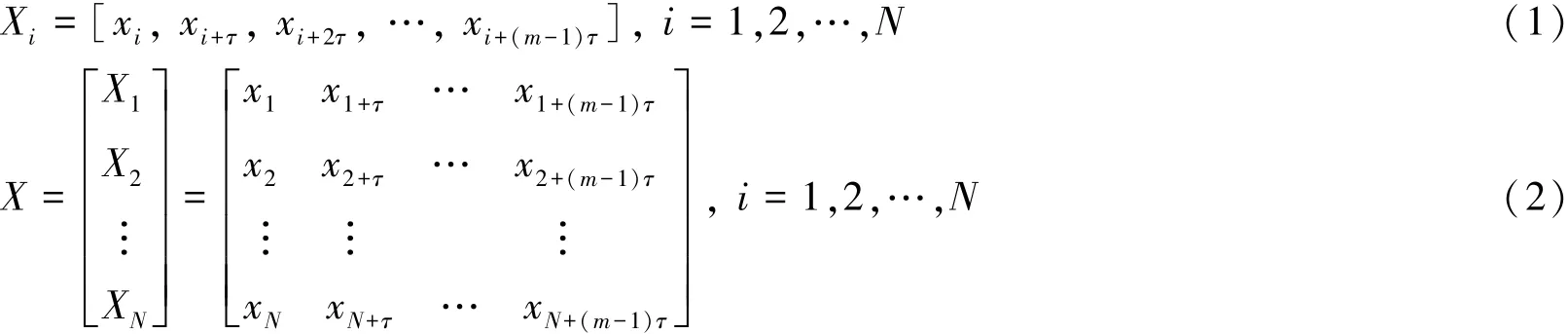
式中,m为嵌入维数(即重构相空间的维数)；Xi为重构相空间矢量；τ为延迟时间；n为原时间序列的点数(或长度)；N为重构后的相空间矢量的个数,N＝n－(m－1)τ。

(2)计算关联函数C(r)

式中,‖Yi－Yj‖为相空间中Ym(ti)与Ym(tj)两点的欧氏距离。

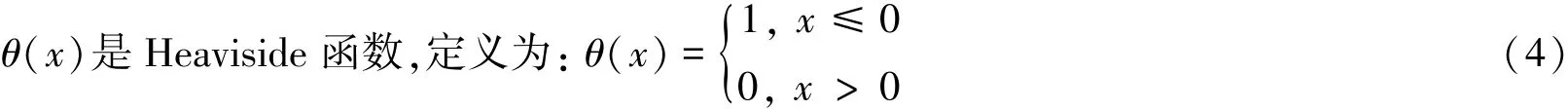
标尺r的选值需适中,太大的r反映不了系统内部的性质,太小的r使得系统中一切偶然的噪声都会表现出来,没有意义。适当调整r,可能在r的一段区间内,C(r)与r存在下列标度关系:

式中,d为关联维数。

显然d与m相关,选取不同的标尺r,得到lnr与lnC(r)的关系图,如存在无标度区,即直线段,表明存在分形特征,直线段的斜率即关联维数。

取τ＝2,做出lnr与lnC(r)的关系图2,可以看出,不同嵌入维m下,lnr与lnC(r)均存在线性相关区域,验证了1990－2014年武夷山特大暴雨降水量的时间序列存在分形特征。为了清晰地看出不同嵌入维下其关联维d的变化特征,作出了嵌入维m与关联维d的关系曲线(图 3)。

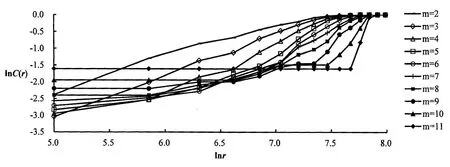
图2 lnC(r)－lnr的曲线图Figure 2 The diagram of lnC(r)－lnr

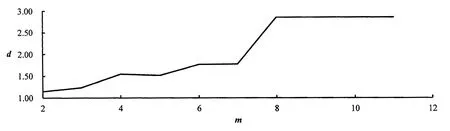
图3 m-d曲线图Figure 3 The diagram of m-d

图3 表明,随着嵌入维数m值增大,关联维数d值不断增大。当m＝8时,关联维数d趋于稳定,达到饱和,称之为饱和关联维数d＝2.85,m＝8为饱和嵌入维,它表征动力系统的有效自由度数目为8个,说明要恰当地描述特大暴雨降水量系统变化特征,进行动力系统建模,至少需要8个独立变量。

3.2 R/S分析

重标极差分析法(rescaled range analysis),简称R/S分析法。是水文学家Hurst在大量实证研究的基础上提出的一种方法,后经过Mandelbrot等人(1969)逐步完善。下面利用重标极差分析法(R/S分析法)研究特大暴雨降水量序列,判断其外在形态上表现出的复杂性特征。主要计算原理:

对于时间序列X＝{X1,X2,…,XN},将X均分为M个相邻的长度为n的子序列,子序列记为 Xj＝ {x(j－1)n＋1,x(j－1)n＋2, …,x(j－1)n＋n},j＝ l,2,…,M。

在双对数[ln(R/S)n,lnn]坐标系中用最小二乘法拟合求得ln(R/S)n＝0.82,lnn＝0.84,R2＝0.97,方程拟合效果很好。Hurst指数为0.82＞0.5,表明特大暴雨降水量具有明显的分形性质,存在持续性的变化特征,具有长期记忆性。

4 武夷山特大暴雨降水量的预测

武夷山特大暴雨降水量存在明显的分形性质,须从混沌的角度去研究其复杂性征。加权零阶局域法将中心点的空间距离作为一个拟合参数引入预测过程。具体算法:首先将时间序列进行零均值处理,得到序列x(t),t＝1,2,…,N；再根据Taken定理选取嵌入维m≥2d＋1,得到重构相空间

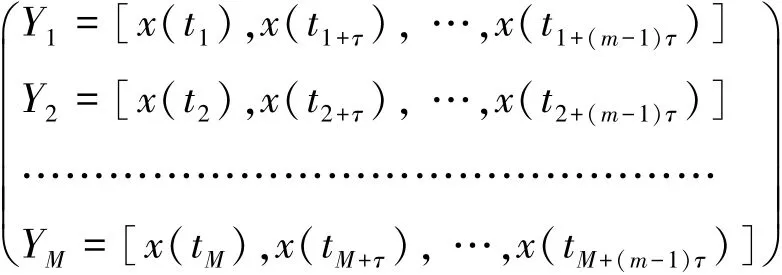
式中,M为重构相空间中点的个数,M＝N－(m－1)τ。在相空间中计算各点到中心点Y(M)之间的欧式距离,找出Y(M)的参考向量集＾Y＝{YM1,YM2,…,YMq}

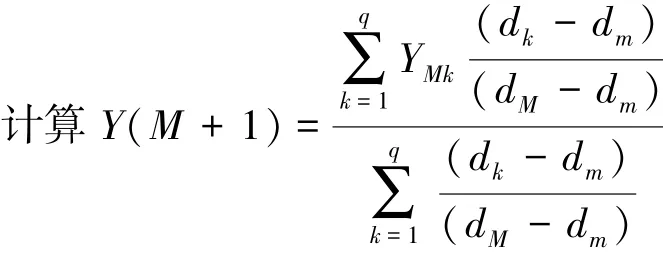
式中,dM是dk中的最大值,dm是dk中的最小值,进而得到x(M＋1)的预测结果。

预测值与实际值具有较好的一致性,二者走势一致,相对误差比率大部分在10%的范围以内,预测精度较高。

表1 2010－2014年武夷山特大暴雨降水量的预测Table 1 The forecast results of extrem rainfall in Wuyi Mountain from 2010 to 2014

5 结论与讨论

武夷山邻区是我国东南主要暴雨区,在1990－2014年的25 a中,每年都会出现特大暴雨,为了避免特大暴雨造成洪涝灾害与山洪危险,进行及时有效的预测、预报尤为重要,对武夷山防洪减灾以及经济持续发展具有重大意义。文章通过对1990－2014年武夷山特大暴雨降水量时间序列的研究,论证了其在相空间的运动是混沌运动,关联维数为2.85,饱和关联维所对应的嵌入相空间的最小维数m＝8,要恰当地描述特大暴雨降水量的系统变化特征,需构造至少8个独立变量的动力学系统。R/S分析表明武夷山特大暴雨降水量具有持续性的变化特征,与加权零阶局域法预测结果一致,且精度较高。研究结果表明,分形理论是进行特大暴雨系统研究的有效途径,文章的研究加深了对暴雨灾害特征及其发生机理的认识,为建立暴雨大尺度时序预报奠定了基础。同时,为深刻揭示暴雨变化不同时段的演化历程,未来可借助动力系统重建及多重分形理论,进一步分析形成暴雨分形结构特征的动力学过程。

常福宣,丁晶,姚健,2002.降雨随历时变化标度性质的探讨[J].长江流域资源与环境,11(1):79-83.

董伟,刘海峰,朱玉祥,2012.吉林省夏季极端降水事件特征分析[J].自然灾害学报,21(4):69-75.

冯文,符式红,赵付竹,2015.近10年海南岛后汛期特大暴雨环流配置及其异常特征[J].气象,41(2):143-152.

姜德娟,李志,王昆,2011.1961－2008年山东省极端降水事件的变化趋势分析[J].地理科学,31(9):1 118-1 124.

康婷婷,陆桂华,侯保灯,2012.中国年最大致洪暴雨落区随机性分析[J].水电能源科学,30(8):1-4.

何佳,杨荣,周旗,等,2016.1960－2013年宝鸡市降水变化特征分析[J].水资源与水工程学报,27(3):95-100.

侯保灯,吴永祥,占许珠,等,2014.中国年最大致洪暴雨落区随机性描述与预测[J].水电能源科学,32(3):1-4.

连明涛,朱文升,2014.特大暴雨递减指数的研究分析[J].水利规划与设计,6(11):14-16.

李剑锋,张强,白云岗,等,2012.新疆地区最大连续降水事件时空变化特征[J].地理学报,67(3):312-320.

任飞鹏,2016.近61年武汉市降水变化特征及趋势[J].水电能源科学,34(7):6-10.

史培军,孔锋,2016.1951－2010年中国年代际累积暴雨时空格局变化的相关因素研究[J].地理科学,36(10):1 457-1 465.

王坚红,徐碧裕,2014.华南前汛期广东暴雨分区动力特征及特大暴雨分析[J].气象与环境学报,30(6):43-51.

徐毅青,陈华,2016.台风暴雨区低频泥石流的分形特征[J].科技通报,32(4):55-58.

郑腾飞,郭建茂,尹继福,等,2012.基于DFA法的江苏省极端降水时空分布特征研究[J].自然灾害学报,21(4):76-83.

Foufpula-Georgou E,Gupta V V K,Waymire E,1984.Scaling considerations in the modeling of temporal rainfall[J].Water Resources Research,20(11):1 611-1 619.

Keden B,Chiu L S,1987.Are rain rate processes self-similar[J].Water Resources Research,23(10):1 816-1 818.

Koutsoyiannis D,Foufoula-Georgiou E,1997.A scaling model of a storm hyetograph[J].Water Resources Research,29(7):2 345-2 361.

Lovejoy S,Schertzer D,1985.Generalized scale invariance in the atmosphere and fractal models of rain[J].Water Resources Research,21(8):1 233-1 256.

Mandelbrot B B,1982.The fractal geometry of nature[M].San Francisco:Freeman.

Mandelbrot B B,Wallis J R,1969.Some long-run properties of geophysical records[J].Water Resources Research,5(2):321-340.

Menabbde M,Seed A,Pegram G,1999.A simple scaling model for extreme rainfall[J].Water Resources Research,35(1):335-339.

Michele C D,Kottegoda N T,Rosso R,et al,2001.The derivation of areal reduction faction of storm rainfall from its scaling properties[J].Water Resources Research,37(12):3 247-3 252.

Waymire E,1985.Scaling limits and self-similarity in precipitation fields[J].Water Resources Research,21(8):1 272-1 281.

Fractal characteristic analysis of extreme rainfall in Wuyi Mountain from 1990 to 2014

JI Zhi-Rong1,HE Dong-Jin2,3∗,WU Li-Yun2,YOU Wei-Bin2,CAO Yan3,CHEN Li-Qin1
(1.College of Computer and Information Sciences,Fujian Agriculture and Forestry University,Fuzhou,Fujian 35002,China；2.College of Forestry,Fujian Agriculture and Forestry University,Fuzhou,Fujian 350002,China；3.Jinshan College of Fujian Agriculture and Forestry University,Fuzhou,Fujian 35002,China)

Based on the fractal and chaos theory,the paper analyzed the time-series of extreme rainfall in Wuyi Mountain from 1990 to 2014,rebuilt the embedding space,calculated the correlative dimension and saturated embedding dimension,and determined the required number of basic variables of the correspond dynamic power system was 8.Moreover,according to the R/S analysis,the Hurst index was calculated as 0.85,which was inferred that the timeseries of extreme rainfall in Wuyi Mountain had the long-term memory characteristics.Finally,by the weighting zeroorder local-region prediction,we forecasted the short-term extreme rainfall in Wuyi Mountain.The results could reflect the fractal characteristics of extreme rainfall objectively and reasonably,and would provide the basic information for establishing the forecasting model of extreme rainfall time-series.

extreme rain； fractal method； correlative dimension； Hurst index； weighting zero-order local-region prediction

O213.9；S711

A

1001－4276－(2017)01－0118－07

纪志荣，何东进，巫丽芸，等，2017.1990－2014年武夷山特大暴雨的分形特征分析[J].武夷科学，33:118-124.

2017－04－28。

福建省教育厅项目(JA13118，JK2013016)。

纪志荣(1979－)，女，讲师，博士研究生。研究方向:统计学、森林经理。Email:15469495＠qq.com。∗

何东进(1969－)，男，教授，博士生导师。研究方向:生物统计、森林经理。Email:fjhdj＠126.com。

(责任编辑:陈晓雯)