模糊控制系统稳定性判定方法的研究
2017-12-06张立众马永翔
张立众,马永翔
(陕西理工大学 电气工程学院, 陕西 汉中 723003)
模糊控制系统稳定性判定方法的研究
张立众,马永翔
(陕西理工大学 电气工程学院, 陕西 汉中 723003)
介绍了模糊控制器稳定性判定的几种情况,来源于非线性数学模型描述的非线性控制系统的稳定性分析.其中的一些方法针对具体问题或针对严格规定的模糊控制器结构,对于非线性继电器模型来模拟的模糊控制器或MIMO控制系统可以使用奈奎斯特稳定判据确定模糊控制系统的稳定区域.对于被控系统的稳定性模糊制器的输入采用线性函数和一阶导数的情况下,使用模糊控制器的滑模运算.类似的采用滑块控制原理评价.最后说明了李雅普诺夫的稳定性原理对模糊控制的3种稳定性判定.
模糊控制;李雅普诺夫;稳定性
控制系统稳定性理论的严格数学结构某种程度上程度上模糊控制器的模糊特性相对立.但是仍然是模糊控制器设计一个关键问题.模糊主要批评与他缺乏精确的稳定性分析有关,这也是人们研究潜在技术以解决模糊控制系统稳定性问题的原因[1-2].操作员的经验是模糊控和算法基础.依据某种准则,在不知道何种行为造成系统稳定的情况下,操作员能够使系统进入预期状态,同时操作员也知道某些操作可能导致系统不稳定行为的发生.从操作员的角度看,导致被控系统不稳定行为是由语言只描述的,因此稳定区域没有严格的限定.作为模糊的设计者,应该在控制器最终结构上从分考虑这些行为的描述性理由.
1 模糊控制器稳定性的几种方法
一些技术来源来源于非线性数学模型描述的非线性控制系统的稳定性分析.其中的一些方法要么针对具体问题,要么针对严格规定的模糊控制器结构[3].例如在文献[4]中,对于一类用多值非线性继电器模型来模拟的模糊控制器,可以使用奈奎斯特稳定判据确定模糊控制系统的稳定区域.这种策略也适用MIMO控制系统.其缺点是过程传递函数必须已知的.如果考虑模糊控制的主要前提:如果系统模型的知识是不完善的或根本不存在的,那么这种方法难以实现稳定性分析.
分析模糊控制器的滑模运算可以评价稳定型.在文献[5]中,提出了一种滑块模糊控制器的设计方法,并证明了被控系统的稳定性模糊控制器的输入采用线性函数s=c×e×e′和一阶导数s′,其中e为参考输入和系统输出的偏差,由于s是用两个变量定义的,因此超平面就是s=0,则c×e=-e′.如果模糊控制器的输出是在条件永远满足的条件s×s<0下得出的则系统是稳定的,以非线性倒立摆控制问题为例结果表明这种方法是有效的,既有较大的实际价值.这种方法的优点是不需要系统模型的知识.但是他要求控制信号相对函数s×s′如何变化的定量关系.
对于类似的非线性系统,使用Taking-Sugenolex类型的变结构模糊控制器,标准输入为e和e′文献[6]已经说明利用滑块控制原理也可评价,在这种方法中,相平面被划分为九个区域,模糊规则结论部分的线性函数取决于相轨迹的位置.
类似的相平面划分办法见文献[7].首先,把相平面分成8个区域,利用李雅普诺函数,确定每个区域渐近稳定的非线性函数,然后把它作为相应模糊规则的结论部分.
文献[8]使用模糊灵敏度概念解决了稳定性评价问题.这种方法能够使系统稳定的参数变化范围.
模糊逻辑也可以用来确定模糊系统模型.基于此,文献[9-10]分别给出了模糊证明模糊过程模型稳定性的方法.这两种方法均采用Taking-Sugeno控制器李雅普诺夫函数,证明了只要规则结论部分的线性模型是稳定的,模糊模型就将是稳定.
2 李雅普诺夫的稳定性理对模糊控制的判定
在模糊控制文献中,大多数方法是基于李雅普诺夫的稳定性理论,因此根据里亚夫诺夫理论,把稳定性分为:
1)如果初始条件的微小变化引起状态轨迹的微小变化,即
∀t0,∀ε>0;∃δ>0:‖x(t0)-xe‖<δ⟹‖x(t0)-xe‖<ε,t≥t0
称平衡点xe是稳定的.
2)如果称平衡点是稳定的,且当时间t趋于无穷时,状态轨迹x(t)平衡点.即
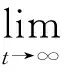
则称平衡点xe是渐近稳定的.
李雅普诺夫系统稳定形势是以观测系统的能量平衡为基础的.根据李雅普诺夫系统原理,连续能量消耗的系统最终将进入平衡状态.因此,利用某个系统能量函数能够评价系统的稳定性,这个函数通常称为李雅普诺夫函数或李亚欧诺夫候选函数.在这里要强调的是,对于所考察的系统,在找到一个能够证明系统处于稳定的恰当函数之前,可能要够构造很多函数(候选函数),并检验它们.李雅普诺夫函数连续连续和正定的.x≠0有
V(x)>0 ,

最常用的李雅普诺函数形式是广义二次型,即V(x)=xTPx,这里x是态矢量,P为正定矩阵(当P=PT时,如果P的所有特征值都是正的,那么矩阵P为正定的).由于把李亚欧诺夫函数定义为二次型形式,因此系统稳定型的问题就转换为寻找一个恰当的矩阵P的问题.
除系统变量外李雅普诺夫函数也可以是包含模糊控制器参数的其他二次型形式,在这种情况下,稳定性分析是调节综合算法的根据,即找到的保证系统稳定工程实现中难以实现.需要注意的是,在文献中长讨论有关调节算法综合的全局稳定性问题,但从实践角度看,有界输入-有界输出稳定型才是跟为重要的.
3 结 语
本文就模糊控制器的一个关键问题模糊控制系统的稳定性展开说明分析.根据李雅普诺夫稳定理论对模糊控制系统稳定性进行了讨论.
[1] FRANCHI E, MNARESI N, ROVATTI R,etal. Analog synthesis of nonliner funcitions based on fuzzy logic [J]. IEEE Journal of Solid State Ciruits, 1998, 33: 885-895.
[2] LANDOLT O. Low power analog fuzzy rule imlemention based on a linear transisteor network [C]//International Conference on Microelectronics for Neural networks, 1996.
[3] RODRIGUEZ-VAZQUEZ A, NAVAS R, DELGADO-RESTITUTO M,etal. A modular programmable COMS analog fuzzy conttroller chip [J]. Circuits and Systems II Anlaog and Digital Signal Progcessing IEEE Transactions on, 1999, 46: 251-265.
[4] FP-3000 digital Fuzzy Processor User’s Manual [R]. OMrom Corporation, 1991.
[5] PAGNI A, POLUZZI R, RIZOTTO G. Auto maticsynthesis, analysis and implementatiion of fuzy contronller [C]//IEEE International Conference on Fuzzy Syetems, 1992.
[6] HOGENER J. Fuzzy PLC: aconnection with a future [C]//The Ist European Congress on Fuzzy and Intelligent Technologies, 1993.
[7] YAMAKAWA T. A fuzzy programmable logic array (fuzzy PLA) [C]// San Diego: IEEE International Conference on Fuzzy Systems, 1992.
[8] MCKENNA T, WILANOXSKI B M. Implementing a fuzzy system on a field programmable gate array [J]. International Joint Conference on Neural Networks, 2001, 1(1): 189-194.
[9] SUGENO M. Industrial applications of fuzzy control [M]. New York: Elsevier Science Inc, 1985. 231-239.
[10] BOGDAN S, KOVACICZ, LONCAR D,etal. Fuzzy gain scheduling control of the condensate level [C]//Cd-rom Mediiterranean Conference on Control and Automation, 2001.
Researchonmethodofdeterminingstabilityoffuzzycontrolsystem
ZHANG Li-zhong, MA Yong-xiang
(School of Electrical Engineering, Shaanxi University of Technology, Hanzhong 723003, China)
This paper introduced several conditions to determine the stability of the fuzzy controller and the stability analysis of nonlinear control system source was described in the nonlinear mathematical model.Some methods to solve the concrete problems or the stucture of the fuzzy controller was strictly regulated,for the nonlinear relay model to simulate the fuzzy controller or MIMO control system can use the Nyquist stability criterion to determine the stability region of fuzzy control system for the stability of the controlled system of the fuzzy controller input usign linear function and derivative under the condition of using sliding mode fuzzy controller.Finally,the slider control similar to that Lyapunov stability principle of 3 kinds of stability of fuzzy control decision was discussed.
fuzzy control; Lyapunov; stability
2016-09-28.
陕西省教育厅项目(16JK1154)
张立众(1969-),男,硕士,讲师, 研究方向:智能控制系统.
TP273
A
1672-0946(2017)05-0575-02
