合作学习与数学建模在常微分方程教学中的应用
2017-12-05苗春梅张晓颖
苗春梅,张晓颖
(长春大学 理学院, 长春 130022)
合作学习与数学建模在常微分方程教学中的应用
苗春梅,张晓颖
(长春大学 理学院, 长春 130022)
常微分方程是高等院校数学类、信息与计算科学等专业的重要专业基础课之一。如何使学生在学习过程中掌握常微分方程的思想方法、具备以常微分方程为理论工具解决实际问题的能力,是常微分方程教学与改革中必须要解决的问题。本文结合常微分方程课程的特质,探讨合作学习模式与数学建模思想融入其教学过程的机理与方式,培养学生研究学习与创造学习的思维与能力。
常微分方程;合作学习;数学建模思想;教学改革
“高等教育面向21世纪教学内容和课程体系改革计划”的目标是培养具有以创新精神和实践能力为核心的综合素质的高级人才。具有创新精神和实践能力的人才必须掌握现代科学技术研究的方法和数学技术,而数学技术主要由数学分析技术、数学建模技术、数学软件技术、数学实验技术等组成[1]。
常微分方程源于对物体运动过程的数学研究,是一门应用性很强的学科,在物理、生物、机械工程等领域都有着广泛的应用。比如,导弹弹道计算与飞机飞行中的稳定性研究,生物种群稳定性的研究等都归为常微分方程模型[2]。就信息与计算科学专业而言,“常微分方程”是“数学分析”、“高等代数”和“解析几何”的后继课程,又是“数学建模”、“数值分析”等课程的先修课程,是从理论向应用过渡的纽带课程。因此,如何在常微分方程课程的教学中突出其应用性与数学模型的思想,是其教学亟待解决的重要问题。长期以来,以理论推导与计算为主导的教学模式消解了常微分方程的实践性,以至学生对其应用性缺乏认识。
基于此,本文提出“合作学习模式”与“数学建模思想”相结合的教学模式,引入开放性题,让学生通过合作学习模式、应用数学建模思想解决问题,培养学生的创新能力、合作能力与研究能力。
1 合作学习与数学建模
1.1 合作学习模式
合作学习兴起于20世纪70年代的美国,经过30多年的理论研究和实践发展,合作学习已成为世界上许多国家普遍采用的教学理论与实践策略,被认为是“当代教育理论、研究和实践中影响最大和成果最多的领域之一”。
不同的学者对合作学习的有着各具特色的研究与推进。美国约翰霍布金斯大学的Slavin提出了“学生小组成就区分法”,“合作学习是指使学生在小组中从事学习活动,并依据他们整个小组的成绩获取奖励或认可的课堂教学技术”[3]。美国明尼苏达大学的约翰逊兄弟认为:“合作学习就是在教学中运用小组,使学生共同活动以最大程度地促进他们自己以及他人的学习。”[4]
20世纪80年代末、90年代初,我国学者开始关注合作学习的研究与应用。王坦认为:“合作学习是一种旨在促进学生在异质小组中互相合作,达到共同的学习目标,并以小组的总体成绩为奖励依据的教学策略体系。”[5]黄政杰认为:“合作学习是学生一起工作达成其共同的目标,此目标不但有利于己,也有利于其他人。合作学习采取小组学习方式,学生一起学习进而扩大自己和他人的学习。在合作学习中,所有成员式相互得力的,你的成功也就是我的成功,我的失败也正是你的失败,这是一种命运共同体的状态,是属于积极互赖的情景。”[6]
合作学习的课堂实施是合作学习理论在课堂教学中的应用与实践,但是国内大部分的合作学习的课堂案例都是中小学课程教学,缺乏在大学课堂教学中的优秀案例。
1.2 合作学习与数学建模活动的关系
数学建模于20世纪六七十年代进入西方国家的大学,80年代初开始进入我国大学。数学建模活动是培养学生自学能力、合作能力、研究能力和创新能力的有效途径,近年来受到数学教育者的广泛关注。
合作学习,即“学生在小组中从事学习活动,并以他们小组的表现为依据获得奖励或认可的课堂教学技术”。在数学建模竞赛活动中,合作学习主要体现在教师与学生的合作学习、学生与学生的合作学习两个方面,即在教师的指导下,学生以小组为单位进行学习。因此,合作学习是数学建模活动重要的组织模式。
2 设置常微方程开放性题目
在常微分方程教材中,习题基本上是为了使学生理解和掌握数学结论而设计的。在这种情况下,学生在学习过程中往往容易产生以死记硬背代替主动参与、以机械方法代替智力活动的倾向。要改变这种情况,使学生的学习更多地体现以学生为主体的积极探究精神,适当增加开放题,让学生以合作学习的方式,应用数学建模的思想解决问题是必要的。
2.1 开放题的设置原则
(1)问题导出理论、理论深化问题。常微分方程课程教学的开放题设置要与教材内容有机结合起来,而不是做成各自独立的两套系统。比如在讲授一阶和二阶常微分方程内容时,设置相关的应用性开放题,使学生了解问题背景,能够学以致用。另一方面,开放题的设置应与微分方程发展的主流相结合,使学生了解前沿问题的研究进展。这要求教师要对微分方程、动力系统和非线性科学领域的主流问题有所研究,从而渗透到起奠基性作用的常微分方程课程的教学中。
(2)针对实际能力、引导探索兴趣。地方高等院校是一个基础和能力有较大差异的学生群体,大约可以分成三类:A类,基础和能力较强;B类,基础和能力一般;C类,基础和能力相对较弱。因此,常微分方程课程教学中开放题的设置,也要根据学生的能力和水平分层设置,不能“一刀切”。
2.2 开放题的解决方法
学生要以小组的形式进行合作学习,结合数学建模的思想,在老师的指导下解决问题。以下根据笔者的研究方向,选取常微分方程课程教学中的开放题,通过指导学生解决这两类问题的过程,阐释课程教学中开放题的解决方法。
(1)生物种群模型。生物种群模型的稳定性问题是笔者一直研究的课题,在常微分方程课程教学中引入相关的生物模型作为开放题,能够使学生更好地掌握一阶常微分方程理论、应用和前景。Logistic模型[7]
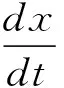
(2.1)
是一阶非线性常微分方程,是生物学中最简单的单种群模型,最早由比利时数学家Verhulst于1838年提出的描述种群增长过程的数学模型。1920年,美国人口学家Pearhe和Reed在研究美国人口问题时再次提出这个方程,称之为Verhulst-pearl阻滞方程,后来被称为Logistic模型。学生学习了一阶常微分方程的基本理论之后能够求解该方程。
首先,对学生进行分组。共7个人:3个A类学生,2个B类学生,2个C类学生。其次,提出问题,建立模型。由2个B类学生查阅资料,分析数据,建模。然后,解决问题。由2个C类学生根据所学的一阶常微分方程理论求解。最后,分析问题。由3个A类学生做如下几方面的工作:① 结合模型的建立和求解,分析问题,并提出修改和推广建议。② 在老师的指导下,查阅该问题的研究进展和发展前景。③ 撰写成文。
(2)振动问题。1831年,英国曼彻斯特的布劳顿桥上一队士兵齐步通过的时候桥突然坍塌。1940年,美国华盛顿塔克马大桥突然发生振动,振幅达到28英尺。振动是工程中常见现象,研究振动规律有着极其重要的意义。近些年,笔者关注经典的振动方程
mx″+kx′+hx=f(x).
(2.2)
的研究。根据我们的研究成果,在常微分方程课程教学中引入经典的振动方程(2.2)作为二阶常微分方程理论的开放题,以使学生更好地掌握二阶常微分方程理论、应用和前景。对学生进行分组解决开放问题(2.2)的过程和方法同问题(2.1).
3 结语
在常微分方程课程的教学中,通过设置诸如以上的应用性问题作为开放题目,组织学生分组合作进行研讨,提出建模的基本思路,然后教师结合常微分方程的思想方法与学生进行深入研讨,推进问题的解决。在这样的学习过程中,一方面,教师能够结合具体问题很好地具体向学生解释常微分方程的基本理论,形成学生对常微分方程的系统认识与逻辑把握;另一方面,学生在互动中真正体会到合作的意义,在争议与碰撞中表现了自己的创造性思考与团队意识,形成了创新思考的内在动力和修正思想的自觉意识。同时,设置开放题应该注意以下两个问题:一是避免流于形式,问题不要过大,要注重精细;二是教师要对开放题有一定的研究。
[1] 石永福,王立群. 现代数学技术及其影响 [J]. 西北师范大学学报(自然科学版),2005(2):94-97.
[2] JI.C.庞特里亚金.常微分方程 [M].林武忠,倪明康,译.北京:高等教育出版社,2006.
[3] M.C. Wittrock. The cognitive movement in instruction [M]. Educational Psychology, 1978(71):60-66.
[4] 大卫.W. 约翰逊,罗格.T. 约翰逊,卡尔. A.史密斯.合作学习的原理与技巧:在教与学中组建有效的团队[M].刘春红,译.北京:机械工业出版社,2002.
[5] 王坦. 合作学习导论 [M]. 北京:教育科学出版社,1994.
[6] 黄政杰,林佩璇. 合作学习 [M].台北:五南出版社,1996.
[7] 余爱华. Logistic模型的研究 [D]. 南京:南京林业大学,2003.
责任编辑:刘 琳
ApplicationofCooperativeLearningandMathematicalModelinginOrdinaryDifferentialEquationTeaching
MIAO Chunmei, ZHANG Xiaoying
(College of Science, Changchun University, Changchun 130022, China)
Ordinary differential equation is one of the important professional basic courses in mathematics as well as informational and calculative science in universities. It is a fundamental problem in teaching and reform to make students get the thinking methods of the ordinary differential equations and have the ability to solve practical problems by using ordinary differential equalities as theoretical tools. This paper, combining with the characteristics of ordinary differential equation course, discusses the mechanism and way of integrating the thought of cooperative learning and mathematical modeling into ordinary differential equation teaching, trying to cultivate the thinking and ability of students’ research learning and creative learning.
ordinary differential equation; cooperative learning; mathematical modeling thought; teaching reform
2017-04-06
吉林省教育科学规划课题(GH170133);吉林省高等教育学会2017年度高教科研课题(JGJX2017B28)
苗春梅(1977-),女,辽宁大连人,副教授,博士,主要从事常微分方程理论研究。
G642
A
1009-3907(2017)10-0088-03
