基于正交试验的隧道开挖面位移释放分析

苏永华，孙旺，方砚兵

(湖南大学 土木工程学院，湖南 长沙 410082)

基于正交试验的隧道开挖面位移释放分析

苏永华†，孙旺，方砚兵

(湖南大学 土木工程学院，湖南 长沙 410082)

针对目前关于位移释放系数的计算方法比较复杂的问题，基于二次回归正交组合试验设计方法，提出了位移释放系数公式构建方法，应用该方法对静水应力场中圆形隧道进行了一系列数值试验，建立了考虑多个因素的开挖面位移释放系数拟合公式，比较了各影响因素的敏感性大小.通过数值算例和工程实例分析，初步验证了该方法的有效性.研究结果表明：对于不同级别岩体，同一因素对开挖面位移释放系数的影响程度不一；地应力水平、岩体扰动、地质强度指标、H-B常数和泊松比对开挖面位移释放系数的影响较大，而岩石单轴抗压强度和变形模量影响较小.

位移释放系数；纵向变形曲线；正交设计；回归分析

在应用收敛-约束法进行隧道支护结构设计时，确定支护设置时隧道洞壁已经产生的前期位移量，对支护结构的设计至关重要.前期位移量可通过位移释放系数得到.位移释放系数即为某一时刻隧道某处的位移量与该处能达到的最大位移量的比值.在隧道工程中，沿隧道纵向(轴线方向)洞壁各点位移释放系数与到开挖面的距离的关系曲线称为纵向变形曲线(Longitudinal Displacement Profiles,LDP).

由于隧道开挖面附近呈现复杂的三维力学性态，理论分析困难，故目前关于隧道前期位移量与位移释放系数的研究多是通过现场实测和数值模拟进行.Carranza-Torres等[1]和李煜舲等[2-3]根据现场监测资料，提出了关于LDP的拟合公式；周建春等[4]考虑时间效应，采用BP神经网络算法对隧道围岩变形监测数据进行了拟合；方勇等[5]通过室内模型试验对上下台阶法隧道和单侧壁导坑法隧道的拱顶位移进行了对比分析.数值模拟方面，Unlu等[6]给出了弹性条件下开挖面位移释放系数与泊松比的关系式；Panet[7]、李煜舲等[8]基于三维弹性有限元分析给出了LDP拟合公式；Vlachopoulos等[9]考虑塑性区范围的影响，采用三维有限差分法得出了LDP拟合公式；张平等[10]给出针对城门形隧洞上下台阶开挖工况的LDP拟合公式；吴顺川等[11]提出了基于岩体基本质量指标(BQ)的LDP拟合公式.然而上述研究中，根据特定工程监测资料得出的结论难以适用于其他情况；基于数值模拟得出的拟合公式不是考虑因素太少就是过于复杂，限制了该类方法的使用.因此，应充分考虑各个因素的影响，建立一个较简单的位移释放系数公式，以适应工程需要.

本文针对开挖面位移释放系数，基于二次回归正交试验设计，提出了位移释放系数公式构建方法，以静水应力场下的圆形隧道为例详细说明了该方法的应用过程.利用数值模拟技术，考虑多个因素的影响，探讨了各因素对开挖面位移释放系数的影响程度，得到了位移释放系数的回归方程，通过数值算例和工程实例分析，初步验证了该方程的准确性.

1 纵向变形曲线与位移释放系数

(1)

图1 LDP示意图Fig.1 Longitudinal displacement profiles

2 基于回归正交的位移释放分析

回归正交组合试验设计是将正交设计和回归分析结合起来的一种试验设计方法，它能在因素的试验范围内选择适当的试验点，用较少的试验建立起一个精度高、统计性质好的回归方程，还能够解决试验优化问题.

2.1 位移释放系数公式构建方法

本文给出一种基于二次回归正交组合设计的位移释放系数公式构建方法，设计者可根据实际情况改变围岩参数范围、隧道洞形、开挖方式、应力类型等条件，得到更具针对性的、更加精确的位移释放系数公式.具体步骤如下：

1)确定开挖面位移释放的影响因素；

2)建立数值模型；

3)因素水平编码：确定各影响因素的变化范围和零水平试验次数，对因素水平进行编码，得到规范变量；

4)确定试验方案：根据因素数选择合适的正交表，确定二水平试验方案，将二次项中心化处理，得到具有正交性的二次回归正交组合设计方案；

5)试验方案实施；

6)回归方程的建立和显著性分析，确定各影响因素敏感性大小，得出关于开挖面位移释放系数的回归方程.

2.2 开挖面位移释放影响因素

基于广义Hoek-Brown准则，对该准则中各个参数对位移释放系数的影响进行分析.

Hoek-Brown准则由E. Hoek和E. T. Brown于1980年首次提出，经多次补充与改进，已成为现今影响最大、应用最广的岩石强度准则.它反映了岩体的非线性破坏特征，以及岩石强度、结构面、应力状态对岩体强度的影响，而且弥补了Mohr-Coulomb强度准则的不足，能够解释低应力区、拉应力区和最小主应力对岩体强度的影响，并适用于破碎岩体和各向异性岩体[12].其表达式为

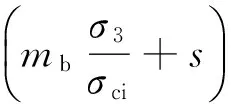
(2)

式中：σ1和σ3分别为岩体的最大和最小有效主应力；σci为完整岩石的单轴抗压强度；mb，s，a为反映岩体破碎程度和节理特征的常数，由式(3)确定.

(3)

式中：mi为反映岩石软硬程度的H-B常数，取值范围为0.001～25；GSI为地质强度指标(Geological Strength Index)；D为考虑爆破破坏和应力释放对节理岩体扰动程度的岩体扰动参数，取值从非扰动岩体的D=0到扰动性很强岩体的D=1.

在工程实际中，不仅要对上述参数做一个估计，还要对岩体的整体质量行为做一个判断，为此E. Hoek和E. T. Brown引入岩体整体强度σcm的概念，具体表达式如下：

(4)

考虑3个方面7个因素及其相互作用对开挖面位移释放的影响.1)岩石基本参数：泊松比υ、变形模量Em、单轴抗压强度σci；2)Hoek-Brown准则参数：mi，GSI，D；3)应力水平：以初始应力σ0与岩体整体强度σcm的比值σ0/σcm表示.

为保证所选取岩体参数的代表性，以Hoek等[13]根据大量工程实践总结得到的典型岩体参数为基础进行分析，具体数值见表1.根据表1将岩体分为poor-average(P-A)和average-good(A-G)两个级别，并以P-A级别岩体为例详细说明位移释放系数公式构建方法的应用过程.

表1 典型岩体参数

2.3 数值模型建立

数值试验采用有限差分软件FLAC3D进行计算.假设一处于静水应力场的圆形无支护隧道，岩体均质且各项同性，隧道开挖不考虑地下水及时间的影响.隧道半径R=6 m，采用全段面开挖，进尺为1 m，模拟范围径向取6倍半径，纵向取20倍半径.由于几何形状与边界条件的对称性，取1/4模型进行计算.模型尺寸及边界条件如图2所示.

图2 模型尺寸及边界条件Fig.2 Geometry and boundary conditions of the model

2.4 因素水平编码

分别以表1中一般岩体和差岩体的参数作为各参数的上下限，σ0/σcm取值范围从1～5，D取值范围从0～1.各因素水平编码见表2.

2.5 二次回归正交组合试验方案

选用正交表L16(215)，二水平试验次数为16，星号试验次数为14，零水平试验次数为1，总试验次数为31.将Z1～Z7分别置于正交表的第1，2，4，8，11，13，14列，将交互作用Z4Z5，Z4Z6，Z5Z6，Z3Z6，Z3Z7，Z3Z4，Z3Z5分别置于第3，5，6，9，10，12，15列，第7列空白.该试验方案的回归方程为：

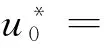
b46Z4Z6+b56Z5Z6+b36Z3Z6+

b37Z3Z7+b34Z3Z4

(5)

式(5)有21项未知系数，小于试验次数，试验方案可行.二次回归正交组合试验方案见表3.

表2 因素水平编码

表3 试验方案及结果

2.6 试验方案实施

根据试验方案进行数值试验，试验结果见表3.

2.7 回归方程及显著性分析

按照表3的试验方案和结果整理分析可得到式(5)各项系数.对试验结果进行回归分析，各因素的相应统计量见表4，表中F′为剔除不显著项后该因素的F统计量.

对于因素A，若FA>F0.01(dfA,dfe)，就认为因素A对试验结果有非常显著的影响；若F0.05(dfA,dfe)

表4 各因素F统计量

注：F0.05(1,9)=5.12，F0.01(1,9)=10.56，F0.01(1,22)=7.95.

由表4可知，Z1,Z2,Z3,Z3Z6,Z3Z7,Z3Z4,Z3Z5,Z1',Z2',Z3',Z4',Z5',Z6'对结果的影响不显著，将其计入残差，重新计算各因素的F统计量.剔除不显著项后的回归方程F统计量为FR=76.15，相应的判别值为F0.01(8,22)=3.45，FR>F0.01(8,22)，回归方程仍是显著的，回归方程为：

(6)

将自然变量回代到式(6)，得到：

5.28D+0.24GSI·(σ0/σcm)+1.06GSI·D-

8.10(σ0/σcm)·D-27.75D2

(7)

由上述分析可知，在P-A级别内，影响开挖面位移释放系数的7个因素中，参数敏感性由大到小依次为：(σ0/σcm),D,GSI,mi,v,σci,Em.其中，v,σci和Em的影响很小，计算时可不考虑.

2.8 A-G级别岩体

应用2.1节中所述的位移释放系数构建方法，可得到A-G级别岩体开挖面位移释放系数的回归公式：

12.22D+0.05GSI·(σ0/σcm)+0.26GSI·D-

1.31(σ0/σcm)·D-0.22(σ0/σcm)2

(8)

与P-A级别岩体不同，在A-G级别岩体范围内，泊松比成为影响开挖面位移释放系数的最显著因素，各参数对开挖面位移释放系数影响程度由大到小依次为：v，(σ0/σcm)，mi，D，GSI，Em，σci；其中Em，σci的影响不显著.

2.9 变形模量的影响

一般认为，围岩的变形模量对隧道洞壁变形有重要影响.然而，从以上分析可以看到，无论对于哪种级别的岩体，变形模量的变化对开挖面位移释放系数的影响很小以至于在计算时可以忽略.为进一步研究其中的机理，应用控制变量法对变形模量的影响进行研究.

以表1中一般岩体为基础，控制其他变量保持不变，对不同大小变形模量的岩体进行模拟，结果见图3.图3(a)为一般形式的LDP曲线，图3(b)为归一化LDP曲线，图中ur/ur,max即位移释放系数.

(a)一般形式的LDP曲线

(b)归一化LDP曲线图3 变形模量对纵向变形曲线的影响Fig.3 Effect of Em on LDP

从图3(a)可以看到，隧道各处收敛位移和最大位移都随变形模量的增大而减小，正是这种同比例的增减，导致洞壁位移与最大位移的比值即位移释放系数随变形模量的变化而保持不变，如图3(b)所示，不同变形模量岩体的归一化LDP曲线几乎重合.

3 数值算例

数值算例中岩体的参数见表5，其中岩体A，B，C，D来源于文献[13]和[14]中的实际工程.取地应力水平σ0/σcm=3.5，岩体扰动参数D=0.7.数值模拟结果见表5.

由于一般岩体既属于P-A级别岩体也属于A-G级别岩体，C岩体多数参数在A-G级别岩体范围内而个别参数在P-A级别岩体范围，故对这两种岩体从式(7)和式(8)两方面进行了检验.

由表5可知，式(7)和式(8)具有较高的准确性.针对C岩体的比较分析可知，当岩体的参数不能完全归入某一级别时，需对该岩体进行判断，若总体上属于质量较差的岩体则采用式(7)进行计算，反之则应采用式(8)进行计算.C岩体总体上质量较好，采用式(7)所得结果的误差远小于采用式(8)的误差.

表5 数值算例岩体参数及数值模拟结果

4 实例分析

纵向变形曲线和位移释放系数是收敛-约束法的重要组成部分.通过位移释放系数公式可求得隧道开挖后开挖面处洞壁收敛位移，即支护特征曲线的起点，结合围岩收敛曲线，由收敛-约束原理得到支护结构的稳定性系数，从而对支护结构的稳定性进行定量评价.苏永华等[15]通过案例分析详述了位移释放系数在地下结构稳定性分析中的应用.

4.1 工程简介

湖南湘西某公路隧道全长约3.4 km，最大埋深约700 m，隧道轴向为南北方向，断面型式为马蹄形，高度为8.6 m，跨度为11.6 m.

按隧道洞身所处地质环境，可分为南北两段.北段岩层岩性主要为粗砂质、结构致密的中厚至厚层状页岩，层间结合良好，无地下水.南段主要为泥质细砂岩，岩体节理裂隙发育，涌水量达每小时20 m3.岩体参数见表6.

根据Bienawski提出的岩体分类RMR法，北段隧道围岩RMR=55，属于质量良好的岩体；南段隧道围岩RMR=39，属于质量差的岩体.根据Barton等人提出的岩体分类Q法，北段隧道围岩Q=10.74，属于质量好的岩体；南段隧道围岩Q=0.78，属于质量很差的岩体.综合围岩参数的分布情况、RMR法和Q法，将北段隧道围岩归为A-G级别岩体，南段围岩归为P-A级别岩体.

表6 围岩基本参数

根据南北段隧道不同的地质条件，北段采用锚喷支护结构，南段采用锚杆+喷射混凝土+钢拱架支护结构.支护结构的计算采用Carranza-Torres等[1]的建议，将支护结构的总刚度视作各单元刚度之和.北段支护结构总刚度为65.850 4 MPa/m，允许极限变形为4.003 mm，极限抗力为0.263 MPa；南段支护结构总刚度为86.178 6 MPa/m，允许极限变形为4.003 mm，极限抗力为0.345 MPa.

隧道按新奥法组织施工，采用光面爆破，开挖后立即进行支护.北段爆破效果良好，岩体扰动参数D=0；南段爆破效果差，岩体扰动参数D=1.

4.2 围岩收敛曲线和支护特征曲线

(a)北段

(b)南段图4 隧道收敛-约束图(局部)Fig.4 Convergence-confinement curves

4.3 支护结构的稳定性系数

图4(a)中，北段围岩收敛曲线和支护特征曲线交点处p=0.178 MPa，由收敛-约束原理可知隧道北段支护结构的稳定性系数Fs=1.48.图4(b)中，南段围岩收敛曲线和支护特征曲线无交点，故隧道南段支护结构的稳定性系数Fs<1.

4.4 隧道支护结构稳定情况

该隧道于2010年初建成通车，根据监测资料，隧道北段自通车至今，支护结构表面素混凝土衬砌没有变形和裂纹，稳定状况良好.对于隧道南段某些区域，素混凝土衬砌浇筑后不久即出现环向裂纹，当时进行了修补，然而裂纹不断出现并持续发展，形成宏观裂缝.通车3个月后，支护结构破坏，隧道被迫封闭，重新支护.

隧道北段支护结构稳定性系数Fs=1.48，结构一直稳定.南段支护结构稳定性系数Fs<1，该段部分支护结构破坏，需重新支护.初步验证了式(7)、式(8)在工程应用中的有效性.

5 结 论

本文在二次回归正交组合设计方法的基础上，以开挖面位移释放系数为对象进行了一系列数值试验，得到以下主要结论：

1)给出了一种位移释放系数公式构建方法，运用该方法对静水应力场下的圆形隧道进行研究，得到了考虑多个因素的开挖面位移释放系数公式.

2)对于不同级别岩体，同一因素对开挖面位移释放的影响程度不一.总体而言，地应力水平、岩体扰动、地质强度指标、H-B常数和泊松比影响较大，而岩石单轴抗压强度和变形模量影响较小.

3)通过工程实例分析，展示了位移释放系数公式在支护结构稳定性分析中的应用过程，初步验证了公式的有效性.

4)本文主要针对全断面开挖隧道进行分析，对于采用其他开挖方法施工的情况，需进一步深入研究.

[1] CARRANZA-TORRES C,FAIRHURST C. Application of the convergence-confinement method of tunnel design to rock masses that satisfy the hoek-brown failure criterion[J]. Tunnelling & Underground Space Technology,2000,15(2):187-213.

[2] 李煜舲,林铭益. 台灣東部鐵路單軌隧道開挖支撐互制行為之探討[J]. 岩石力学与工程学报,2004,23(S2):4823-4832.

LEE Yulin,LIN Mingyi. Analysis of interaction of rock masses and support system of monorail tunnel in east Taiwan[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(S2):4823-4832.(In Chinese)

[3] 李煜舲,许文贵,林铭益. 以隧道变形量测资料分析掘进效应与约束损失[J]. 岩石力学与工程学报,2009,28(1):39-46.

LEE Yulin,HSU Wenkuei,LIN Mingyi. Analysis of advancing effect and confinement loss by using deformation measurements in tunnel[J]. Chinese Journal of Rock Mechanics and Engineering,2009,28(1):39-46. (In Chinese)

[4] 周建春,魏琴. 公路隧道围岩变形时程曲线拟合的BP算法[J]. 湖南大学学报:自然科学版,2002,29(4):79-84.

ZHOU Jianchun,WEI Qin. Study on fitting of surrounding rock deformation time-history curve by BP neural network algorithm[J]. Journal of Hunan University :Natural Sciences,2002,29(4):79-84.(In Chinese)

[5] 方勇,周超月,刘书斌,等. 上覆薄煤层采空区公路隧道开挖稳定性试验研究[J]. 湖南大学学报:自然科学版,2015,42(7):100-107.

FANG Yong,ZHOU Chaoyue,LIU Shubin,etal. Model test of excavation stability for highway tunnel beneath mined-out thin coal seam[J]. Journal of Hunan University :Natural Sciences,2015,42(7):100-107.(In Chinese)

[6] UNLU T,GERCEK H. Effect of poisson's ratio on the normalized radial displacements occurring around the face of a circular tunnel[J]. Tunnelling & Underground Space Technology,2003,18(5):547-553.

[7] PANET M. Understanding deformations in tunnels[M]//HUDSON J A,BROWN E T,FAIRHURST C,etal. Comprehensive rock engineering. Pergamon:Oxford,1993: 663-690.

[8] 李煜舲,林铭益,许文贵. 三维有限元分析隧道开挖收敛损失与纵剖面变形曲线关系研究[J]. 岩石力学与工程学报,2008,27(2):258-265.

LEE Yulin,LIN Mingyi,HSU Wenkuei. Study on relationship between convergence loss and longitudinal deformation curve in tunnel excavation by using three-dimensional finite element analysis[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(2):258-265.(In Chinese)

[9] VLACHOPOULOS N,DIEDERICHS M S. Improved longitudinal displacement profiles for convergence confinement analysis of deep tunnels[J]. Rock Mechanics & Rock Engineering,2009,42(42):131-146.

[10] 张平,尹建军,曹文贵. 上下台阶开挖下城门形隧洞纵向变形规律分析[J]. 水文地质工程地质,2009,36(2):40-46.

ZHANG Ping,YIN Jianjun,CAO Wengui. Analysis of longitudinal deformation profile in city-gate shaped tunnel using top heading and bench excavation method[J]. Hydrogeology & Engineering Geology,2009,36(2):40-46.(In Chinese)

[11] 吴顺川,耿晓杰,高永涛,等. 基于广义Hoek-Brown准则的隧道纵向变形曲线研究[J]. 岩土力学,2015,36(4):946-953.

WU Shunchuan,GENG Xiaojie,GAO Yongtao,etal. A study of the longitudinal deformation of tunnels based on the generalized Hoek-Brown failure criterion[J]. Rock and Soil Mechanics,2015,36(4):946-953.(In Chinese)

[12] HOEK E,CARRANZA-TORRES C,CORKUM B. Hoek-Brown failure criterion-2002 edition[C]// Proceedings of the North American Rock Mechanics Society NARMS-TAC 2002. Toronto: University of Toronto Press,2002: 267-273.

[13] HOEK E,BROWN E T. Practical estimates of rock mass strength[J]. International Journal of Rock Mechanics & Mining Sciences,1997,34(8):1165-1186.

[14] GUROCAK Z. Analyses of stability and support design for a diversion tunnel at the Kapikaya dam site,Turkey[J]. Bulletin of Engineering Geology & the Environment,2011,70(1):41-52.

[15] 苏永华,付雄,肖旺. 围岩收敛曲线形态对地下结构稳定系数影响分析[J]. 湖南大学学报:自然科学版,2015,42(7):87-92.

SU Yonghua,FU Xiong,XIAO Wang. The analysis for stability coefficient of underground structure with the shapes of ground response curves[J]. Journal of Hunan University:Natural Sciences,2015,42(7):87-92.(In Chinese)

Analysis on Displacement Release of Tunnel Face Based on Orthogonal Tests

SU Yonghua†,SUN Wang,FANG Yanbing

(College of Civil Engineering,Hunan University,Changsha 410082,China)

The existing computational methods of displacement release coefficient are too complex. Based on quadratic regression orthogonal design，a construction method of displacement release coefficient formula was given，and a series of numerical experiments of a circular tunnel in hydrostatic stress field were carried out by the above method. The regression equation of displacement release coefficient was established，and the sensitivity of parameters was determined. Through analysis of numerical examples and a case history，the equation was proved to be reasonable and effective. The results indicate that for different levels of surrounding rock，the effect of the same factor on the displacement release coefficient of the tunnel face is different. Stress level，disturbance of rock mass，GSI，H-B material constant and Poisson's ratio have a great influence on the displacement release of tunnel face，while the intact rock strength and deformation modulus have little influence.

displacement release coefficient; longitudinal displacement profiles; orthogonal design; regression analysis

TU458

A

1674-2974(2017)11-0156-08

10.16339/j.cnki.hdxbzkb.2017.11.018

2016-10-22

国家自然科学基金资助项目(51578232，51378195), National Natural Science Foundation of China(51578232，51378195)

苏永华(1966—)，男，湖南涟源人，湖南大学教授，博士生导师

†通讯联系人，Email：yong_su1965@126.com