基于浮框式测力模型的桥梁涡激力特性研究

牛华伟,吴润泽,陈谨林,陈政清

(湖南大学 风工程与桥梁工程湖南省重点实验室，湖南 长沙 410082)

基于浮框式测力模型的桥梁涡激力特性研究

牛华伟†,吴润泽,陈谨林,陈政清

(湖南大学 风工程与桥梁工程湖南省重点实验室，湖南 长沙 410082)

基于开发的内置浮框式三节段测力模型装置，通过弹性悬挂测振风洞试验测试了某大跨度斜拉桥初步设计主梁断面的涡振响应及对应的涡激力.分析了发生竖向涡激共振的0°与+3°两种风攻角下的数据，验证了内置浮框式三节段测力模型在桥梁断面气动力测试中的可靠性，对比研究了不同风攻角下涡激力与涡激振动响应的测试结果，探讨了锁定区间范围内涡振频率、力与位移之间相位差及涡激力做功的变化情况.结果表明，内置浮框式三节段测力模型可以在风致振动过程中同步测试气动力；所测试得到的涡激力频率在风速锁定区间内与位移响应频率完全一致，同时，模型的竖弯涡激力与涡激振动位移响应之间存在的相位差随风速增大而增大，而涡激力做功有一个先增大后减小的变化过程.

桥梁；涡激共振；涡激力；测力模型；三节段模型

桥梁主梁涡激振动是一种具有自激和强迫双重特性的风致限幅振动.工程实践表明，大跨度桥梁由于自身质量轻、阻尼低、柔度大等特性，发生涡激共振的现象时有发生，如丹麦的大带东桥[1]，中国的西堠门大桥[2]以及日本的东京湾大桥[3]等等.尽管涡激共振的限幅特性使得桥梁结构振动不会发散而导致结构毁坏，但由于其起振风速较低，风致振幅较大，长时间的振动容易引起主梁局部结构的疲劳破坏，过大的振幅也会影响行人舒适度和行车安全，因而研究涡激共振发生机理从而控制涡振振幅具有非常重要的意义.

桥梁主梁涡激振动机理的研究通常包括数值模拟和风洞试验两种方法.随着计算流体力学的迅猛发展，采用数值计算方法进行的涡振研究已经取得了很大进展[4]，但由于主梁涡振对于外形非常敏感，对计算网格精度要求很高，数值模拟仍然存在它的限制性.

节段模型风洞试验是已被证实的研究大跨度桥梁主梁涡激振动的有效途径之一.通过风洞测力测振试验，能够得到风速锁定区间内的涡激力与位移响应，根据涡激力的做功情况可以判断涡振起振消振的原因.现有风洞试验建立的半经验涡激力模型(诸如简谐力模型[5]、尾流振子模型[6-7]、经验线性模型[8]、经验非线性模型[9]以及广义经验非线性模型[10]等)可以尽可能准确地描述结构的涡激共振现象，但这并不能说明涡激力和涡激力模型的合理性.要想验证数学模型描述的涡激力是否合理，仍需要通过测定结构实际所受到的涡激力进行检验.由于测试设备的限制，通过力传感器测试得到的精度一直都不高.针对这种不足，本文希望能开发一种可以同时考虑振动响应及对应气动力的内置浮框式测力段的节段模型，以期望采用该装置在测振的同时同步得到对应的气动力，以便研究气动力与风致响应之间的相互作用.本课题组前期基于同类装置对矩形断面进行了涡激力的测试与研究[11]，证明了该装置在矩形断面上涡激力测试的有效性.本文进一步改进了该测试模型与分析方法，并利用该模型装置测试实际桥梁断面的涡激力特性，一方面希望揭示涡激共振过程中涡激力和涡激振动响应之间的相互作用，另一方面为采用该装置进一步研究自激力和抖振力特性奠定基础.

1 试验装置与涡激力识别

1.1 内置浮框式三节段测力模型

内置浮框式三节段模型由中间悬浮测力段(长度1 000 mm)和两侧补偿段(长度270 mm)组成，如图1所示.

图1 测力测振三节段模型Fig.1 Dynamometric three-segment model

补偿段与悬浮段之间采用弹性好、柔度大的防水生料布封住缝隙，保证悬浮段荷载不能通过该缝隙部位向补偿段传递.中间悬浮测力段由悬浮框支承轻质外衣，并通过7个力传感器与内支撑框相连，传感器端部设置轴向刚度远大于侧弯刚度的消扰构件，以保证单个传感器部位主要传递轴向力荷载，传感器布置方式如图2所示，其中轴向、侧向及竖向布置的力传感器分别标示Zi，Li和Vi.测力计选用德国HBM公司U9B型单向力传感器(量程200 N，桥压5 V，灵敏度1 mV/V)，如图3所示.模型内置框架部分可以重复使用，通过改变补偿段及测力段外衣形状来满足不同试验目的与要求.

1.2 涡激力识别方法

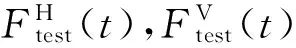
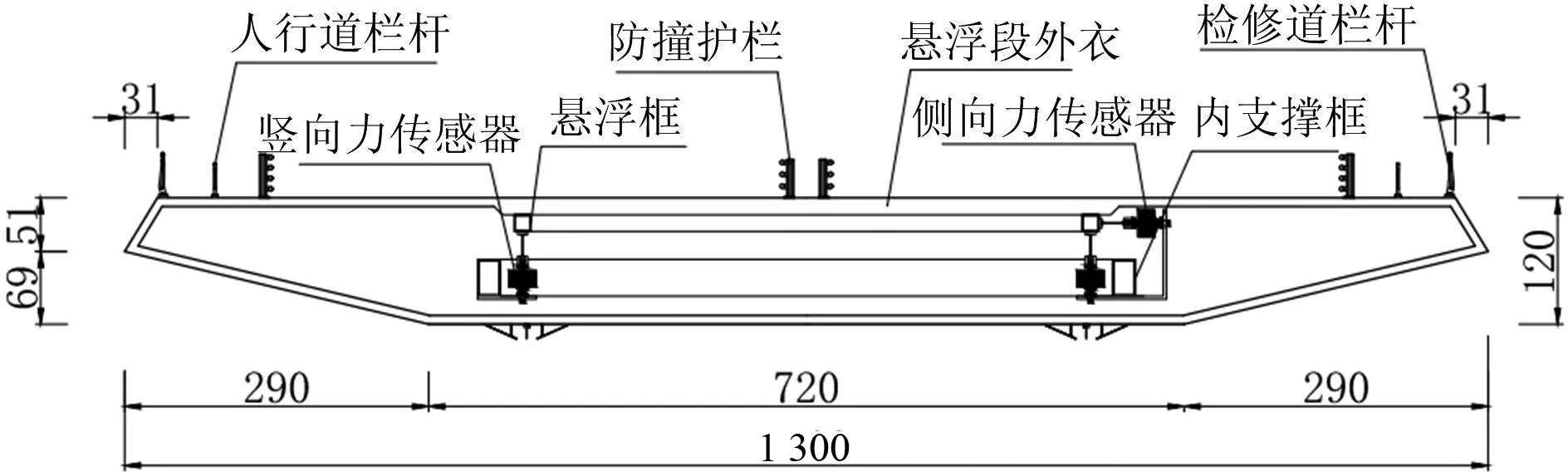
(a)传感器布置横断面图(单位：mm)

(b)三向力传感器分布图图2 力传感器布置图Fig.2 Arrangement diagram of dynamometers

图3 U9B型单向力传感器Fig.3 Shape of used U9B force sensor

图4 节段模型悬浮段外衣受力图Fig.4 Diagram of the forces on dynamometric segment coat

根据作用力的性质，气动力可分为平均分量和脉动分量，如式(1)所示.

(1)

气动力的脉动分量又可分为模型相对于静止空气运动产生的空气摩阻力以及模型振动产生的风致作用力，如式(2)所示.

(2)

内置力传感器所测试的动态力也可分为平均分量和脉动分量，如式(3)所示.

(3)

对于竖弯或扭转涡激振动，由达伦贝尔原理以及受力平衡条件，可以得到：

(4)

由式(1)与式(4)可以得到：

(5)

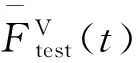
(6)

结合式(2)，式(3)，式(5)及式(6)，得到涡激力具有如下关系：

(7)

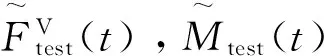
2 风洞试验

2.1 试验模型

某大桥主桥是一座全长1 172 m，主跨700 m的钢-混凝土混合梁双塔斜拉桥，跨径布置为60 m+176 m+700 m+176 m+60 m，主跨及次边跨为闭口流线型钢箱梁，边跨为预应力混凝土箱梁.初步设计方案桥宽B=39.0 m，主梁梁高为H=3.5 m.主梁标准横断面图如图5所示.

图5 某大桥主梁初步设计标准横断面图Fig.5 Preliminary design standard cross-section of a bridge deck

综合考虑风洞试验段尺寸，内置测力传感器的精度和量程以及装置内置框的尺寸，采用1∶30几何缩尺比设计刚体节段模型，试验模型尺寸为1.54 m×1.30 m×0.12 m，安装如图6所示.

图6 弹性悬挂主梁节段模型Fig.6 Aeroelastic section model of the bridge girder

为提高涡激力的测试精度，选择轻质木板构筑模型悬浮段外衣，以保证足够的刚度以及振动发生时尽可能小的惯性力，增大涡激力在总动态力中所占的比重.试验在湖南大学风工程与桥梁工程湖南省重点实验室的HD-2风洞高速试验段中进行，利用模型中内置的轴向拉压力传感器测试弹性悬挂节段模型在气流中发生涡激共振时的动态合力，采用激光位移计与加速度传感器采集了相应的位移响应时程与加速度响应时程曲线，这些力、位移和加速度信号通过一台16通道的DH5920动态信号测试系统同步采集.模型设置端板以保证二元流动，并在试验前对各种传感器之间的相位差进行标定和修正[11-12].

综合考虑该桥桥位地形以及桥位处风参数研究结果，该桥桥位大风时段风攻角在-3.6°～+3.4°之间，其中8级以上强风样本的平均风攻角为-2.3°.可以推断该桥桥位处出现风攻角α>+3°的可能性较小[13]，因此本文仅选择0°，+3°攻角进行了风洞试验.试验采用的相关参数如表1所示.

表1 箱梁节段模型设计参数

2.2 涡激共振响应

通过风洞试验测试得到两种不同风攻角工况节段模型在整个涡振区间的涡振响应分别如图7和图8所示.可见，当来流攻角α=0°时模型有一个明显的竖向涡振区，涡激振动最大振幅出现于折算风速为7.217、实测风速为2.22 m/s处；来流攻角α=+3°时，模型有两个明显的竖向涡振区，涡激振动最大振幅出现于折算风速为11.05、实测风速为3.4 m/s处.下面所有图中的折算风速Vr=V/(fhD).

图7 α=0°竖弯涡振无量纲振幅Fig.7 Dimensionless amplitude curve of vertical VIV displacement atα=0°

这可以解释为来流攻角改变了系统的气动外形，进而改变了涡脱的形态和位置，使得涡振响应发生了变化.事实上，图8中折算风速为11附近可以观测到较小的峰值，有可能是模型发生了竖弯涡激振动.

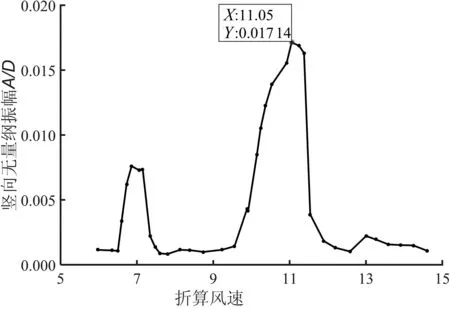
图8 α=+3°竖弯涡振无量纲振幅Fig.8 Dimensionless amplitude curve of vertical VIV displacement atα=+3°

图9和图10分别给出了0°和+3°两组风攻角下，利用激光位移计和加速度传感器直接测试得到的节段模型涡激共振出现最大振幅时对应风速下的位移时程曲线与加速度时程曲线，以及利用位移时程曲线中心差分得到的速度时程曲线.结果表明，α=+3°时模型的最大振幅为2.036 mm，与α=0°时最大振幅为1.579 mm相比有所增大；表明风攻角为+3°时是较不利的.

图10 节段模型实测涡激共振位移、速度、加速度响应时程(α=+3°)Fig.10 Recorded VIV response time history of vertical displacement，velocity and acceleration (α=+3°)

3 涡激力识别与可靠性验证

3.1 涡激力识别

式(2)中的空气摩阻力可以用附加惯性力和附加阻尼力来表示.

(8)

式中：ma为附加质量；ca为考虑了机械阻尼的附加阻尼因数.零风速下，通过强迫振动装置驱动模型做简谐运动并采集模型的位移、加速度时程和动态力时程，由力平衡关系得到如下关系.

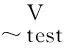
(9)

利用最小二乘法构造误差函数如下：

R(me,ce)=

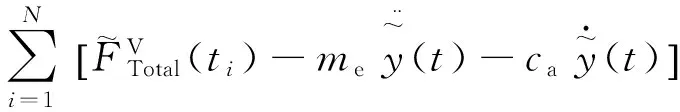
(10)

求解得到ma=1.544 kg/m，ca=3.777 N·s/m2.

图11给出了两组风攻角扁平箱梁发生竖向涡激共振时4个竖向力传感器采集得到的动态合力时程和按照1.2节涡激力识别方法分离得到的涡激力时程曲线.可以看出，α=0°时，动态合力最大最小值分别为5.18 N/m和-5.17 N/m，提取得到的涡激力最大最小值分别为0.55 N/m和-0.30 N/m，涡激力在动态合力中所占比达到5.8%～10.6%；α=+3°时，动态合力最大最小值分别为7.04 N/m和-6.97 N/m，提取得到的涡激力最大最小值分别为0.82 N/m和-0.51 N/m，涡激力所占比达到7.3%～11.6%，与传统的模型两端测力方法相比气动力占比提高，因为传统测力方法包括了整个模型的重量产生的惯性力，此处的三节段测力模型仅包含了轻质外衣部分的惯性力.

(a)α=0°(U=2.22 m/s)

(b)α=+3°(U=3.40 m/s)图11 节段模型竖弯涡振最大时的动态合力和涡激力Fig.11 Vertical total dynamic force and VIF of tested section model at the maximum amplitude of VIV

图12给出了风速为2.22 m/s时模型涡激共振的竖向涡激力时程，可以看出，模型受到的涡激力时程曲线不是标准的简谐波信号.图13为模型在α=0°，风速为2.22 m/s时发生竖弯涡激共振的涡激力进行的频谱分析，可以看出，除主共振频率2.686 Hz外，二阶倍频为主共振频率的5.5%，三阶倍频为9.4%，这解释了涡激力时程信号不是标准正弦信号的原因，倍频成分的出现是因为测试的涡激力中包含有模型位移和速度的相应阶次的非线性自激力项[12].

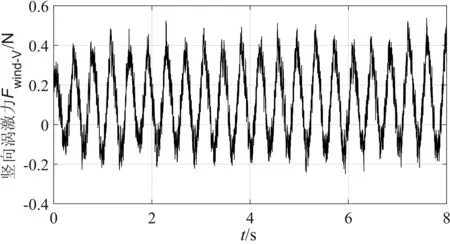
图12 模型涡激共振竖向振幅最大时涡激力时程(α=0°)Fig.12 VIF time history of tested section model at the maximum amplitude of VIV (α=0°)

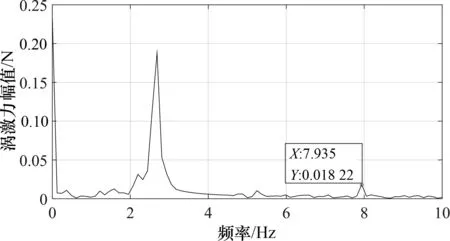
图13 模型涡激共振竖向振幅最大时涡激力幅值谱(α=0°)Fig.13 VIF amplitude spectrum of tested section model at the maximum amplitude of VIV (α=0°)

3.2 涡激力可靠性验证

为检验前述涡激力的测量精度，利用单自由度振子模型来描述自由悬挂试验中的竖向涡激振动过程[11-12，14]，如式(11)所示.

(11)

(12)

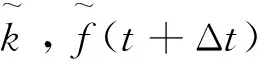
(13)

速度和加速度可以表示为：

(14)

(a)α=0°(U=2.22 m/s)

(b)α=+3°(U=3.40 m/s)图14 数值反算位移与实测位移对比Fig.14 Comparison of calculated displacement and recorded displacement

系数γ，β分别取0.5和0.25.基于该方法所得到的数值反算位移仅由识别得到的涡激力这一唯一变量计算得到，因此反算位移时程与实测位移响应对比可以反映测试结果的准确性.将实测的涡激力时程代入式(12)～式(14)，得到数值反算的位移时程与涡振发生时同步测得的位移时程对比曲线，如图14所示，其中的实测结果进行了低通滤波处理，低通滤波器截止频率为20 Hz.

可以看出，反算位移与实测位移吻合度很好，表明测试的竖向涡激力是准确可靠的.

4 涡激力特性

4.1 频率变化曲线

图15给出了两种风攻角下涡激共振及邻近风速区间采用力信号和位移响应信号分析得到的模型振动频率曲线，矩形框内表示涡振的风速锁定区间.可以看出，力信号与位移信号相比，测试得到的模型主振动频率完全吻合；模型起振前后，模型主振动频率为固有竖弯基频2.563 Hz；锁定区间内主振动频率由2.563 Hz增加到2.686 Hz；消振前后模型主振动频率维持较长风速段不变，最后恢复至结构自振频率2.563 Hz.

(a)α=0°

(b)α=+3°图15 典型涡振区间范围内振动频率随无量纲风速变化曲线Fig.15 Curve of vibration frequency varying with reduced wind velocity for typical VIV range

可见，涡激共振时振动频率增加约4.7%，这体现了涡激共振时由于模型运动产生的气动刚度的影响，这一点根据下文的Scanlan经验非线性模型中与运动位移相关的气动刚度项也可以看出.但是，由于涡激共振的限幅特性，气动刚度项的作用比较小，因此在很多应用和研究中被忽略.

4.2 力与速度相位差及能量转化

模型涡激力与位移响应之间的相位关系可以反映涡激力的做功状态.通过对扁平箱梁节段模型涡激共振发生时的竖弯涡激力与速度响应的互功率谱分析，可以得到二者之间的相位差随折算风速的变化情况.

图16给出了扁平箱梁节段模型在两种风攻角下涡激力与速度时程相位差随无量纲风速变化曲线.可以看出，在涡振锁定区间内，扁平箱梁节段模型竖弯涡激力和速度之间的相位差随折算风速增加而增加，且相位差基本上为[-90°,90°]，表明涡激力在锁定区间内始终在做正功.

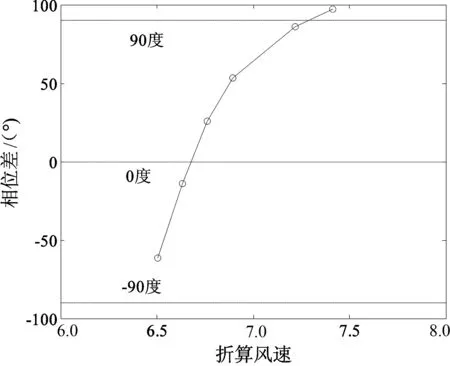
(a)α=0°

(b)α=+3°图16 涡激力与位移时程相位差随无量纲风速变化曲线Fig.16 Curve of phase difference between VIF and displacement varying with reduced wind velocity

图17为该模型竖弯涡激力做功随折算风速的变化曲线.可以看出，在最大涡振振幅对应风速之前，涡激力做功随折算风速增大而增大；当涡振振幅曲线进入下降段，涡激力做功随折算风速增加而减小，最后做功为零.这种特性与涡激振动响应的自激限幅特性是一致的.

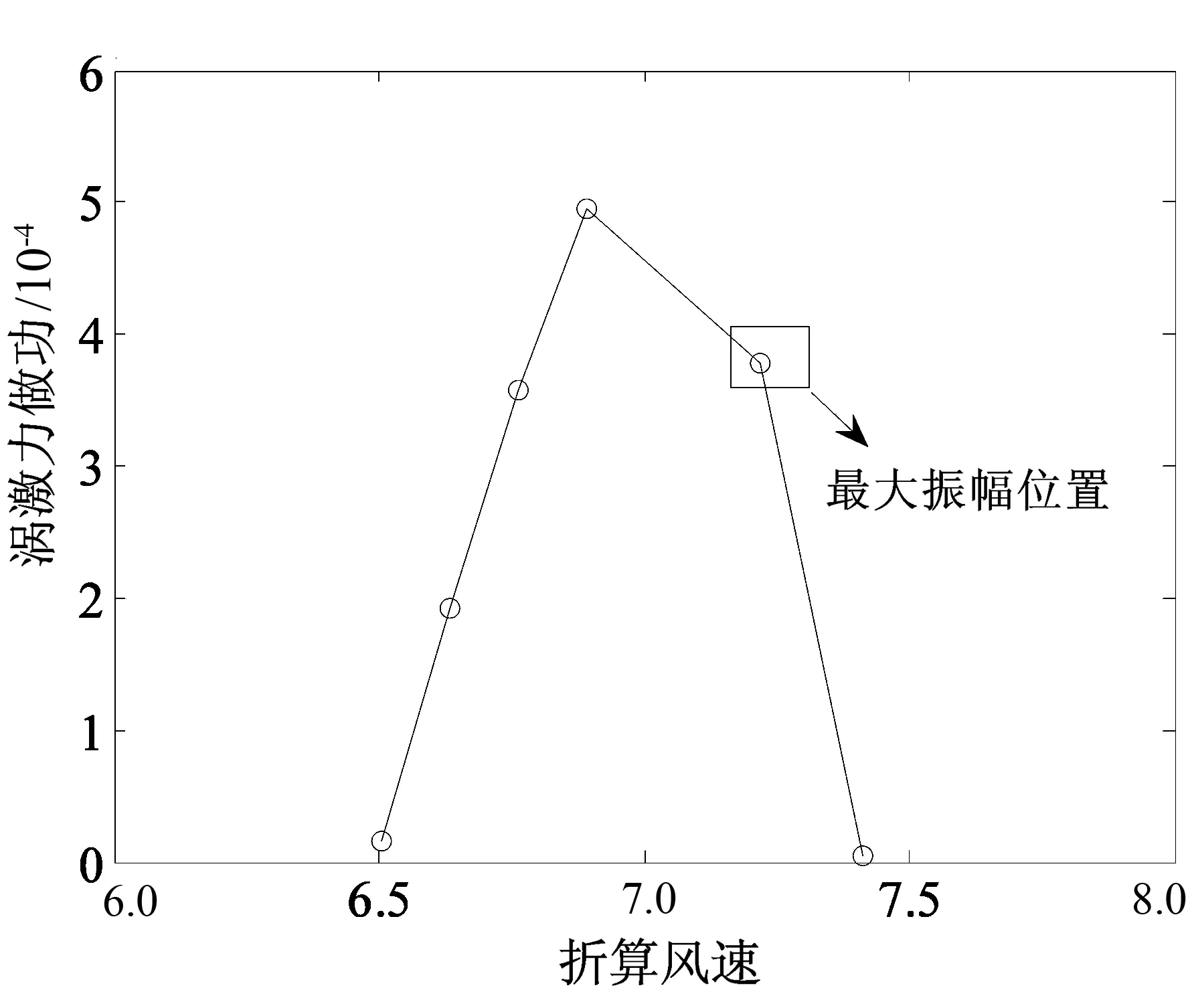
(a)α=0°

(b)α=+3°图17 涡激力做功随无量纲风速变化曲线Fig.17 Curve of the work applied by VIF varying with reduced wind velocity

4.3 Scanlan非线性涡激力参数识别

Scanlan于1986年提出了描述涡激力的经验非线性模型[12-16]，通过引入一个三次的非线性气动自激力项来描述涡激力的非线性性质.

(15)

式中：m为系统质量；ρ为空气密度；U为来流风速；D为模型高度；ω为结构漩涡脱落圆频率；ωn为结构竖弯基频；K为折算频率，K=ωD/U；Y1，Y2，CL及ε均为折算频率K的函数，是待拟合的气动参数.

基于Ehsan和Scanlan提出的位移识别方法[14]，利用衰减到涡振共振发展过程曲线(DTR)识别Scanlan非线性模型参数[17].图18给出了模型在攻角下，来流风速为2.44 m/s时DTR的时程曲线，从而可以得到稳态振动幅值.本文选取s=1 057至s=1 281段时程振动峰值点进行参数识别.

图18 涡激共振时自由振动衰减时程Fig.18 Decaying free vibration time history in VIV range

通过对峰值做对数变换，并作线性拟合得到a=-0.002 448.代入式(17)与式(18)即可得到参数Y1和ε.

(16)

Y1=(2ξK1-a)/mr

(17)

ε=-4a/β2mrY1

(18)

图19给出了扁平箱梁气动参数Y1和ε随涡脱折算频率的变化情况.可以看出，Y1随折算频率先增大后减小，ε随折算频率先减小然后维持稳定，随后继续减小.图20和图21表明，利用Ehsan-Scanlan的位移参数识别方法得到的Scanlan经验非线性模型反算的位移时程与模型实际的位移响应相比，幅值吻合得很好；而基于该方法所得到的竖弯涡激力则与实测涡激力相比差别较为显著，这表明Ehsan-Scanlan的位移参数识别方法无法合理地描述作用于桥梁断面的涡激力.

(a)Y1(K)

(b)ε(K)图19 自由振动法识别的Scanlan经验非线性模型参数随折算频率变化曲线Fig.19 Parameters of Scanlan empirical nonlinear model identified by free vibration method varying with reduced frequency

图20 基于自由振动法识别的Scanlan经验非线性模型参数得到的涡激力与实测涡激力时程对比Fig.20 Comparisons of measured VIF and calculated VIF by Scanlan’s nonlinear model with parameters identified by free vibration method

图21 基于自由振动法识别的Scanlan经验非线性模型参数得到的位移时程对比Fig.21 Comparisons of measured and calculated displacement by Scanlan’s nonlinear model with parameters identified by free vibration method

基于已知涡激力时程，可以采用非线性最小二乘拟合方法对Scanlan经验非线性模型进行涡激力的参数识别.建立误差函数如下：

(19)

式中：FV(t)为t时刻实测涡激力；FVI(t)为拟合涡激力，表示如下：

(20)

通过误差函数R对Y1，ε求偏导数的值等于零可求解得到Scanlan经验非线性涡激力的气动参数，得到ε=-2 934.208，Y1=12.997.由此可以得到拟合涡激力时程曲线如图22所示，与图20相比较可知，该拟合方法得到的涡激力数值与实测数据更接近.

图22 基于实测涡激力最小二乘拟合的Scanlan经验非线性模型参数计算的涡激力与实测值对比Fig.22 Comparisons of recorded and calculated VIF by Scanlan’s nonlinear model with parameters identified by least square fitting method of measured VIF

5 结 论

通过基于三节段测力测振装置的某大桥主梁节段模型涡激振动风洞试验，可以得出如下结论：

1)基于单自由度振子模型，通过模型竖弯涡激力反算得到的模型涡振位移时程与模型涡振发生时同步测试得到的位移时程吻合得很好(见图14)，这表明内置浮框式三节段测力模型装置测试桥梁断面涡激力的精度较高，具备良好的可靠性.

2)测试得到的涡激力频率与位移响应频率在锁定区间内的变化是一致的.涡激力频率随风速增大先稳定为固有竖弯基频，然后在某个风速段略有增大并维持稳定.

3)扁平箱梁节段模型发生竖弯涡激共振时，模型涡激力时程与模型位移响应时程之间的相位差在整个涡振区间内是从0°增加到180°的过程.图16和图17反映扁平箱梁断面的涡激力在整个锁定区间内做正功，且在最大振幅对应风速前，涡激力做功是随折算风速增大而增大的过程，当涡振振幅曲线进入下降段，涡激力做功随折算风速增加而减小，最后做功为零.

4)采用DTR方法识别得到Scanlan经验非线性模型，通过对比发现，拟合得到的涡激力与实测的涡激力时程差别显著，但计算的位移响应与试验响应结果吻合得很好.采用基于实测涡激力时程最小二乘拟合识别并拟合得到的涡激力时程则与实测的涡激力吻合较好.

[1] 张伟，魏志刚，杨詠昕，等. 基于高低雷诺数试验的分离双箱涡振性能对比[J]. 同济大学学报：自然科学版，2008，36(1)：6-11.

ZHANG Wei，WEI Zhigang，YANG Yongxin,etal. Comparison and analysis of vortex induced vibration for twin-box bridge sections based on experiments in different Reynolds numbers[J]. Journal of Tongji University：Natural Science，2008，36(1)：6-11.(In Chinese)

[2] LI H，LAIMA S，ZHANG Q，etal. Field monitoring and validation of vortex-induced vibrations of a long-span suspension bridge[J]. Journal of Wind Engineering and Industrial Aerodynamics，2014，124：54-67.

[3] 张文学，陈伟，李文平. 东京湾大桥风振与控制[J]. 世界桥梁，2005 (4)：60-64.

ZHANG Wenxue,CHEN Wei,LI Wenping.Wind-induced vibration and control of trans Tokyo Bay Crossing Bridge[J]. Journal of Structural Engineering,2005 (4)：60-64.(In Chinese)

[4] 祝志文，夏昌，邓燕华. 钝体矩形断面绕流场机理与主分量分析[J]. 湖南大学学报：自然科学版，2012，39(7)：7-13.

ZHU Zhiwen，XIA Chang，DENG Yanhua. Flow mechanisms around bluff rectangular cylinders and its principle component analysis[J]. Journal of Hunan University：Natural Sciences，2012，39(7)：7-13. (In Chinese)

[5] SARPKAYA T.Fluid forces on oscillating cylinders[J].Journal of Waterway，Port，Coastal and Ocean Division,ASCE,1978,104(3):275-290.

[6] BISHOP R E D，HASSAN A Y. The lift and drag forces on a circular cylinder in a flowing fluid[J].Proceedings of the Royal Society,1964,227(2):51-75.

[7] IWAN W D,BLEVINS R D. A model for vortex-induced oscillation of structures[J]. Jouranal of Applied Mechanics,1974,41(3):581-586.

[8] EHSAN F，SCANLAN R H. Vortex-induced vibrations of flexible bridges[J]. Journal of Engineering Mechanics，1990，116(6)：1392-1411.

[9] SIMIU E,SCANLAN R H.Wind effects on structures:Fundamentals and applications to design[M].3nd ed.New York:John Wiley & Sons,Inc,1996:219-224.

[10] LARSEN A. A generalized model for assessment of vortex-induced vibrations of flexible structures[J]. Journal of Wind Engineering and Industrial Aerodynamics,1995，57(2/3)：281-294.

[11] 陈谨林. 基于浮框式三节段模型的矩形断面涡激力参数识别研究[D].长沙：湖南大学土木工程学院,2014：21-38.

CHEN Jinlin. Research on parameter identification of the vortex induced force based on the floating frame type three segments model with rectangular section[D]. Changsha：College of Civil Engineering，Hunan University，2014:21-38. (In Chinese)

[12] ZHU L D，MENG X L，GUO Z S. Nonlinear mathematical model of vortex-induced vertical force on a flat closed-box bridge deck[J]. Journal of Wind Engineering and Industrial Aerodynamics，2013，122：69-82.

[13] 刘志文，洪涵，梁立农，等. 广东江顺大桥抗风性能试验研究[J]. 湖南大学学报：自然科学版，2015，42(3)：112-119.

LIU Zhiwen，HONG Han，LIANG Linong，etal.Experimental investigation of the wind-resistant performance of Jiangshun Bridge in Guangdong[J]. Journal of Hunan University：Natural Sciences，2015，42(3)：112-119. (In Chinese)

[14] EHSAN F，SCANLAN R H.Vortex-induced vibrations of flexible bridges[J]. Journal of Engineering Mechanics，1990，116(6)：1392-1411.

[15] MARRA A M，MANNINI C，BARTOLI G. Van der Pol-type equation for modeling vortex-induced oscillations of bridge decks[J]. Journal of Wind Engineering and Industrial Aerodynamics，2011，99(6)：776-785.

[16] GUPTA H，SARKAR P P，MEHTA K C. Identification of vortex-induced-response parameters in time domain[J]. Journal of Engineering Mechanics，1996，122(11)：1031-1037.

[17] MARRA A M，MANNINI C，BARTOLI G. Measurements and improved model of vortex-induced vibration for an elongated rectangular cylinder[J].Journal of Wind Engineering and Industrial Aerodynamics，2015，147：358-367.

Study on Characteristics of Vortex-induced Forces on a Bridge DeckBased on a Dynamometric Model with Suspension Frame

NIU Huawei†,WU Runze,CHEN Jinlin,CHEN Zhenqing

(Key Laboratory for Wind and Bridge Engineering of Hunan Province，Hunan University，Changsha 410082，China)

Based on the developed three-segment model with inner dynamometric suspension frame，the vortex-induced vibration (VIV) and the corresponding vortex-induced forces (VIF) of preliminary design deck of a long-span cable-stayed bridge were measured through wind tunnel test with aeroelastic section model. Through the analysis of VIV under 0° and +3° wind attack angle，the dynamometric model was proved to be effective for measuring aerodynamic forces on bridge deck. In addition，the recorded displacements and forces of VIV under different wind attack angles were compared，and the varying curves of VIV frequency，phase difference between force and displacement as well as the work applied by VIF in lock-in range were also discussed. The results show that the dynamometric model can measure the aerodynamic forces simultaneously when the model is vibrated. Furthermore，for the lock-in range，the VIF frequencies were the same as displacement frequencies，and the phase difference between VIF and displacement increased with the wind speed growth，while the work applied by VIF demonstrated the trend of increasing firstly and then decreasing.

bridge;vortex-induced vibration;vortex-induced force (VIF);dynamometric model;three-segment model

U441.3

A

1674-2974(2017)11-0135-10

10.16339/j.cnki.hdxbzkb.2017.11.016

2016-09-14

国家自然科学基金资助项目(51478181, U1534206),National Natural Science Foundation of China(51478181,U1534206)；桥梁结构抗风技术交通行业重点实验室开放课题基金，KLWRTBMC Fund

牛华伟(1978—)，男，河南驻马店人，湖南大学高级工程师，博士

†通讯联系人，E-mail: niuhw@hnu.edu.cn