东北落叶松材单向顺纹受拉损伤模型

谢启芳，张利朋，王龙，钱春宇

(1.西安建筑科技大学 土木工程学院，陕西 西安 710055；2.机械工业勘察设计研究院有限公司，陕西 西安 710043)

东北落叶松材单向顺纹受拉损伤模型

谢启芳1†，张利朋1，王龙1，钱春宇2

(1.西安建筑科技大学 土木工程学院，陕西 西安 710055；2.机械工业勘察设计研究院有限公司，陕西 西安 710043)

从细观层次揭示木材顺纹受拉破坏的损伤演化机制，是建立木材损伤本构模型的基础.在分析木材宏观及细观构造特征的基础上，将木材等效为若干根并联的受拉木纤维，每根顺纹受拉木纤维等效为弹脆性的受拉微弹簧.基于概率思想，假定受拉微弹簧的极限应变Δ为服从某一分布形式fΔ(x)的随机变量，推导了木材顺纹受拉损伤演化方程.在正确设置木材声发射参数即峰值定义时间(PDT)、撞击定义时间(HDT)和撞击闭锁时间(HLT)的基础上，通过木材顺纹受拉试件破坏过程中的声发射试验确定了受拉木纤维极限应变分布函数的参数，进而建立了木材顺纹受拉损伤模型.分析结果表明，声发射累计振铃计数与木材顺纹受拉细观损伤的累积过程是一致的，可用于反映木材顺纹受拉过程中的损伤演化特征.

木材；顺纹受拉；微弹簧；损伤模型；声发射试验

木材作为木结构的物质基础，分析其在荷载作用下的损伤演化规律，对木结构的力学性能及其在使用过程中的安全分析意义重大.

Aicher等[1]通过声发射技术研究了云杉木在横纹受拉状态下的损伤演化特征.孙建平等[2]利用声发射测试和力学试验相结合的方法，研究了东北常见的阔叶材树种山杨木受弯试件在动态荷载下的声发射演化过程，发现声发射撞击数增加快慢可以体现材料在受力条件下的完全弹性、弹性为主和粘性为主的粘弹性共存3种状态.张志研等[3]依据损伤理论和含有裂纹以及缺陷的木材不同阶段的声发射特征，分别建立了受交变荷载和单向荷载情况下以声发射特征参数表示的木材损伤演变模型，表明以声发射特征参量建立的木材损伤演变模型对木材的损伤预测具有提前性和敏感性.陈志勇等[4]在Simo和Ju针对各向同性材料提出的基于总应变的损伤累积理论模型的基础之上，通过引入损伤因子和使用应力逐步退化模型来模拟木材的应变软化.Khennane等[5]基于不可逆热力学和连续介质力学，建立了基于损伤能释放率的木材顺纹受拉本构模型.Lamy等[6]通过双悬臂声发射试验，揭示了声发射信号中含有的能够反映材料裂缝产生和发展的重要信息.

由于损伤理论在木材本构模型研究中的应用较晚，并且多数研究仍是基于唯象学的，已有研究成果并未揭示木材受力过程中的细观损伤机制.近年来，细观建模方法已越来越多地应用到各种材料的研究中，用于反映宏观现象背后的细观损伤机制，李杰等[7]针对混凝土材料，提出了一类细观损伤物理模型，用于解释混凝土在细观层次上的损伤演化特征.本文在已有材料细观损伤研究成果的基础上，通过对木材宏观和细观构造特征的考察，针对木材顺纹方向受拉的宏观脆性损伤破坏模式，建立了细观弹簧束模型,并借此研究了木材顺纹受拉细观损伤的物理机制，最终得到了木材顺纹受拉状态下的损伤模型.

1 木材的构造特征

1.1 木材的宏观构造特征

在宏观尺度上，木材是由早材和晚材构成的年轮状结构，属于典型的各向异性材料，如图1(a)所示.木材的纵向(L方向)是指与木纤维平行的方向，即顺纹方向；切向(T方向)与径向(R方向)是指与木纤维垂直的方向，即横纹方向[8]，如图1(b)所示.

1.2 木材的细观构造特征

在细观尺度上，木材是由六角形管胞组成的多孔材料[9]，如图2(a)所示，其代表性体积元(RVE)[10]如图2(b)所示.

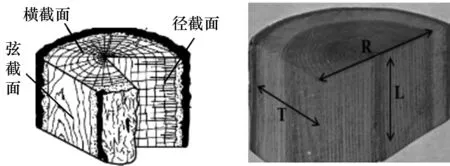
(a)木材宏观构造 (b)木材纹理方向示意图1 木材宏观构造及纹理方向示意图Fig.1 Macroscopic structure of wood

(a)木材多胞状结构 (b)木材的细观RVE图2 木材细观构造Fig.2 Mesoscopic structure of wood

2 损伤变量的定义

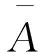
根据平衡条件，有

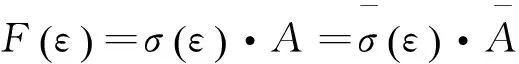
(1)

根据式(1)，有

(2)

将损伤变量定义为：

D(ε)=AD(ε)/A

(3)

可见，式(3)基于缺陷面积定义了损伤变量，简单且物理意义明确，但是由于在材料受力过程中的缺陷面积无法直接通过材性试验测得，并不能完全显化表示木材顺纹受拉过程中损伤演化的具体形式，还需要对损伤演化方程(3)作进一步分析.

3 木材顺纹受拉损伤模型

通过对木材构造特征的考察，将木材的顺纹受拉损伤机制等效为木纤维的脆性断裂，将木材视为由无数根细纤维构成的纤维材料，将其中的每根纤维视作一根细观弹簧，如图3所示.在此基础上可通过图4(c)所示的细观弹簧束模型对木材顺纹受拉试件的有效受拉部分(图4(a))加以反映.图4为木材顺纹受拉模型.

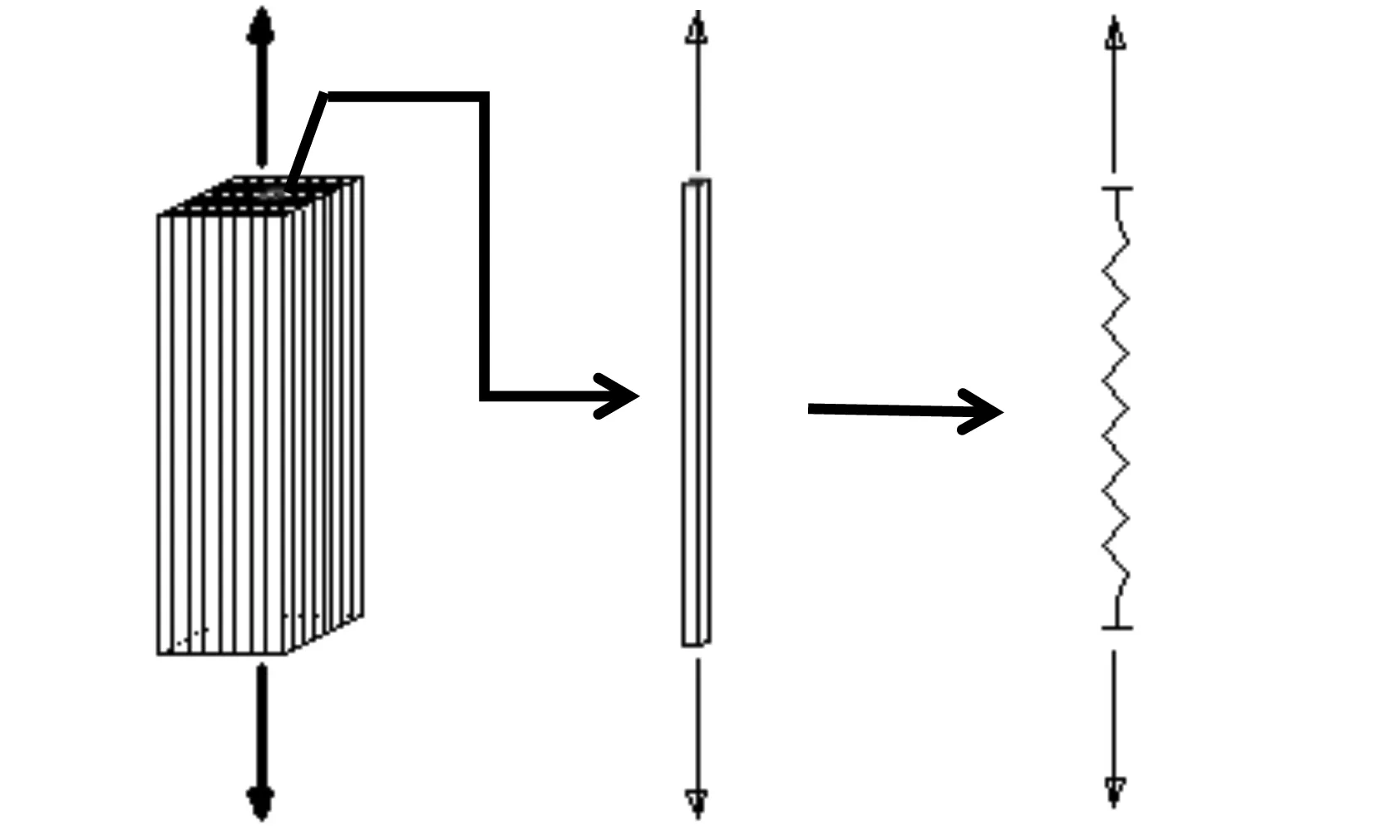
(a)木材 (b)木纤维 (c)木纤维细观弹簧图3 木材的纤维模型Fig.3 The fiber model for wood

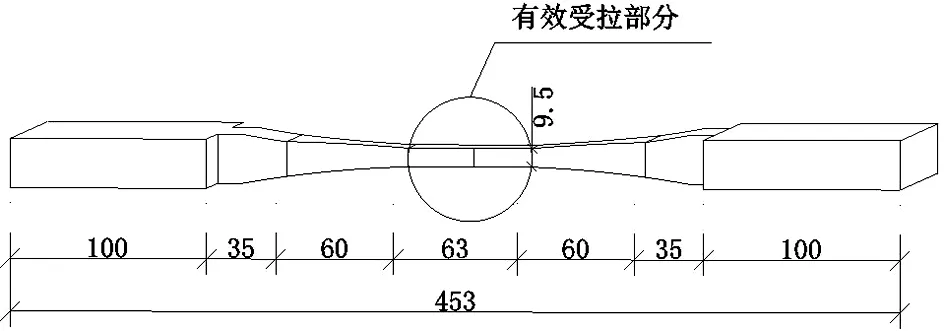
(a)木材顺纹受拉试件

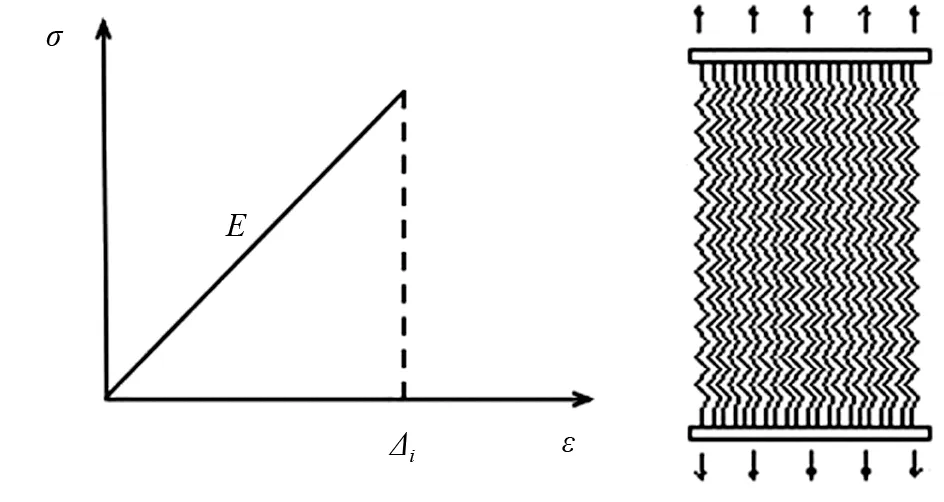
(b)微弹簧本构关系 (c)有效受拉部分弹簧束模型图4 木材顺纹受拉模型Fig.4 Longitudinal tensile model for wood

3.1 木材顺纹受拉细观弹簧束模型的建立

为简便起见，作出以下假定：

1)假定弹簧束模型中的一系列细观弹簧是相互平行且等间距分布的，两端固定于钢板上，且各个弹簧的变形与破坏相互独立.

2)假定微弹簧是理想弹脆性的,且横截面面积与刚度均相同，仅极限拉应变不同.

根据基本假定2)，由于弹簧束模型中所有微弹簧的刚度和面积都是相等的，可用dA表示各微弹簧的截面积；用Δi表示第i个弹簧破坏时的极限拉应变，则其为服从某一分布fΔ(x)的统计变量.

3.2 木材顺纹受拉试件的损伤分析

在木材受载初期的稳定变形阶段，即所有微弹簧均未发生断裂之前，试件中的损伤不发展；随着应变值的增大，试件第1根微弹簧发生断裂后，损伤开始产生累积效应，此后由于微弹簧极限拉应变的随机性导致了微弹簧断裂的随机性，也即产生了损伤的非线性累积效应.

设在弹簧束模型中，微弹簧的数量为Q；第i根微弹簧的拉伸应变为εi；则由于微弹簧的断裂损伤而退出工作的微弹簧的面积AD(ε)为：

(4)

式中：H(ε-Δi)为Heaviside函数，其表达式如式(5)所示.

(5)

特别地，当Q→∞时，弹簧束模型便连续化为木材顺纹受拉试件.将式(4)代入式(3)中，得

(6)

为进一步确定木材顺纹受拉试件的损伤演化规律，需对式(6)进一步分析.

引入中间变量ξ(x)，并令其为Heaviside函数，则其表达式为：

ξ(x)=H(ε-Δi)

(7)

由于微弹簧的极限应变Δi为服从某一分布的随机变量，则知ξ(x)也为随机变量，由Heaviside函数表达式可知，ξ(x)服从(0～1)分布，且其分布规律为：

P[ξ(x)=1]=P[H(ε-Δi)=1]=

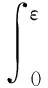
(8)

(9)

由于ξ(x)为随机变量，可知损伤变量D(x)为与ξ(x)具有相同分布的随机变量，与ξ(x)具有相同的均值与方差.其均值为：

(10)

经上述分析可知，式(6)表示的D(ε)为木材顺纹受拉状态下的随机损伤演化方程.

设Dm(ε)为木材顺纹受拉均值演化损伤变量，则其表达式为：

(11)

式(11)代表了木材顺纹受拉损伤均值演化规律，在某种程度上带有确定性损伤的性质，因此，为了加以区分，称D(ε)为随机损伤演化方程，而直接称Dm(ε)为损伤演化方程.

根据以上分析，要确定木材顺纹受拉损伤演化方程，需要知道微弹簧的极限应变分布规律.

4 微弹簧极限应变分布函数形式假定

目前，直接确定微弹簧极限应变分布函数fΔ(x)较为困难，通常做法是首先人为假定其分布形式，然后确定其分布参数值，与试验结果比较验证其有效性.这种方法在钢、混凝土以及岩石等材料的损伤模型研究中已广泛应用[7,10]，在木材损伤研究中虽有应用，但选取的分布函数形式则是直接借鉴其他材料损伤的研究成果[3].

本文根据声发射试验结果，假定木材顺纹受拉细观弹簧束模型中微弹簧的极限应变Δi所服从的分布函数为：

(12)

式中：a，b，c为材料常数，与材料类型有关.

将式(12)代入式(11)中，得到木材顺纹受拉损伤演化方程为：

(13)

由式(13)可知，确定了参数a，b，c的值，就确定了木材顺纹受拉损伤演化规律，声发射试验是目前较为常用的方法.

5 木材顺纹受拉声发射试验

一般来说，声发射(Acoustic Emission,AE)可以定义为材料在形变过程中由于微破裂致使聚集的能量突然释放而产生的一种弹性波.显然，那些微破裂是材料内部损伤的结果.可以肯定，在声发射与材料损伤之间存在着必然联系，换句话说，声发射活动代表着木材微损伤的程度[11-12].

假设在木材顺纹受拉弹簧束模型中：n为微弹簧单元单位面积损伤产生的声发射数；A为无损伤时的截面面积；ND(ε)为应变为ε时的累计声发射振铃数；Ntot为完全损伤时的累积声发射振铃数.那么，损伤面积AD(ε)将产生的声发射数为：

ND(ε)=nAD(ε)

(14)

将式(14)变换形式并结合式(3)对损伤变量的定义，得

AD(ε)/A=ND(ε)/nA

(15)

D(ε)=ND(ε)/nA

(16)

由式(16)可知，应变为ε时的累计声发射振铃数也具有随机性.

两端均值化处理，可得式(17)：

(17)

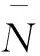
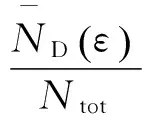
(18)

求式(18)关于应变的导数，有

(19)

由式(18)和式(19)表明：1)声发射与损伤具有一致性，木材顺纹受拉损伤均值演化曲线与声发射累积振铃计数曲线具有相同的变化趋势.2)通过声发射累积振铃计数曲线便可得到弹簧束模型中微弹簧的极限应变分布形式.

5.1 木材顺纹受拉试件

按照ASTMD143-94[13]制作了12个木材顺纹受拉试件，材料选用东北落叶松材.试件加工前，按照《木结构设计手册》[14]的相关规定对试材进行缺陷(腐朽、木节、斜纹、髓心、裂缝及虫蛀等)情况检查后，认定其材质等级为Ⅱa级.

试件的几何特征和尺寸标注如图5所示.

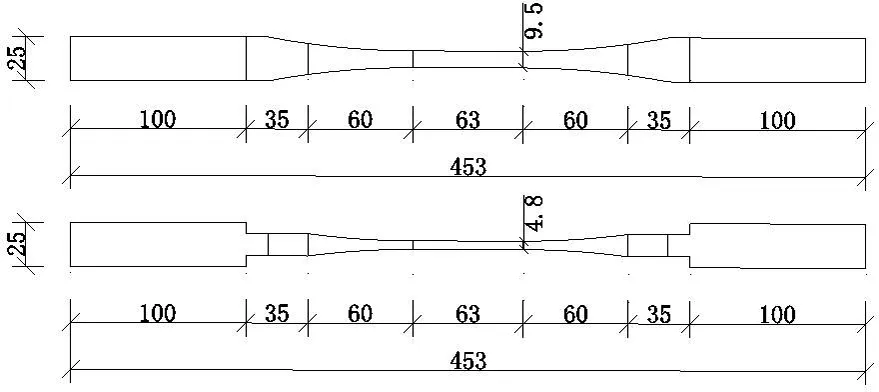
图5 木材顺纹受拉试件(单位：mm)Fig.5 Tensile specimen of wood along the grain (unit: mm)

5.2 声发射试验参数设置

5.2.1 声发射检测门槛值设置

为了获得有效的声发射信号，在加载前必须确定声发射检测门槛值，然后进行消噪处理.通过模拟加载试验[15]，当把参数门限值设置为30 dB时，噪声信号便已经被过滤掉，为提高准确度，试验时将声发射参数门槛值设置为40 dB[16].

5.2.2 声发射时间参数设置

声发射事件参数包括峰值定义时间(PDT)、撞击定义时间(HDT)和撞击闭锁时间(HLT).常用的的声发射参数取值范围参见表1.

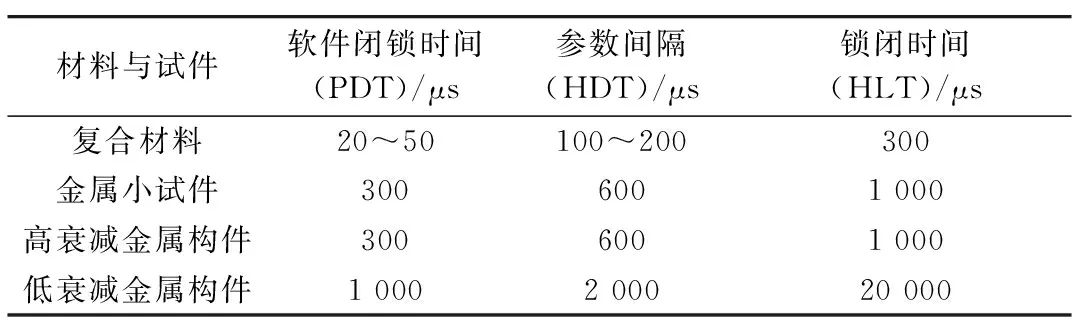
表1 声发射试验时间参数取值范围

由于材性不同，声发射参数值不同.由于木材的离散性较大，在试验前通过断铅试验(每根试件做10次断铅)测得木材的上升时间，得到上升时间为93.11～144.3 μs，取为150 μs.因此，声发射试验时设置的时间参数取值见表2.

表2木材顺纹受拉声发射试验参数设置

Tab.2TheAEparameterssettingofwoodalongthegrainμs

PDTHDTHLT150300450

5.3 试验过程描述

为便于布置传感器，事先将试件固定在试验机上，将传感器涂抹上凡士林后，用胶带固定在试件上，另一端与声发射仪连接好，并检查仪器是否处于正常工作状态，准备工作完毕后等待试验机加载.传感器在试件上的布置见图6.

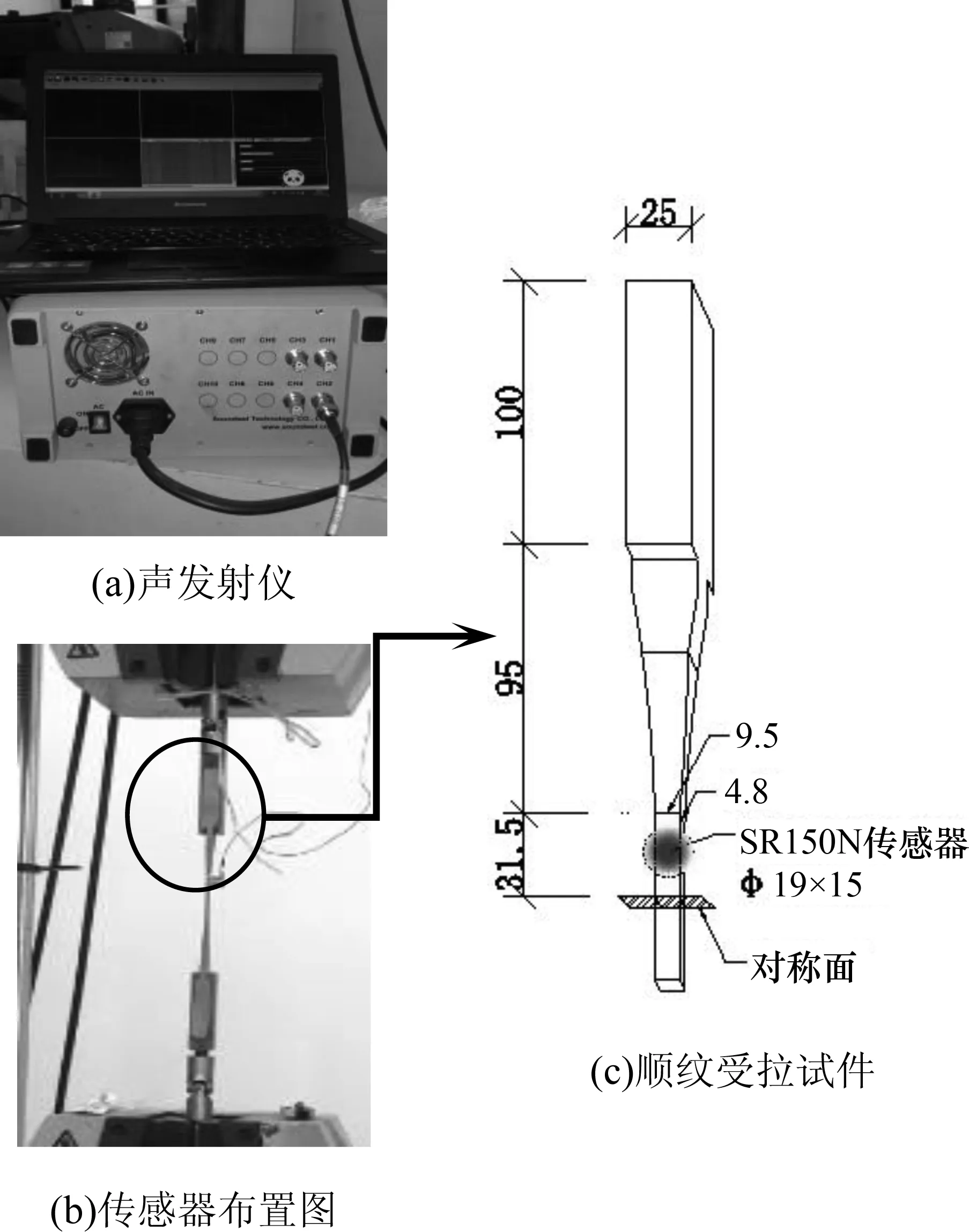
图6 声发射系统及传感器布置图Fig.6 The AE system and arrangement of AE sensor

由于声发射仪与材性试验机分属于2个不同的测试系统，然而测试结果却需要进行应变(时间)统一化处理，即将试验机的时间与声发射仪的时间统一起来，以大大提高了试验结果的真实性.

5.4 木材顺纹受拉声发射特征

木材在受拉过程中的变形和断裂会产生大量声发射信号，这些声发射信号包含的信息可反映木材受拉变形、破坏过程中损伤发展趋势，即木材的声发射信号与其内部损伤存在一定的定量关系[17].

因此，可通过对声发射信号特征参数(声发射能量、振铃、幅度等)的分析，来描述木材的受拉损伤破坏过程.下面以其中一个试件的结果为例加以说明，如图7所示.

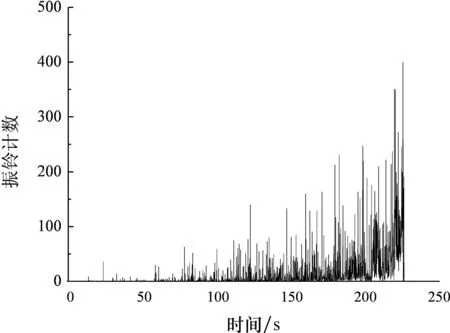
(a)声发射振铃计数

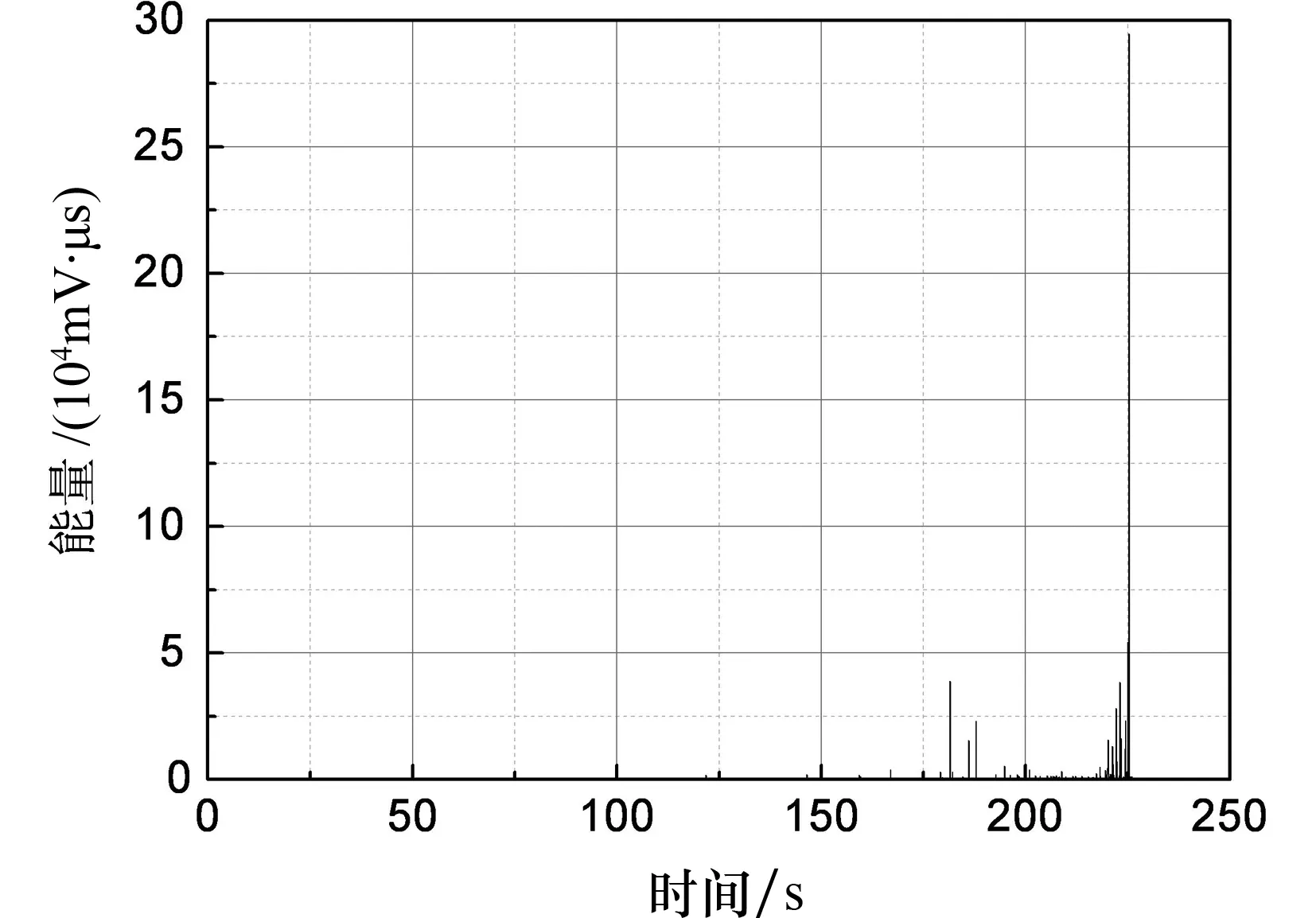
(b)声发射能量计数

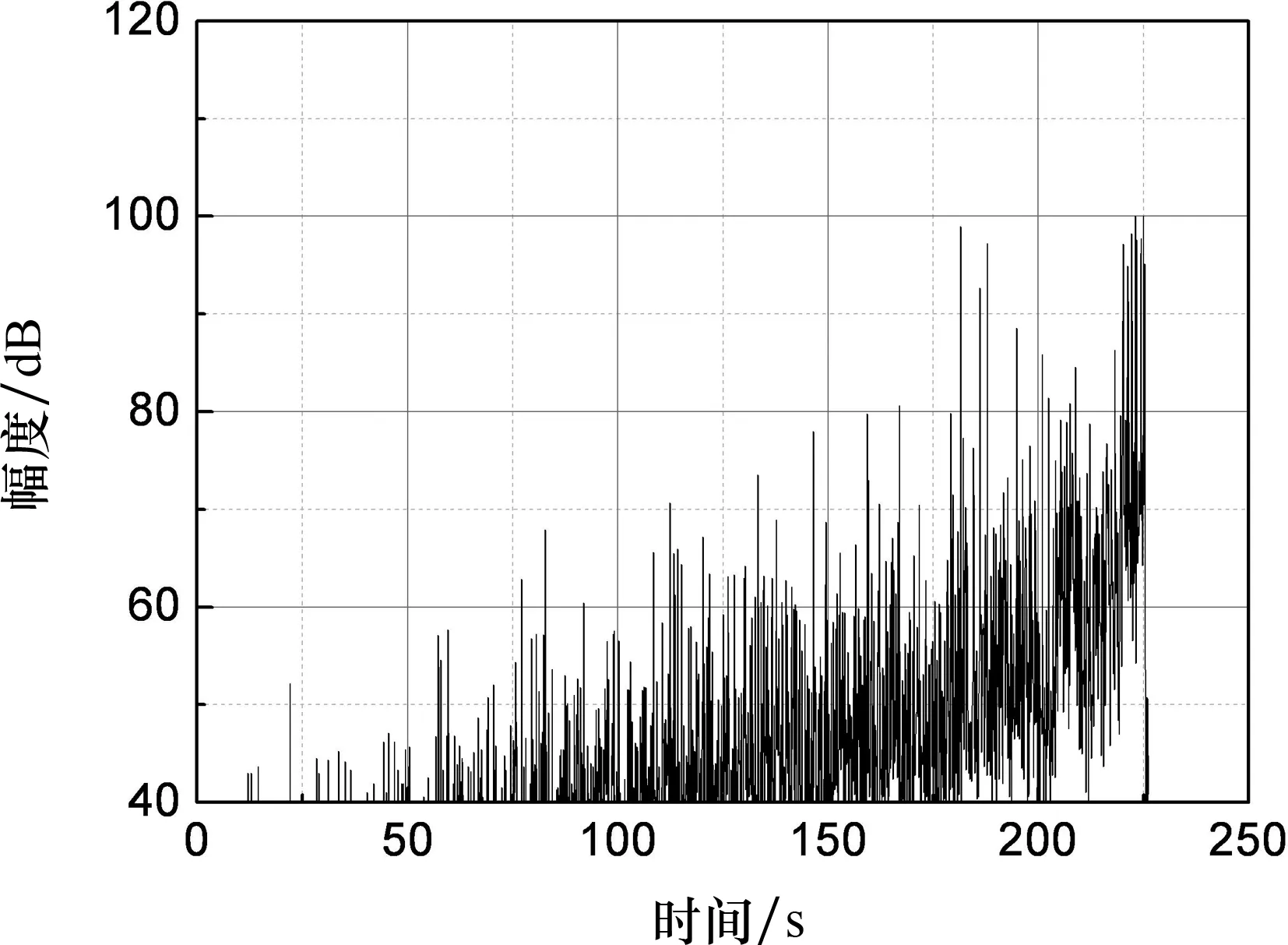
(c)声发射幅度图7 木材顺纹受拉声发射特征参数图Fig.7 The AE characteristic parameter of wood under tensile loading parallel to grain

由图7可见，木材在断裂破坏之前，产生的声发射信号较少，声发射特征不明显；在脆性破坏前的瞬间，产生较高的声发射信号，预示着木材的脆性拉断.

为更加深入分析木材顺纹受拉破坏过程中声发射与荷载之间的密切联系，同时也为进一步说明可以利用木材顺纹受拉声发射信号特征来对木材的损伤加以反映，将应力-应变曲线与累计声发射振铃计数-应变曲线表示在同一图上，如图8所示.由图8可知，木材顺纹受拉表现出弹脆性破坏特征，与图7中呈现的声发射信号特征具有高度一致性，再次说明，通过声发射累计振铃计数这一特征参数可以较好地对木材顺纹受拉破坏过程中的损伤演化规律加以反映.

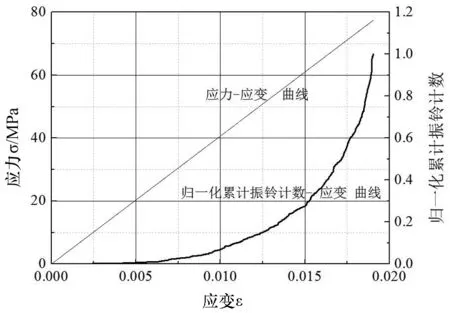
图8 木材顺纹受拉荷载与累计振铃数对应关系Fig.8 The relationship between nominalized AE accumulative events and stress

结合累计声发射计数-应变的特点，将曲线归一化处理后，通过提取出试验结果中极限荷载前段对应的累计声发射计数-应变数据，并利用Gaussian曲线对其进行拟合，如图9所示.可见拟合曲线与试验结果高度符合.

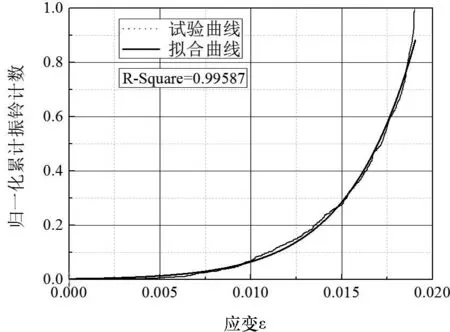
图9 声发射累计振铃计数表示的损伤演化曲线Fig.9 The damage evolution curve using AE accumulative events expression

根据拟合分析，参数a=59 540;b=0.1;c=0.025;相关系数为0.995 87.可见，所采用的分布函数是有效的.

弹簧束模型中微弹簧的极限应变分布规律和损伤演化方程的表达式分别如式(20)和式(21)所示：

(20)

(21)

采用同样的方法，可得到所有试件微弹簧极限应变的分布参数值，如表3所示.

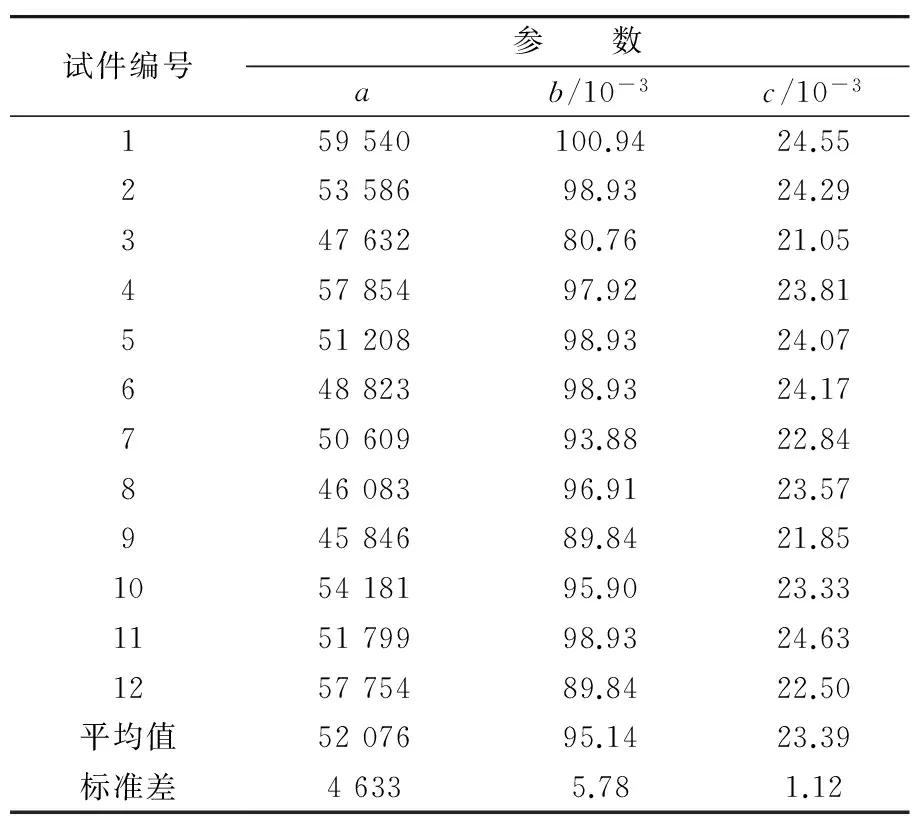
表3 微弹簧极限应变分布参数值

由图8和图9可知，木材顺纹受拉应力-应变曲线呈现出线弹性脆性破坏特征，但是损伤曲线却是非线性的，这需要从不同尺度(破坏的宏观性以及损伤的细观累积性)进行解释.木材顺纹受拉破坏实质上经历了一个从微观到宏观的演化过程，细观损伤从某一局部(初始缺陷处)开始产生并逐渐发展直至试件的宏观破坏.由于试件的尺寸较小，试件在发生脆性断裂之前尚未来得及发生非线性变形，但是脆性断裂的破坏模式却是由微观损伤不断累积所导致的.损伤的非线性也正说明了木材微观极限应变分布的不均性，即表现为损伤的非线性实质上是微纤维断裂的非同时性.

6 结 论

1)通过将木材顺纹受拉力学机制等效为木纤维的脆性断裂以及基于此建立的细观弹簧束模型，建立了木材顺纹受拉损伤模型.

2)通过断铅试验和模拟加载试验得到了木材声发射试验所需相关参数的范围：上升时间为93.11～144.3 μs,PDT为150 μs,HDT为300 μs和HLT为450 μs；声发射门槛值约为40 dB.

3)木材拉伸过程中的声发射累计振铃计数是反映木材损伤的重要特征参数，本文从理论和试验方面都证明了这一点，并指出用其反映木材顺纹受拉损伤演化过程具有较高的可行性，同时也为今后研究木材在其他受力状态下的损伤演化规律提供了一种切实可行的方法.

4)木材顺纹受拉破坏的过程就是木材纤维在受拉荷载作用下不断发生断裂破坏的过程.木材在断裂破坏之前，产生的声发射信号较少，声发射特征不明显；在脆性破坏前的瞬间，产生较高的声发射信号，预示着木材受拉的脆性断裂.用细观弹簧束受拉模型来模拟木材顺纹受拉破坏的物理过程具有十分明确的物理意义.

[1] AICHER S ,HÖFFLIN L,DILLL-LANGER G. Damage evolution and acoustic emission of wood at tension perpendicular to fiber[J]. European Journal of Wood and Wood Products,2001,59(1): 104-116.

[2] 孙建平,王逢瑚,朱晓冬,等. 基于声发射技术的木材损伤过程检测[J]. 福建林学院学报,2006,26(4): 344-348.

SUN Jianping,WANG Fenghu,ZHU Xiaodong,etal. Application of acoustic emission technology to damage process monitoring of wood under the dynamic loads[J]. Journal of Fujian Forestry College,2006,26 (4): 344-348.(In Chinese)

[3] 张志研,赵东. 木材损伤的声发射模式研究[J]. 力学与实践,2009,31(2): 74-77.

ZHANG Zhiyan,ZHAO Dong. Study on the acoustic emission model of wood damage[J]. Mechanics in Engineering,2009,31(2): 74-77.(In Chinese)

[4] 陈志勇,祝恩淳,潘景龙. 复杂应力状态下木材力学性能的数值模拟[J]. 计算力学学报,2011,28(4): 629-634.

CHEN Zhiyong,ZHU Enchun,PAN Jinglong. Numerical simulation of mechanical behavior of wood under complex stress[J]. Chinese Journal of Computational Mechanics,2011,28(4): 629-634.(In Chinese)

[5] KHENNANE A,KHELIFA M,BLERON L,etal.Numerical modeling of ductile damage evolution in tensile and bending tests of timber structures[J]. Mechanics of Materials,2014,68(1): 228-236.

[6] LAMY F,TAKARLI M,AMGELLIER N,etal. Acoustic emission technique for fracture analysis in wood materials[J]. International Journal of Fracture,2015,192(1): 57-70.

[7] 李杰,张其云.混凝土随机损伤本构关系[J]. 同济大学学报,2001,29(10): 1135-1141.

LI Jie,ZHANG Qiyun. Study of stochastic damage constitutive relationship for concrete material[J]. Journal of Tongji University,2001,29(10): 1135-1141.(In Chinese)

[8] OUDJENE M,KHELIFA M.Finite element modelling of woo-den structures at large deformations and brittle failure prediction[J].Materials & Design,2009,30(10):4081-4087.

[9] WITTEL F K,DILL-LANGER G,KRÖPLIN B H.Modeling of damage evolution in soft-wood perpendicular to grain by means of a discrete element approach[J]. Computational Materials Science,2004,32 (3): 594-603.

[10] QING H,MISHNAEVSKY L. A 3D multilevel model of damage and strength of wood: analysis of micro-structure effects[J]. Mechanics of Materials,2011，43(9): 487-495.

[11] 李冬生,欧进萍. 钢绞线拉伸过程中的声发射特征及其损伤演化模型[J]. 公路交通科技,2007,24(9): 57-60.

LI Dongsheng,OU Jinping. Acoustic emission characteristic and damage evolution model of steel strands in tensile test[J]. Journal of Highway and Transporation Researchand Devement,2007,24(9): 57-60.(In Chinese)

[12] 杜伟坊,杜海清. 铝制陶瓷在外应力下裂纹形成及扩展的声发射表征[J],湖南大学学报:自然科学版,1994,21(2): 59-64.

DU Weifang,DU Haiqing. Acoustic emission expression of initiation and growth of crack in alumina ceramic due to thermal stress[J]. Journal of Hunan University:Natural Sciences,1994,21(2): 59-64.(In Chinese)

[13] ASTM D143-94 Standard test methods for small clear specimens of timber[S]. West Conshoho Cken,PA: ASTM International,2007：21-23.

[14] 龙卫国，杨学兵.木结构设计手册 [M].3版.北京:中国建筑工业出版社,2005：26-34.

LONG Weiguo,YANG Xuebing. Wood structure design manual[M].3rd ed. Beijing: China Building Industry Press,2005：26-34.(In Chinese)

[15] 欧阳利军,陆洲导,赵艳林,等.混凝土结构声发射检测参数设置研究[J]. 重庆建筑大学学报,2008,30(5): 37-41.

OUYANG Lijun,LU Zhoudao,ZHAO Yanlin,etal. The setting of acoustic emission detecting parameters in concrete[J]. Journal of Chongqing Jianzhu University,2008,30(5): 37-41.(In Chinese)

[16] 张亚梅，王超，路宜，等.普通混凝土和橡胶混凝土弯曲损伤过程的声发射研究[J]. 湖南大学学报:自然科学版，2010,37(11): 24-30.

ZHANG Yamei,WANG Chao,LU Yi,etal. Investigation of the damage process of ordinary concrete and rubberized concrete under bending load by AE[J]. Journal of Hunan University:Natural Sciences,2010,37(11): 24-30.(In Chinese)

[17] 张明,李仲奎,杨强,等. 准脆性材料声发射的损伤模型及统计分析[J]. 岩石力学与工程学报,2006,25(12): 2493- 2501.

ZHANG Ming ,LI Zhongkui,YANG Qiang,etal. A damage model and statistical analysis of acoustic emission for quasi-brittle materials[J]. Chinese Journal of Rock Mechanics and Engineering,2006,25(12): 2493-2501.(In Chinese)

Damage Evolution Model for Northeast Larch Wood under Parallel-to-grain Tension Load

XIE Qifang1†,ZHANG Lipeng1,WANG Long1,QIAN Chunyu2

(1.School of Civil Engineering,Xi’an University of Architecture & Technology,Xi’an 710055,China;2. China Jikan Research Institute of Engineering Investigations and Design,Co,Ltd,Xi’an 710043,China)

It is very important to explore the damage evolution mechanism of wood under tensile loading at meso-scale，which is the foundation of establishing the damage constitutive model. In this paper，the component characteristics of wood at both macro and meso-scale were analyzed，based on the assumption that wood is equivalent to numerous tension fibers in parallel and every tension wood fiber is equivalent to an elastic brittle tensile micro-spring. The damage evolution equation was derived based on the assumption that the ultimate strains of tensile micro-springs are random variables that obey some form of distribution. Based on the correct setting of acoustic emission parameters PDT，HDT and HLT，the parameters of the ultimate strain distribution function were obtained by tensile acoustic emission tests on Northeast Larch wood specimens along the grain during the failure process. Furthermore，the damage evolution model was established.The analyzing results show a good coherence between the acoustic emission accumulative events and the damage evolution，and the acoustic emission tests are available for the damage assessment during the wood longitudinal tensile process.

wood; parallel-to-grain tension; micro-springs; damage evolution model; acoustic emission test

TU366.2

A

1674-2974(2017)11-0109-08

10.16339/j.cnki.hdxbzkb.2017.11.013

2016-08-22

国家自然科学基金资助项目(51278399)，National Natural Science Foundation of China (51278399)；陕西省自然科学重大基础研究项目(2016ZDJC-23),Shaanxi Province Natural Science Foundation Project (2016ZDJC-23)；国机集团科技发展基金资助项目(13科192号),Science and Technology Development Foundation from China Jikan Research Institute of Engineering Investigations and Design,Co,Ltd(13-192)；西安建筑科技大学创新团体资助计划,Xi'an University of Architecture and Technology Innovation Group Project

谢启芳(1978—)，男，江西赣州人，西安建筑科技大学副教授，博士

†通讯联系人，E-mail: nacy.xie@163.com