欧氏聚类算法支持下的点云数据分割

陈向阳，杨 洋，向云飞

(1. 南通职业大学建筑工程学院，江苏 南通 226007； 2. 上海华测导航技术股份有限公司，上海 201702； 3. 河海大学， 江苏 南京 211100)

欧氏聚类算法支持下的点云数据分割

陈向阳1，杨 洋2，向云飞3

(1. 南通职业大学建筑工程学院，江苏 南通 226007； 2. 上海华测导航技术股份有限公司，上海 201702； 3. 河海大学， 江苏 南京 211100)

欧氏聚类算法是多元统计中的一种重要分类方法，可以将其应用于测绘领域中点云数据的分割。本文首先计算点云数据中两点之间的欧氏距离，将距离小于指定阈值作为分为一类的判定准则；然后迭代计算，直至所有的类间距大于指定阈值，完成欧氏聚类分割。具体步骤为：①利用Octree法建立点云数据拓扑组织结构；②对每个点进行k近邻搜索，计算该点与k个邻近点之间的欧氏距离，最小归为一类；③设置一定的阈值，对步骤②迭代计算，直至所有类与类之间的距离大于指定阈值。试验证明，欧氏聚类算法对不同测量技术手段获取的点云数据均具有适用性，可以成功对点云数据进行分割，分割效果良好。

欧氏聚类;点云数据;分割;算法

聚类分析是依据样品中的个体、对象或主体的特征属性将它们进行分类，使类别之间的个体具有尽可能高的异质性(heterogeneity)，而处于同一类别内的个体则应具有尽可能高的同质性(homogeneity)。图1为聚类分析的示意图[1]。聚类分析的关键是样本之间亲疏关系的判定及分类数的确定，对于变量之间的亲疏关系可通过变量间的相似系数来判定，对于样本数据可以通过样本点间的距离来判定其亲疏相对关系。按照分类的对象可以将聚类分析分为Q型聚类和R型聚类，根据分类的方法又可以将聚类分析分为系统聚类(hierarchical clustering)、快速聚类(K-means clustering)、模糊聚类。聚类分析是一种重要的多元统计分类方法，可应用于许多领域[2]。

图1 聚类分析示意图

点云分割是根据对象的几何、纹理等空间特征对点云数据进行分类划分，使拥有相似特征的点云处于同一划分区内[3]。目前，许多工程应用的前提是对点云数据的有效分割，在激光遥感学科应用领域，要对地物进行识别、重建，首先要对地物进行分类处理[4]。在逆向工程方面，对零件进行探伤、孔洞修复和三维建模，首先要对零件表面扫描分割，然后才能进行基于三维内容的组合利用等[5]。利用欧氏聚类算法，可以成功地将点云数据分割为不同类别的点，同时具有很好的鲁棒性。

1 欧氏聚类分割算法

聚类方法中的每个点都关联一个特征向量，特征向量包含若干个度量值。点云数据的分割是在特征空间中通过聚类的方法进行[6]。聚类分割的原理为：要考察m个数据点，设m个数据点共组成n类，在m维空间数据中定义某种性质的点与点之间的亲疏聚类，然后将具有最小距离的两类合为一类，并迭代计算类之间的距离，直到所有类别之间的距离大于固定阈值，或类的个数小于指定的个数，完成分割[7]。

距离相似性常用于聚类分析，点间距离远近可判断样本相似性度量，也可反映样本所属类型有无差异。距离越近表明相似性越大，属于一个类型。距离指标可按照数据的性质差别来选用，本文采用欧氏距离作为距离指标[8]。假设每个样品由p个变量描述，可看作空间的一个点，则n个样品就是p维空间中的n个点，则第i样品和第j样品的距离记为

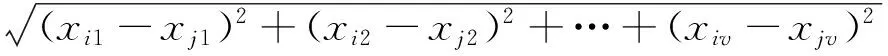
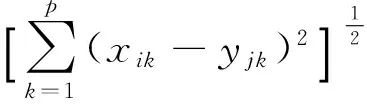
(1)

2 散乱点云索引方式的选择

通过立体摄影测量机、机载LiDAR和三维激光扫描仪等三维测量设备获取点云数据，具有数据量大且分布不均匀的特点。点云数据作为三维领域中重要的数据来源，由海量的离散点构成，呈散乱无序的状态，并不具备传统网格数据的几何拓扑关系[9]。因此，建立离散点之间的拓扑关系是点云数据处理中最为核心的问题，基于此，邻域关系的快速查找才能得以实现。

2.1 Octree和KD-tree

目前，点云空间拓扑关系的建立方式主要有Octree法和KD-tree法。利用Octree法和KD-tree法均可以进行每个激光脚点的k近邻搜索。KD-tree或k维树，是一种带有约束条件的二分查找树，用来组织表示k维空间中的点集合。KD-tree中用指定维度分开每一级别的所有子节点，树的每一级在下一个维度分开，所有维度用完后回到第一个维度。通过判断第一维坐标与根节点的大小来确定点在子树中的左右位置[10]。树的每一级在下一个维度分开，所有维度用完后回到第一个维度。对于点云数据来说，通常只在3个维度中进行处理，建立三维KD-tree，图2为三维KD-tree示意图。

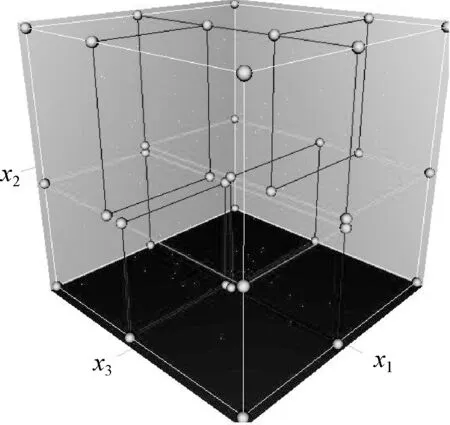
图2 三维KD-tree示意图

Octree结构是对空间实体进行体元剖分，使每个体元具有相同的时空复杂度，对三维空间大小为2n×2n×2n的几何对象再通过循环递归的划分方法进行剖分，从而构成具有根节点的方向图[11]。在Octree中，单个叶节点由相同属性的体元构成；否则要对该体元依次进行递归剖分，直到划分的体元具有相同属性，对于2n×2n×2n大小的空间最多剖分n次，如图3所示。

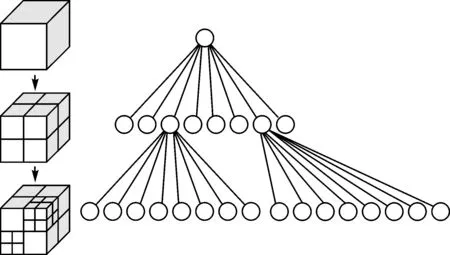
图3 Octree的构建

2.2 两种索引方式搜索性能分析

利用C++语言随机生成样本点分别为100、1000、10 000的点云数据，利用KD-tree法和Octree法分别对样本数据中每个点进行k近邻搜索，并利用C++中计时函数计算程序运行时间。同时，对每个样本数据中每个点的最近点个数(即k的值)，设置为10、25、50，来测试两种方法的搜索性能。表1为测试的结果。

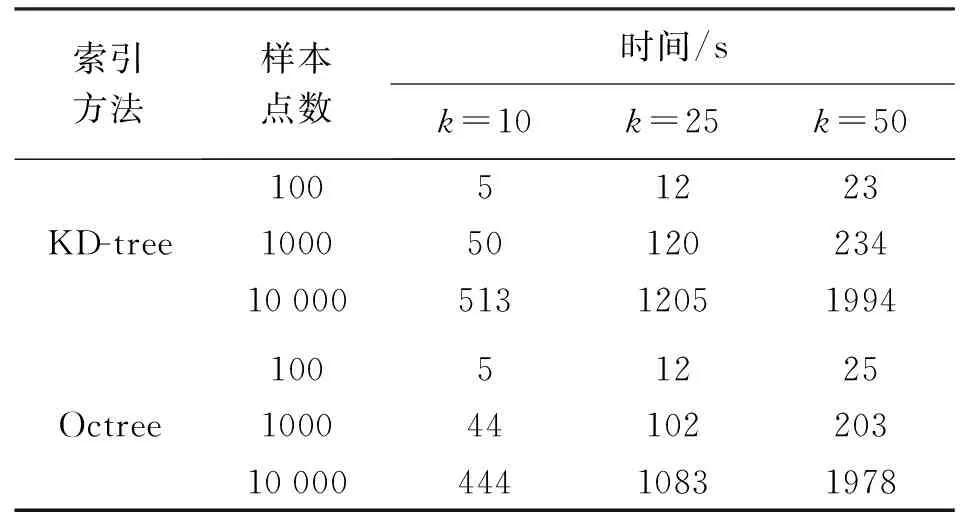
表1 程序运行时间

由表1可知，当样本数据较小时，两种点云索引方式的搜索性能相当。当样本数据量变大时，Octree法相对来说有较高的搜索效率。当数据中搜索的每个点的最近邻点数目(即k的值)变大时，两种索引方式均需要消耗更多的时间，但Octree法表现出更好的搜索性能。机载LiDAR、激光扫描等三维测量设备获取的点云数据，数据量往往很大，有必要寻求一种高效率的点云索引机制[12]。基于以上比较，可以利用Octree法来搜索每个点的最近邻点，进而进行欧氏聚类分割。

3 欧氏聚类分割算法流程

欧氏聚类分割需要将散乱点云模型划分为更小的部分，这样处理的时间就会大大缩短。利用Octree法可以将散乱点云进行三维格网的划分，建立散乱点云之间的拓扑关系。通过建立的八叉树数据结构，可以对每个激光脚点进行邻近点的搜索，计算每个点与邻近点的欧氏距离，将距离最小的归为一类，再在新类之间进行欧氏距离的计算和迭代，直到指定阈值小于任意两类之间的欧氏距离或类的个数小于指定数目，欧氏聚类分割完成[13]。具体算法流程如下：

(1) 对输入的点云数据P建立Octree数据结构。

(2) 建立一个空的聚类集合C和一个队列Q，Q中的每个点都要执行以下操作。

(3) 对于每个点Pi∈P，执行以下步骤：

a. 将Pi点加入当前的队列Q。

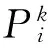
c. 当队列Q中列表中所有点执行以上操作，将Q中的点加入到集合C的列表中，并将Q的列表清空。

(4) 当每个点Pi∈P执行以上操作，且Pi均是集合C中的一部分，算法终止。

4 试验与结果分析

4.1 试验1

4.1.1 试验数据介绍

试验1数据选取利用三维扫描仪对实物扫描获取的点云数据，该数据包含点460 400个，原始数据如图4所示。该数据中包含比较明显的几个类别，分别有平面、圆柱型、条形等，比较适合进行欧氏聚类分割试验。

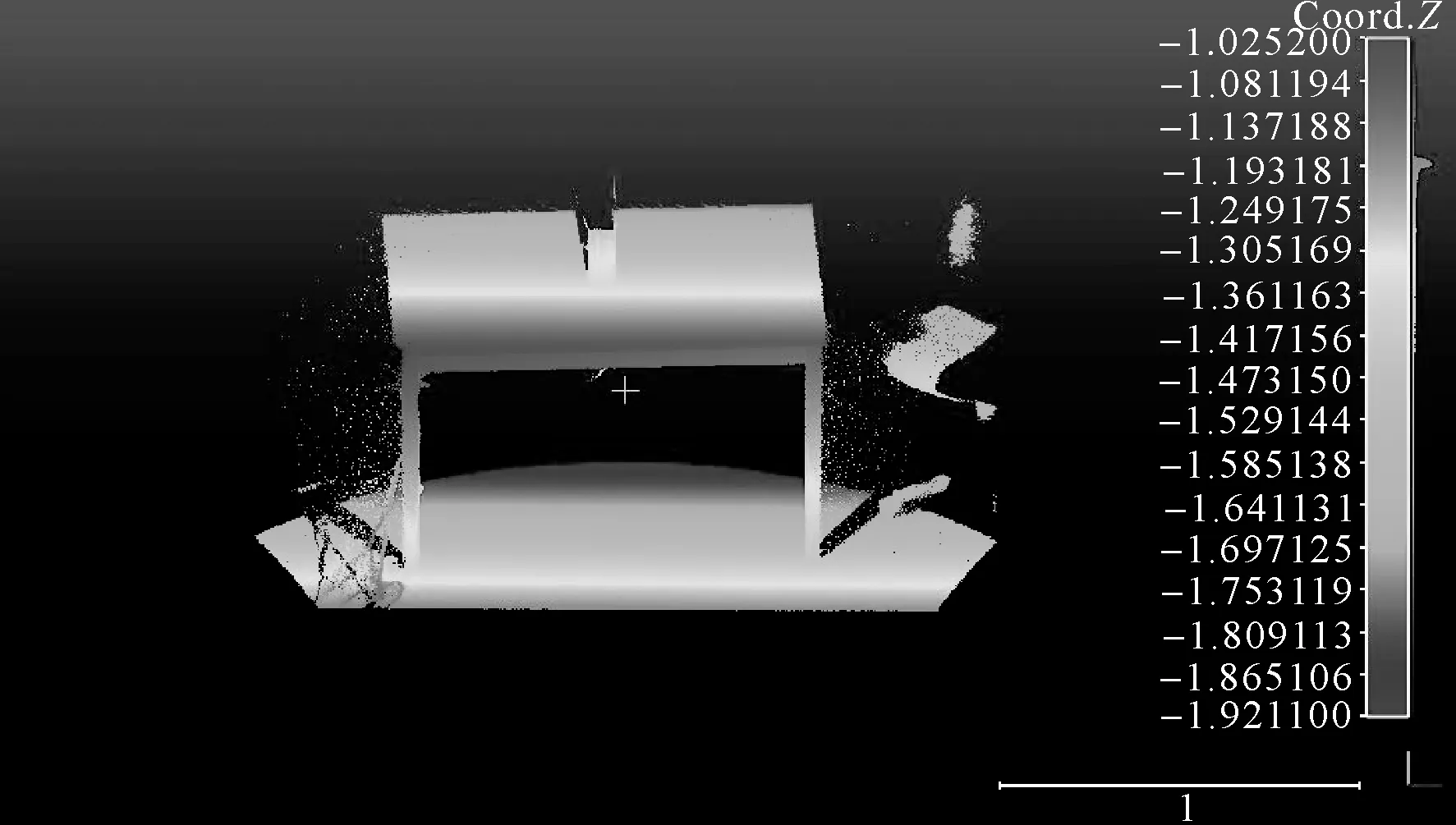
图4 原始点云数据

4.1.2 点云分割试验

通过VoxelGrid滤波器对点云进行下采样。VoxelGrid滤波器通过输入的点云数据创建一个三维体素栅格，然后在每个体素(即三维立方体)内用体素中所有点的重心来近似显示体素内的其他点。利用VoxelGrid滤波器对点云数据进行采样，可保持点云的形状特征不受点数量的减少而改变，大大提高了欧氏聚类的效率。聚类分割的结果如图5、图6所示。

图5 分割出的其他类别

图6 分割出的平面类别

由以上可知，欧氏聚类分割可以成功对三维扫描仪扫描实体的数据进行分割，分割出来的实体具有较相似的类别属性。

4.2 试验2

4.2.1 试验数据介绍

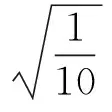
图7 试验区数据

4.2.2 面片提取试验

(1) 对试验数据的点云密度分布进行统计，图8为点云密度分布图。从图8可以看出，深色区域为地面点和近地面点的密度分布，由横轴可知，地面点和近地面点的高程集中在882～894 m之间。

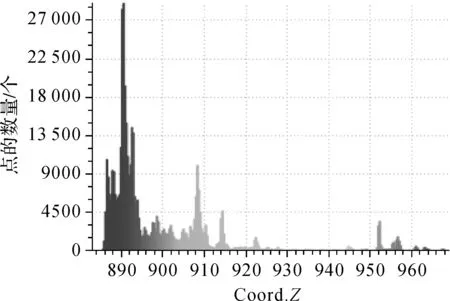
图8 试验区的点云密度分布

利用直通滤波器对试验数据在指定的维度(z轴)上进行滤波，设置滤波的z轴的范围为882～894 m，将在该区间的所有点去除。通过这一操作，对点云数据进行了一个简单的滤波，初步去除了地面点和近地面点，大大减小了面片提取程序的计算工作量。图9为经过直通滤波器进行处理的试验数据，处理后的点云数据去除了大部分的地面点和近地面点，其中包含181 534个点。

图9 简单滤波后的试验区点云数据

(2) 通过VoxelGrid滤波器对点云进行下采样。VoxelGrid滤波器对经过简单过滤后的点云数据创建一个三维体素栅格，由于点云密度为10个/m2，可以设置三维体素体积为0.5 m×0.5 m×0.5 m，在每个体素(即三维立方体)内用体素中所有点的重心来近似显示体素内的其他点。经过VoxelGrid滤波器下采样后,试验区的点云数据中包含134 318个点。图10为下采样前后点云密度分布图，图10(a)为下采样前，图10(b)为下采样后，通过对比前后点云密度分布可以看出，下采样前后保持了点云的形状态特征，只是减小了相应区域的点云密度。

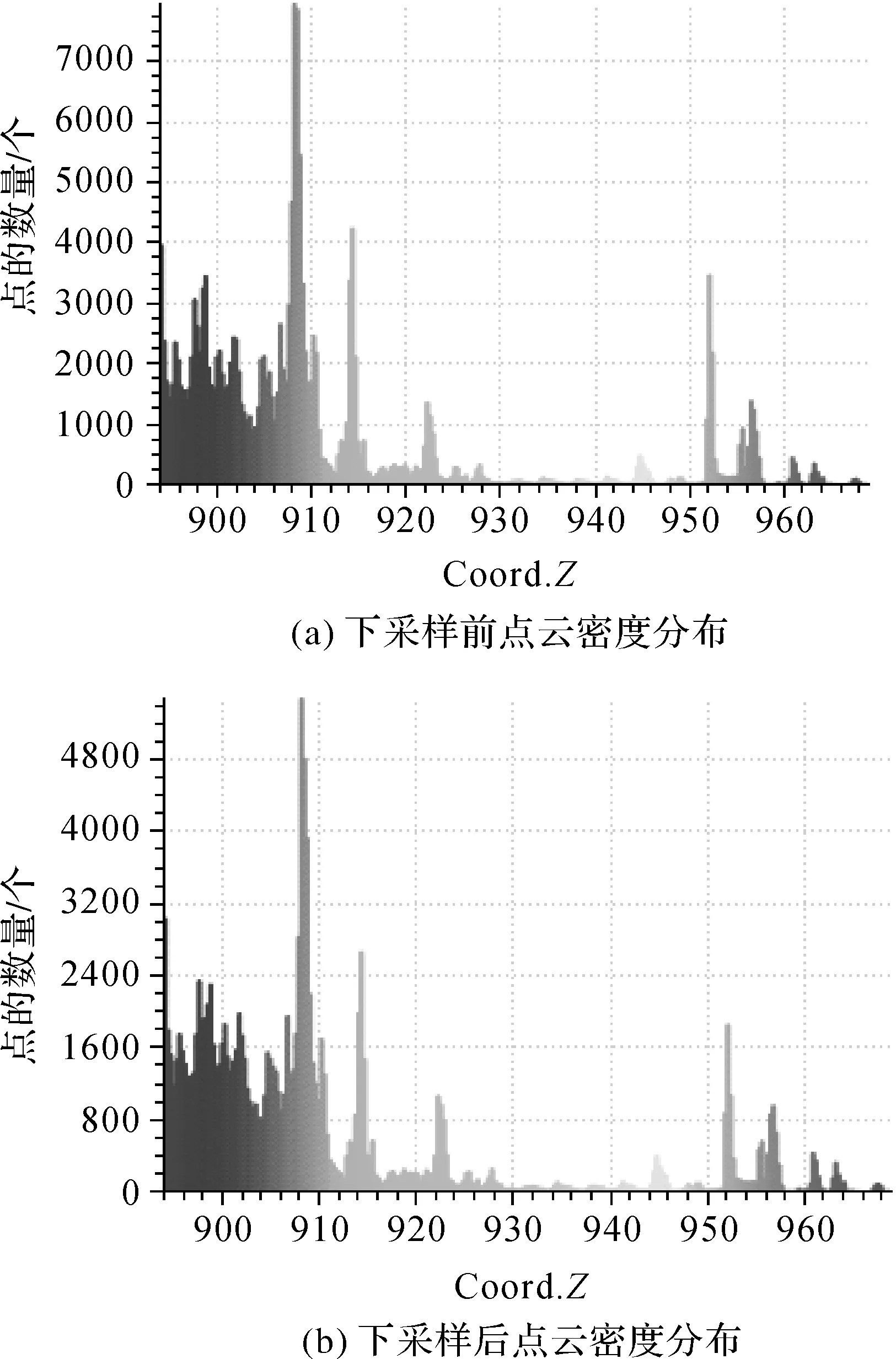
图10 下采样前后点云密度分布

(3) 将检测的平面利用欧氏聚类的方法，设置聚类点之间的容差为0.8 m，每类点最少个数为500个，通过迭代判定，可以将少量、离散的激光脚点去除，从而得到建筑物顶部面片。在CloudCompare中将经过处理的平面模型叠加到一起，得到试验区域所有建筑物顶部面片，图11为对试验区域提取的建筑物顶部面片。

由图11可知，利用欧氏聚类算法可以较成功地提取出试验区域的建筑物顶部面片，提取的建筑物顶部的面片比较完整，去除了一些附属物的激光脚点，用该种方法进行建筑物顶部面片的提取，自动化程度较高。

5 结 语

聚类分析是多元统计中一个重要的分析方法，也是一种分类技术，虽然与多元统计的其他方法相比，还比较粗糙，理论上还不完善，但是应用方面取得了很大的成功，与回归分析、判别分析一起被称为多元统计分析的3大方法。聚类分析可以直接比较各事物之间的性质，将性质相近的归为一类，将性质差别较大的归为不同的类[14]。聚类分析应用非常广泛，经常应用于数学、物理、经济分析等方面。

目前，通过机载LiDAR、激光扫描、立体摄影机等三维测量设备获取的点云数据由大量的离散点组成，点云分割是点云处理的一个重要的方面[15]。通过将聚类分析运用到点云处理，可以很好地进行点云分割。通过对大量离散点建立拓扑组织结构，搜寻每个的k近邻点，计算当前点与邻近点的欧氏距离，将距离最小的归为一类，迭代计算，直到类与类之间的距离大于一定的阈值，完成欧氏聚类分割[16]。通过本文的两个试验证明，无论是机载LiDAR技术获取的大面积的点云数据，还是利用三维激光扫描仪获得的小区域的点云数据，利用聚类分析均能够对点云数据进行有效分割，分割效果良好。

图11 试验区建筑物顶部面片

[1] 龚书林.三维激光点云处理软件的若干关键技术[J]. 测绘通报，2014(6):135-136.

[2] 谭凯，程效军. 激光强度值改正模型与点云分类精度[J]. 同济大学学报(自然科学版),2014,42(1)：131-135.

[3] 李娜，马一薇，杨洋，等. 利用 RANSAC算法对建筑物立面进行点云分割[J]. 测绘科学，2011,36(5)：144-145.

[4] 王书民，李文宁，张爱武. 采用模糊C 均值方法进行激光点云分类[J]. 测绘通报，2016(10):21-24.

[5] 郭波，黄先锋，张帆，等. 顾及空间上下文关系的JointBoost点云分类及特征降维[J]. 测绘学报，2013,42(5)：715-721.

[6] 程晓光，黄先锋，张帆. 机载LiDAR数据的城区树木点提取方法[J]. 测绘科学，2014,39(3):52-56.

[7] 蔡来良,吴侃，张舒. 点云平面拟合在三维激光扫描仪变形监测中的应用[J]. 测绘科学，2010,35(5):231-232.

[8] 姜如波. 基于三维激光扫描技术的建筑物模型重建[J]. 测绘通报，2013(S1)：113-116.

[9] 朱庆伟，马宇佼. 基于三维激光扫描仪的建筑物建模应用研究[J]. 地理与地理信息科学，2014,30(6)：31-35.

[10] 李峰，崔希民，袁德宝，等.机载LiDAR点云城市建筑物面片的提取研究[J]. 大地测量学与地球动力学，2013，33(2)：124-127.

[11] 张玉方，程新文，欧阳平，等.机载LiDAR数据处理及其应用综述[J]. 工程地球物理学报，2008，5(1)：119-124.

[12] MUJA M. Fast Approximate Nearest Neighbors with Automatic Algorithm Configuration[C]∥International Conference on Computer Vision Theory and Applications．Lisbon:VISAPP，2009．

[13] 于海洋，余鹏磊，谢秋平，等.机载LiDAR数据建筑物顶面点云分割方法研究[J]. 测绘通报，2014(6):20-23.

[14] PAULY M，GROSS M，KOBBELT L． Efficient Simpli-fication of Point Sampled Surfaces[C]∥IEEE Visualization． Washington D.C: IEEE Computer Society Press，2002: 163-170．

[15] 罗胜，姜挺,王鑫，等.原始机载LiDAR点云中建筑物激光点的自动提取[J]. 测绘科学技术学报，2013，30(3)：269-273.

[16] 黄先锋，李卉，王潇，等.机载LIDAR数据滤波方法评述[J]. 测绘学报，2009，38(5)：466-469.

MeasurementofPointCloudDataSegmentationBasedonEuclideanClusteringAlgorithm

CHEN Xiangyang1,YANG Yang2,XIANG Yunfei3

(1. Vocational College of Nantong, Nantong 226007, China; 2. Shanghai Huace Navigation Technology Ltd., Shanghai 201702, China; 3. Hohai University, Nanjing 211100, China)

Euclidean clustering algorithm is an important classification method of multivariate statistical analysis. It can be applied to the segmentation of point cloud in survey field. Euclidean clustering algorithm firstly calculates the Euclidean distance between two points. The points’ distance which are less than a specified threshold are divided into a kind. Until all kinds of distance are greater than the specified threshold, it completes Euclidean clustering segmentation. Specific steps are as follows: ① using Octree method set up topology structure of point cloud data; ② for each point conduct K-nearest neighbor search, calculating the Euclidean distance between point and K neighboring points, the minimum is regard as one kind; ③ set a certain threshold, the iterative calculation ② steps until all distances between the classes are greater than the specified threshold. Experiments show that Euclidean clustering algorithm is available to point cloud data obtained from different measuring means. It can successfuly segment point cloud data and the effect is good.

Euclidean clustering;point cloud data;segmentation;algorithm

陈向阳，杨洋，向云飞.欧氏聚类算法支持下的点云数据分割[J].测绘通报，2017(11)：27-31.

10.13474/j.cnki.11-2246.2017.0342.

P23

A

0494-0911(2017)11-0027-05

2017-07-26

国家自然科学基金(41174002)

陈向阳(1975—)，男，硕士，讲师，从事测量工程、卫星定位技术应用研究及数据处理。E-mail:470306595@qq.com