汽车灯具零件控制尺寸公差计算方法研究

2017-12-05李驿林孙艳

汽车与驾驶维修(维修版) 2017年11期

关键词：公差控制点矢量

李驿林、孙艳

（法雷奥照明湖北技术中心有限公司 430056)

汽车灯具零件控制尺寸公差计算方法研究

李驿林、孙艳

（法雷奥照明湖北技术中心有限公司 430056)

快速准确计算车灯零件控制尺寸公差大小，用于控制装配间隙、精密光学件装配精度及结构位置精度。本文基于齐次坐标变化理论，先后阐述了坐标转换原理，建立了数学模型，分别对两类车灯零件进行了讨论。通过坐标旋转、平移等理论计算公式，结合计算机辅助，创建出公差计算工具，解决一般情况的产品控制点公差不易计算、定位优劣无量化等难题。

尺寸公差；定位固定；坐标变换；齐次变换矩阵；罗德里格旋转矩阵

0 引言

近年来车灯造型越来越多，车灯内部件结构复杂，不规则性强。零件间的定位固定受空间约束，易发生首批模具件安装间隙不均、固定不稳定等现象。这样容易造成浪费，并影响开发周期。对此，必须在建模阶段就准确计算公差并分析。

1 理论分析

控制空间中产品6个自由度，需要6个点，即3～2～1原则。它们分别作为正交坐标系中3个方向的定位基准。零件的特征尺寸及公差由这基准得出。车身采用统一的绝对坐标系，但车灯零件间定位并非只按该坐标系设计，往往为空间的一般正交坐标系。在数模上虽然可以方便得到各点的绝对坐标值，但无法方便得到定位坐标系下的值，为计算公差造成困难。因此，需要通过坐标转换来解决该问题。以下公式为点在绝对坐标下的坐标值及矢量方向到任一坐标系的转换公式。

1.1 绝对坐标系中矢量转换为定位坐标系矢量

设Φ为控制点在绝对坐标系下的矢量值为（α β ϒ），第一基准方向在绝对坐标系下矢量为（α1 β1 ϒ1），第二基准方向在绝对坐标系下矢量为（α2 β2 ϒ2），第三基准方向在绝对坐标系下矢量为（α3 β3 ϒ3），则该控制点在定位坐标系下的矢量则为（Φ·A Φ·B Φ·C），即（α·α1+ β·β1+ϒ*ϒ1 α·α2+β·β2+ϒ·ϒ2 α·α3+β·β3+ϒ ·ϒ3）。

2.2 绝对坐标系下点坐标值在定位坐标系下的坐标

设控制点在绝对坐标系下坐标为（x1 y1 z1），定位坐标系坐标原点在绝对坐标系中坐标为（x0 y0 z0）。定位坐标系各坐标轴在绝对坐标系下矢量，第一基准在绝对坐标系下矢量为（α1 β1 ϒ1），第二基准在绝对坐标系下矢量为（α2 β2 ϒ2），第三基准在绝对坐标系下矢量为：（α3 β3 ϒ3）。

则该点在定位坐标系中坐标为：{[（x1-x0）·α1+（y1-y0）)·β1+（z1-z0）·ϒ1] [（x1-x0）·α2+（y1-y0）·β2+（z1-z0）·ϒ2] [（x1-x0）·α3+（y1-y0）·β3+（z1-z0）·ϒ3]}。

1.3 求解定位坐标系原点的绝对坐标系值

(1)求解定位点C投影到直线B上的点坐标

定位点C投影到直线B上的点坐标如下。

x’=mt+xB

y’=nt+yB

z’=pt+zB

其中，m、n、p为直线B矢量方向，xB、yB、zB为直线B上一点（B1或B2），于是得出以下公式。

t=(xC-xB)m+(yC-yB)n+(zC-zB)p

其中，xC、yC、zC为定位基准点C坐标。

(2)求解上式中投影点投影到平面A上的点坐标（即原点坐标）

原点坐标如下。

x=ot’+x’

y=pt’+y’

z=qt’+z’

其中，o、p、q为平面A矢量方向，x’、y’、z’结果见上文，于是得出以下公式。

t’=(xA-x’)o+(yA-y’)p+(zA-z’)q

xA、yA、zA为平面A上一点（A1，A2或A3）。

根据上述公式得出控制点在定位系统中坐标，由公差手册（如NFT-58000等）可得该控制点分别在A、B、C向上公差值。

对于所求矢量方向上公差值可由公式1得出。

如果零件设计的A1、A2、A3正好与方向为A向的平面共面，B1、B2连线矢量方向正好和B向一致，则由上述公式即可求出结果。但常见情况为A1、A2、A3不共面，B1、B2在B向有落差。下面将讨论该一般情形。

2 情形讨论

车灯内部零件较多，有柔性的内、外过度盘等，也有刚性的支架、灯壳等，相应的装配定位设计以及公差控制也有很大不同。现分别讨论这2种情况。

2.1 柔性零件

柔性零件一般为带框或悬臂的过渡盘，容易变形，局部需过约束保证装配质量。可用下列模型来简化并阐述：将可变形产品装到一理想的夹具上，假设6个定位点能一一匹配到夹具对应点。由公式3分别求C到过B1与B2的B向直线上投影，再投影到法向为A并过A1、A2、A3的平面上，共得到6个坐标系统。最后求出控制点在这6个坐标系中，矢量方向上的公差最小值即可。

2.2 刚性零件

刚性零件即车灯产品里的结构件，如灯壳、支架和反光碗等。在做装配设计时不允许过约束，如定位点存在落差，需留定位间隙，该间隙会影响定位精度。在该一般情形中，需考虑定位点之间的相互影响。

模型：刚性体放置于理想夹具上，首先零件上A1’点放置到理论平面A1上，然后依次放置A2’到A2，A’到A3。由于A1’、A2’、A3’在主定位A向上有高度差，导致零件的A1’、A2’和A3’与理论存在偏差，放置后的零件发生歪斜（图1）。接着靠上基准B，同样B1’ B2’在B方向上有落差，这样B1’B2’靠上理论基准B后发生偏转，最后靠上基准C完成定位（图2），所以控制点的位置公差不仅由产品尺寸引起，同时定位造成的偏转也有较大影响[1]。

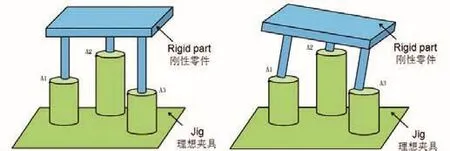
图1 零件发生歪斜

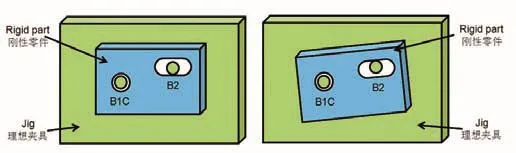
图2 完成定位

(1)第一定位装配计算

第一定位装配计算的目的，是通过一系列旋转保证A1’、A2’、A3’分别落在A1、A2、A3这三个理论平面上。

①首先根据设计图纸定义A向尺寸的主基准，假设为A1’，则A2’、A3’在A方向上的极值可通过公差表（如：NFT-58000等）得到。

②计算在极值状态下的A1’A2’、 A1’A3’和A2’A3’长度尺寸，然后再进行刚性旋转（这些长度尺寸不会改变，可作为约束）。第一次旋转过A1’点并使A2’点落在平面A2上，为了方便计算，虚拟一个辅助本地坐标系，坐标原点为A1’，x轴为A向，y轴为B向，根据右手原则定出Z轴。在这个虚拟坐标系下，A1’坐标为（0 0 0），A2’坐标为（x2 y2 0）；A3’坐标为（x3 y3 z3）。其中，x2和x3分别为A2’和A3’ 与A1’在A向的落差，该落差可求；y2可根据勾股定理求得；y3和z3都根据约束方程组可求。

根据前文提到的坐标转换将A2’和A3’反求到绝对坐标系中，根据矢量行列式公式可求得矢量A1’A2’变换的旋转轴，再根据矢量叉乘定义求得旋转角度值。再由罗德里格旋转公式，可求旋转矩阵matrix a。

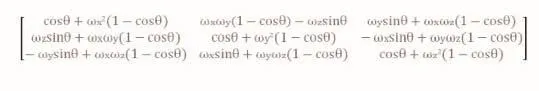
③第二次旋转，用上文中旋转后的A1’A2’作为旋转轴，将经过一次旋转后的A3’点转到理论平面A3上。同理可求旋转矩阵matrix b。

(2)第二及第三定位装配计算

目的是通过一系列的平移和旋转将B1’、B2’分别靠到法线方向为B，并过B1、B2的平面上；将C’靠到法线方向为C，并过C点的平面上。

①将经过第一定位装配变化后的B1’运用平移矩阵matrix c移到理论平面B1上。

Δx、Δy、Δy为经过第一定位装配变化后的B1到平面B1的距离，在绝对坐标系下的分量值。

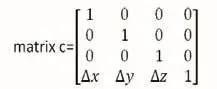
②为方便计算再虚拟一个求解坐标系，其中x轴为平面A法线，y轴为平面B法线，z轴为平面C法线。现将三维坐标系沿x轴压缩为二维坐标系，则B1B2矢量为（矢量B1B2到z的投影矢量B1B2到y的投影）。经过一系列变换后的B1’ B2’矢量为（矢量B1’B2’到z的投影矢量B1’B2’到y的投影）。旋转轴为x轴（即方向A），可求得旋转角，进而求得旋转矩阵matrix d。

③经过上述所有变化后的C’可运用平移矩阵matrix e移到理论平面C上，则零件已在理想夹具上放置完毕。

(3)考虑B1’与B2’点之间的偏差

由于B1’和B2’在定位方向B上存在落差，则B1’,B2’靠上理论平面B1,B2 上时，同样发生偏转。

①设以B1’作为主定位，由公差表可以求出B2’的极限位置。

②第二步中在A平面上投影矢量B1’B2’已得。再求出考虑偏差后的矢量B1’B2’(可根据购股公式求出)。旋转轴为A 向，根据向量点乘定义可以求出前后的旋转角，进而求出旋转矩阵matrix f。将经过一系列变化的c’点通过平移矩阵matrix g移到平面C上。

(4)求出变换矩阵

matrix[transfer]=matrix a·matrix b·matrix c·matrix d·matrix

e·matrix f·matrix g。

对于所有控制点偏转后的坐标都可通过以下公式求得。

coordinator[after]=coordinator[before]·matrix[transfer]

再根据向量点乘定义，可以求出控制点在定义矢量方向上的偏差值tol[rotate]。对于控制点矢量方向上的公差，可分解为定位点偏差引起的旋转影响加上自身零件尺寸影响两部分。即可用以下公式表示。

tol[control]=tol[rotate]+tol[dimension]