归类剖析不等式中的思维误区

2017-12-04河南省淮阳县第一高级中学王梓霖

中学生数理化(高中版.高考数学) 2017年10期

关键词：剖析分母实数

■河南省淮阳县第一高级中学王梓霖

本文对不等式中同学们容易出现的思维误区进行了剖析,希望对同学们的学习和复习有所帮助。

思维误区1——分式不等式求解去分母时不考虑分母的正负

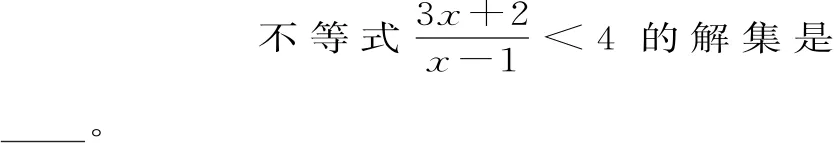
错解:两边同乘以x-1得3x+2＜4(x-1),解得x＞6,所以不等式的解集为(6,+∞)。

剖析:错解中认为x-1＞0,漏掉x-1＜0,从而出现漏解,由原不等式移项得(x-1)＜0,解得x＜1或x＞6。故原不等式的解集是(-∞,1)∪(6,+∞)。

注意点:解分式不等式时,若要去分母需依据“不等式两边同乘正数不改变方向,同乘负数改变方向”对分母大于0和小于0分类求解,每种分类下求交集,最后写出并集。

思维误区2——解含参数的不等式时忽略对最高项系数为零的讨论

如果kx2+2kx-(k+2)＜0恒成立,则实数k的取值范围是____。

A.-1≤k≤0 B.-1≤k＜0

C.-1＜k≤0 D.-1＜k＜0

剖析:将kx2+2kx-(k+2)＜0认定是一元二次不等式,忽略了k=0的情况。

当k=0时,原不等式等价于-2＜0,显然恒成立,所以k=0符合题意。

综上,-1＜k≤0,故选C。

注意点:一元二次不等式恒成立问题常需借助图形进行“双看”:一看开口方向,即看二次项的系数是大于0还是小于0;二看图像与x轴交点情况,即考虑判别式的符号。对于二次项系数为参数的不等式有可能为非一元二次不等式,要对参数讨论。

强化训练2:若不等式mx2+2mx-4＜2x2+4x对任意实数x均成立,则实数m的取值范围是____。

正解:原不等式mx2+2mx-4＜2x2+4x合并同类项得m-2( )x2+2m-2( )x-4＜0,当m=2时,不等式成立。当m≠2时,x∈ -2,2( )。综上,x∈(-2,2]。

思维误区3——线性规划的逆向思维中缺少“运动变化的观念”

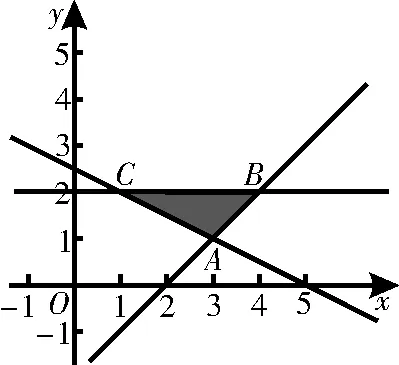
图1

剖析:已知不等式组表示的平面区域为图1中的△ABC及其内部,三个顶点坐标分别为A(3,1),B(4,2),C(1,2)。将目标函数变形得y=-kx+z,当z最小时,直线的纵截距最小。结合动直线y=-kx+z绕定点A的“旋转分析”易经过点(3,1)时纵截距最小。故所求实数k

注意点:已知目标函数在某点处取得最值,可以将目标函数化为标准的斜截式,依据倾斜角和斜率的意义,绕该点灵活 “旋转分析”,准确分析动直线,进而求得斜率的取值范围。

A.[-1,2] B.[-2,1]

C.[-3,-2] D.[-3,1]

正解:作出约束条件表示的可行域,如图2所示的△ABC内部(含边界),其中A(1,1),

已知y=-ax+z的最大值为2a+4,最小值为a+1,说明z在点C处取得最大值,在点A处取得最小值,则有kBC≤

图2

2,所以-1≤-a≤2,即-2≤a≤1,故选B。

思维误区4——线性规划应用中忽略目标函数的几何意义

A.-1 B.0 C.1 D.2

错解:选B。

剖析:误认为最优解在可行域边界顶点处取得,将顶点O,A,B的坐标直接代入比较后得最小值0,没有理解目标函数x2+4x+y2-2y的几何意义。

由x2+4x+y2-2y得x2+4x+4+5,表示如图3所示的区域上任意一点Nx,y( )到定点M-2,1( )的距离d的平方与5之差。

图3

当距离d的最小值为2时,x2+4x+y2-2y取最小值22-5=-1,此时点N的坐标为0,1( )。故选A。

注意点:线性规划中常见的目标函数有:(1)截距型:形如z=ax+by,转化为直线的斜截式,通过“平行移动法”求直线的截距的最值,间接求出a的最值;(2)距离型:形如z=(x-a)2+(y-b)2,可看成可行域内的点P(x ,y)与定点Q(a ,b)连线的距离的平方求解;(3)斜率型:形如z=,可看成可行域内的点P(x ,y)与定点Q(a ,b)连线的斜率求解。