基于共振声学放大原理的涡激振动自发电装置设计与试验

文 晟 李晟华 张建桃 兰玉彬 张海艳 邢 航

(1.华南农业大学工程基础教学与训练中心， 广州 510642； 2.国家精准农业航空施药技术国际联合研究中心， 广州 510642；3.华南农业大学工程学院， 广州 510642； 4.华南农业大学数学与信息学院， 广州 510642)

基于共振声学放大原理的涡激振动自发电装置设计与试验

文 晟1,2李晟华2,3张建桃2,4兰玉彬2,3张海艳2,3邢 航2,3

(1.华南农业大学工程基础教学与训练中心， 广州 510642； 2.国家精准农业航空施药技术国际联合研究中心， 广州 510642；3.华南农业大学工程学院， 广州 510642； 4.华南农业大学数学与信息学院， 广州 510642)

为实现从自然环境中自动获取清洁能源，并给无线传感器和通讯模块供电，基于涡激振动及共振声学放大原理，设计了一种压电自发电装置。首先对位于该自发电装置内的压电悬臂梁复合结构进行力学分析；其次基于计算流体力学数值方法，对绕流圆柱后附加不同板长条件下的流场动力学特性进行分析，以明确悬臂梁长度对脱涡频率和升力、阻力系数的影响规律。利用有限元软件ANSYS对压电悬臂梁复合结构的横向往复振动进行数值模拟，确定了复合结构的横向振动频率随板长L的变化规律。最后对位于该装置两侧的亥姆霍兹共振器的结构尺寸进行优化设计，以使流场的脱涡频率、压电悬臂梁复合结构的一阶横向振动频率和共振器的谐振频率达到一致，从而使压电发电装置产生共振并输出最大的电能。试验结果表明，涡激振动自发电装置在5 m/s的风速下可产生两相峰峰值为6.0 V的开路电压，且上述3个频率达到一致。4～6.25 m/s为该自发电装置的自锁风速区间，在此风速范围内，自发电装置均能产生较大的电压。

涡激振动； 流场分析； 压电发电； 共振； 声学放大

引言

集物联网技术、传感器技术、自动控制技术和通讯技术为一体的农情信息采集系统，可实时采集农田土壤水分肥料信息、农作物生长信息和病虫害杂草信息，是现阶段的研究热点之一[1-2]。传统的化学电池常被用来为数量众多的农情信息采集传感器提供能源[3]，但化学电池的容量有限，能量密度低，使用时间短，且废弃的电池会破坏水体和土壤[4]，因此如何为这些传感器提供持续清洁能量源的研究越来越受到重视[5]。随着微机电系统技术及集成电路的迅速发展，传感器节点能耗进一步减低，这使得直接从自然环境中获取能量并为传感器供能成为可能[6]。风能作为一种清洁能源广泛存在于自然界中，传统的涡轮风力发电机组由于体积较大、造价较高且需定期维护，对于数量众多的传感器网络节点不是理想的能量源[7]。具有压电效应的压电材料能在外力作用下直接产生电荷，易于整合到系统且无电磁干扰，更适合为无线传感器及通讯模块提供电能[8]。

针对目前压电风力发电产生的电压较低、风能利用率不高等问题[9]，本文基于涡激振动及共振声学放大原理，设计一种压电自发电装置。其利用涡激振动原理使位于该自发电装置内的压电悬臂梁复合结构产生横向振动并输出电能，同时将位于该发电装置两侧的亥姆霍兹共振器(Helmholtz resonator)作为风能放大装置。利用流场数值分析和参数优化设计，使脱涡频率、压电悬臂梁复合结构的振动频率和共振器的谐振频率保持一致，且声场放大比率达到最大，最终使该装置产生共振并输出最大的电能。此外，对该发电装置进行流场分析和发电试验，得到外界风速对其自发电能力和振动特性的影响规律，为该装置的工程化应用打下基础。

1 涡激振动自发电装置结构与工作原理

设计的涡激振动自发电装置如图1所示，由腔体、绕流圆柱、压电悬臂梁复合结构、基座、亥姆霍兹共振器、支架、导线、整流电路和蓄电池等部件组成。其中，中空腔体的两侧对称布置了2个结构相同的亥姆霍兹共振器。压电悬臂梁复合结构包括一块柔性金属基板和2片附于该基板两侧的柔性压电材料，其一端固定于腔体内部的基座，另一端与绕流圆柱配合。

图1 自发电装置结构示意图Fig.1 Schematic diagram of self-generating device1.腔体 2.绕流圆柱 3.压电悬臂梁复合结构 4.基座 5.亥姆霍兹共振器 6.支架 7.导线 8.整流电路 9.蓄电池

当外部气流从腔体前端流入，并经过绕流圆柱时，在满足一定的条件下(雷诺数Re大于150)，气流的边界层在绕流圆柱表面摩擦阻力和压差阻力的共同作用下发生分离，并形成特定频率的交替涡旋，即卡门涡街[10]。同时，涡旋脱落的反作用力又使得绕流圆柱和压电悬臂梁复合结构产生周期性的横向振动，带动柔性压电材料分别产生拉、压应力，从而利用压电效应产生电能。

亥姆霍兹共振器是一种声波加强设备，当卡门涡街的气流扰动波进入共振器时，共振器的剪切层对其进行放大，形成涡环结构并在上游剪切层诱发新的扰动。当这两种扰动匹配时，共振器不断受到周期性激励产生流体自激振荡，并在其出口处形成自激振荡脉冲射流[11]；射流冲击绕流圆柱，进而加大压电悬臂梁复合结构的横向振动幅度。

当卡门涡街的脱涡频率、压电悬臂梁复合结构的横向振动频率以及亥姆霍兹共振器的共振频率一致时，悬臂梁复合结构将达到共振状态，此时其横向振动幅度达到最大，从而使柔性压电体输出最大的电能。电能经整流电路整流后至蓄电池中储存起来。自发电装置的3种工作状态如图2所示。

图2 自发电装置的3种工作状态Fig.2 Three operating states of self-generating device

2 控制方程

2.1 圆柱绕流

研究表明[12]，流体经过圆柱后的尾流形态与雷诺数Re直接有关：当Re较小时，流体流经圆柱时无分离流动；当Re大于5时，流体在圆柱体尾部形成一对对称的滞留涡(图3a)；随着Re的增大，尾迹开始失稳并出现周期性的振荡，滞留涡则交替脱落而演化成稳定的层流涡街，当Re处于3102～3105亚临界区范围内，尾迹已经完全变成湍流涡街(图3b)；当Re处于3105～3.5106临界区内，圆柱的边界层受到湍流涡街尾迹的影响从层流分离转变成湍流分离(图3c)。其中，雷诺数Re表达式为[13]

(1)

式中ρ——流体密度，kg/m3

v——流场特征速度，一般取入口处的平均流速，m/s

D——绕流圆柱直径，m

μ——流体动力粘度，Pa·s

图3 圆柱绕流随Re变化的等值线涡量图Fig.3 Equivalence vorticity graphs of flow around a circular cylinder with Re

当流体经过单圆柱后形成卡门涡街时，在有限流道内涡旋的脱落频率f为[14]

(2)

其中

(3)

式中St——斯特劳哈尔数，表示流体动能与系统固有能的相对关系

ε——圆柱两侧弓形面积与进气道横截面面积之比

Φ——进气道入口处的水力直径，m

目前较为普遍接受的St与Re经验关系式为[15]

(4)

2.2 压电悬臂梁复合结构的受迫振动

压电悬臂梁复合结构在来流作用下产生横向振动自发电模型如图4所示。该结构包括弹性装载的绕流圆柱、压电悬臂梁和相应的负载电阻电路，由牛顿第二定律对该复合结构进行受力分析得[16]

图4 压电悬臂梁复合结构自发电模型Fig.4 Self-generation model of composite structure of piezoelectric cantilever beam

(5)

(6)

其中

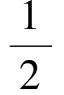
(7)

式中M——圆柱单元长度的质量，kg

Y——圆柱轴线沿Y轴方向的位移，m

C——结构阻尼常数

K——结构刚度常数

Θ——系统机电耦合项，N/V

Cp——压电材料的电容，F

R——负载电阻，Ω

U——负载电阻的电压，V

穿过大门，就来到了王宫的内庭。整座王宫大致呈“回”字形，在中间围成一个方正的庭院，庭院正中是一座灯塔，石头做成的灯柱上有两盏明灯，还有很多金色的装饰。

FL(t)——圆柱不同时刻在Y轴方向上所受的升力，N

CL——升力系数

A——圆柱在垂直于来流方向上的迎流投影面积，m2

为了计算压电悬臂梁复合结构的一阶横向振动频率，选用圆柱直径D和流场特征速度v作为长度和速度尺度，式(5)～(7)可简写为

(8)

(9)

其中

Y*=Y/D

(10)

v*=v/(fND)

(11)

(12)

m*=4m/(ρπD2)

(13)

(14)

(15)

式中Y*——圆柱无量纲沿Y轴方向的位移

v*——约化速度，m/s

ξ——结构阻尼比率m*——质量比

U*——无量纲电压

p——流体压力，Pa

ωv——圆柱表面的翼展涡度分量

θ——面积分量的外法线与流动方向所成的角度，rad

fN——压电悬臂梁复合结构一阶横向振动频率，Hz

由于固定于压电悬臂梁复合结构末端的圆柱不发生变形，设压电悬臂梁复合结构的绝对横向位移为u(x，t)，根据达朗贝尔原理[17]，视为刚体的圆柱在振动过程中可等效为惯性力Fg和惯性力矩Mg，计算公式为[18]

(16)

(17)

式中L2——压电材料长度，m

L——金属基板长度，m

J——圆柱对其重心的转动惯量，kg·m2

由此可得到装载圆柱的压电悬臂梁复合结构的频率特征方程和振动方程分别为

(18)

(19)

其中

ω=2π/fN

(20)

式中ρ1——压电悬臂梁密度，kg/m3

A1——压电悬臂梁横截面积，m2

E——压电悬臂梁弹性模量，Pa

ω——压电悬臂梁复合结构固有角频率，rad/s

联立式(18)～(20)，可求得fN。

综上可求得三阶常微分方程耦合系统方程为

(21)

(22)

(23)

其中

3 流场数值分析

由于流体在绕流圆柱和压电悬臂梁复合结构的共同作用下呈现为湍流，运动形态复杂且难于直接观察，因此本文利用计算流体动力学软件Fluent对涡激振动自发电装置的内部流场进行分析，以明确系统的结构参数。

由于亥姆霍兹共振器的共振频率仅与自身结构参数有关[19]，为简化计算过程，本文先使得卡门涡街的脱涡频率、压电悬臂梁复合结构的一阶横向振动频率相等后，再通过设定亥姆霍兹共振器的结构尺寸使3个频率达到一致。

3.1 腔体流场设置

赵静等[20]研究表明，当在Re=1 000的条件下，单圆柱尾流侧增设横隔板时，斯特劳哈尔数St减小，进而引起脱涡频率发生改变，导致升力幅值增加，并增大压电悬臂梁的摆动幅度。段志强[21]进一步探讨在Re=200的条件下，三维圆柱层流模型和不同楔形板长对绕流流场、斯特劳哈尔数St和升阻力系数的影响，结果表明，当板长与圆柱直径之比等于2.5时，升力系数幅值出现极大值。KWON等[22]研究结果表明，板长对流场特性的影响与雷诺数有关。梁亮文[23]研究表明，当圆柱的摆动频率与其自身脱涡频率相近时，尾流沿圆柱高度方向的流动会被圆柱抑制，使得流场在较大的雷诺数范围内没有明显的三维特性。由于升力系数均方根在阻流比为0.2时达到最大[24]，为使亥姆霍兹共振器的脉冲射流能对圆柱产生作用，以圆柱直径D为基准尺度，设置腔体有限流道内流场计算域的范围为5D45D，圆柱中心距离流场入口和出口分别为5D和40D，两侧壁面距离圆柱中心均为2.5D，最终在计算流体力学软件Fluent中所建立的腔体二维流场域模型如图5所示。

图5 腔体二维流场域模型Fig.5 Two-dimensional flow field model of cavity

3.2 单圆柱绕流数值分析

为验证流场计算结果的准确性，先对Re=200时的单圆柱绕流进行数值模拟。数值计算时的边界条件如下：

(1)模型入口和出口分别设置为速度入口(Velocity inlet)和压力出口(Pressure outlet)，其中入口处的速度为0.292 m/s，出口绝对压力为1.01×10-5Pa，环境温度为25℃，整个流场为等温单相流模型。

(2)数值计算时工作流体为理想空气，密度为1.225 kg/m3，动力粘性系数μ为1.789 4×10-5Pa·s。

(3)整个流场计算域基于纳维-斯托克斯方程(Navier-Stokes equations，N-S方程)，并使用大涡模拟(Large eddy simulations，LES)湍流模型进行求解。为准确捕捉腔体有限流道内的流场动力学特性，设定流场计算域的基本单元尺寸设置为1 mm，并对圆柱周面及两侧壁面进行12级细化处理，采用混合网格对整个计算域进行划分，最终得到计算域的单元数为34 554，节点数为35 071。

(4)为使卡门涡街的瞬态动力学行为精细化，将流场域求解时间步长设为涡旋脱落周期的1/20。

图6为单圆柱绕流的涡量图。从图6可以看出，气体流动在圆柱后面发生分离，并在圆柱尾部附近形成一定频率的卡门涡街。图7为单圆柱绕流的升阻力系数随流动时间变化的关系曲线。从图7可看出，升阻力系数均呈现周期性的变化，并且阻力系数的变化频率为升力系数的两倍，这一规律与JIANG等[25]研究结果一致。

图6 单圆柱绕流的涡量云图Fig.6 Vorticity cloud of single cylinder

图7 单圆柱绕流的升阻力系数随时间的变化曲线Fig.7 Variation curves of lift-resistance coefficient of single cylinder

通过对图7中单圆柱绕流的升力系数曲线进行快速傅里叶变换，得到该条件下单圆柱绕流脱涡频率f=7.14 Hz，利用式(2)和式(3)求得此时的斯特劳哈尔数为0.183，与经验式(4)的相对误差为7.1%。

3.3 不同板长对流场特性的影响

为研究流场中压电悬臂梁复合结构柔性金属基板的板长L对斯特劳哈尔数St和升阻力系数的影响，基于单圆柱绕流流场设置对腔体流场进行仿真分析。由于固定和自由边界条件下长短悬臂梁的脱涡频率不变[26]，本文将忽略流体与固体之间的交互作用对脱涡频率的影响。根据江滢等[27]的研究结果，为适应沿海地区夏季近地层自然风速，将流场入口来流速度设为5 m/s，在此条件下雷诺数Re为3 424。

图8为绕流圆柱后方附加不同板长条件下，内流场的涡量云图。从图8可以看出，圆柱后附加的压电悬臂梁复合结构明显影响了边界层的气流分离，使得涡旋脱落的起点沿流动方向下移。而且随压电悬臂梁复合结构长度L的增加，边界层气流分离的起始点距离圆柱也越远，同时涡间距离变大。

图8 不同板长条件下流场涡量云图Fig.8 Vorticity clouds of flow field under different plate length conditions

图9为升力、阻力系数和脱涡频率随板长L变化的关系曲线。从图9可以看出，当L/D=2时，升力系数幅值出现最大值为1.3。这表明在此条件下，压电悬臂梁复合结构的振幅最大。此后，随着板长L的增加，升力、阻力系数均呈减小趋势。此外，图9还表明，脱涡频率f并非定值，其随板长L的增大而减小，在L/D=1取得最大值为130 Hz。显然，带压电悬臂梁复合结构的圆柱体流场的斯特劳哈尔数St与板长L为非线性的关系。

图9 流场参数随板长的变化曲线Fig.9 Variation curves of flow field parameter with board length

4压电悬臂梁复合结构横向振动频率随板长变化规律

为使压电悬臂梁复合结构的横向振动频率与流场中的脱涡频率一致，利用有限元软件ANSYS的动力学和压电分析模块，对压电悬臂梁进行模态分析，以求得到不同板长条件下压电悬臂梁复合结构的一阶横向振动频率。考虑悬臂梁复合结构在工作时须做往复运动[28]，因此分别选用紫铜和聚偏氟乙烯(Polyvinylidene fluoride，PVDF)压电薄膜作为柔性金属基体和柔性压电体的材料； ABS工程塑料(Acrylonitrile-butadiene-styrene copolymer)作为绕流圆柱的材料。材料参数如表1所示。

表1 材料参数Tab.1 Parameters of materials

图10为压电悬臂梁复合结构长度L/D=3时一阶横向振动模态振型图。此时，复合结构的一阶横向振动频率为61.085 Hz。图11为压电悬臂梁复合结构一阶横向振动频率和脱涡频率随板长L变化的关系曲线。由图11可知，复合结构的横向振动频率随板长L的增加而减小，当L/D=1.8时，压电悬臂梁复合结构的一阶横向振动频率与该条件下流场脱涡频率一致，为113 Hz。在此条件下，压电悬臂梁复合结构受流场涡激力作用产生共振，使其横向振动的振幅增大。

图10 压电悬臂梁复合结构一阶横向振动模态振型图(L/D=3)Fig.10 First-order transverse vibration mode of composite structure of piezoelectric cantilever beam(L/D=3)

图11 压电悬臂梁复合结构的一阶横向振动频率和脱涡频率随板长L的变化曲线Fig.11 Variation curves of first-order transverse vibration and frequency of composite structure of piezoelectric cantilever beam with board length L

5 亥姆霍兹共振器结构优化设计

亥姆霍兹共振器由一个带开口颈部短管的空腔构成。它受外界声场的激发引起空腔气体的振动，同时空腔内的振动又通过短管发出声波加强外界的声场，因此可将其等效为弹簧-质量系统，颈部短管气体体积和空腔气体体积分别等效为质量块和弹簧，其结构示意图如图12所示。共振器内气体振动的频率为[29]

(24)

其中

V=π(d′/2)2l′

(25)

L1=l+0.85d

(26)

式中fHR——亥姆霍兹共振器的谐振频率，Hz

C1——大气声速，25℃条件下为346 m/s

S——颈部短管截面面积，m2

V——容腔容积，m3

d′——容腔底部直径，m

l′——容腔高度，m

L1——颈部短管的有效长度，m

l——短管长度，m

d——短管直径，m

图12 亥姆霍兹共振器和弹簧-质量系统Fig.12 Helmholtz resonator and spring-quality system1.外界声场 2.反射声场 3.颈部短管 4.容腔 5.弹簧 6.质量块 7.压力

此外，声场放大比率G的表达式为[30-31]

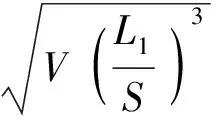
(27)

高虹[11]研究表明，当外界气流压力扰动的频率是亥姆霍兹共振器的整数倍时，共振器空腔内可以产生自激振荡脉冲射流。因此，本节的优化目标是使声场放大比率G达到最大，同时共振器谐振频率与压电悬臂梁复合结构的横向振动频率一致。考虑到压电悬臂梁复合结构的实际尺寸，故共振器优化设计的数学模型可表述为

(28)

式中：d′、d、l′、l均为设计变量。利用罚函数法[32]，经优化计算后可得到亥姆霍兹共振器的几何尺寸如表2所示，此时声场放大比率G=1 225.82。

表2 亥姆霍兹共振器的几何尺寸Tab.2 Geometric dimensions of Helmholtzresonator m

为了提高声场放大功效，本文采用亥姆霍兹共振器组对称布置的方式(图1)，当脉冲射流从一侧的共振器喷出，推动压电悬臂梁复合结构从中部开始产生向另一侧的横向振动，同时另一侧的共振器处于气体吸入阶段，其出口处产生负压从而拉动压电悬臂梁复合结构继续向该侧摆动。当共振器组的脉冲射流进程和吸气进程结束时，压电悬臂梁复合结构达到振幅最大，随后在结构本身弹性力的作用下，向另一侧摆动。由于共振器的谐振频率与压电悬臂梁复合结构的横向振动频率一致，因此，这一过程将循环往复。

图13 不同时刻自发电装置流场压力云图Fig.13 Flow field pressure clouds of self-generating device at different times1.圆柱 2.压电悬臂梁复合结构 3.1号亥姆霍兹共振器 4.2号亥姆霍兹共振器 5、6.涡旋

图13为一个周期内，自发电装置流场在4个典型时刻的压力云图。从图13可以看出，在圆柱和压电悬臂梁复合结构后部均出现涡旋脱落。其中，在T/4和3T/4时刻(图13a)，2个亥姆霍兹共振器内压强相等，此时圆柱处在腔体中部平衡位置；在T/2时刻(图13b)，涡旋从压电悬臂梁复合结构的下端部脱落，此时圆柱受到流场升力作用横向振动到腔体下侧，同时1号亥姆霍兹共振器的压强变大，处于脉冲射流进程，推动圆柱远离平衡位置，而2号亥姆霍兹共振器内为负压，处于吸气进程。同理，在T时刻(图13c)，1号亥姆霍兹共振器处于吸气进程而2号亥姆霍兹共振器处于脉冲射流进程。

为明确自发电装置内流场的压强变化规律，在流场内设置了4个监测点A、B、C和D(图13a)，图14为4个监测点的压力随时间变化曲线。由图14可知，同一共振器容腔内部的压力始终大于颈部短管处压力。同时，2个共振器不停在正压—脉冲射流、负压—吸气这2个进程之间有规律变换，且同时到达极限值，这种流场压力的变化规律验证了设计的合理性。

图14 4个监测点处压力的时间历程图Fig.14 Time history of pressure at four monitoring points

6 试验

为验证涡激振动自发电装置的自发电能力和振动特性，根据上述的理论结果，采用相同材料加工的试验样机如图15所示。其中，柔性金属基体和柔性压电体厚度均为0.1 mm。

图15 自发电装置试验样机Fig.15 Test prototype of self-generating device1.腔体 2.绕流圆柱 3.压电悬臂梁复合结构 4.基座 5.亥姆霍兹共振器

6.1 自发电能力试验测试

自发电测试的试验装置如图16所示，主要由可调速鼓风机(CZR型，上海沈业节能设备有限公司)、智能风速风压风量仪(YC-2000A型，龙岩亚成仪器仪表有限公司)、数字示波器(GDS-2004A型，苏州固纬电子有限公司)、小型升降台(OMY-200型，北京柠檬科技有限公司)、压电薄膜(PVDF-100型，锦州科信电子材料有限公司)等组成。

图16 自发电能力测量试验实物装置Fig.16 Physical device of self-generating capacity measurement test1.可调速鼓风机 2.涡激振动自发电装置 3.小型升降台 4.数字示波器 5.智能风速风压风量仪

气流从涡激振动自发电装置的入口处流入，流速可通过鼓风机进行调节，并且由智能风速风压风量仪读取。用风速风压风量仪在入口处测量3次，取平均值作为入口风速的测量值。气流通过绕流圆柱后产生涡旋，而涡旋的脱落又使得绕流圆柱和压电悬臂梁复合结构产生往复式横向振动，由此产生的电压幅值通过数字示波器记录。图17为自发电装置在5 m/s的风速下产生的理论与试验电压波形，试验测得最大输出电压幅值为6.0 V。

图17 自发电装置的理论与试验电压幅值Fig.17 Theoretical and experimental voltage waveforms of self-generating device

6.2 锁定风速区间测量试验

当圆柱后方涡旋脱落的频率接近于自身横向振动的固有频率时，脱涡频率会被锁定在固有频率上，圆柱振幅会显著增大但振动频率保持不变，当外界风速改变时，脱涡频率不受影响，这就是锁定现象[33]。为了确定该装置的锁定范围，通过测量不同风速条件下样机的发电能力，以求得锁定风速区间。

图18为自发电装置在不同入口风速条件下产生的电压幅值。从图18可看出，当入口风速在4～6.25 m/s区间内时，自发电装置的脱涡频率被锁定，且能产生输出较大的电压幅值，说明该装置对近地层不同风速的适应能力较强。为获得锁定区间内的脱涡频率，将智能风速风压风量仪的皮托管探头前端置于距离该装置内部的基座5 cm处，测量该点实际压力随时间的变化情况，并通过对其进行快速傅里叶变换，得到此时的脱涡频率为116 Hz。

6.3 振动特性测量试验

为确定绕流圆柱和压电悬臂梁复合结构的横向振动频率，利用激光测振仪(LV-S01型，舜宇光学科技有限公司)对绕流圆柱的横向振动振幅进行测量，所搭建的测量装置如图19所示。

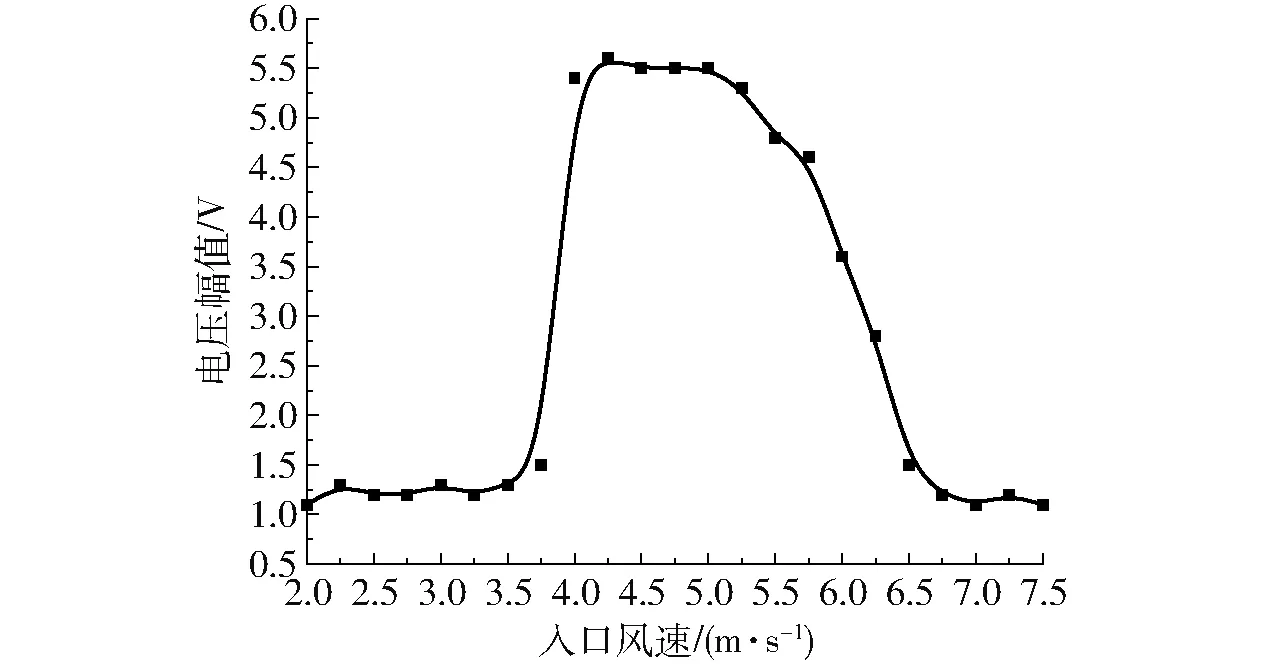
图18 自发电装置在不同风速下产生的电压幅值Fig.18 Voltage magnitude generated by self-generating device at different wind speeds

图19 振幅测量试验实物装置Fig.19 Physical device of amplitude measurement test1.激光测振仪控制器 2.可调速鼓风机 3.涡激振动自发电装置 4.计算机 5.小型升降台 6.激光测振仪光学头

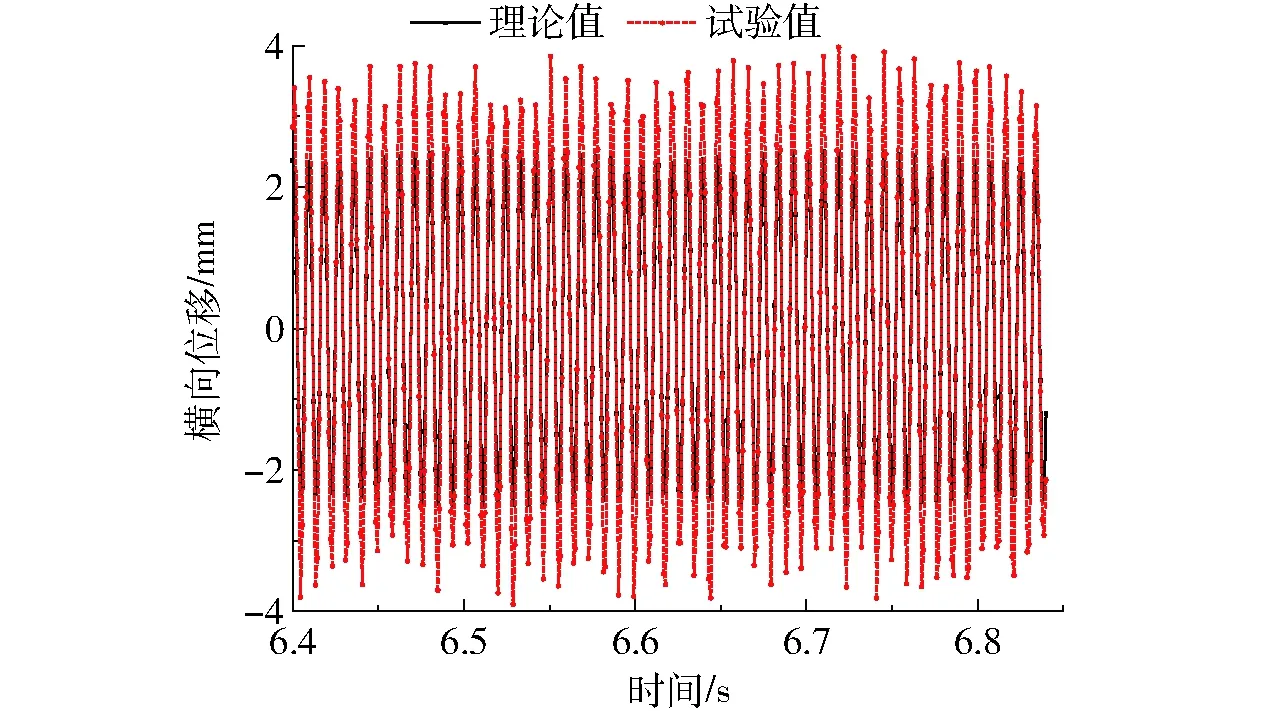
图20 绕流圆柱在风速为5 m/s时的振幅Fig.20 Amplitude of cylinder at speed of 5 m/s

图20为绕流圆柱在入口风速为5 m/s条件下的理论与试验振幅，由图20可以看出，绕流圆柱受涡旋脱落的影响，产生周期性的往复式摆动，其最大振幅可达到7.6 mm。图21为对该曲线进行快速傅里叶变换后的频谱图，可得到绕流圆柱的实际摆动频率为110 Hz。试验结果表明，在外界气流的冲击下，亥姆霍兹共振器产生谐振，绕流圆柱和压电悬臂梁复合结构发生横向振动，使得柔性压电体产生稳定的电压，且摆动频率与亥姆霍兹共振器的固有频率一致，数值计算结果与试验较为吻合。

图21 绕流圆柱振幅的频谱图Fig.21 Spectrum of amplitude of cylinder

7 结论

(1)基于Fluent的数值分析结果表明，绕流圆柱后方附加的压电悬臂梁复合结构明显影响了边界层的气流分离。在相同风速下，脱涡频率f和升力、阻力系数均随板长L的变化而改变。其中，随着板长L的增加，阻力系数幅值呈减小趋势，而升力系数幅值呈先急剧减小，随后缓慢增加，再逐步减小的趋势。当L/D=2时，升力系数幅值出现极大值1.3，此时压电悬臂梁复合结构的振幅最大。

(2)在5 m/s的风速下，绕流圆柱的振动频率为110 Hz，且流场的涡脱频率、压电悬臂梁复合结构摆动频率与亥姆霍兹共振器的谐振频率一致，数值计算结果与试验较为吻合。

(3)自发电装置在5 m/s的风速下可产生两相稳定的开路电压，并且测得最大输出电压幅值为6.0 V，最大振幅可达到7.6 mm。当入口处风速范围在4～6.25 m/s时，为该自发电装置的自锁风速区间，在此风速范围内，自发电装置均能产生较大的电压。

1 葛文杰，赵春江.农业物联网研究与应用现状及发展对策研究[J/OL]. 农业机械学报，2014，45(7)：222-230.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1amp;file_no=20140735amp;journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2014.07.035.

GE Wenjie, ZHAO Chunjiang. State-of-the-art and developing strategies of agricultural internet of things[J]. Transactions of the Chinese Society for Agricultural Machinery, 2014,45(7):222-230. (in Chinese)

2 罗锡文, 臧英, 周志艳. 精细农业中农情信息采集技术的研究进展[J]. 农业工程学报, 2006, 22(1):167-173.

LUO Xiwen, ZANG Ying, ZHOU Zhiyan.Research progress in farming information acquisition technique for precision agriculture[J]. Transactions of the CSAE, 2006, 22(1):167-173.(in Chinese)

3 SHAIKH F K, ZEADALLY S. Energy harvesting in wireless sensor networks: a comprehensive review[J]. Renewable and Sustainable Energy Reviews, 2016, 55:1041-1054.

4 YUAN F, JIN S, WONG K K, et al. Wireless information and power transfer design for energy cooperation distributed antenna systems[J]. IEEE Access, 2017, 5: 8094-8105.

5 LU X, WANG P, NIYATO D, et al. Wireless networks with RF energy harvesting: a contemporary survey[J]. IEEE Communications Surveys amp; Tutorials, 2015, 17(2): 757-789.

6 MA S, YANG Y, QIAN Y. Energy harvesting for wireless sensor networks: applications and challenges in smart grid[J]. International Journal of Sensor Networks, 2016, 21(4):226-241.

7 赵勇, 韩斌, 房刚利. 风力发电机状态监测与故障诊断技术综述[J]. 热力发电, 2016, 45(10):1-5.

ZHAO Yong, HAN Bin, FANG Gangli.A survey of condition monitoring and fault diagnosis for wind power generators[J]. Thermal Power Generation, 2016, 45(10):1-5.(in Chinese)

8 程廷海, 王英廷, 付贤鹏, 等. 定质量分数交变气体载荷激励下压电阵列发电机实验[J/OL]. 农业机械学报, 2017, 48(2):407-412.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1amp;file_no=20170255amp;journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2017.02.055.

CHENG Tinghai, WANG Yingting, FU Xianpeng, et al. Experiment on piezoelectric plate array energy harvester excited by alternate high air pressure with constantly gaseous mass[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2017, 48(2):407-412. (in Chinese)

9 BOWEN C R, KIM H A, WEAVER P M, et al. Piezoelectric and ferroelectric materials and structures for energy harvesting applications[J]. Energy amp; Environmental Science, 2014, 7(1): 25-44.

10 HEIL M, ROSSO J, HAZEL A. Topological fluid mechanics of the formation of the Kármán-vortex street[J]. Journal of Fluid Mechanics, 2017, 812:199-221.

11 高虹. Helmholtz共振的机理研究及应用[D]. 重庆：重庆大学, 2003.

GAO Hong. Mechanism of Helmholtz oscillator and its application[D]. Chongqing: University of Chongqing, 2003.(in Chinese)

12 白桦, 李加武, 夏勇. 低雷诺数圆柱绕流数值模拟及控制措施[J]. 建筑科学与工程学报, 2010, 27(4):39-43.

BAI Hua, LI Jiawu, XIA Yong. Numerical simulation and control measures of flow around circular cylinders at low Reynolds number[J]. Journal of Architecture and Civil Engineering, 2010, 27(4):39-43.(in Chinese)

13 XU F, CHEN W L, BAI W F, et al. Flow control of the wake vortex street of a circular cylinder by using a traveling wave wall at low Reynolds[J]. Computers amp; Fluids, 2017, 145:52-67.

14 文晟, 张铁民, 杨秀丽, 等. 涡致振动型风力压电俘能器流场数值模拟与试验[J/OL]. 农业机械学报, 2014, 45(2):269-275.http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1amp;file_no=20140245amp;journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2014.02.045.

WEN Sheng, ZHANG Tiemin, YANG Xiuli, et al. Numerical simulation and experiment of a wind piezoelectric energy harvester based on vortex-induced vibrations[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2014, 45(2):269-275.(in Chinese)

15 BOUZARI S, GHAZANFARIAN J. Unsteady forced convection over cylinder with radial fins in cross flow[J]. Applied Thermal Engineering, 2016, 112:214-225.

16 MEHMOOD A, ABDELKEFI A, HAJJ M R, et al. Piezoelectric energy harvesting from vortex-induced vibrations of circular cylinder[J]. Journal of Sound and Vibration, 2013, 332(19):4656-4667.

17 鹿玲, 姚建涛, 顾伟栋, 等. 基于Kane方程的冗余驱动5UPS/PRPU并联机床动力学分析[J/OL]. 农业机械学报, 2016, 47(6): 366-372. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1amp;file_no=20160648amp;journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2016.06.048.

LU Ling, YAO Jiantao, GU Weidong, et al. Dynamics analysis of 5UPS/PRPU parallel machine tool with redundant actuation based on Kane equation[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2016, 47(6):366-372. (in Chinese)

18 张淼, 孟庆丰, 王宏金. 考虑疲劳寿命的压电悬臂梁结构优化设计方法[J]. 压电与声光, 2015, 37(1):68-72.

ZHANG Miao, MENG Qingfeng, WANG Hongjin.Structure optimization design method for piezoelectric cantilever beam considering fatigue life[J]. Piezoelectrics amp; Acoustooptics, 2015, 37(1):68-72.(in Chinese)

19 PILLAI M A, EZHILARASI D. Improved acoustic energy harvester using tapered neck Helmholtz resonator and piezoelectric cantilever undergoing concurrent bending and twisting [J]. Procedia Engineering, 2016, 144:674-681.

20 赵静, 潘树春, 吕林, 等. 带横隔板圆柱绕流的三步有限元大涡模拟[J]. 中国海上油气, 2009, 21(5):347-351.

ZHAO Jing, PAN Shuchun, LÜ Lin, et al. Large eddy simulation of flow past a circular cylinder with splitter plate based on three-step finite element method[J]. China Offshore Oil and Gas, 2009, 21(5):347-351.(in Chinese)

21 段志强. 低雷诺数下尾部隔板影响圆柱绕流的数值研究[D]. 重庆：重庆大学, 2012.

DUAN Zhiqiang. An numerical investigation on fluid flow past a circular cylinder with splitter plate at low Reynolds number[D]. Chongqing: University of Chongqing, 2012.(in Chinese)

22 KWON K, CHOI H. Control of laminar vortex shedding behind a circular cylinder using splitter plates[J]. Physics of Fluids, 1996, 8(2):479-486.

23 梁亮文. 低雷诺数下圆柱横向受迫振荡和涡激运动的数值分析[D]. 上海：上海交通大学, 2009.

LIANG Liangwen. Numerical analysis of forced oscillation and vortex-induced motion of circular cylinder in cross flow with low Reynolds number[D]. Shanghai: Shanghai Jiao Tong University, 2009.(in Chinese)

24 蒋赟. 阻流比与长径比对低雷诺数圆柱绕流尾迹演化的影响研究[D]. 长沙：中南大学, 2014.

JIANG Yun. The effect of blockage ratio and aspect ration on the evolution of circular cylinder wake at low Reynolds numbers[D]. Changsha: Central South Univesity,2014.(in Chinese)

25 JIANG X, ANDREOPOULOS Y, LEE T, et al. Numerical investigations on the vortex-induced vibration of moving square cylinder by using incompressible lattice Boltzmann method[J]. Computers amp; Fluids, 2016, 124:270-277.

26 EVANGELINOS C, LUCOR D, KARNIADAKIS G. DNS-derived force distribution on flexible cylinders subject to vortex-induced[J]. Journal of Fluids and Structures, 2000, 14(3):429-440.

27 江滢, 赵宗慈. 中国沿海地区夏季风速时空变化特征和气候模式结果评估与预估分析[J]. 科技导报, 2011, 29(6):21-30.

JIANG Ying, ZHAO Zongci. Characteristics of summer wind speed changes over coastal region of China[J]. Science amp; Technology Review, 2011, 29(6):21-30.(in Chinese)

28 黄健萌, 黄靖. 压电驱动微悬臂梁与基底粗糙面间多次接触分析[J/OL]. 农业机械学报, 2015, 46(9):368-372. http:∥www.j-csam.org/jcsam/ch/reader/view_abstract.aspx?flag=1amp;file_no=20150954amp;journal_id=jcsam. DOI: 10.6041/j.issn.1000-1298.2015.09.054.

HUANG Jianmeng, HUANG Jing. Multiple-contact analysis between microcantilever and substrate rough surface driven by piezoelectric[J/OL]. Transactions of the Chinese Society for Agricultural Machinery, 2015, 46(9):368-372. (in Chinese)

29 HOUSTON B, WANG J, QIN Q, et al. Experimental and numerical investigation of Helmholtz resonators and perforated liners as attenuation devices in industrial gas turbine combustors[J]. Fuel, 2015, 151:31-39.

30 NOH S, LEE H, CHOI B. A study on the acoustic energy harvesting with Helmholtz resonator and piezoelectric cantilevers[J]. International Journal of Precision Engineering and Manufacturing, 2013, 14(9):1629-1635.

31 NEMATI N, KUMAR A, LAFARGE D, et al. Nonlocal description of sound propagation through an array of Helmholtz resonators[J]. Comptes Rendus Mecanique, 2015, 343(12): 656-669.

32 张建桃, 李晟华, 文晟, 等. 农用超声雾化换能器参数优化设计与试验[J]. 农业工程学报, 2015, 31(12):8-15.

ZHANG Jiantao, LI Shenghua, WEN Sheng, et al.Parameter optimization design and experiment of agricultural ultrasonic atomization transducer[J]. Transactions of the CSAE, 2015, 31(12):8-15.(in Chinese)

33 WANG J, WEN S, ZHAO X, et al. Piezoelectric wind energy harvesting from self-excited vibration of square cylinder[J]. Journal of Sensors, 2016:1-13.

DesignandExperimentofVortex-inducedVibrationSelf-generatingDeviceBasedonPrincipleofResonantAcousticAmplification

WEN Sheng1,2LI Shenghua2,3ZHANG Jiantao2,4LAN Yubin2,3ZHANG Haiyan2,3XING Hang2,3

(1.EngineeringFundamentalTeachingandTrainingCenter,SouthChinaAgriculturalUniversity,Guangzhou510642,China2.NationalCenterforInternationalCollaborationResearchonPrecisionAgriculturalAviationPesticidesSprayingTechnology,Guangzhou510642,China3.CollegeofEngineering,SouthChinaAgriculturalUniversity,Guangzhou510642,China4.CollegeofMathematicsandInformatics,SouthChinaAgriculturalUniversity,Guangzhou510642,China)

In order to acquire clean energy from the natural environment and supply power to the wireless sensors and communication modules, a vortex-induced vibration self-generating device was designed based on the principle of vortex-induced vibration and resonant acoustic amplification. The device mainly consisted of a cavity, a cylinder, a piezoelectric cantilever composite structure, a base and two Helmholtz resonators. Firstly, mechanical analysis of the piezoelectric cantilever composite structure in the self-generating device was carried out. Secondly, based on the computational fluid dynamics method, the dynamic characteristics of the flow field of self-generating device under different plate lengths were analyzed. And the influence of length of cantilever beam on vortex frequency, lift and drag coefficient was clarified. The finite element software ANSYS was used to simulate the transverse reciprocating vibration of piezoelectric cantilever composite structure to finish the structural design. Finally, the structural dimensions of the Helmholtz resonator on both sides of the device were optimized to make the flow field vortex shedding frequency. And the first-order transverse vibration frequency of piezoelectric cantilever composite structure and the resonant frequency of the resonator was consistent. The experimental results demonstrated that the self-generating device can produce an open-circuit voltage with a peak-to-phase voltage of 6.0 V at wind speed of 5 m/s, and the above three frequencies were consistent. The experimental results also showed that the speed of 4～6.25 m/s was the self-locking wind speed range of the self-generating device. Within the wind speed range, the self-generating device can produce the maximum voltage amplitude. The results of the study provided a reference for the structural design of the vortex-induced vibration self-generating device.

vortex-induced vibration; flow field analysis; piezoelectric power generation; resonance; acoustic amplification

10.6041/j.issn.1000-1298.2017.11.025

TN384

A

1000-1298(2017)11-0204-11

2017-08-23

2017-09-08

国家重点研发计划项目(2016YFD0200700)、广东省自然科学基金项目(2015A030310182)和广东省科技计划项目(2016A020210092、2016A020210100)

文晟(1974—)，男，副教授，主要从事压电振动和精准农业研究，E-mail: vincen@scau.edu.cn

张建桃(1978—)，男，副教授，主要从事精细农业和压电器件研究，E-mail: zhangjiantao@yeah.net